基于时间Petri网的综合航电系统时序验证分析

， ，

(南昌航空大学软件学院，南昌 330063)

基于时间Petri网的综合航电系统时序验证分析

樊鑫，郑巍，梁旗军

(南昌航空大学软件学院，南昌330063)

综合航电系统是一种对可靠性、实时性要求非常高的嵌入式应用系统;为了解决针对复杂应用场景下综合航电系统的处理时间和工作时序预估较困难、且计算自动化程度不高等测试验证问题，提出了一种基于时间约束Petri网的综合航电系统时序验证和分析方法;给出了时间约束Petri网的形式化定义，分析了综合航电系统工作流程中各节点的时间属性，通过引入时序约束路径的概念，并提出了时序推理算法;通过在仿真算例中进行计算并对比实际运行数据，结果表明该方法在针对综合航电系统运行时序的验证分析方面具有有效性。

综合航电系统；时间Petri网；时序约束路径；时序推理算法

0 引言

综合模块化航空电子(integrated modular avionics，IMA)是目前航空电子系统体系结构发展的最新阶段，在国内通常被称为综合航电系统。由于综合航电系统具有系统综合化且较之一般应用软件，绝大多数综合航电软件对实时性要求更高，需要能及时、正确响应外部发生的随机事件。这些特征给综合模块化航电系统的测试和验证带来了新的问题和挑战。国内外学者近年来开展了大量的研究，在仿真测试环境搭建[1-2]、模型驱动的测试验证方法[3-4]及系统建模[5]等方面均提出了相应的方法。文献[2]提出一种分布式仿真测试环境的软件体系结构设计，该结构应用代理模式，解决了分布式测试环境节点间实时通讯的关键技术，且该测试平台已成功地应用于多个航电软件的系统测试中。文献[3]和文献[4]分别选择SysML顺序图和活动图模型对航电嵌入式软件进行系统建模，并提出了集成测试和安全性测试方法。综合以上的研究工作，目前针对综合航电系统时间特性的验证方法研究较少，且UML或SysML模型本身在时间属性的表述能力方面相对欠缺，因此，如何能对综合航电系统的时间属性进行验证和分析是目前需要研究的重要课题。

Petri网能够对离散并行系统进行严密的数学表示，且物理意义清楚、推理过程简洁、易于自动化，在近年来受到越来越多的关注。为了使Petri网能够更好地描述系统的时间属性和系统可调度性，国内不少学者已经完成了很多前期的基础性研究，并扩展了Petri网模型的时间信息表达能力[6]，且在电力系统故障的预测和诊断领域得到了广泛地应用和实践[7-9]。文献[6]提出了时间Petri网的混合语义模型，并提出了状态类分析方法，用以模型的可调度性分析和时间计算。文献[7]利用电力系统故障过程中，警报信息中蕴含的时间信息，提出了一种时间溯因推理的电网智能诊断报警方法。文献[8]通过充分分析电网警报信息的时序属性和保护断路器动作的逻辑规则，提出了一种基于时间约束Petri网的电网警报处理及故障诊断方法。文献[9]针对诊断模型容错性不强的问题，提出了一种融合时序约束网络的模型Petri网故障诊断模型。

在综合航电系统的运行过程中，各子系统或各分区应用系统的处理活动也具有相应的时间属性。尤其在复杂应用场景下，由于子系统和各分区应用系统的数据交互增多且并发、转移活动也相应增加，给手工分析验证时间属性带来了较大困难。因此，分析综合航电系统中各交互活动的时间属性，并引入时间Petri网来对系统进行建模和仿真，对研究综合航电系统时间属性的验证方法具有重要的意义。

本文分析了综合航电系统中各交互活动的时序属性，并研究了存在的时间约束关系，通过引入时间Petri网(Timed Petri Net)，提出了一种基于时序约束路径的时序推理算法，该方法能够有效地计算综合航电系统工作流程中各节点的时间属性，为系统验证分析提供了有效的解决方法。

1 时间Petri网

1.1 时间约束定义

时间约束是为更好地描述时间属性而定义的用于约束相应时间属性的范围信息，主要包含时间点约束和时间段约束。

1)时间点约束。

时间点约束定义为时间区间T(t)=[t,t+]，用以描述事件发生时间t的不确定性，即事件发生的确切时间t属于约束范围T(t)，t∈T(t)。

2)时间长度约束。

时间长度是两个时间点之间的时间跨度。用δ(ti,tj)表示时间点ti和tj之间的时间跨度，即δ(ti,tj)=tj-ti。时间长度约束定义为Δ(ti,tj) =[Δtij,Δtij+],表示时间长度δ(ti,tj)的约束范围，即δ(ti,tj)∈Δ(ti,tj)，且Δtij和Δtij+分别表示时间段δ(ti,tj)的最小取值和最大取值。

1.2 TPN形式化描述

根据Petri网的定义，并考虑事件的时序属性，将TPN定义为六元组：

TPN= {P,T,I,O,F,δ}

其中：P={p1,p2,…,pn}，为库所的有限集合；T={t1,t2,…,tn}，为变迁的有限集合；I：T→P为从变迁到所有库所得输入映射函数；O：T→P为从变迁到所有库所得输出映射函数；F?(T×P) ∪(P×T)为库所和变迁之间所有关联弧的集合；δ={δ1,δ2,…,δn}为对应所有变迁的时间约束条件集合。

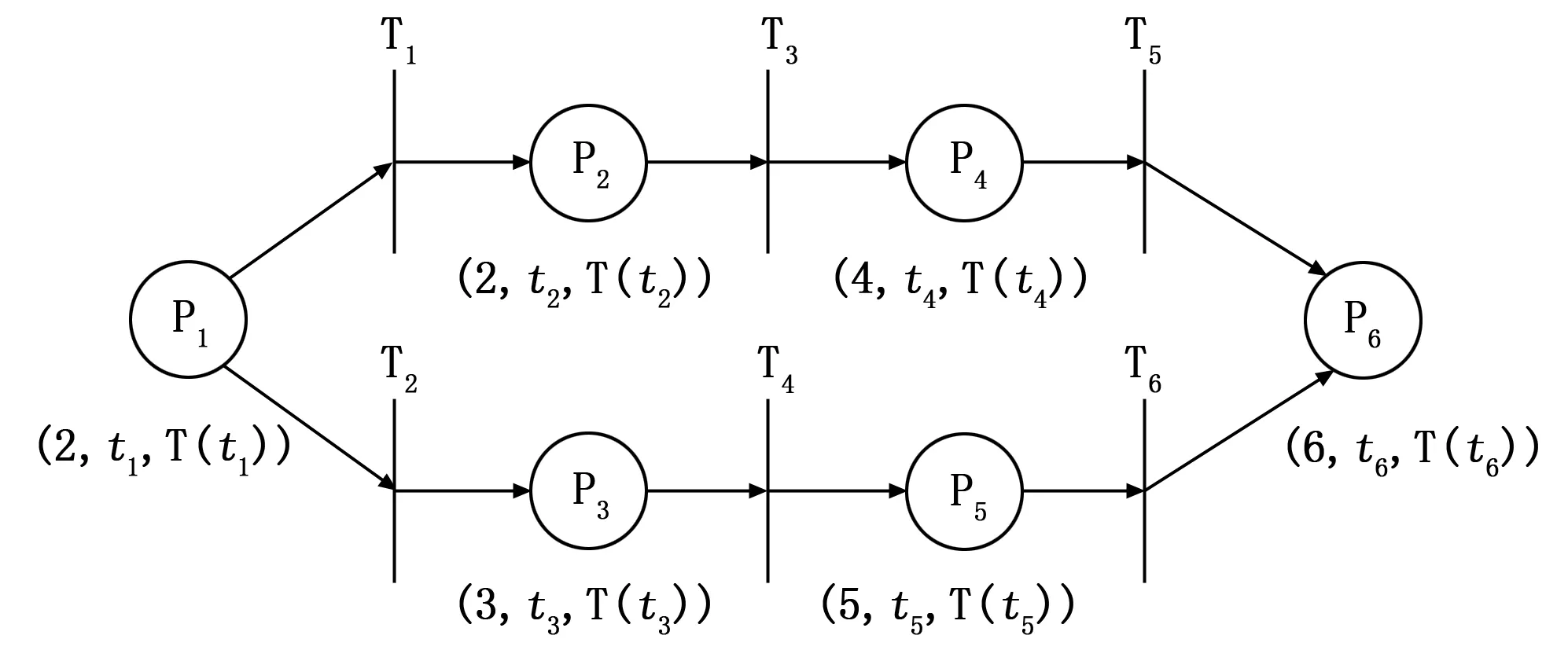
图1 一个简单的TPN

为了方便后续的讨论，假设pi和tk为TPN中的某个库所和变迁，则定义tk的最近前驱库所集合NPre(tk)、前驱库所集合Pre(tk)、最近后继库所集合NPost(tk)以及后继库所集合Post(tk)如下：

1)如果存在从库所pi到达变迁tk的弧，则称pi为变迁tk的前驱库所，变迁tk的所有前驱库所组成的集合即为变迁tk的前驱库所集合，记为集合Pre(tk)，将变迁tk最近的前驱库所构成的集合称为最近前驱库所集合NPre(tk)；

2)如果存在从变迁tk到达库所pi的弧，则称pi为变迁tk的后继库所，变迁tk的所有后继库所组成的集合即为变迁tk的后继库所集合，记为集合Post(tk)，将变迁tk最近的后继库所构成的集合称为最近后继库所集合NPost(tk)；

1.3 TPN时序推理基本规则

在本文中用Petri网的库所表示综合航电系统中的相应活动或事件。如果活动i的发生可以触发活动j的发生，则活动i为活动j的前驱，活动j为活动i的后继，可表示为i→j；反之，如果活动i发生了，则活动j不发生，则活动i为活动j的互斥活动，可表示为i?j。假设库所表示的活动为i,j,k,p,q在时间点ti,tj,tk,tp,tq发生，且活动关系为p→q，q→i，i→j，j→k。

1)前向时序推理规则

前向时序推理可推导出后继活动的时间约束，具体计算规则如下：

T(tj)=T(ti) +Δ(ti,tj) = [t+Δtij,t++Δtij+]

(1)

T(tk)=T(ti) +Δ(ti,tj) +Δ(tj,tk) =

[t+Δtij+Δtjk,t++Δtij++Δtjk+]

(2)

2)逆向时序推理规则

逆向时序推理可推导出前驱活动的时间约束，具体计算规则如下：

T(tq)=T(ti)-Δ(tq,ti)=[t-Δtqi,t+-Δtqi+] (3)

T(tp)=T(ti)-Δ(tq,ti)-Δ(tp,tq) =

[t-Δtqi-Δtpq,t+-Δtqi+-Δtpq+]

(4)

2 基于时间Petri网的综合航电系统时序验证算法

2.1 基于时间Petri网的时序验证流程

综合航电系统的时序验证以综合航电系统的工作场景为验证对象，采用时间Petri网模型对其进行时序验证主要是用于预测在某工作场景下航电系统整体处理时间的时间约束和预期的完成时间，其验证算法的流程如图2所示。

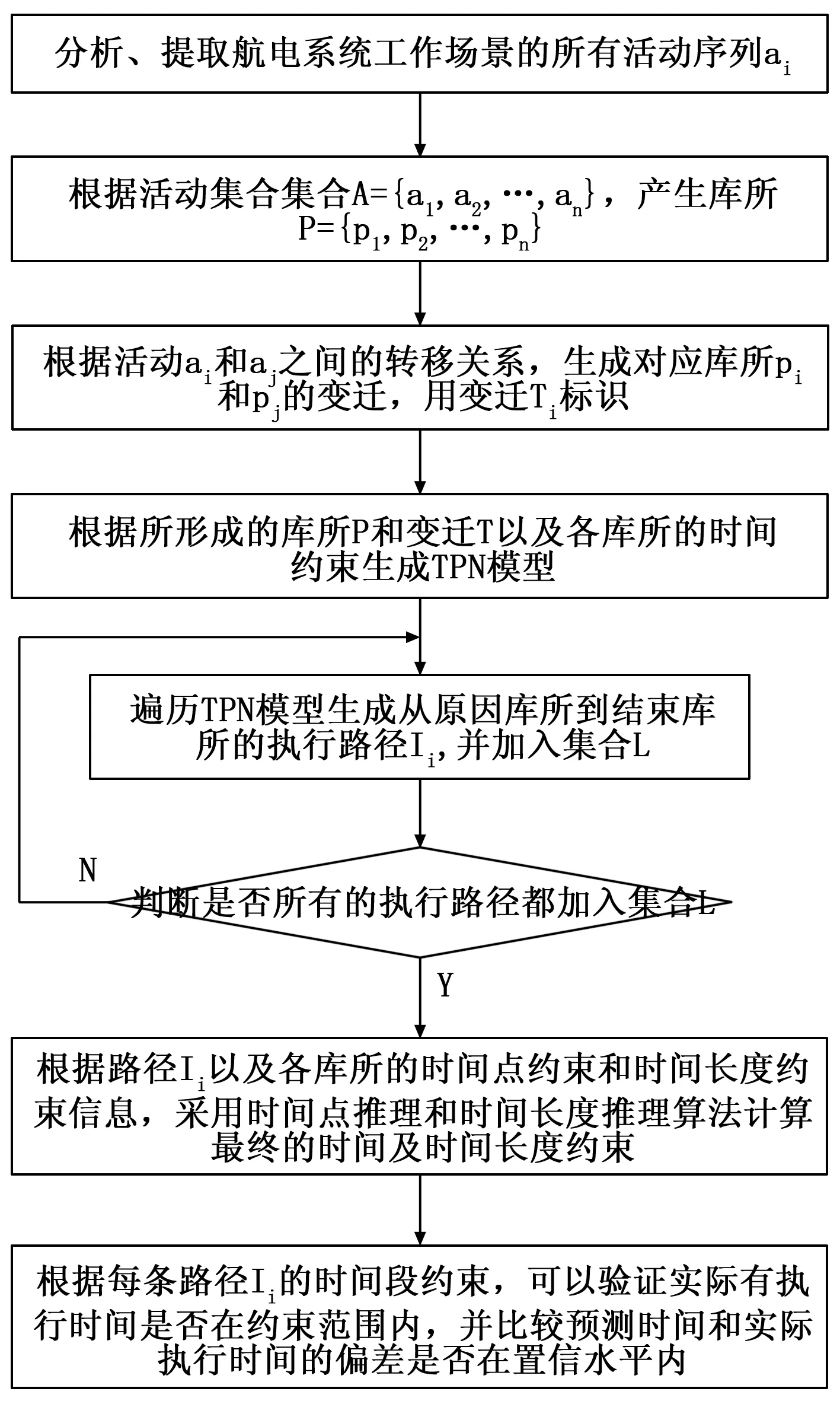
图2 时间Petri网的时序验证流程图

算法中相关集合的定义如下：

1)活动集合A。A={a1,a2,…,an}是航电系统某工作场景中全部活动ai的集合。

2)库所集合P。P={p1,p2,…,pn}是将航电系统某工作场景转换为TPN模型后的库所集合，在转换时工作场景中的活动ai可对应库所pi。

3)变迁集合T。T={t1,t2,…,tn}为将航电系统某工作场景转换为TPN模型后的变迁集合。变迁ti的定义如下：

?a1<.a2|a1,a2∈A→?ti|ti×p2∈I∧p1×ti∈O

其中，a1<.a2表示活动a2在活动a1执行后立即执行，且活动a1，a2在TPN中对应的库所为p1，p2。

4)路径集合L。L={l1,l2,…,ln}为在TPN中从原因库所到结束库所的库所序列组成的路径集合，li=。

2.2 基于时间Petri网的时间长度推理算法

基于时间Petri网的时间长度推理算法(TPN Time Distance Reasoning Algorithm， 简称TDRA算法)，是根据执行路径上的各库所的时间长度约束信息来推理最终执行完的时间长度约束的计算算法，其计算公式和方法如下：

1)假设计算路径为li=，即从pi开始到pm结束。

2)如果li=不存在并发活动所产生的库所，且迁移关系也没有并发关系，则计算方式为：

TL i= ∑{Δ(ti,tj),Δ(tj,tk), ...,Δ(tm’,tm) }

=Δ( ∑{Δtij,Δtjk,...Δtm’m},

∑{Δtij+,Δtjk+,...Δtm’m+})

(5)

3)如果li=存在并发活动所产生的库所，且迁移关系为并发关系，则计算方式为：

TL i=max{Δ(ti,tj),Δ(tj,tk), ...,Δ(tm’,tm) }

=Δ(max{Δtij,Δtjk,...Δtm’m},

max{Δtij+,Δtjk+,...Δtm’m+})

(6)

2.3 基于时间Petri网的时间点推理算法

基于时间Petri网的时间点推理算法(TPN Time Spot Reasoning Algorithm， 简称TSRA算法)，是根据执行路径上的各库所的时间长度约束信息来推理最终执行完的预估时间的计算算法，其计算公式和方法如下：

1)假设计算路径为li=，即从pi开始到pm结束。

2)在时间点推理算法中，需要为每个库所表示的事件或动作设置一个时间段占比参数drij，drij表示在δ(ti,tj)时间长度内pi通常会以何种比例的时间完成所对应的事件或动作，drij的取值可通过实际测试运行而统计得到。例如：若事件pi的时间长度约束为[20 ms,40 ms]，且其时段占比drij=50%，则可计算出实际所需的时间为20 + (40-20) ×50% =30 ms。

3)如果li=不存在并发活动所产生的库所，且迁移关系也没有并发关系，则计算方式为：

TL i=

∑{δ(ti,tj) ×drij,δ(tj,tk) ×drjk, ...,δ(tm’,tm) ×drm’m} =

δ(ti,tj) ×drij+δ(tj,tk) ×drjk+ ... +δ(tm’,tm) ×drm’m

(7)

4)如果li=都是并发活动所产生的库所，且迁移关系为并发关系，则计算方式为：

TL i=

max{δ(ti,tj) ×drij,δ(tj,tk) ×drjk, ...,δ(tm’,tm) ×drm’m}

(8)

2.4 算法的实现

TSRA算法和TDRA算法是以深度遍历优先算法为基础，对TPN遍历从而产生计算路径并以此计算相应时间属性。TSRA算法如下。

Algorithm1TimeSpotReasonAlgoInput：TPNOutput：estimatedtimeTSET(TPN)1)Path(TPN)=Depth＿traverse(TPN)2)Foreachpathli：;pi，pj，…pm>inSetPath(TPN)3){sett0asthebeginningtimeofli4)setpi=getPlace(li)5)While(piisnotNULL)6){setcurDur=δ(ti，tj)∗drij7)If(isPlaceParellel(pi)==true)8){setp’i=getNextPlace(li)9)setcurDur’=δ’(ti，tj)∗dr’ij10)If(curDur;curDur’)11)setcurDur=curDur’12)}setsumDur=sumDur+curDur13)setpi=getNextPlace(li)14)}15)settLi=t0+sumDur16)addtLitoTSET(TPN)17)}

3 仿真算例系统验证与分析

本文选择了某综合模块化航电系统在综合导航场景下的系统处理过程来建立TPN模型，如图3所示。TPN模型描述了在综合导航场景下以装载飞行计划、获取当前位置、计算飞行位置、修正IRS累计误差以及调整飞机姿态等库所表示的处理动作的发生流程、顺序以及每个库所之间的迁移情况，且模型中库所的描述信息如表1所示。

图3 综合航电系统综合导航场景的TPN模型

1)在综合导航场景的TPN模型中，P3和P4库所表示的是并发发生的动作，则推理时间点和时间长度约束属性时应采用(6)式和(8)式进行计算。

表1 某航电系统综合导航TPN的库所列表

2)通过综合航电系统的实际测试和统计，将库所p1～p11的时间段占比参数drij均设为60%。

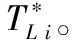
从综合导航场景TPN模型中生成了3条执行路径，并采用TSRA算法和TDRA算法分别计算出了针对每条执行路径的预计完成时间和时间长度约束，如表2所示。

表2 综合航电系统综合导航场景的时间验证

从表2所列举的预期与实际时间可以比较得出，最小的偏差为9 ms，最大的偏差为11 ms，相对于预计时间的偏差比例最小为3.5%，最大为4.3%，但均不超过5%。

为了进一步对本文所提出的方法进行验证，另外选取了航电系统地形跟随、起飞后数据检查、降落后数据检查及机电系统收起落架等5个场景进行TPN建模与时间推理计算，5个场景共验证并计算了66条执行路径的预计时间，并分析了平均偏差比例。

表3 其他应用实例中的验证情况

综合表2和表3可以看出，在多个实例系统的测试验证过程中，文中所提出的基于时间Petri网的时间推理算法，能够对系统的时间属性较准确地分析和估计，平均偏差比例不小于5%。

4 结论

本文利用Petri网具有能对系统进行动态描述和分析的特点，通过扩展Petri网的时间属性，提出了一种基于时间Petri网来分析验证航电系统时间属性和时间约束的方法。从多个系统的验证结果分析来看，该方法能够有效地对系统的时间属性进行建模和计算，具有较好地可信度，对航电系统的测试与验证有积极意义。

[1] 钟德明, 刘 斌, 阮 镰. 嵌入式软件仿真测试环境软件体系结构研究[J]. 北京航空航天大学学报. 2005,31(10):1130-1134.

[2]刘 畅, 刘 斌, 阮 镰. 航空电子软件仿真测试环境软件体系结构研究[J]. 航空学报, 2007,27(5):877-882.

[3]郑 春, 舒 坚, 牛文生, 等. 基于SysML模块定义图的集成测试序列生成方法[J]. 计算机工程与设计,2016,37(8):2067-2071.

[4]曹伟芳. 基于SysML活动图的测试序列生成方法研究[D]. 南昌航空大学, 2016.

[5]徐文华, 张育平. 基于航电系统架构模型的安全性分析工具的设计与实现[J]. 计算机科学,2016,43(11):536-541.

[6]潘 理, 丁志军, 郭观七. 混合语义时间Petri网模型[J]. 软件学报,2011,22(6):1199-1209.

[7]杨健维, 何正友, 臧天磊. 基于方向性加权模糊 Petri网的电网故障诊断方法[J]. 中国电机工程学报, 2010,30(34): 42-49.

[8]杨健维, 何正友. 基于时序模糊Petri网的电力系统故障诊断[J]. 电力系统自动化,2011,35(15):46-51.

[9]张 岩, 张 勇, 文福拴, 等. 容纳时序约束的改进模糊Petri网故障诊断模型[J]. 电力系统自动化, 2014,38(5):66-72.

TemporalAnalysisofIntegratedAvionicsSystemBasedonTimedPetriNet

Fan Xin，Zheng Wei，Liang Qijun

(School of Software, Nanchang Hangkong University, Nanchang 330063, China)

Integrated avionics system is an embedded application system with high reliability and real time requirement. In order to solve the problem such as estimating and testing processing duration during the verification of integrated avionics system more effectively, an analytical method based on Petri net with time constraints, which is named timed Petri net, is proposed in this paper. The formalized definition of timed Petri net is also introduced after analyzes the time attributes of each working node while integrated avionics system is running. By introducing the concept of temporal constraint path, the temporal reasoning algorithms are designed. At last, comparison and analysis of data collected in the simulation example system are also presented, the results show that the proposed method is feasible and effective in time verification of the integrated avionics system.

Integrated Avionics System; Timed Petri Net; Temporal Constraint Path; Temporal Analysis Algorithm

2017-08-28；

2017-10-11。

国家自然科学基金青年基金项目(61501217)。

樊 鑫(1981-)，男，湖北荆州人，讲师，主要从事软件测试技术、模型验证技术方向的研究。

郑 巍(1982-)，男，江西萍乡人，副教授，主要从事软件模型验证、社交网络分析方向的研究。

1671-4598(2017)11-0288-03

10.16526/j.cnki.11-4762/tp.2017.11.073

TP391.9

B