基于蒙特卡洛仿真的伺服舵机功耗评估方法研究

， ，，，

(中国运载火箭技术研究院研究发展中心，北京 100076)

基于蒙特卡洛仿真的伺服舵机功耗评估方法研究

郎鹏飞，刘刚，石庆峰，郑宏涛，谢泽兵

(中国运载火箭技术研究院研究发展中心，北京100076)

为了解决飞行器设计中广泛存在的重量功耗指标约束与产品实际性能需求相冲突的问题，以某重复使用运载器伺服系统功耗指标设计作为实例，首先对伺服舵机子系统电气-机构传动模型、负载力矩、工作效率等影响功耗的关键因素进行研究，建立相应的数学模型，并将之纳入飞行器制导控制系统的蒙特卡洛打靶仿真模型，在打靶仿真过程中实时计算并保存与舵机功耗相关的各项数据，作为定量评估伺服舵机整体功耗需求的依据，结果表明通过该方法确定的功耗指标相比传统方法有了较大程度的优化，该方法充分发挥了计算机数学仿真的技术优势，既可有效降低不必要的设计余量，又通过蒙特卡洛方法避免了设计过于冒进，有利于总体重量、功耗指标闭环，在重量功耗指标约束严苛的飞行器研制中具有广阔的推广应用前景。

伺服舵机；蒙特卡洛；打靶仿真；功耗评估

0 引言

伺服舵机系统是大多数航空航天飞行器的核心控制执行机构，也是除发动机外输出功率最大的子系统，通过接收控制系统输出的指令驱动被控对象(如气动舵面等)，从而实现对飞行器特定变量的精确控制，其性能很大程度上决定了控制系统的性能。伺服舵机系统按照工作原理可分为电动舵机、液压舵机和电动液压舵机3种，其中电动舵机以其突出的技术优势和经济效益，近二十年来在航空航天领域已日益占据主流。本文给出的功耗评估方法适用于电动伺服舵机系统。

对于飞行器设计而言，希望伺服系统在极限的重量功耗约束下发挥极限性能，这就要求伺服舵机必须与动力电源进行精细的耦合设计。作为一个高阶、非线性、强耦合、多变量系统，伺服舵机动态数学模型复杂，且与常规电气设备的用电特性存在很大差异，导致对其功耗的精确评估较为困难。本文以某重复使用运载器为例，对其电动伺服系统工作特点和用电方式进行研究，通过优化功耗指标，为动力电源的设计提供可信的输入，有效避免过设计，有利于总体重量功耗指标闭环，对型号研制进展的推动具有重要意义。

1 伺服系统功耗特性

伺服舵机系统由于自身的工作特点和性能要求，导致其功耗呈现出如下特性：

1)功耗波动范围大。伺服舵机系统功耗随舵面负载变化而变化，当飞行器平稳飞行时舵机负载较小，相应的功耗也较小；当飞行器进行大姿态机动时，则要求伺服舵机在较大负载力矩作用下输出高转速，往往容易出现瞬时的峰值功耗，且峰值功耗与稳态功耗相差很大，要求伺服电源具备高倍率放电能力。

2)功耗分布随机性强。飞行器伺服舵机系统峰值功耗出现的时机具有较强的不确定性，这主要体现在两方面：一是各种扰动出现时机不确定，从而使控制系统对伺服系统的控制指令分布不确定，最终导致伺服系统功耗随时间变化曲线具有较强随机性；二是飞行器通常在长时间飞行后仍可能要求对姿态进行较大调整，即在工作周期的后半程(甚至末期)仍然有峰值功耗需求，而常用的化学电源随着工作时间的延长，其输出峰值电流的能力在不断下降，这就进一步增大了伺服电源的设计难度。

3)工作效率难以确定。伺服舵机系统的工作效率定义为输出总功率与功耗之比，由定义可知伺服系统的工作效率对于功耗的精确评估至关重要。伺服舵机系统工作效率与许多内部参数相关，而且大部分参数均会随着系统运行过程而动态变化，因此为准确评估其功耗需求，不能将伺服系统工作效率简单视为常数[1-2]。

2 传统功耗评估方法

传统航天运载器、导弹等在进行伺服舵机推力及功率指标设计时，多采用基于标称设计轨迹的静态计算方法，具体如下：

1)针对飞行器标称轨迹，在不考虑偏差因素的情况下，通过制导控制系统输出的与舵面偏转相关控制指令计算出标称轨迹下伺服舵机的输出功率曲线P(t)；

2)选取上述曲线中的功率最大值Pmax，并考虑偏差干扰因素(通常乘以某常数项k，k>1，根据型号实际情况进行取值)，将kPmax作为伺服舵机系统的全程峰值功耗；

3)根据公式“功耗=输出功率/工作效率”计算伺服舵机常值功耗，其中输出功率按照工程经验取kPmax的1/n(n>1)，工作效率则按照经验取选取某介于0～1的常数；

4)将上述步骤计算出的伺服舵机常值功耗作为常值放电功率进行电源系统容量设计，电源极限放电能力设计则通常基于工程经验及飞行器具体任务剖面人工拟合峰值功耗特性。

采用传统评估方法所确定的伺服舵机系统功耗指标难以准确反应舵机工作中各种非线性因素及不确定因素，往往存在过于保守的现象，导致伺服舵机电源的包络尺寸、重量均较大，对总体指标闭环造成不利影响[2]。

3 基于仿真的功耗评估方法

3.1 问题及对策分析

为解决传统功耗评估方法存在过于保守的问题，研究团队对影响伺服舵机系统的各项要素及其构成进行研究分析，结果如图1所示。

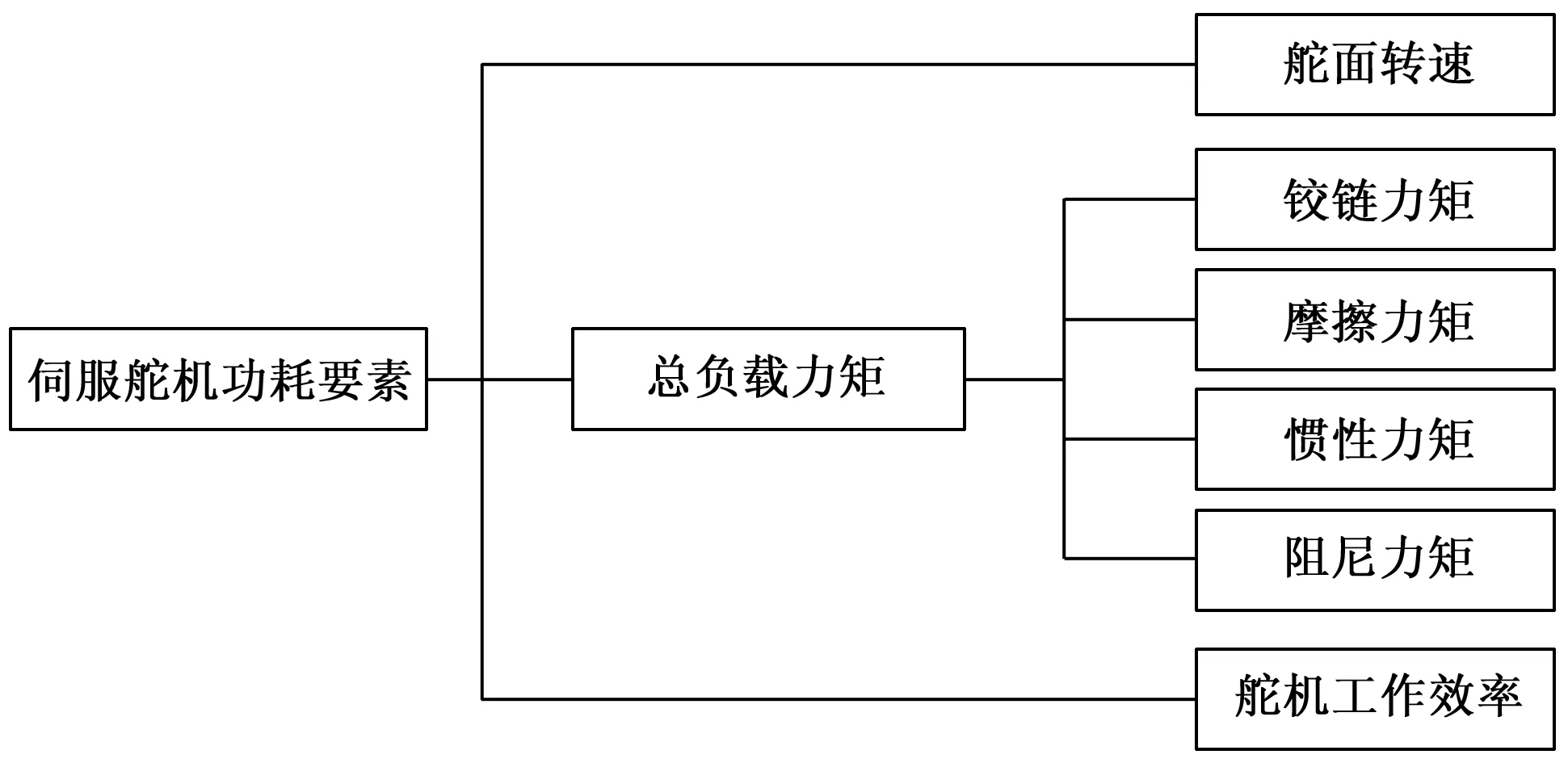
图1 伺服舵机功耗要素分析

对于图1中所列举的影响伺服舵机功耗的6项因素，可分为以下4类：

1)摩擦力矩、阻尼力矩仅与舵机-舵面传动机构参数相关，可直接静态计算；

2)铰链力矩、惯性力矩既与机构静态参数相关，又与舵机实时工作状态相关；

3)舵面转速与制导控制指令及舵机传递函数相关；

4)舵机工作效率最为复杂，需通过理论建模、单机试验验证及工程经验拟合计算公式。

通过上述分析，可见仅通过静态计算难以获取与伺服舵机功耗相关的所有因素，部分重要因素由于与伺服舵机系统的实时工作状态相关，无法通过静态计算的方法获得。为准确获取相关数据，可将上述各项要素的计算方法纳入控制系统的打靶仿真模型，通过仿真实时获取功耗评估所需数据[3]。

3.2 建立功耗计算模型

对于常规的舵面驱动伺服系统，具有如下基本运算关系：

(1)

式中，P为伺服系统功耗，W为伺服系统输出功率，η为伺服系统工作效率，M为舵面总负载力矩，ω为舵面转动角速度，因此对伺服系统功耗的评估就在于如何精确的确定其负载力矩M、舵面转动角速度ω及工作效率η。

1)负载力矩分析。

通过对负载力矩M的进行全面分析，可得到其构成如下：

M=Mh+Mi+Mf+Md

(2)

式中，Mh为舵面铰链力矩，Mi为惯性力矩，Mf为摩擦力矩，Md为阻尼力矩，对于各项力矩均有相应计算公式：

Mh=Cmh×Q×Sref×Lref

(3)

(4)

Mf=M0+M1+M2

(5)

Md≈0相对其他力矩可忽略不计)

(6)

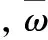
2)舵面转速分析。

舵面转动角速度ω是飞行器制导控制系统的输出，可在控制系统的仿真中通过对制导控制模块输出的指令舵偏角(需考虑舵机传递函数)进行微分运算实时获取。

3)工作效率分析。

对于舵机工作效率η，通过对电动伺服舵机工作原理的研究分析，结合理论建模、单机试验验证及工程经验等多方面的工作，确定了如下计算公式：

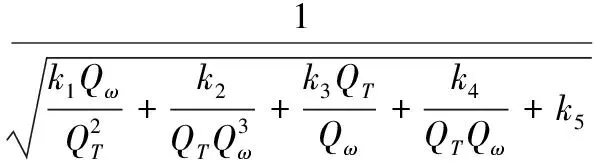
(7)

式(7)中，QT为实际-额定力矩比，Qω为实际-额定转速比，k1～k5均为经试验确定的常数[6]。

3.3 蒙特卡洛打靶仿真

蒙特卡洛方法又称随机抽样或统计试验方法，是一种基于“随机数”的计算方法，通过设定随机过程，反复生成时间序列，以概率模型为基础，计算特定参数的估计量和统计量，进而研究其分布特征，能够真实的模拟系统的实际物理过程，因此能够更贴近系统实际状况，得到符合预期的结果。

基于3.2章节中公式(1)～(7)所确定的伺服舵机系统功耗计算方法，在飞行器制导控制仿真模块中加入相应数学运算模型，并通过实施蒙特卡洛打靶仿真实现对伺服舵机系统的功耗评估。

对于本文所研究的某重复使用运载器打靶仿真工作，基于常规的MATLAB/Simulink仿真平台，采用刚体六自由度运动模型，根据飞行器总体原始数据、全飞行器气动特性数据、舵面气动特性数据，设定仿真模型初始条件参数，考虑的偏差因素包括初始条件(位置、速度)偏差、质量特性(质量、质心位置、转动惯量)偏差、气动系数偏差、动力参数偏差、大气密度偏差、风干扰等，按照蒙特卡洛方法开展10 000次打靶仿真，具体仿真流程如图2所示[7]。

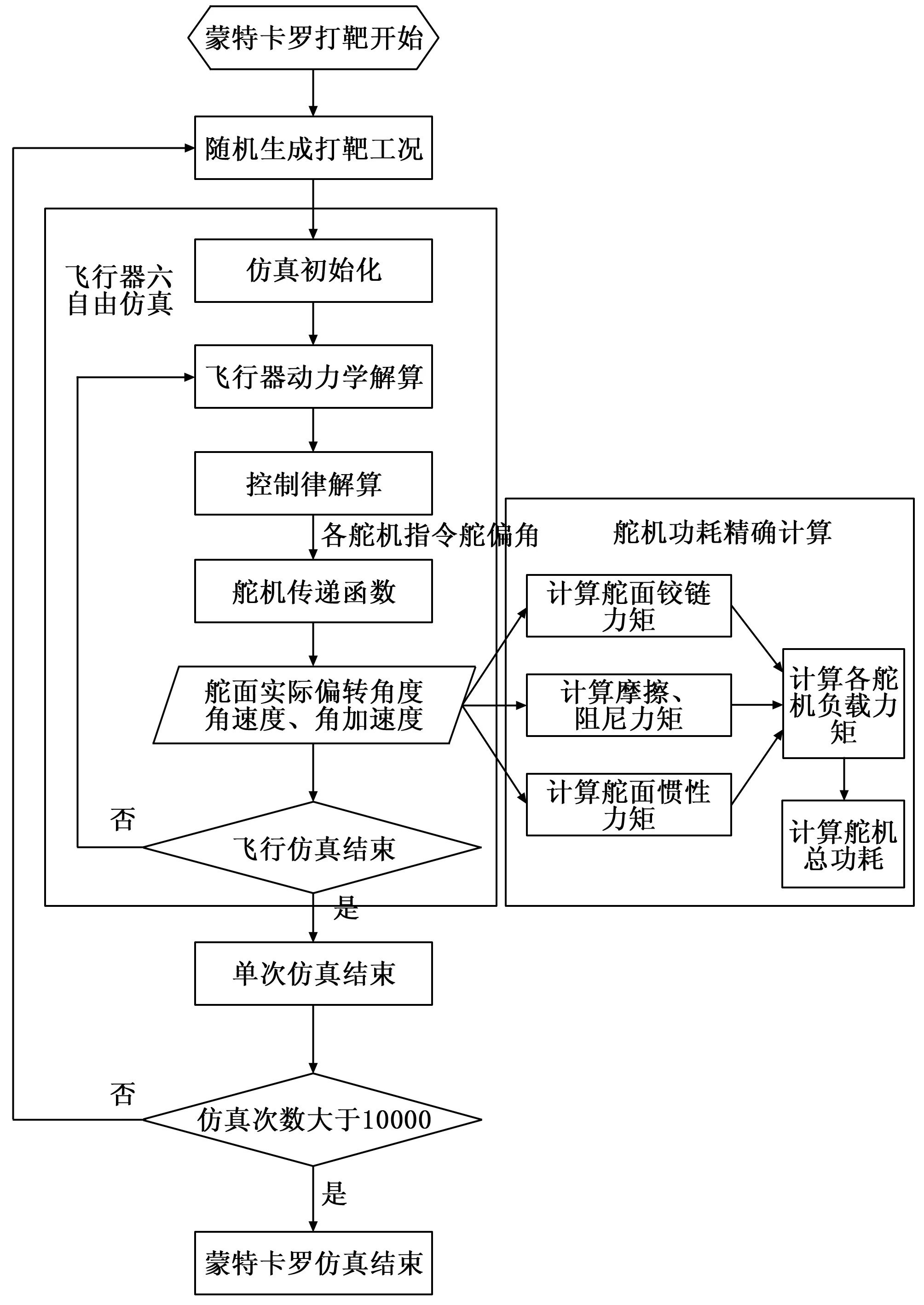
图2 蒙特卡洛打靶流程

3.4 数据处理与功耗评估

3.4.1 处理思路

按照上文所述的打靶仿真流程，基于某重复使用运载器的制导控制模块，按照蒙特卡洛方法考虑各种随机偏差组合实施10 000次重复打靶仿真，可得到伺服舵机子系统在不同工况下功耗随时间变化曲线。如何采用高效、科学的方法从海量数据中提取关键特性，是实现对伺服舵机系统功耗精确评估的重点和难点。

由于目前电动伺服舵机系统多采用高压高功率蓄电池组作为能源，其设计指标主要受电池容量(主要与伺服系统长时间稳态工况相关)、放电能力(主要与伺服系统极限工况相关)两方面的约束，因此对功耗数据的处理也主要从全程平均功耗及峰值功耗两方面进行。

1)稳态功耗处理方法。

伺服舵机系统稳态功耗(可等效为平均功耗)主要表征其在大多数时间内的工作状态，在打靶仿真过程中可按照如下公式进行实时计算：

(8)

(9)

2)极限功耗处理方法。

极限功耗通常出现在飞行器需进行较大程度的姿态机动时，按照第1章节分析，其具有分布随机、持续时间短、与稳态功耗值相差较大等特性，对蓄电池组的极限放电能力有较大影响，用于表征极限功耗特性的主要因素包括峰值功耗的幅值、持续时长、频次等。为评估峰值功耗情况，需首先基于伺服系统电源串并联体制选取功耗基准：当伺服舵机总功耗大于该基准时，认为进入峰值功耗区间，即电源进入高倍率放电状态；当功耗低于该基准时，认为伺服系统处于常值功耗区间。通过对本飞行器的高压蓄电池组体制供电能力进行分析，该基准设为4 kW，之后从仿真数据中统计与舵机峰值功耗相关的各项参数用于定量评估舵机极限工况下的功耗需求。

3.4.2 仿真数据统计

为便于统计分析，选取本飞行器某台伺服舵机为例，按照3 σ原则，统计10 000次打靶中，该舵机的最大瞬时功率、电源功耗、平均功耗、峰值功耗区间(即功耗超过4 kW基准的区间)个数、每个峰值区间的最大功率、峰值区间持续时长、相邻两峰值区间间隔等数据，具体数据统计如表1所示。

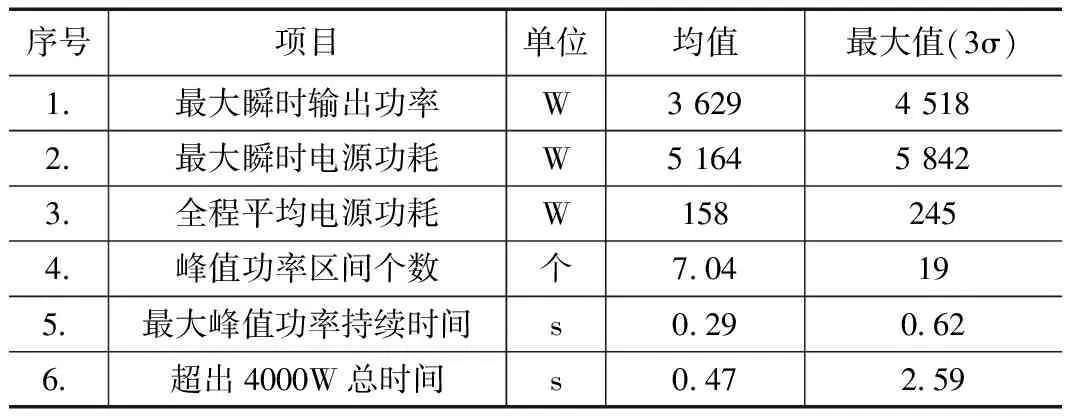
表1 舵机功耗相关数据统计

3.4.3 优化效果分析

为更直观的判断采用本研究所使用功耗评估方法的优化效果，需将通过蒙特卡洛打靶仿真所得到的功耗情况与传统经验估算法进行对比。

对于伺服舵机稳态(平均)功耗，按照第2章节中所描述的传统功耗估算法计算出舵机平均功耗为1 389 W；对于舵机极限工况下的功耗，结合本飞行器伺服系统性能及飞行任务剖面，按照传统工程经验估算，其功耗峰值取8 kW，峰值功耗总持续时间为该舵机总工作时间的2%，其中每次峰值功耗持续时间为1 s，整个飞行过程中出现峰值功耗的次数不大于50次[8]。

根据表1中的统计结果，将通过蒙特卡罗打靶仿真所获取的舵机功耗指标(为规避由于仿真采样周期所造成的设计风险，另行考虑20%设计余量)与传统估算法所得到的功耗指标进行对比分析，结果如表2所示。

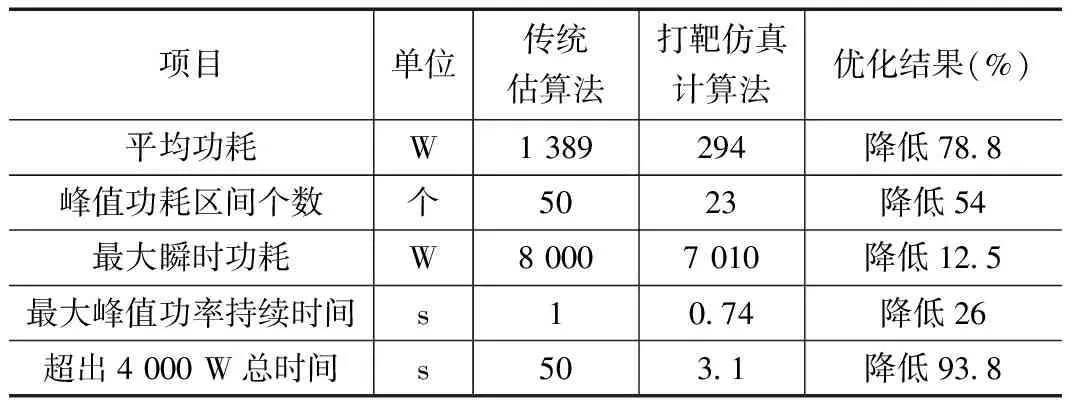
表2 舵机功耗指标优化情况

通过表2中的对比分析可明显看到，按照本文所提出的基于蒙特卡洛打靶仿真的功耗评估方法所确定的伺服舵机子系统稳态及极限工况下的功耗需求相比传统工程经验估算法确定的功耗需求均有较大程度的优化，将该功耗指标作为伺服舵机电源设计的输入，可有效降低蓄电池组的重量、体积，为飞行器总体指标的闭环做出贡献。

5 结束语

本文结合某重复使用运载器伺服功耗指标设计实例，给出了一种基于蒙特卡罗打靶仿真的伺服舵机功耗评估方法，该方法将伺服舵机功耗评估纳入制导控制系统方案设计与仿真中，与航天领域目前广泛使用的基于工程经验的伺服系统功耗评估方法相比，大大改进了设计效率，可有效避免由于指标设计过于保守而带来的伺服舵机及其配套电源重量、功耗大幅增加，又通过蒙特卡洛打靶仿真验证避免了设计过于冒进而导致的灾难性后果，在我国未来各种新型航空航天型号(尤其是对重量、功耗约束较为苛刻的型号)研制过程中具有重要的推广应用价值。

[1]李 志, 李明华译. 航空舵机系统设计引论[M]. 北京: 航空工业出版社, 2013.

[2]党 坤. AEG型舵机液压伺服系统的功率流建模[A]. 中国机械工程学会第三届全国青年学术会议论文集[C]. 北京: 中国机械工程学会, 1998: 135-138.

[3]黄玉平, 李建明 朱成林. 航天机电伺服系统[M]. 北京: 中国电力出版社, 2013.

[4]余 波. 飞行器舵机传动机构设计与性能分析[D]. 重庆: 重庆大学, 2014.

[5]张习强. 飞行器舵机伺服传动机构动力学建模研究[D]. 南京: 南京航空航天大学, 2013.

[6]张学军. 直九旋翼功率传递系数确定方法研究[A]. 第二十一届全国直升机年会论文集[C]. 天津: 中国航空学会, 2005: 610-615.

[7]John M. Hanson, Bernard B. Beard. Applying Monte Carlo Simulation to Launch Vehicle Design and Requirements Verification. Journal of Spacecraft and Rockets [J] .2012,49(1):53-61.

[8]张 艳, 王 勇,等. 一种基于负载匹配的伺服功率优化方法. 导弹与航天运载技术[J], 2016, (4):72-74.

ResearchonPowerEstimationMethodofServoActuatorBasedonMonteCarloSimulation

Lang Pengfei， Liu Gang， Shi Qingfeng， Zheng Hongtao， Xie Zebing

(China Academy of Launch Vehicle Technology R&D Center，Beijing 100076，China)

To solve the problem that product’s actual performance requirements usually conflict with index constraint, Take a reusable launch vehicle’s servo system power quota design as an example, firstly, the key factors affecting power consumption are studied, and the mathematical model is established and incorporated into control system’s Monte Carlo simulation. Through simulation, the relevant data is obtained and used to evaluate the power consumption, which not only reduces unnecessary design margin, but can also avoid aggressive design, and has a wide application prospect.

servo system; Monte Carlo; simulation; power dissipation evaluation

2017-06-18；

2017-07-17。

郎鹏飞(1988-)，男，河南新郑人，硕士研究生，工程师，主要从事控制系统电气综合方向的研究。

1671-4598(2017)11-0276-04

10.16526/j.cnki.11-4762/tp.2017.11.070

TP3

A