链式多智能体遗传算法在分布式电源全时序上优化配置
,,,
(南昌航空大学 信息工程学院,南昌 330063)
链式多智能体遗传算法在分布式电源全时序上优化配置
杨宏超,程若发,贺志华,吕彩艳
(南昌航空大学信息工程学院,南昌330063)
分布式电源的选址与定容是微电网研究所面临的重要问题,提出一种考虑规划地区的24-h负荷时序特性和气候特点的24-h负荷变换情况下的DG优化配置;为了解决上述问题,采用链式多智能体遗传算法对其进行优化处理;首先通过算法对IEEE33节点系统进行测试,验证算法在分布式电源优化配置中的优越性,并对PG&E69节点配电网进行24-h时序的全过程模拟仿真优化,结果验证了多智能体遗传算法能在分布式电源配置上的有效性,同时提高微电网接入的预测精度,加快收敛速度,改进陷入局部最优的可能性等问题,对微电网在规划选址与定容选择上提供工程参考的实用性。
微电网;分布式电源;有功网损;选址和定容;多智能体算法
0 引言
随着大量DG接入配电网,使配电网从无源网络变成有源网络,大量DG在电网中随机并网与孤岛运行将使电力系统负荷预测更不稳定,同时使预测负荷的增长情况变得更加困难。所以考虑时序全过程模拟将使规划更有实际意义,也更利于真实的反映配电网各项经济技术指标,以及实现风、光资源的互补。根据配电网中分布式电源种类的不同来研究经济的优化运行策略,有的仅考虑风、光互补系统,有的同时考虑风光储联合运行,并重点研究储能装置的运行特性。机组的组合需要分别考虑可再生能源发电、不可再生能源发电和可中断负荷等,此外还需考虑冷热负荷,通过对能源梯级利用进行优化[1]。文献[2-3]考虑在电力市场的峰谷电价和负荷转移等情况下,对配电网的电能质量、供电可靠性、安全性、经济性的研究。文献[4]提出采用改进的PSO算法对DG选址与定容进行研究,其主要目的是使配电网的损耗进一步减少。文献[5]提出在配电网扩展规划中进行DG选址定容,但该算法易陷入局部最优解。文献[6]以利益成本为目标函数,采用GA算法对DG位置和容量进行优化。文献[7]采用多种典型的场景进行模拟负荷与DG的时序性,此方法虽有利于减少工作量,但易造成较大误差。对于风力发电方式与光伏发电方式等不可控的发电,其出力大小主要由当地的地理环境决定。因此,考虑如何将DG全程时序化模拟,这更利于反映真实的配电网的各项经济指标,同时有利于实现风光互补。文献[8]主要考虑负荷水平对DG进行选址定容规划,但只考虑部分特定负荷水平,并未全程考虑负荷时序特性及DG出力情况。文献[9]虽涉及基于日负荷曲线,规划时仅通过单目标寻优考虑在孤立场景下的情况,使规划结果具有局限性。为了解决上述问题和缺陷,本文提出链式多智能体遗传算法利用网络有功网损和静态电压稳定性双指标对分布式电源进行优化配置,并通过24 h全时序模拟验证其准确性。
1 目标函数建立与优化
配电网规划是为了满足用户供电,确保网络在寻求一组最优决策变量的约束下正常运行,系统中有功网损最小,电压稳定等指标保持在一定限度内 ,所以引入以下指标和约束条件。
1.1 目标函数
1.1.1 配电网系统有功网损指标
系统的目标函数表达式[10]如下:
(1)
式中,fploss为系统的有功损耗;N为系统的节点数;rb为对应支路的电阻;Pi和Qi为网络向节点i注入的有功和无功功率;Ui为支路b首节点i的电压幅值;
1.1.2 电压稳定性指标
根据潮流解作为判据,得出改进的电压稳定性指标如下:
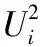
(2)
式中,Ustab,k为对应支路上的电压稳定指标;R和X为支路k的电阻和电抗;Pi和Qi为末节点流入的有功功率和无功功率;Ui为各支路首节点的电压幅值。
所有分支的最大电压稳定指标为系统电压稳定指标如下式所示:
fUstab=max{Ustab,1,Ustab,2,...,Ustab,N}
(3)
式中,N为网络节点总数,Ustab,1,Ustab,2,…,Ustab,N分别为1,2,…,N支路的电压稳定性指数。
1.1.3 综合目标函数
为了进一步综合各单一目标,采用权重系数法将它们结合在一起转化成单目标进行优化。数学模型如下:
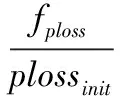
(4)
式中,f为双目标优化函数;plossinit与Ustabinit是初始状态下的有功损耗与静态电压稳定指数;a、b分别为有功损耗与静态电压稳定性指数的惩罚因子;ω1和ω2分别是网络有功损耗和静态电压稳定指数的权重因子,ω1+ω2=1。
式中,a定义为:
(5)
当优化后的有功损耗大于初始有功损耗,则将a值设定成一个大正数N,即增大f的值,放弃此解;相反,a=1。
b定义为:
(6)
如果优化后静态电压稳定性比初始静态电压稳定性差,则将b值设定为一个大正数N,即增大f的值,放弃此解;反之,b=1。
1.2 约束条件
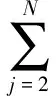
(7)
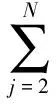
(8)
Uimin≤Ui≤Uimax
(9)
Sij≤Sijmax
(10)
PDGimin≤PDGi≤PDGimax
(11)
式中,PDGi和QDGi为系统向节点i注入的有功功率和无功功率;2≤i≤n;PLi和QLi为第i个节点上的有功负荷功率和无功负荷功率;Gij,Bij和θij为节点i到节点j之间的电导、电纳和相角差;Ui和Uj为对应节点上电压幅值;Sijmax为支路i、j的最大容许容量;PDGi为节点容量范围。
2 链式多智能体遗传算法介绍
针对基本遗传算法易早熟易收敛的现象,提出了一种改进基因操作后的遗传算法即链式竞争策略的智能体遗传算法(Link-like Agent Genetic Algorithm,LAGA)[11]。LAGA 引入了链式网络智能体结构,所有智能体都放在一个规模为1×SLsize的循环链式网格上,每个智能体都有局部感知能力,可与相邻智能体相互作用,通过比较邻域智能体之间的适应值大小,从而达到优胜劣汰的效果。
假设处于(1,i)格点的智能体表示为L1,i(i=1,2,…,SLsize),L1,i的邻域LneiborSi定义如下:LneiborSi{L1,i,L1,i},其中:
(12)
如图1其中圆圈代表智能体,数字代表位置。

图1 链式多智能体网络结构
在链式网络结构中智能体个体之间会进行动态邻域竞争、正交交叉和自适应变异操作来更新自己的个体信息。接下来,介绍LAGA的个体更新规则。
1)动态邻域竞争算子。
假设当前智能体位于(1,i)格点L1,i=(li,1,li,2,…,li,n),Max1,i=(mi,1,mi,2,…,mi,n)为L1,i的邻域中能量最大的智能体,其中n为变量个数。即:,∀a∈LneiborS1,i,enger(a)≤enger(Max1,i)都成立。如果L1,i满足方程energy(L1,i)>energy(Max1,i) ,则可继续存活在智能体结构中,则必须死亡,空出的格点将被New1,i=(nei,1,nei,2,…,nei,n)占据。
2)正交交叉算子。
在链式智能体遗传算法中,正交交叉算子是将L1,i和Max1,i两父代个体寻求两子代个体的过程,转换为F因素Q2水平的正交试验,从正交表A4(23)中获得能量最高的两种组合作为两个子代。
3)自适应变异算子。
在相对定义域的个体加上位的高斯扰动,实现小范围内的变异。按照下式产生新的智能体New1,i=(ne1,ne2,…,nen)。
(13)
式中,Pm表示变异概率设为1/n;G(0,1/t)产生高斯分布的随机数,t为当前进化数。
LAGA算法按以下步骤执行:
步骤一:初始化参数;
步骤二:构造链式网络系统的规模1×SLsize,初始化种群,迭代次数T, 交叉概率Pc,变异概率Pm等;
步骤三:计算各个智能体能量;
步骤四:种群个体更新;依次对每个智能体通过根据(1)、(2)和(3)步骤进行动态邻域竞争、正交交叉和自适应变异并更新种群信息;
步骤五:适应度函数值计算;
步骤六:判断是否符合终止条件,若符合则结束迭代同时输出结果。否则,T=T+1,,跳转到步骤二。
3 算例分析
3.1 验证算法适用性算例
首先为了验证算法在分布式电源优化配置的有效性,本文选取在IEEE33节点网络以非恒定功率因素的PQ节点类型DG进行优化,其中PQ节点类型DG功率因素在0.90~1.0范围内变动。由于QPSO算法[12]在DG优化配置上算比较成熟的算法了,所以将本文算法LAGA和QPSO算法进行比较,使结果更具一般性。两种算法的配置结果如表1所示。

表1 两种算法DG优化配置结果
通过表1可以明显看出QPSO和LAGA算法都能正确的优化非恒定功率因素PQ节点类型DG的优化配置。相较于QPSO算法,LAGA在有功损耗上有所降低。说明LAGA在节点优化配置上具有一定的优越性。
图2和图3给出了QPSO和LAGA两种算法的寻优曲线和系统节点电压幅值曲线。从图2中可以看出,LAGA具有更快的收敛速度,且收敛曲线相较于QPSO要更好一些;说明LAGA算法相较与QPSO在收敛速度和收敛精度上都有一定的优越性。从图3系统节点电压幅值的整体走势上分析看LAGA算法的节点电压总趋势值都要低于QPSO算法,证明算法具有一定的优越性。综上,通过对IEEE33节点网络的仿真分析,并通过与QPSO算法的比较,证明本文LAGA算法在DG优化配置上具有一定的优越性和可适用性。
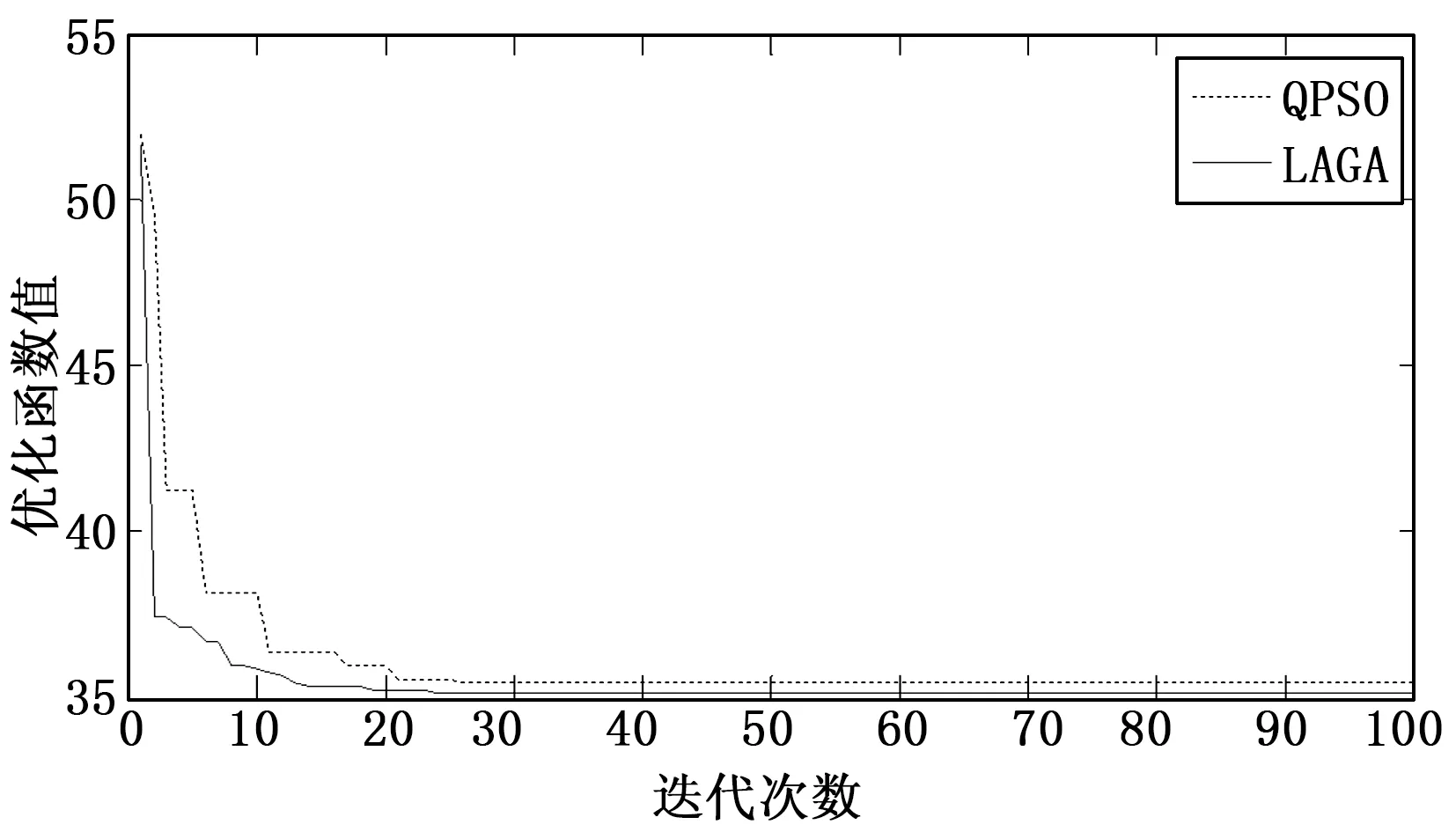
图2 两种算法的收敛特性曲线
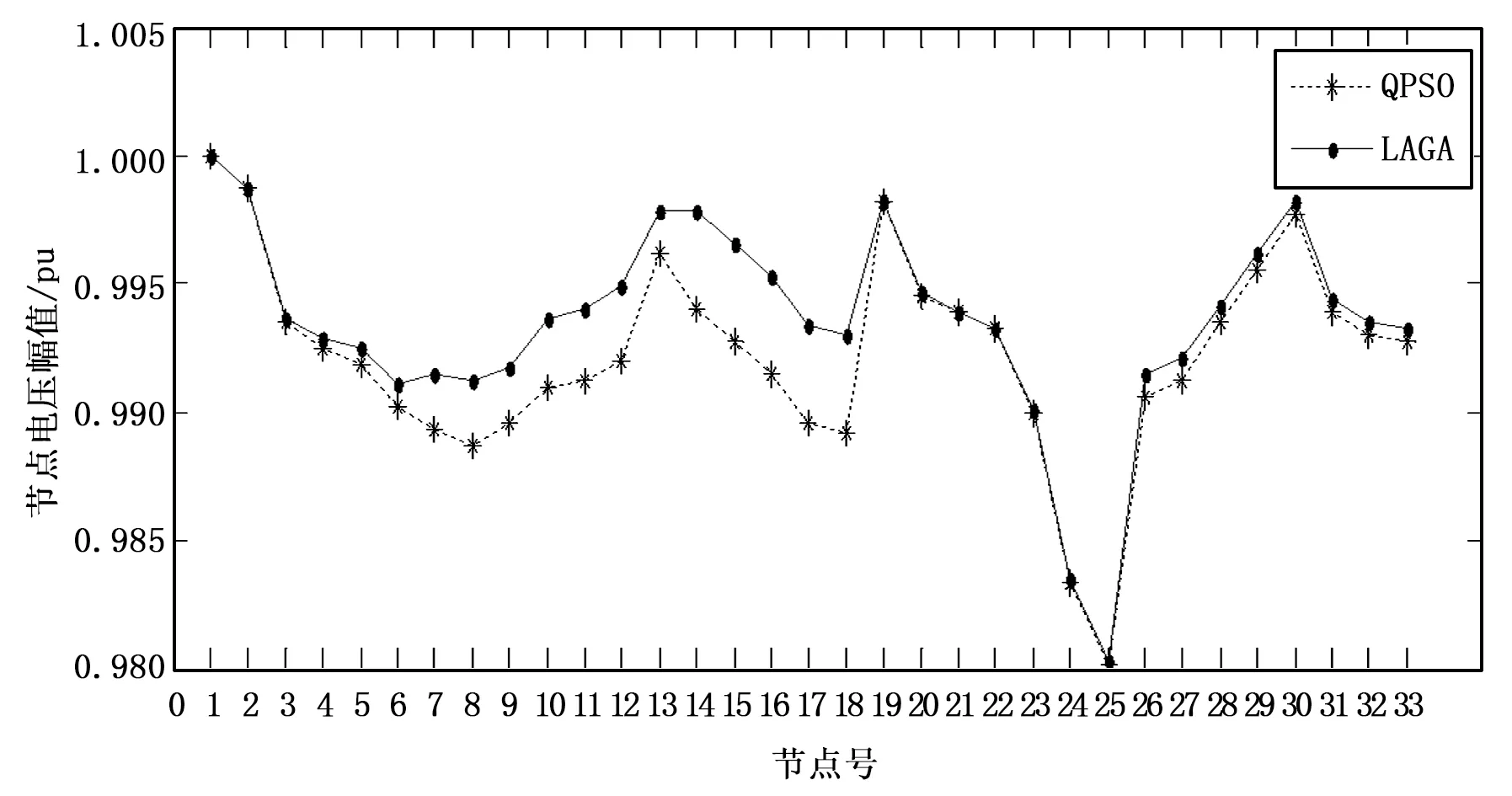
图3 两种算法的系统节点电压幅值
3.2 全天24 h时序过程模拟仿真算例分析
上述已经证明提出的算法在DG优化配置中的优越性,下面说明LAGA在DG优化配置中的应用,主要考虑时序的全过程模拟对DG选址和定容。首先对规划地区的负荷时序特性和气候特点的统计资料进行分析,得出具有代表性的场景及其权重,然后基于负荷和DG的时序特性进行分布式电源的选址和定容。负载24-h序特性曲线如图4;风力发电和光伏发电24-h输出时序特性曲线如图5[13]。
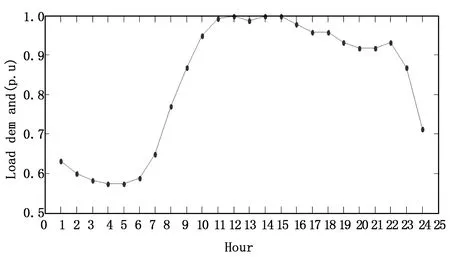
图4 负载24-h时序特性曲线
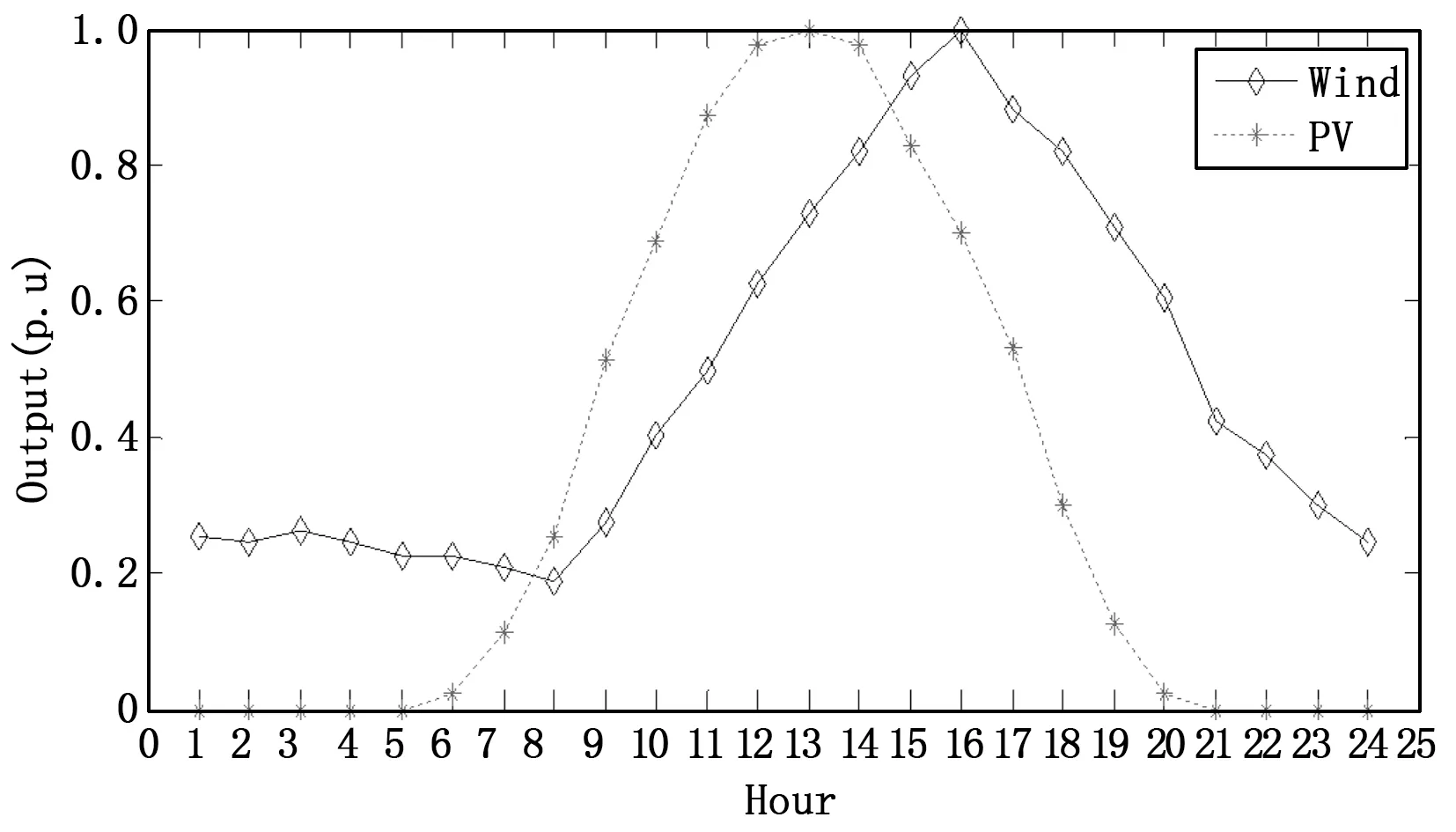
图5 风电和光电的24-h输出时序特性曲线
为了进一步体现本文算法在处理全时序条件下的分布式电源的优化配置上的可行性,采用PG&E69节点配电系统进行仿真测试,PG&E69节点配电系统如图6所示,该系统中有68条支路、5条联络开关支路、1个电源网络,首端基准电压12.66 kV、三相功率准值取10 MVA、网络总负荷3 802.19+j2694.60 kVA。分布式电源的接入依然采用潮流计算的方法,收敛精度设为10-6,种群数量为50,最大迭代次数为100,交叉率和变异率分别设为0.98和0.03。本次采用双目标函数测试,即本次测试过程选取式(4)所表示的系统有功损耗作为目标函数。

图6 PG&E69节点配电系统

图7 负载24-h在MVA的曲线
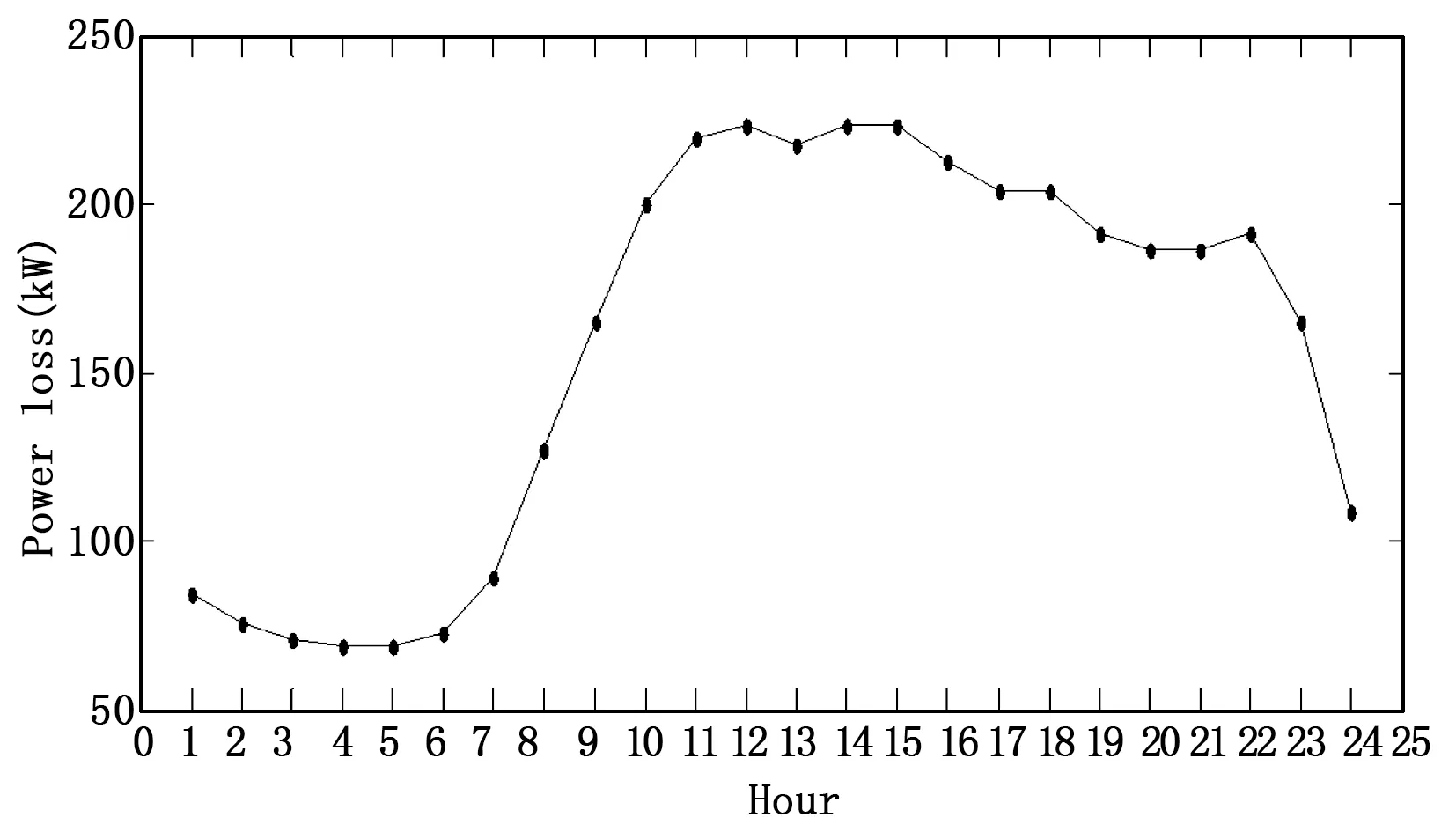
图8 配电网24-h有功损耗曲线
在没有DG接入配电网系统时,假设系统负载每天的标幺值变化曲线如图7所示,那么当系在正常运行时,系统每天的实际负载容量变化(MVA)曲线如图8所示,通过仿真测试得系统在一天内的有功损耗变化曲线如图8 所示。对仿真曲线进行分析:在凌晨一直到六点钟,由于大部分人都在休息,用电量减少,因此接入的负载较少,系统的有功损耗也相应的比较低,在七点到晚上十点,用电量需求增加,所接入的负载也就相应的增多,由于没有其他电源的补充,导致有功损耗一直维持在很高的阶段。在十一点到十二点,由于人们的用电量又有所下降,那么系统的有功损耗也相应的降低了。
案例一:在区域Ⅲ风力发电系统入网运行研究,并通过改变位置、功率因素和系统容量来进行讨论,得出优化条件选取对DG网络优化的影响。
情况A:指定风力发电系统容量,优化DG接入位置和功率因素
情况B:指定风力发电系统容量、位置和功率因素
B1:指定与A一致的容量、功率因素对位置进行优化
B2:指定与A一致的容量、位置对功率因素进行优化
情况C:指定风力发电系统位置和功率因素,优化功率接入容量
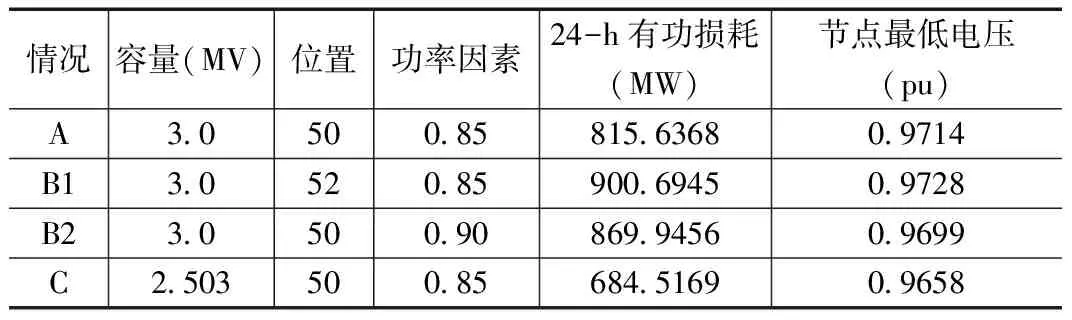
表2 优化配置结果

图9 案例一负载24-h在MVA的曲线
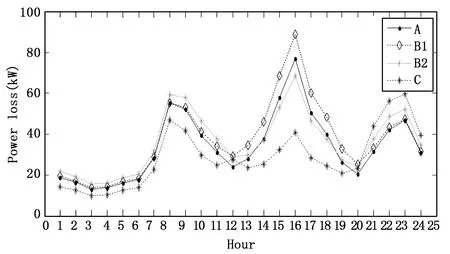
图10 案例一配电网24-h有功损耗曲线
在方案一中,本文分析了风力发电在不同种接入方式情况下对系统的影响,A是在指定容量的情况下,优化功率因素和接入位置。B为了与情况A做进一步的比较,因此分了两种情况,B1为了和A仅通过接入位置的不同作比较,B2是仅通过功率因素不同与A比较。C是为了验证与A在容量上的差异对系统有功损耗的影响。因此A和B的负载容量相同,而C与A、B不同,如图9为各方案下的负载容量曲线。比较表2数据可知,由A与B的比较可知,由于B中只是优化了其中一个变量,因而在有功损耗上都要高于A,虽然B2在节点电压上比A更好,但是从综合上考虑,A还是优于B。这同时也表明了通过优化位置和功率因素的方法是相对可取的。C通过在A的基础上优化接入容量,使得系统的有功损耗从815.6368 MW降为684.5169 MW,降低了16.08%。由图10所示,C曲线在有功损耗上要明显优于A、B1和B2,虽然在20:00-24:00时间段的有功损耗要高于A、B1和B2,但相比于12:00-20:00的降损来说还是可以接受的。因此,通过分类优化比较得出:通过位置、容量及功率因素同时寻优来进行DG的优化配置是非常合理且正确的。
案例二:针对配电网中接入DG的种类和位置不同,对不同数量DG接入配电网限制区域中的运行研究。
情况A:在Ⅲ区域内接入一个分布式电源。
A1:接入一个光伏发电系统;
A2:接入一个风力发电系统。
情况B:在Ⅰ区域接入一个光伏发电系统, 在Ⅲ区域接入一个风力发电系统。
情况C:在Ⅰ区域接入一个光伏发电系统, 在Ⅲ区域接入两个风力发电系统。
在案例二中,通过分3种情况进行讨论,分别是接入一个DG、两个DG和3个DG。结合表4-3和图4-10可得:(1)通过比较情况A可知:对于同为接入一个DG的系统,接入风力发电系统比接入光伏发电系统的降损要更好,接入光伏发电系统一天的有功损耗是1 885.92kW,而接入风力发电系统一天的有功损耗是684.517kW,同比下降了63.7%;(2)通过比较情况B可知:当同时接入光伏发电和风力发电时,系统的有功损耗为659.006kW,由于风光互补的原因,使得有功网损相对情况A1下降了65.06%,相对于A2下降了3.73%。节点电压的稳定性能也有所提高,节点的最低电压也从0.9372 pu提高到0.965 9 pu。(3)通过比较情况C可知:当同时接入3个DG时,系统的有功损耗再一次从659.006 kW降为632.775 1 kW,有功损耗减少了3.98%,系统电压的稳点性也相对的提高了,节点最低电压从0.965 9 pu升高到0.966 9 pu。因此,不同的接入方式,不同的接入条件,对于配电网系统都会产生不同的影响,但是能对接入的DG合理的优化配置,就能使系统的运行更稳定。对于不同DG数量接入配电网系统中,提出的算法对电网全时序下进行了很好的优化和处理,对不同的运行状态下都能很好的寻找到最优的配置方案。

表3 案例二优化配置结果
4 结论
综上所述,通过两个算例进行仿真测试,先在IEEE33节点上进行了静态的含分布式电源并网仿真测试,针对以非恒定功率因素的PQ节点类型DG进行优化,并通过不同算法进行比较从而验证LAGA算法在配电网中的可适用性,接着继续在IEEE69节点进行了24-h动态的含分布式电源并网仿真测试,针对不同种方案,不同种情况进行讨论,证明了无论是静态的还是动态的含分布式电源并网,本文提出的算法都能很好的解决这一系列问题,并且还能给出有效的解决方案。在配电网中合理的接入DG能够在不同程度上减少系统的损耗,提高系统的电能质量。通过最后两个算例的比较分析,体现出了合理的优化配置分布式电源接入配电网的重要性,为解决微电网的定容和选择等实际问题提供了较好方法。
[1] 麻秀范. 含分布式电源的配电网规划与优化运行研究[D].北京:华北电力大学(北京), 2013.
[2]梁才浩, 段献忠. 分布式发电及其对电力系统的影响[J]. 电力系统自动化, 2001, 25(12):53-56.
[3]梁有伟, 胡志坚, 陈允平. 分布式发电及其在电力系统中的应用研究综述[J]. 电网技术, 2003, 27(12):71-75.
[4]刘 波, 张 焰, 杨 娜. 改进的粒子群优化算法在分布式电源选址和定容中的应用[J]. 电工技术学报, 2008, 23(2):103-108.
[5]王成山, 陈 恺, 谢莹华,等. 配电网扩展规划中分布式电源的选址和定容[J]. 电力系统自动化, 2006, 30(3):38-43.
[6]海晓涛, 徐 岩, 姚晓玲. 基于免疫遗传算法的智能配电网分布式电源选址定容[J]. 陕西电力, 2011, 39(12):58-61.
[7]李 亮, 唐 巍, 白牧可,等. 考虑时序特性的多目标分布式电源选址定容规划[J]. 电力系统自动化, 2013, 37(3):58-63.
[8]薛恒嵩. 基于OpenDSS的配电网三相潮流计算[D]. 南京:东南大学, 2014.
[9]Ziari I, Ledwich G, Ghosh A, et al. Optimal allocation and sizing of DGs in distribution networks[A]. Power and Energy Society General Meeting[C]. IEEE Xplore, 2010:1-8.
[10] 鞠 平, 陈 谦, 熊传平,等. 基于日负荷曲线的负荷分类和综合建模[J]. 电力系统自动化, 2006, 30(16):6-9.
[11]曾孝平, LI Yong-Ming, 王 靖,等. 基于竞争策略的链式智能体遗传算法用于特征选择的研究[J]. 系统仿真学报, 2008, 20(8):1973-1979.
[12]关万琳. 分布式电源优化配置与配电网重构[D]. 长沙:湖南大学, 2014.
[13]Hung D Q, Mithulananthan N, Bansal R C. Analytical strategies for renewable distributed generation integration considering energy loss minimization[J]. Applied Energy, 2013, 105(2):75-85.
Multi-AgentGeneticAlgorithmforOptimalConfigurationofDistributedPowerSupply
Yang Hongchao, Cheng Ruofa, He Zhihua, Lv Caiyan
(School of Information Engineering, Nanchang Hangkong University, Nanchang 330063)
The location and capacity of the distributed power supply are the important problems in the microgrid research, and propose a DG optimal configuration considering the 24-h load timing characteristics and climatic characteristics of the 24-h load in the planning area. In order to solve the above problems, the chain multi-agent genetic algorithm is used to optimize it. Firstly, the algorithm is used to test the IEEE33 node system to verify the superiority of the algorithm in the optimal configuration of the distributed power supply. The whole process simulation of the 24-h timing of the PG & E69 node distribution network is optimized. The results show that the multi-agent genetic algorithm can improve the efficiency of micro-grid access, improve the convergence speed, improve the possibility of falling into the local optimal and other issues, the micro-grid in the planning site and the choice of capacity to provide the project reference to the practicality.
microgrid; distribution network; active network loss; position and capacity; multi-agent
2017-05-03;
2017-05-26。
国家基金项目(51567019);江西省教育厅项目(GJJ150757);江西省科技支撑计划项目(20142BBE50002)。
杨宏超(1991-), 男,安徽滁州人 ,硕士研究生 ,主要从事光伏发电以及配电网重构方向的研究。
程若发(1971-),男,安徽六安人,教授,硕士研究生导师,主要从事微电网安全评估及其多目标优化方向的研究。
1671-4598(2017)11-0201-04
10.16526/j.cnki.11-4762/tp.2017.11.051
TP273
A

