圆锥形顶太阳能蓄热水箱锥顶结构及运行参数优化

王 烨，鲍成柯，付银安，王乐李



圆锥形顶太阳能蓄热水箱锥顶结构及运行参数优化

王 烨1,2，鲍成柯1，付银安1，王乐李1,2

（1. 兰州交通大学环境与市政工程学院，兰州 730070；2. 兰州交通大学铁道车辆热工教育部重点实验室，兰州 730070）

为获得顶部为圆锥形结构的太阳能蓄热水箱最优锥顶结构及运行参数，对水箱在有内置隔板情况下的10种锥顶结构进行了数值设计，结果表明：在给定流动参数条件下，锥顶角在173.1°~118.1°间变化对水箱内热分层影响效果相当，高温热水区域范围略有增大；对于锥顶高度为0.09 m、锥顶角为159.6°的最佳结构水箱，水箱出口附近高温热水区域范围随冷水入口流速增大逐渐缩小、随热水入口温度提高而增大，但提高热水入口温度对于高温热水区域范围的增大程度在较高冷水入口流速时要小于较低冷水入口流速时的情况；在其他流体参数不变的情况下，冷热水出口温差随冷水入口流速增大呈上升趋势，但当冷水入口流速增大到一定值时其对增大冷热水出口温差的贡献趋于平缓；在冷水入口流速较小时提高热水入口温度对于增大冷热水出口温差的贡献要略大于冷水入口流速较大时的情况。热水入口温度为333 K、冷水入口温度为303 K、热水入口流速为0.05 m/s、冷水入口流速为0.9 m/s组合而成的工况以及热水入口温度为343 K、冷水入口温度为303 K、热水入口流速为0.05 m/s、冷水入口流速为0.9 m/s组合而成的工况适合于“小流量大温差”的热用户运行模式；热水入口温度为333 K、冷水入口温度为303 K、热水入口流速为0.05 m/s、冷水入口流速为0.1 m/s组合而成的工况以及热水入口温度为343 K、冷水入口温度为303 K、热水入口流速为0.05 m/s、冷水入口流速为0.1 m/s组合而成的工况适合于热用户对热水供应量需求较大的情况。

太阳能；优化；温度；太阳能蓄热水箱；锥顶角；运行参数；热分层；数值模拟

0 引 言

太阳能蓄热水箱是太阳能应用系统中存储太阳能的重要设备，如何设计其结构、确定其运行参数对于克服太阳能“不稳定性和随机性”的缺点、提高太阳能利用效率非常关键[1-3]。关于蓄热水箱蓄热性能的研究，对于静态运行模式（流体无流出或流入），大多是关于封闭方腔或竖向封闭柱体内自然对流换热过程对热分层和蓄热能力的影响机制分析[4-14]；对于具有动态运行模式（有流体进出口），主要从水箱内置隔板[15]、进出口流速和温度[16-19]、进口形式[20-21]、流态[22-25]、水箱侧壁散热[26]、安装角[27-30]等方面进行探索。但这些研究只是针对特定外形结构的蓄热水箱展开的。文献[15]研究了封闭的蓄热水箱内层流自然对流换热条件下10种蓄热水箱外形对蓄热容量和热分层的影响，发现具有“尖角”外形结构可获得最好的热分层效果，其中的“尖角”外形结构就包括了具有圆锥形顶的蓄热水箱。为了获得动态运行模式下内置隔板对热分层的影响规律，文献[16]数值分析了竖向圆柱体水箱内分别设置12种不同形式隔板及隔板位置与水箱内部温度分层效果的关系，发现中心开孔的圆形隔板最有利于促成良好的温度分层，同时得到了“圆形隔板水平安置、内孔直径为0.2 m、隔板距底面0.04 m时热分层效果最佳”的结论。文献[15]虽然发现了具有“尖角”结构的圆锥形顶蓄热水箱在热分层效果方面的优势，但并没有得到动态运行模式下的规律。文献[16]针对的虽然是动态运行模式，但研究的则是平顶圆柱形蓄热水箱。在动态运行模式下关于锥顶角以及流动参数对水箱内热分层影响的研究，目前还未见报道。本文综合文献[15]及文献[16]的研究结论，构建与文献[16]中水箱柱体尺寸、隔板尺寸、冷热水进出口短管尺寸及位置完全相同的具有圆锥形顶的蓄热水箱，通过改变锥顶角及流体参数来获得最佳的蓄热水箱结构及运行参数。

1 物理模型和数学模型

1.1 物理模型

顶部为圆锥形结构的圆柱形蓄热水箱外形及各部分尺寸如图1所示。

冷热水进、出口短管直径均为0.02 m。内置隔板直径为1.0 m，板厚0.003 m，中心开孔直径为0.2 m，隔板距离水箱底面0.04 m。文献[16]中锥形顶至水箱底面总高度为150 mm，本文计算中由于锥顶角变化使得该尺寸在此基础上会有较小的变动。冷热水进、出口流向如图2所示。图中坐标原点与水箱底面圆心重合，轴垂直向上。

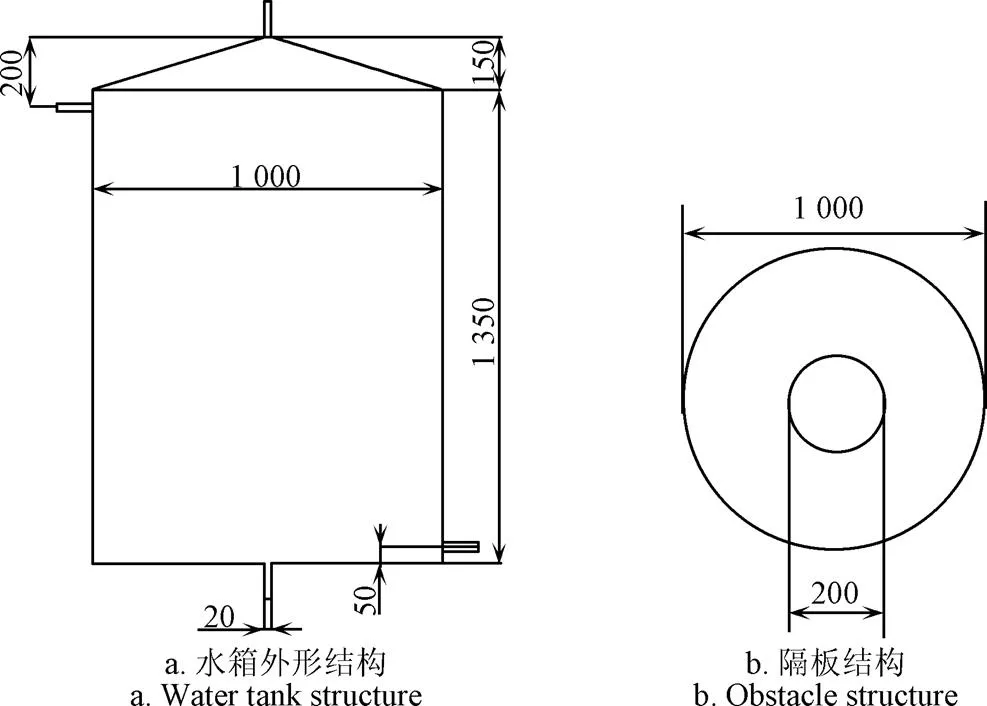
图1 水箱和隔板外形及尺寸

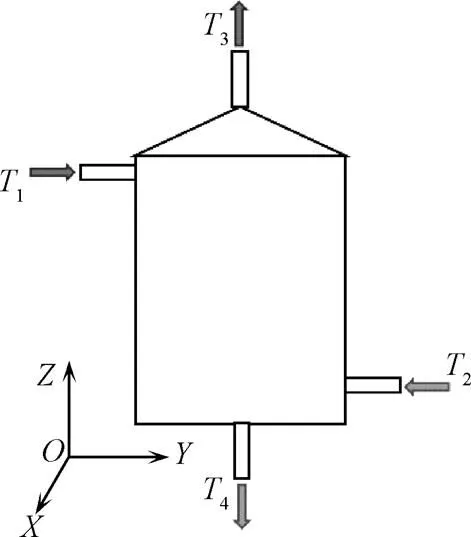
注：T1为来自集热器的热水入口温度；T2为来自用户端进入蓄热水箱的回水温度；T3为水箱热水出口温度；T4为回到集热器的冷水出口温度。

1.2 数学模型

在柱坐标系下采用标准模型对三维非稳态连续性方程、动量方程以及能量方程进行求解[16]。控制方程如下：

连续性方程：

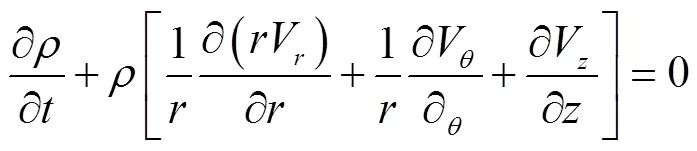
动量方程：

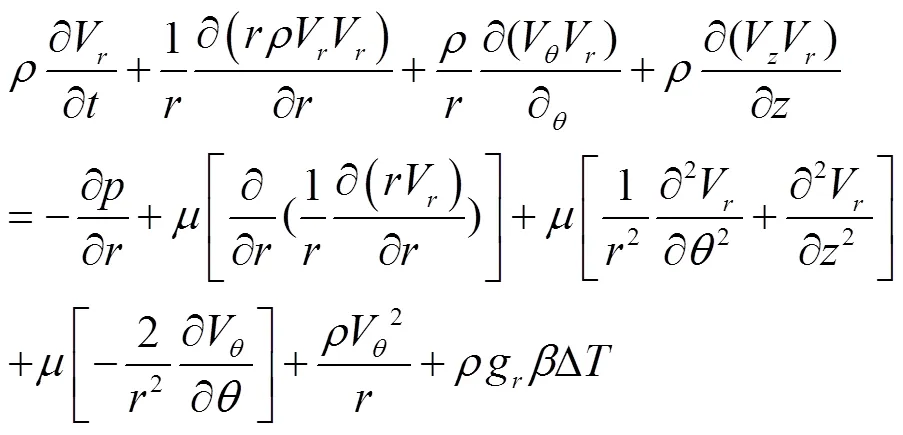
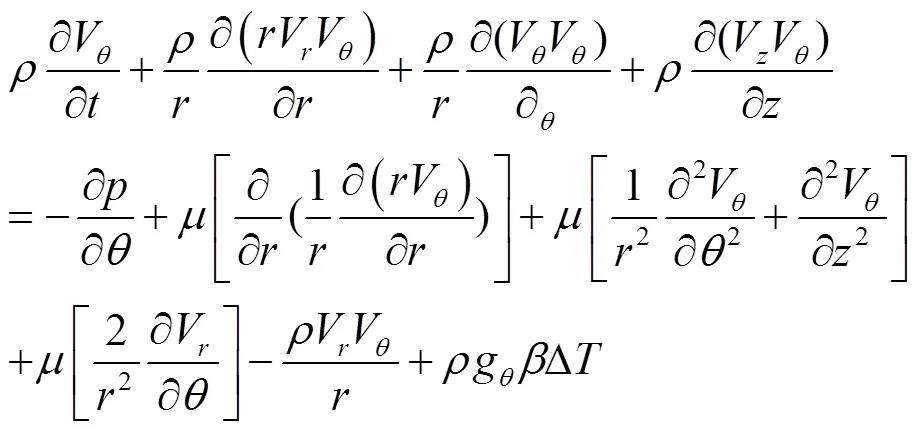
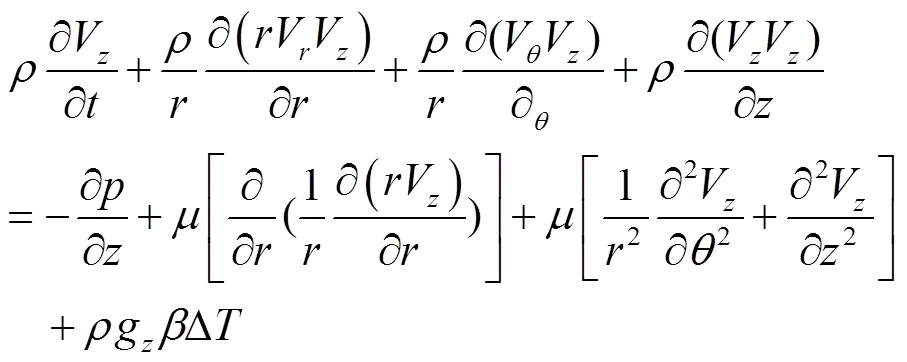
能量方程：

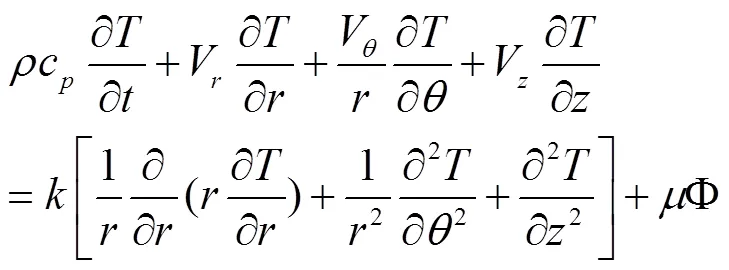
式中，和分别为，及向的速度，m/s；为温度，K；为动力黏度，（N·s）/m2；为密度，kg/m3；为体积膨胀系数，m3/K；为定压比热，J/(kg·K)；为传热系数，W/(m2·K)；为黏性扩散系数；，和分别为重力加速度在，和向的分量，m/s2。

流体为水，密度变化采用Boussinesq假设。

1.3 边界条件和初始条件

水箱内水的初始温度设为320 K，水箱中的压力为1 atm，冷、热水出口设为自由出流边界。水箱壁面和隔板壁面均为绝热边界条件和速度无滑移条件。

2 数值求解方法

2.1 数学模型验证

采用与文献[16]相同的数学模型及计算条件，并与文献[17]的试验数据进行比对，如图3所示。本文结果与文献[17]的试验结果间的相对偏差平均值为0.2%，是可以满足工程计算要求的。所以，本文1.2节的数学模型可作为后续的计算模型。

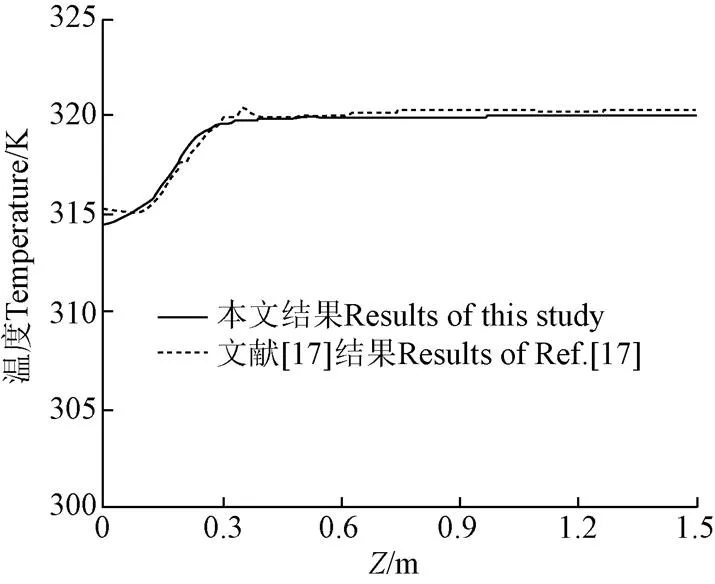
图3 水箱轴心沿Z轴正向温度曲线（300 s）

2.2 网格划分及独立性验证

采用gambit对水箱内计算区域进行离散，网格类型为T-Grid。以锥顶角为166.3°的水箱为研究对象，分别取热水入口温度为333 K，冷水入口温度为303 K，热水入口流速为0.05 m/s，冷水入口流速为0.5 m/s进行数值模拟，时间步长取0.25 s，计算时长取1 800 s，得到不同网格数下沿轴正向的温度分布，如图4所示。可以看出，三套网格的计算结果很接近，可以认为计算结果是网格独立的。考虑计算的经济性，后续计算选取网格数为424 377。

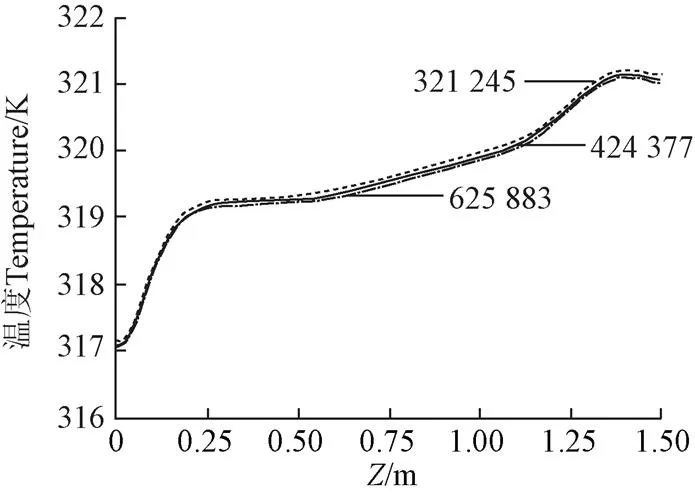
图4 网格独立性验证（图中数值为网格数）

2.3 时间步长确定

分别取时间步长为0.1、0.2、0.25 s，采用与2.2节相同的水箱结构及运行参数设置进行计算，得到水箱内沿轴正向的温度分布，如图5所示。可以看出，不同时间步长所得水箱内沿轴正向的温度分布曲线吻合度很好。考虑计算的耗时问题，后续计算中时间步长均取0.25 s。

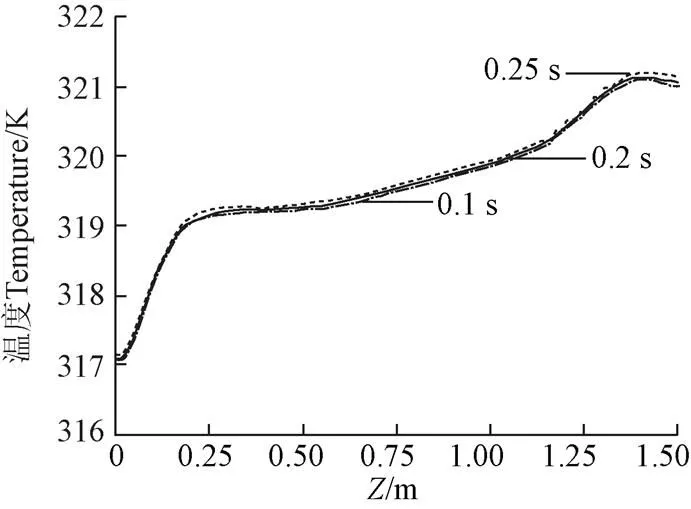
图5 不同时间步长下沿Z轴正向温度曲线

2.4 求解计算

采用非耦合隐式算法求解控制方程。离散格式为：压力项采用标准格式，动量方程、能量方程、湍流动能方程及湍流动能耗散率方程采用二阶迎风格式，采用SIMPLE算法求解速度和压力耦合问题[31]。松弛因子设置：压力为0.3，动量为0.7，湍流动能和湍流动能耗散率均为0.8，能量方程、动力黏度、体积力和密度均为1。湍流模型选用结合壁面函数法的标准模型。求解控制方程时的收敛条件与文献[32]相同，每个时层迭代20次，计算时长为1 800 s[16]。

3 计算结果及分析

3.1 锥顶尺寸影响分析

为了研究锥顶高度变化对水箱内热分层的影响，参考大量的文献报道数据：冷水入口流速取0.5 m/s，热水入口流速取0.05 m/s，冷水入口温度取303 K，热水入口温度取333 K。数值试验所取不同锥顶高度对应的水箱结构如表1所示。

若以文献[16]所取尺寸（即表1中5#水箱）对应容积为基准，表1中所列锥顶高度变化引起水箱容积的相对变化率在0.71%～3.57%之间。所以，后续分析中可以不考虑不同水箱由于液柱高差产生的静压差对热分层的影响以及容积不同所引起蓄热容量的微小差异。

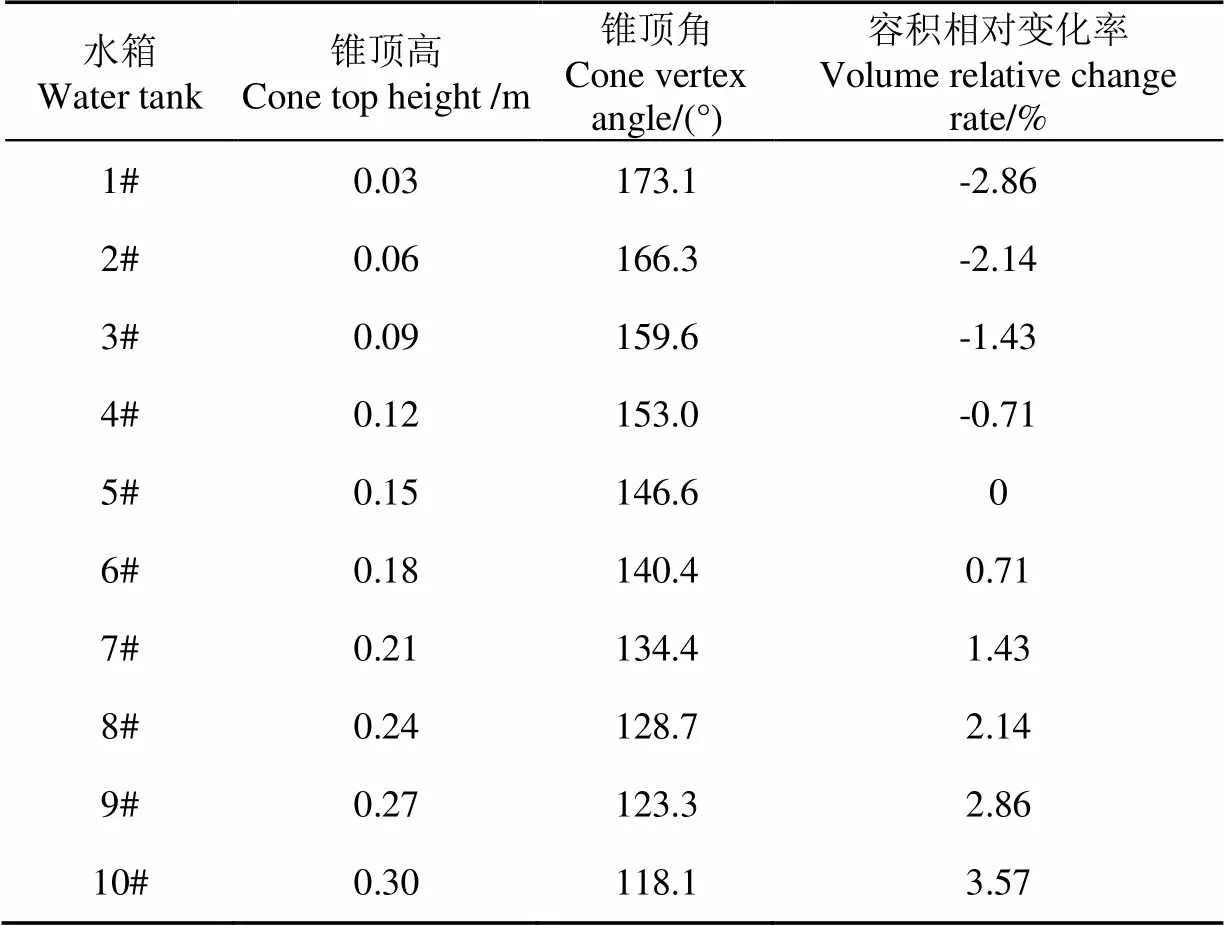
表1 锥形顶结构尺寸

图6为水箱内=0截面上的温度分布。可以看出，冷水经隔板中心孔以冲击流的形式进入隔板上部温度较高区域并与该区域热水进行热交换，形成了范围不同的低温区。但锥顶角在173.1°～118.1°之间变化的过程中，隔板上方形成的冲击流在温度场结构上差异很小，区域范围只有微小的减小；隔板下方区域的温度场也表现出了非常相近的结构。随着锥顶角的减小，锥顶附近高温热水区域范围略有增大。各水箱内隔板以上区域热分层效果相当。

图7为各水箱内部轴心沿方向上的温度分布比较。可以看出：各水箱在0.25～1.25 m之间的大部分区域内流体温度维持在320 K左右，近似为恒温流体区。在0～0.25 m之间水温变化剧烈，但各水箱除了在水箱底部温度有微小差异外，其余位置均保持了一致的温度水平。在1.25 m以上靠近水箱出口位置的区域，受圆锥体结构的影响，1#水箱温度最高，10#水箱温度最低，两者的差值在1.0 ℃以内，这与图6的分析结果一致。

图8为不同锥顶结构在=1 800 s时水箱冷热水出口温差比较。热水出口与冷水出口间温差越大越有利于获得较好的热分层效果，这也是评判蓄热水箱性能的重要指标之一[16]。由图8可知，3#水箱的热水与冷水出口温差最大，为10.98 K，10#水箱所得该温差最低，为9.8 K，1#水箱和2#水箱该温差与3#水箱接近，其余水箱冷热水出口温差均在10 K左右。这说明在相同的流动参数情况下，随着锥顶角在一定范围内逐渐减小，绝大部分水箱的冷热水出口温差呈现出逐渐减小的趋势，而3#水箱由于锥顶结构对流场的影响进而影响到温度场结构，使得冷热水出口温差达到了最大值。

综合不同锥顶结构对水箱内热分层及冷热水出口温度的影响分析，可以认为3#水箱为最佳的锥顶结构，确定为后续计算的物理模型。

3.2 运行参数影响分析

根据3.1节分析结果，3#水箱结构最优，下面针对该水箱结构，分析表2所示流动参数对热分层及冷热水出口温度的影响。

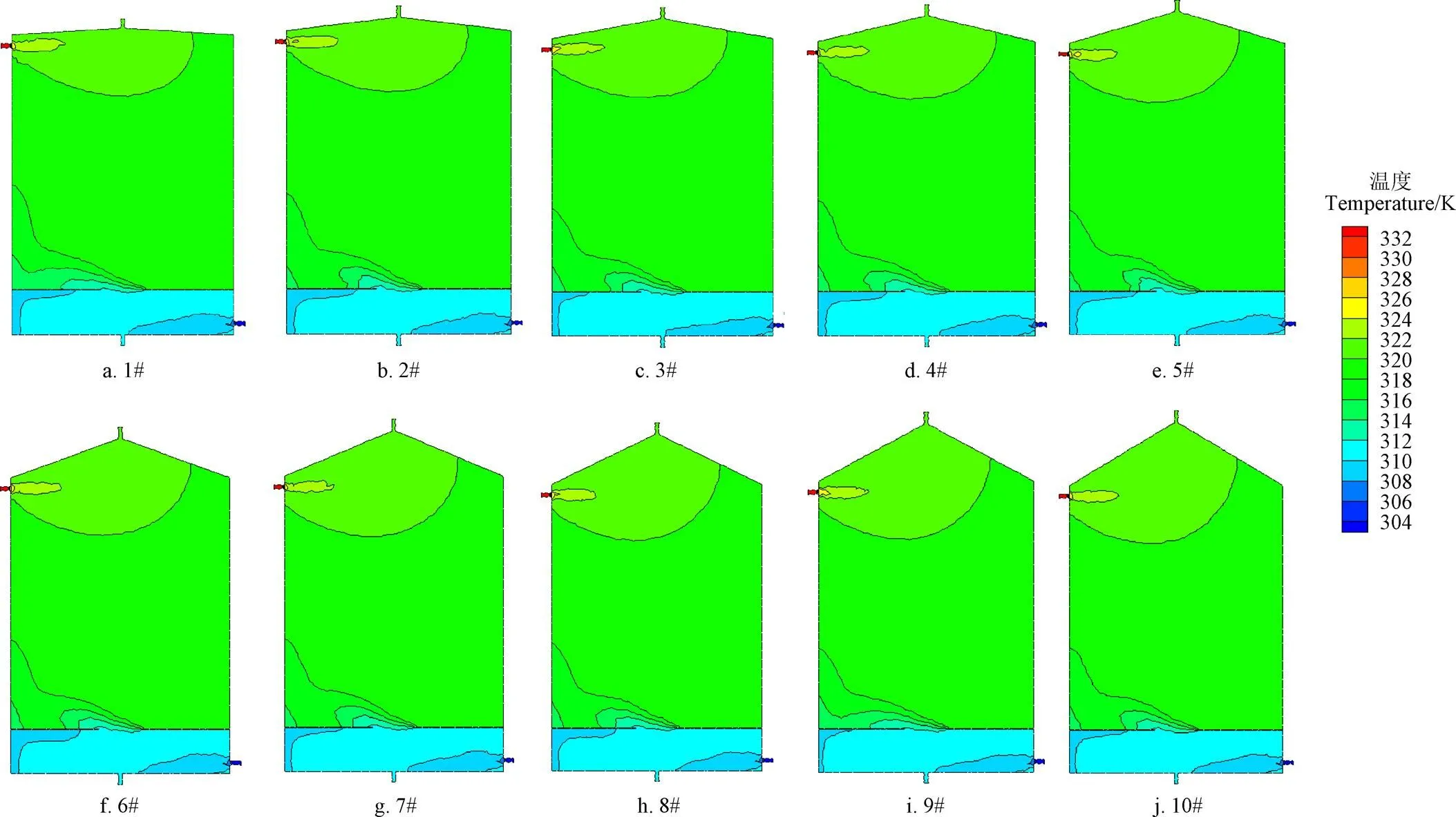
图6 各水箱X=0截面温度分布（1 800 s）

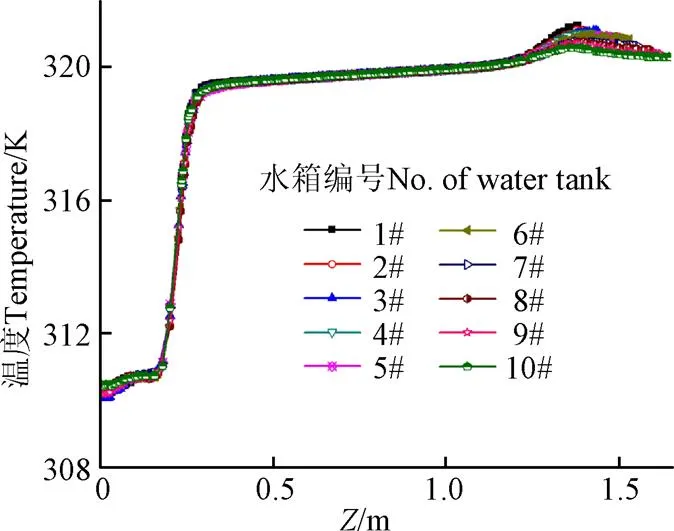
图7 各水箱沿Z轴正向温度曲线（1 800 s）

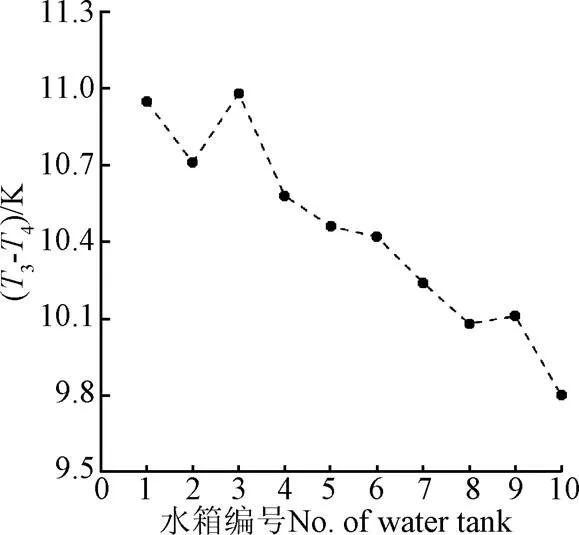
图8 不同水箱冷热水出口温差

图9为不同流体参数时=0截面上各工况的温度分布。工况1—5的1为333 K，由图9a-9e可以看出：在其他流体参数不变的情况下增大冷水入口流速，水箱出口附近高温热水区域范围逐渐缩小，冷水经隔板中心孔以冲击流的形式进入隔板上部温度较高区域并与该区域热水进行热交换，形成了范围逐渐扩大的低温区，使得水箱上部区域热分层遭到局部破坏，即水箱内冷热水混合区域在逐渐扩大。隔板以下部分水温随冷水入口流速增大而降低。自工况3开始，隔板下部左上角处形成了低温回流区，这是冷水流速增大所引起的惯性效应，工况5的低温流体几乎充满了隔板以下整个区域。工况6－10的1为343 K，=0截面上温度分布如图9f－9j所示。可以看出：在同一冷水入口流速条件下，热水入口温度增大，水箱出口附近热水区域范围有所扩展，温度梯度有小幅度增大，热分层效果有所改善。而且，较高冷水入口流速时这一热水区域范围增大的程度要小于较低冷水入口流速时的情况。所以，在较小的冷水入口流速运行情况下可以考虑通过提高热水入口温度来改善水箱顶部热分层状况。与1为333 K的对应工况比较，冷水经隔板中心孔在隔板上部形成的冲击流温度场向上稍有爬升，热水入口温度的变化对隔板下部温度场结构影响很微弱。

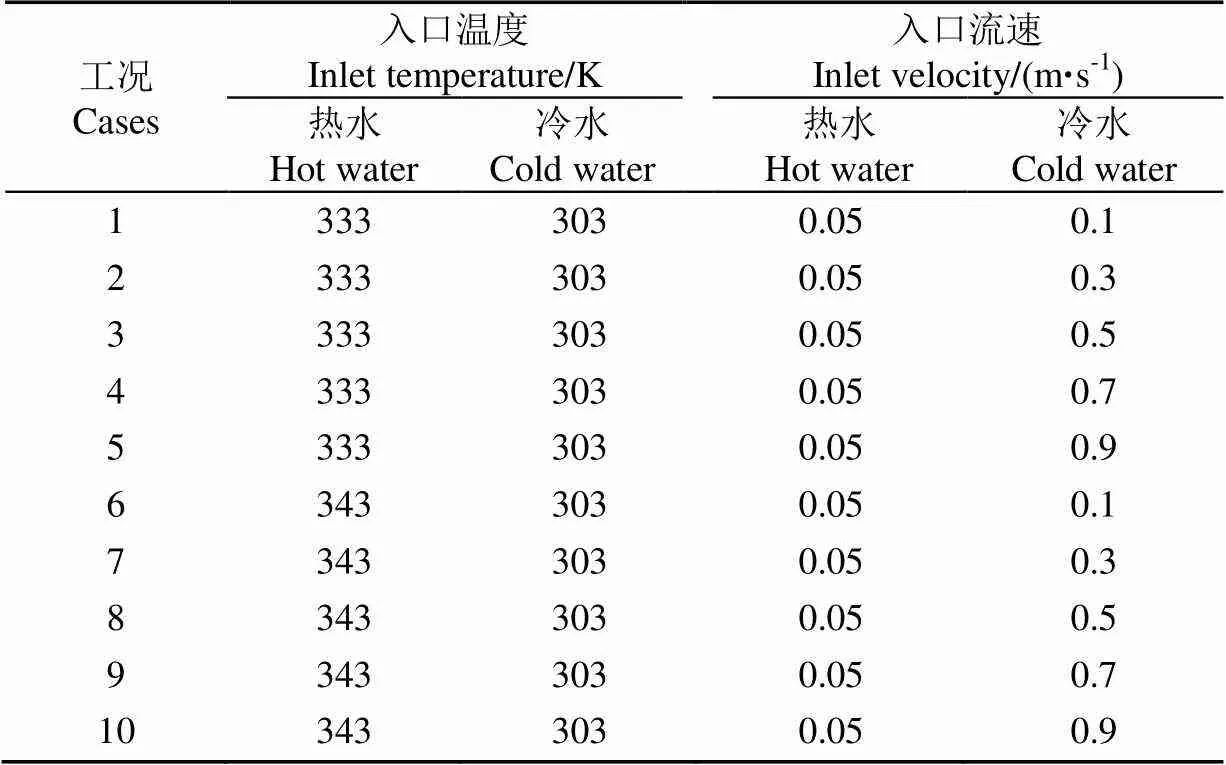
表2 模拟工况

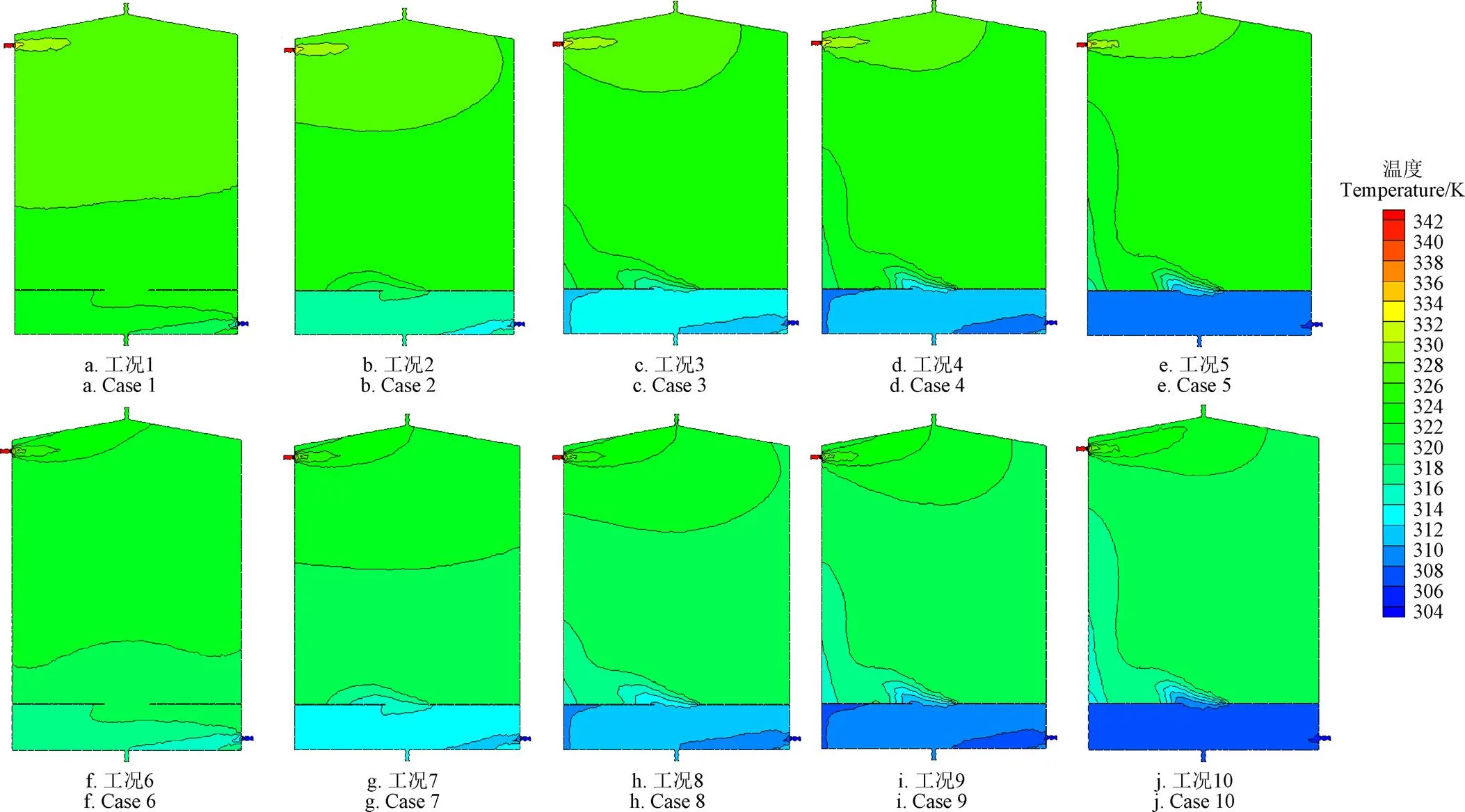
图9 不同工况下3#水箱在X=0截面温度分布（1 800 s）

以上现象表明：冷水入口流速增大会激励水箱内冷热水的掺混程度，但隔板的存在使得冷水入口流速增大时也增大了水箱顶部与底部间的流体温差，这对于改善水箱内热分层效果是有利的[16]，水箱底部流体温度降低也就降低了去集热器的冷水温度，有利于提高集热器效率。此外，冷水入口流速的增大对水箱顶部热分层不利且降低了顶部热水温度。工程实际中，尽可能调高(3-4)值、降低(1-3)和(4-2)的值，水箱内的热分层效果会更好。

图10为各计算工况下水箱内部沿轴正向上的温度分布。

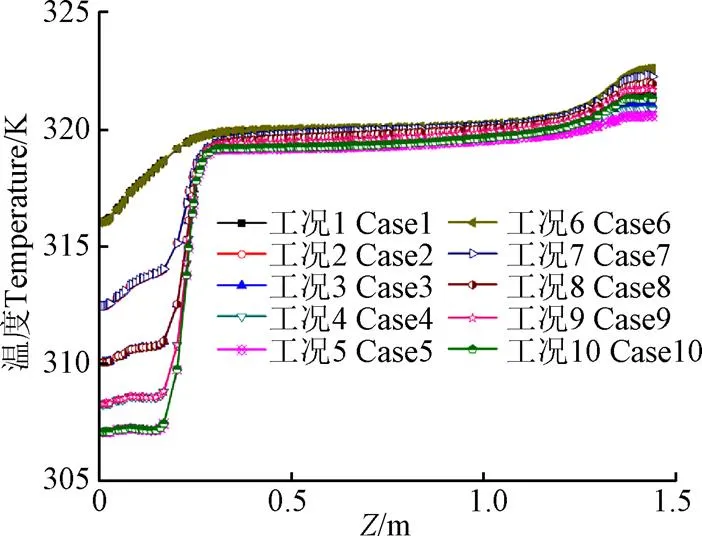
图10 各工况沿Z轴正向温度曲线（1800 s）

可以看出：各工况在0.3～1.3 m之间的大部分区域内流体温度维持在320 K左右，近似为恒温流体区。在0～0.3 m之间，水温受冷水入口流速影响显著，但不受热水入口温度影响，说明冷水入口流速对这一区域温度分布的影响较热水入口温度的影响更显著。另外，各工况对应水箱底部区域温度相差较大，其中工况1与工况6的水箱底部温度最高，均为316.03 K，工况5与工况10的水箱底部温度最低，均为307.08 K。各工况下水箱顶部温度相差较小，最高为工况6，为322.57 K，最低为工况5，为320.58 K。

图11为不同流动参数时（=1 800 s）水箱冷热水出口温差比较。可以看出，冷热水出口温差随冷水入口流速增大呈上升趋势，但当冷水入口流速增大到一定值时对增大冷热水出口温差的贡献趋于平缓。在冷水入口流速较小时提高热水入口温度对于增大冷热水出口温差的贡献要略大于冷水入口流速较大的情况，所以，在较小的冷水入口流速下提高热水入口温度是改善水箱热分层和提高供应热水温度的重要举措。从技术的角度，可以通过提高太阳能集热器集热效率来提高水箱热水入口温度，也可以通过改变热水利用循环系统的水泵工况点来增大来自热用户的回水流速，还可以同时实施这两个过程以提高冷热水出口温差。但冷水入口流速过大会破坏水箱隔板上方的热层稳定性。所以，在实际工程中，应综合太阳能集热器对回水的加热能力以及热用户对热水温度、流量的需求等对系统进行调试，以获得系统的最大热能利用效率。就本文所研究工况而言，工况5和工况10由于其高温水区域较小、蓄热容量较小、热分层稳定性较差，适合于“小流量大温差”的热用户运行模式；工况1和工况6由于具有较大的高温水区域、较小的冷热水出口温差，其蓄热容量较大、热分层稳定性好，适合于热用户对热水供应量需求较大的情况。

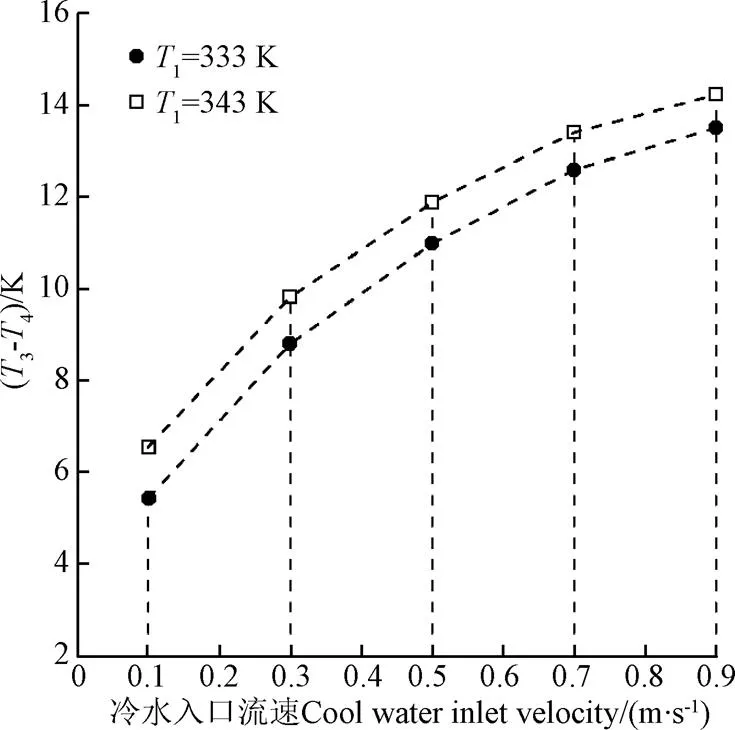
图11 冷水入口流速对出口温差的影响

4 结 论

分别讨论了圆锥形顶结构以及流动参数对具有圆锥形顶、内置隔板的蓄热水箱内热分层及热容量的影响，得到了如下主要结论：

1）在给定流动参数条件下，锥顶角从173.1°到118.1°的变化过程中，水箱内热分层效果相当，高温热水区域范围略有增大，锥顶高度为0.09 m、锥顶角为159.6°的水箱为最佳锥顶结构。

2）冷水入口流速对冷水出口温度影响明显，但对热水出口温度影响较小，水箱底部冷水出口及顶部热水出口的最高温度与最低温度间相差分别为8.95和1.99 K。

3）增大冷水入口流速会引起水箱顶部高温热水区域范围缩小；在同一冷水入口流速条件下，增大热水入口温度有助于水箱热容量的增大和热分层效果的改善，较高冷水入口流速时这一热水区域范围增大的程度要小于较低冷水入口流速时的情况。所以，在较小的冷水入口流速运行情况下可以考虑通过提高热水入口温度来改善水箱顶部热分层状况。

4）在其他流体参数不变的情况下，增大冷水流速及提高热水入口温度均有利于冷热水出口温差的提高，但冷水流速过大会破坏热分层的稳定性；在实际工程中尽可能在较小的冷水入口流速情况下提高热水入口温度来达到预期的热分层效果。

本文所得结论仅从“热分层效果”及“热容量”两个指标考虑，实际工程中，要提高整个太阳能系统的能效，还必须根据太阳能集热器类型、当地气象条件、热用户具体需求及运行模式等对蓄热水箱的运行参数进行合理调节。

[1] Zachár A, AszÓdi A. Numerical analysis of flow distributors to improve temperature stratification in storage tanks[J]. Numerical Heat Transfer, 2007, 51: 919－940.

[2] Kong L K, Yuan W X, Zhu N. CFD simulations of thermal stratification heat storage water tank with an inside cylinder with openings[J]. Procedia Engineering, 2016, 146: 394－399.

[3] Abdelhak O, Mhiri H, Bournot P. CFD analysis of thermal stratification in domestic hot water storage tank during dynamic mode[J]. Building Simulation, 2015, 8(4): 421－429.

[4] He Y L, Tao W Q, Qu Z G, et al. Steady natural convection in a vertical cylindrical envelope with adiabatic lateral wall[J]. International Journal of Heat Mass Transfer, 2004, 47: 3131－3144.

[5] Catton I, Edwards D K. Effect of side walls on natural convection between horizontal plates heated from below[J]. ASME Journal of Heat Transfer, 1967, 89(4): 295－299.

[6] Edwards D K, Catton I. Prediction of heat transfer by natural convection in closed cylinders heated from below[J]. International Journal of Heat Mass Transfer, 1969, 12(1): 25－30.

[7] Holzbecher M, Steiffs A. Laminar and turbulent free convection in vertical cylinders with internal heat generationt[J]. International Journal of Heat Mass Transfer, 1995, 38: 2893－2903.

[8] Papanicolaou E, Belessiotis V. Transient natural convection in a cylindrical enclosure at high Rayleigh numbers[J]. International Journal of Heat Mass Transfer, 2002, 45: 1425－1444.

[9] Oliveski R D C. Correlation for the cooling process of vertical storage tanks under natural convection for high Prandtl number[J]. International Journal of Heat Mass Transfer, 2013, 57: 292－298.

[10] Oliveski R D C, Krenzinager A, Vielmo H A. Cooling of cylindrical vertical tanks submitted to natural internal convection[J]. International Journal of Heat Mass Transfer, 2013, 46: 2015－2026.

[11] Davis G D V. Natural convection of air in a square cavity: A benchmark numerical solution[J]. International Journal of Numerical Methods Fluids, 1983, 3: 249－264.

[12] Mallison G, Davis G D V. Three-dimensional natural convection in a box: A numerical study, Journal of Fluid Mechanism, 1977, 83: 1－31.

[13] Vierendeels J, Merci B, Dick E. Numerical study of convective heat transfer with large temperature differences[J]. International Journal of Numerical Methods Heat Fluid Flow, 2001, 11: 329－341.

[14] Sharif M A, Mohammad T R. Natural convection in cavities with constant flux heating at the bottom wall and isothermal cooling from the sidewalls[J]. International Journal of Thermal Science, 2005, 44: 865－878.

[15] Yang Z, Chen H S, Wang L, et al. Comparative study of the influences of different water tank shapes on thermal energy storage capacity and thermal stratification[J]. Renewable Energy, 2016, 85: 31－44.

[16] Altuntop N, Arslan M, Ozceyhan V, et al. Effect of obstacles on thermal stratification in hot water storage tanks[J]. Applied Thermal Engineering, 2005, 25: 2285－2298.

[17] Zachar A, Farkas I, Szlivka F. Numerical analyses of the impact of plates for thermal stratification inside a storage tank with upper and lower inlet flows[J]. Solar Energy, 2003, 74: 287－302.

[18] 薛英霞，徐晨辉. 太阳能采暖水箱温度分层的仿真分析[J]. 建筑热能通风空调，2014，33(2)：58－60.

Xue Yingxia, Xu Chenhui. Analysis and simulation on temperature stratification of heat storage tank in solar heating system[J]. Building Energy & Environment, 2014, 33(2): 58－60. (in Chinese with English abstract)

[19] Gao W F, Liu T, Lin W X, et al. Numerical study on mixing characteristics of hot water inside the storage tank of a solar system with different inlet velocities of the supply cold water[J]. Procedia Environmental Sciences, 2011, 11: 1153－1163.

[20] 李舒宏，李阳，张小松，等. 新型进水口结构对储能水箱释能性能的影响[J]. 中南大学学报：自然科学版，2012，43(10)：4068－4074.

Li Shuhong, Li Yang, Zhang Xiaosong, et al. Effect of new-type inlet structures on discharging performance of storage tank[J]. Journal of Central South University: Science and Technology, 2012, 43(10): 4068－4074. (in Chinese with English abstract)

[21] Louise J S, Simon F. Entrance effects in solar storage tanks[J]. Solar Energy, 2003, 75(4): 337－348.

[22] Vliet G C, Liu C K. An experimental study of turbulent natural convection boundary layers[J]. Journal of Heat Transfer, 1969, 91: 517－531.

[23] Sparrow E M, Gregg J L. Laminar free convection from a vertical plate with uniform surface heat flux[J]. Journal of Heat Transfer, 1956, 78: 435－440.

[24] Bejan A, Large J L. The Prandtl number effect on the transition in natural convection along a vertical surface[J]. Journal of Heat Transfer, 1990, 112: 789－790.

[25] Popiel C O. Free convection heat transfer from vertical slender cylinders: A review[J]. Heat Transfer Engineering, 2008, 29 (6): 521－536.

[26] Rosen M A. Effect of stratification on energy and exergy capacities in thermal storage systems[J]. International Journal of Energy Resource, 2004, 28(2): 177－193.

[27] Oshchepkov M Y, Frid S E. Thermal stratification in storage tanks of integrated collector storage solar water heaters[J]. Applied Solar Energy, 2015, 51(1): 74－82.

[28] Junaidi H A, Henderson D, Muneer T, et al. Study of stratification in a (ICSSWH) Integrated Collector Storage Solar Water Heater[C]// Proc 9th AIAA ASME Joint Conf, San Francisco, CA, June 5–8, 2006.

[29] Henderson D, Junaidi H, Muneer T, et al. Experimental and CFD investigation of an ICSSWH at various inclinations[J]. Renewable & Sustainable Energy Reviews, 2007, 11 (6): 1087－1116.

[30] Polyakov A F, Frid S E. Numerical simulation of temperature stratification in accumulation solar water heater[J]. High Temperature, 2014, 52 (3): 417-423.

[31] 陶文铨. 数值传热学[M]. 第二版. 西安：西安交通大学出版社，2001.

[32] 王烨，徐燃. 青藏线空调列车室内气流组织的沿线变化数值分析[J]. 重庆大学学报，2014，37(9)：59－67.

Wang Ye, Xu Ran. Numerical study of airflow distribution in air-conditioned train in Qinghai-Tibet Railway[J]. Journal of Chongqing University, 2014, 37(9): 59－67. (in Chinese with English abstract)

王 烨，鲍成柯，付银安，王乐李. 圆锥形顶太阳能蓄热水箱锥顶结构及运行参数优化[J]. 农业工程学报，2017，33(22)：255－261. doi：10.11975/j.issn.1002-6819.2017.22.033 http://www.tcsae.org

Wang Ye, Bao Chengke, Fu Yin’an, Wang Leli. Structure and operating parameter optimization of solar hot water storage tank with conical top[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(22): 255－261. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.22.033 http://www.tcsae.org

Study of structure optimization of solar hot water storage tank with conical top

Wang Ye1,2, Bao Chengke1, Fu Yin’an1, Wang Leli1,2

(1.730070,; 2.730070,)

Solar hot water storage tank is one of the key thermal storage equipment of the solar energy system and it has significant effect on the reliability of thermal energy supply. For the solar hot water storage tank, its optimal structure and reasonable fluid parameters are very important for improving the solar energy system efficiency. Published references indicate that the hot water storage tank with conical top has better performance than the hot water storage tank with plane top. But there is no study about the relationships among the cone vertex angles, fluid parameters and the thermal stratification effect for the hot water storage tank with conical top. This paper mainly aims to obtain the optimal structure of the solar hot water storage tank with conical top and the operating parameters. The standardmodel was adopted to analyze the influence of cone vertex angle and operating parameters on the thermal stratification of the hot water storage tank with conical top. The results show that the studied cone vertex angles have a little effect on thermal stratification and the hot water region slightly expands with the decreasing of cone vertex angle. In terms of the optimal water storage tank with the conical top height of 0.09 m and cone vertex angle of 159.6°, the hot water region is reduced with the increasing of cold water inlet velocity and the decreasing of hot water inlet temperature. However, higher hot water inlet temperature has less effect on the hot water region on condition of higher cold water inlet velocity than that of lower cold water inlet velocity. Thus, in practical engineering operation, to improve hot water inlet temperature under lower cold water inlet velocity can obtain better thermal stratification effect. For given fluid parameters, the difference between the hot water outlet temperature and cold water outlet temperature increases with the increasing of cold water inlet velocity. Increasing hot water inlet temperature under lower cold water inlet velocity makes a slightly larger contribution to improving the difference between the hot water outlet temperature and the cold water outlet temperature. To improve hot water inlet temperature from 333 to 343 K has no effect on the cold water outlet temperature in this study. One case with hot water inlet temperature of 333 K, cold water inlet temperature of 303 K, hot water inlet velocity of 0.05 m/s and cold water inlet velocity of 0.9 m/s and the other case with hot water inlet temperature of 343 K, cold water inlet temperature of 303 K, hot water inlet velocity of 0.05 m/s and cold water inlet velocity of 0.9 m/s are suitable to the running mode of “low flow flux and high temperature difference”. One case with hot water inlet temperature of 333 K, cold water inlet temperature of 303 K, hot water inlet velocity of 0.05 m/s and cold water inlet velocity of 0.1 m/s and the other case with hot water inlet temperature of 343 K, cold water inlet temperature of 303 K, hot water inlet velocity of 0.05 m/s and cold water inlet velocity of 0.1 m/s are suitable for the users with large demand for hot water supply. In order to obtain high efficiency of solar energy system in practical engineering, many factors, such as types of solar collectors, local weather conditions, specific requirements of thermal users and operation modes must be considered simultaneously.

solar energy; optimization; temperature; solar hot water storage tank; cone vertex angle; operating parameters; thermal stratification; numerical simulation

10.11975/j.issn.1002-6819.2017.22.033

TU822

A

1002-6819(2017)-22-0255-07

2017-07-07

2017-10-01

国家自然科学基金资助项目（51476073, 51266004）；甘肃省建设科技攻关项目（JK2016-2）

王 烨，男，甘肃宁县人，教授，博士，博士生导师。主要从事自然对流及暖通空调研究。Email：wangye@mail.lzjtu.cn