协同制导防空中JTC和FrFT纯相位加密技术
,,
(1.中国人民解放军92941部队,辽宁 葫芦岛 125000; 2.中国人民解放军91899部队,辽宁 葫芦岛 125000)
协同制导防空中JTC和FrFT纯相位加密技术
宋洁1,孙彦星2,魏全超2
(1.中国人民解放军92941部队,辽宁葫芦岛125000; 2.中国人民解放军91899部队,辽宁葫芦岛125000)
为了满足协同制导防空作战时,编队内各舰艇之间火控级的信息共享及数据传输,对协同制导防空作战通信时,在信息传输过程中可能用到的新技术,提出了基于联合变换相关器(joint transform correlator, JTC)和分数傅里叶变换(fractional Fourier transform, FrFT )的纯相位图像加密方法;加密时,首先将原始图像置乱后编码为相位函数,与相位掩膜相乘后和密钥分别放入联合变换相关器输入平面,成为待加密函数,经过α阶联合分数傅里叶透镜后在输出平面获得密文;解密时,先将密钥放在输入端,经过α阶分数傅里叶变换后与密文相乘,再经过-α阶联合分数傅里叶变换后得到包含原始图像的解密信息,提取其相位,经过反置乱后得到解密图像;数值仿真结果表明,该方法对密钥响应敏感,并有效地提高了解密图像质量、系统的安全性能和抗干扰能力。
协同制导防空作战;光学图像加密;纯相位编码;联合变换相关器;分数傅里叶变换
0 引言
协同制导防空作战是一项复杂的系统工程,涉及探测、通信、导弹制导、作战指挥和控制等多个领域。根据协同制导作战流程,需要研究的技术包括数据共享、导弹制导和作战使用等。数据信息的共享要满足数据传输的可靠性和时空一致性,无论是对来袭目标的跟踪还是对舰空导弹的跟踪制导,都要求编队内数据传输具有很高的可靠性[1]。数据传输可能也包含图像信息的传输,图像加密技术就可能成为协同制导防空作战在通信过程中要面临的新技术,对图像加密技术的深入研究,有助于更好的完成协同制导防空作战中信息的共享和传输。
自从1995年,Refregier 和Javidi等人提出了基于4f系统的双随机相位编码技术[2],基于光学原理的图像信息处理技术得到了快速发展。为了增加双随机相位的安全性能,先后有人提出了基于菲涅尔变换的双随机相位编码技术[3]、基于分数傅里叶变换的双随机相位编码技术[4-6]、基于数字全息[7-8]的随机相位编码技术。基于4f系统的双随机相位编码加密技术虽然结构简单,安全性高,但对空间排列精度要求高,解密时需要制作复共轭的相位掩膜,且密文不能直接打印和输出等,实用性较差。为了解决上述问题,Nomura等提出了在傅里叶域利用联合变换相关器(Joint Transform Correlator, JTC)[9-10]的光学图像加密方法。该方法在JTC加密系统中设置两个输入窗口面,其中一个重叠放置待加密图像和随机相位掩膜,另一个独立放置作为密钥的随机相位掩膜,作为密钥的随机相位掩膜可通过一块毛玻璃实现,其在输入面的移动只是改变解密图像的相对位置,而对解密图像质量没有任何影响,同时以联合变换功率谱形式输出的加密图像可直接打印,解密过程也无需制作复共轭密钥。为了提高密钥空间,Vilardy J M[11]等将JTC加密技术拓展到分数傅里叶变换,但解密图像质量差,且噪声严重。随后,他们提出了两种改进方法[12-13]:一种是对JTC结构进行非线性校正,另一种是去除分数傅里叶域的零级项,大大地提高了分数傅里叶域JTC加密系统的解密图像质量。但是针对基于JTC图像加密系统的攻击方法,择性明文攻击、已知明文攻击、唯密文攻击,也相继提出。本文将原始图像先进行像素置乱,再经过空间光调制器,将置乱后的原始图像编码成纯相位图像,再结合JTC和FrFT技术,提高图像的安全性能、解密质量和抗干扰能力。
1 基于联合变换相关器和分数傅里叶变换的相位编码图像加密方法
1.1 加密原理
加密过程如图1所示,设f(x,y)为待加密图像归一化后的函数表达式,r(x,y)和h(x,y)为两个随机相位,表达式为:

图1 加密原理
(1)
式(1)中s(x,y)和n(x,y)为[0,1]区间内生成的随机数。如图1(a)所示,归一化处理后的原始图像f(x,y)经过像素置乱变为J(f(x,y)),再通过光调制器编码成纯相位函数p(x,y)=exp{iπJ[f(x,y)]},与相位掩膜相乘生成函数g(x,y),g(x,y)=p(x,y)r(x,y)。将得到的g(x,y)和密钥h(x,y)分别放在输入平面(x=a,y=b),(x=-a,y=-b)处如图1(a)所示,得到输入平面函数为:
in(x,y)=g(x-a,y-b)+h(x+a,y+b)
(2)
对输入平面照射平行光,经过阶数为α的透镜1后得到:
IN(u,v)=Fα(in(x,y))=
Fα(g(x-a,y-b)+h(x+a,y+b))=
(3)
其中:透镜1为阶数为α阶分数傅里叶变换透镜,变量(x,y)由空域变换到分数傅里叶域的变量(u,v),u0=u-acosα,v0=v-bcosα;u1=u+acosα,v1=v+bcosα。
在输出平面用CCD得到输入信号的功率谱密度,即:
E(u,v)=|IN(u,v)|2=|G(u0,v0)|2+|H(u0,v0)|2+
G*(u0,v0)×H(u1,v1)exp(j2ausinα)exp(j2bvsinα)+
G(u0,v0)×H*(u1,v1)exp(-j2ausinα)exp(-j2bvsinα)
(4)
联合相关器得到的联合功率谱分布中,不仅包含两个函数的相关项,还存在零级项,即式中第一项和第二项,且这两项常常比相关项高出好几倍,严重影响解密图像的质量,所以需对去除零级像。去除的方法是单独将原始图像g(x)放在输入平面x=a,y=b,经过α阶二维分数傅里叶变换后得到功率谱分布|G(u0,v0)|2;再单独将密钥h(x)放在输入平面x=-a,y=-b上经过α阶分数傅里叶变换后得到|H(u1,v1)|2。去除零级项后的密文为:
E1(u,v)=E(u,v)-|G(u0,v0)|2-|H(u1,v1)|2=
G*(u0,v0)×H(u1,v1)exp(j2ausinα)exp(j2bvsinα)+
G(u0,v0)×H*(u1,v1)exp(-j2ausinα)exp(-j2bvsinα)
(5)
JTC加密系统中密钥模板由于面积有限,实为一截断相位函数,其分数傅里叶变换后也不是一个纯相位函数,造成解密后的图像为原始图像与密钥的卷积,无法恢复原始图像。为有效解密原始图像,可对去除零级项后的密文除以密钥的分数傅里叶变换功率谱|H(u1,v1)|2,从而得到加密后的密文最终表达式为:
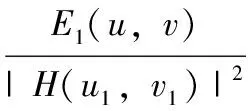

(6)
1.2 解密原理
图像解密过程如图2所示,在图2(a)中,密钥h(x)放在输入平面(x=-a,y=-b)上,对输入平面照射平行光,经过透镜1在分数傅里叶频谱平面得到:
H(u,v)=Fα(h(x+a,y+b))=H(u1,v1)
(7)
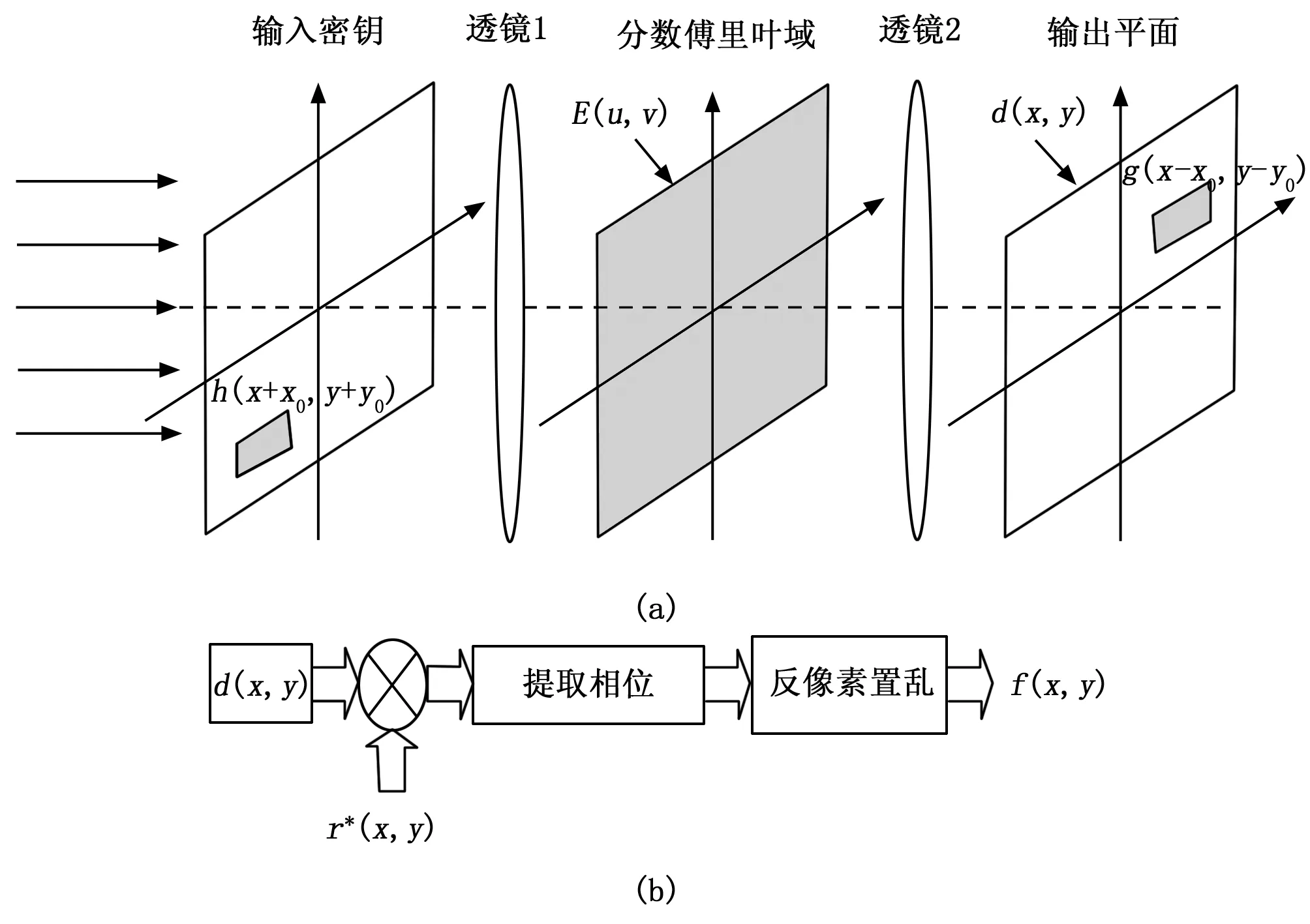
图2 解密原理
进而与放置于傅里叶变换平面的密文重叠并相乘,得到:
D(u,v)=E2(u,v)×H(u,v)=



(8)
再经过阶数为-α的分数傅里叶透镜2,得到:
d(x,y)=F-α(D(u,v))=
+g(x-a,y-b)
(9)
这样在输出平面(x=a,y=-b)处得到g(x),再与另一密钥的共轭相乘如图2(b),得到:
G(x,y)=g(x,y)×r*(x,y)=exp{iπJ[f(x,y)]}r(x,y)×
r*(x,y)=exp{iπJ[f(x,y)]}
(10)
提取G(x,y)的相位分布,再经过反置乱,即可得到解密图像f(x,y)。
由加解密过程可知,本文密钥有三部分组成:相位掩膜r(x)、系统密钥h(x)、分数傅里叶变换的分数阶参数。
2 仿真实验及性能分析
本文采用像素为256×256的lena图作为原始图像,输入平面大小为1792×1792,分数傅里叶变换阶数α=0.68,使用软件Matlab2014对系统的加解密过程进行仿真。用原始图像与解密图像的均方根误差(Root Mean Square Error, RMSE)客观评价加密算法的可靠性,数学定义如下:
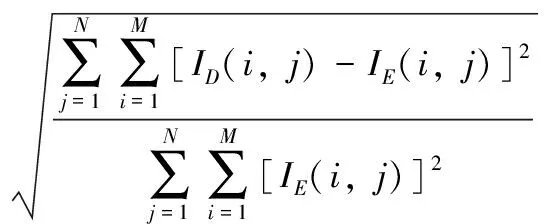
(11)
式中,IE(i,j),ID(i,j)表示原始图像和解密图像在(i,j)处的像素灰度值,M×N表示图像像素点数。设定均方根误差为0.4时作为判别阈值,只有当均方根小于此值时,图像可以恢复出来,大于此值便无法恢复。
2.1 原理仿真
图3为加密过程仿真图,其中,图3(a)为原始Lena图像;图3(b)原始图像的置乱,可见经过像素置乱,图像像素被打乱无法分辨;图3(c)是图像置乱后又经过相位编码生成的p(x,y);图3(d)是JTC系统的输入平面,在平面(x=a,y=b)处放置的是p(x,y)与随机掩膜r(x,y)相乘后生成的g(x),在(x=-a,y=-b)处放置的是密钥h(x);图3(e)是去除噪声和零级项后的密文。

图3 加密过程
图4为解密过程仿真图,其中图4(a)为图像解密时,将密钥h(x)放在输入平面(x=-a,y=-b)处;图4(b)表示密钥h(x)经过阶数为0.68的分数傅里叶透镜后与密文相乘,再经过阶数为-0.68的分数傅里叶透镜后在输出平面得到的输出图像;图4(c)是最后得到的解密图像,RMSE=0.012 4,从图中可以看出,解密图像质量高,几乎无失真;图4(d)和(e)分别为使用错误密钥h(x)和r(x)时得到的解密图像,均方根误差分别为0.645和0.640,从图中可以看出,使用错误密钥解密时,均得不到原始图像。

图4 解密过程
2.2 分数傅里叶变换的阶数分析
将傅里叶变换扩展到分数傅里叶变换为优点是分数傅里叶变换阶可变,加大了密钥空间,现对分数阶参数进行分析,假设两个密钥全部正确,当分数阶参数变化时,对解密图像的影响。图5(a)显示了均方根误差RMSE随不同分数阶参数偏移量变化的曲线图,图中取偏移量变化范围为(-0.5,0.5),从图中可以看出,当阶数偏移量为0时,RMSE急剧收敛,当分数阶偏移量大于0.002时,均方根误差值大于0.4。可见,由分数阶参数作为加密算法的主控密钥具有很高的敏感性,从而提高了加密系统的安全性能。
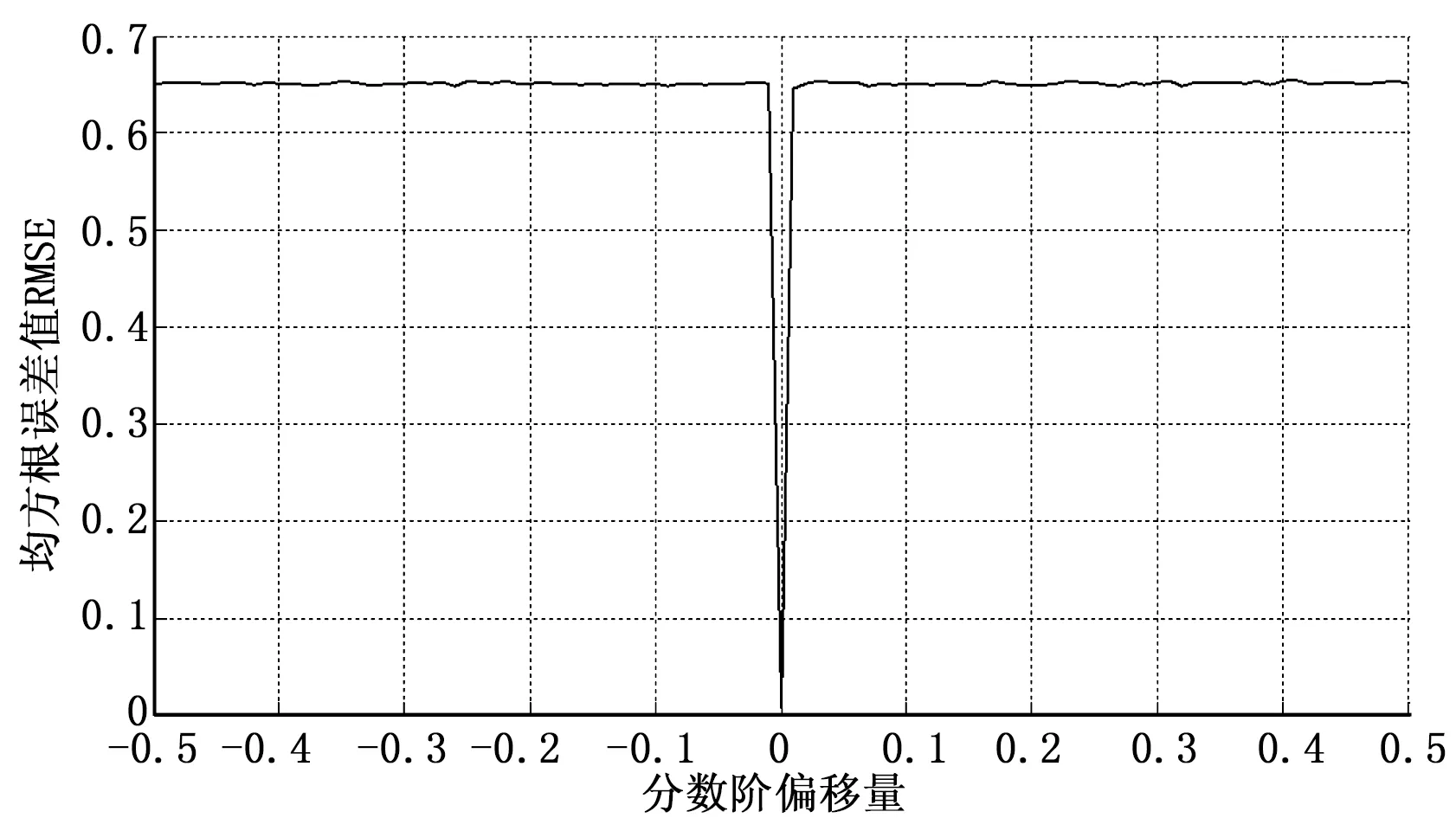
图5 分数傅里叶变换分数阶参数分析
2.3 抗剪切和抗噪声性能分析
对本文系统进行抗剪切和抗噪声性能分析,如图6所示,图6(a)表示剪切12.5%后的密文;图6(b)表示剪切25%后的密文;图6(c)表示剪切12.5%密文后的解密图像,RMSE=0.154;图6(d)表示剪切25%密文后的解密图像RMSE=0.251;图6(e)对密文添加均值为0,方差为0.2的高斯白噪声后的解密图像,RMSE=0.194;图6(f)为添加方差为0.2的噪声后再剪切12.5%后的解密图像,RMSE=0.264。以上几种鲁棒性实验,都可清晰的识别出原始图像,可见该算法具有很好的抗剪切和抗噪声性能。

图6 本文系统抗剪切和抗噪声性能分析
2.4 性能对比
为说明本系统的优越性,对原始图像只进行像素置乱,不进行相位编码,仿真结果如图7所示。图7(a)表示未经相位编码的解密图像,RMSE=0.021;图7(b)和(c)分别表示表示解切12.5%和剪切25%的密文后的解密图像, RMSE分别为0.233和0.489,图7(d)表示对密文添加零均值方差为0.2的高斯噪声后的解密图像,RMSE=0.376。表1表示与本文系统进行对比:

图7 未进行相位编码的仿真结果
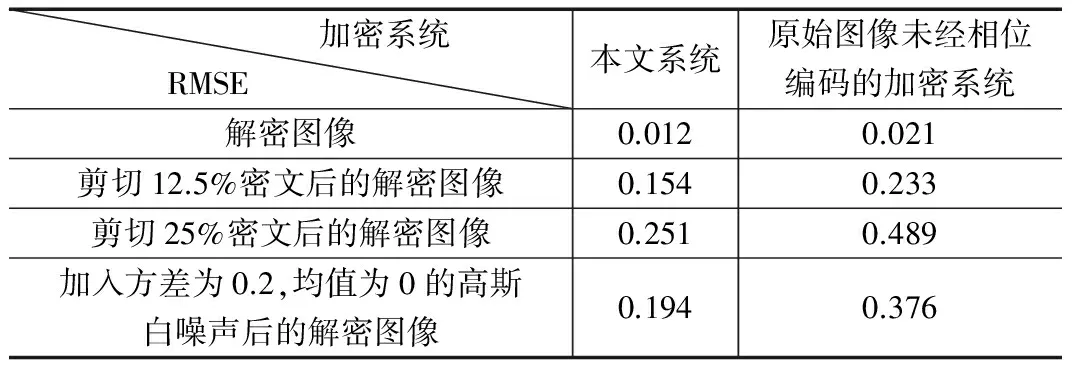
表1
从表1可以看出,将原始图像由振幅函数编码为相位函数,不仅可以提高解密图像质量,还提高了加密系统的抗剪切和抗噪声能力。
3 结论
提出了协同制导防空作战通信过程中可能用到的新技术,基于联合变换相关器和分数傅里叶变换技术的相位编码图像加密技术,并对此系统进行了仿真验证。利用JTC的图像加密技术使得密文可以直接输出;将分数傅里叶变换的分数阶参数作为加密系统的主控密钥,扩展了密钥宽度,增加了安全性能;将原始图像由振幅编码为相位,提高了解密图像的质量和系统的抗剪切和抗噪声能力。
[1] 秦剑冬,邢昌风,吴 玲. 编队舰空导弹协同制导防空作战研究[J]. 舰船科学技术,2010(5):80-83.
[2] Refregier P, Javidi B. Optical image encryption based on input plane and Fourier plane random encoding [J]. Optics letters, 1995, 20(7): 767-769.
[3]Matoba O, Javidi B. Encrypted optical memory system using three-dimensional keys in the Fresnel domain [J]. Optics letters ,1999,24(11), 762-764.
[4] Situ G, Zhang J. Double random-phase encoding in the Fresnel domain[J]. Optics Letters, 2004, 29(14): 1584-1586.
[5] Unnikrishnan G, Joseph J, Singh K. Optical encryption by double-random phase encoding in the fractional Fourier domain[J]. Optics Letters, 2000, 25(12): 887-889.
[6] Liu Shutian, Mi Quanlin, Zhu Banghe. Optical image encryption with multistage and multichannel fractional Fourier-domain filtering[J]. Optics Letters, 2001,26(16), 1242-1244.
[7] Hennelly B, Sheridan J. Image encryption and the fractional Fourier transform [J]. Optik-international Journal for Light and Electron Optics, 2003, 114(6): 251-265.
[8] Nishchal N K, Joseph J, Singh K. Fully phase-encrypted memory using cascaded extended fractional Fourier transform[J]. Optics and lasers in engineering, 2004, 42(2): 141-151.
[9] Tajahuerce E, Javidi B. Encryption three-dimensional information with digital holography [J]. Applied Optics, 2000, 39(35): 6595-6601.
[10] Javidi B, Nomura T. Securing information by use of digital holography [J]. Optical Letters, 2000,25(1):28-30.
[11] Wang B, Sun C C, Su W C, et al. Shift-tolerance property of an optical double-random phase-encoding encryption system[J]. Applied optics, 2000, 39(26): 4788-4793.
[12] Javidi B, Sergent A, Zhang G, et al. Fault tolerance properties of a double phase encoding encryption technique[J]. Optical Engineering, 1997, 36(4): 992-998.
[13] Nomura T and Javidi B. Optical encryption using a joint transform correlator architecture [J]. Opt. Eng, 2000,39:2031-2035.
FullyPhaseEncryptionUsingtheJointTransformCorrelatorandFractionalFourierTransforminAir-defenseCombatoftheCooperativeControlandGuidance
Song Jie1, Sun Yanxing2,Wei Quanchao2
(1.92941 Army,Huludao 125000,China; 2.91899 Army,Huludao 125000,China)
In order to realize the fire control information sharing and data transmission among the war ships during the air-defense combat of the cooperative control and guidance, for the newtechnology that may be used in the air-defense combat of the cooperative control and guidance , a phase image encryption method based on the joint transform correlator (JTC) and fractional Fourier transform (FrFT) is proposed. The original image is encoded into phase function after being scrambled, as the input signal. The encryption system based on JTC enlarged the key space and enhances the security, from Fourier domain to fractional Fourier domain by using fractional Fourier operators. The original image can be retrieved by using the correct key, the correct fractional order and pixel scrambling operators. The feasibility of the proposed encryption method is proved by numerical simulations.
air-defense combat of the cooperative control and guidance; optical image encryption; fully phase encoding; joint transform correlator; fractional Fourier transform
2017-03-20;
2017-05-23。
国家自然科学基金(61377009);国家重大科学仪器设备开发专项(2013YQ290489, 2011YQ040136);国家奖学金(201506685053);黑龙江省自然科学基金(F201411);哈尔滨自然科学基金(2014RFQXJ030)。
宋 洁(1988-),女,黑龙江哈尔滨人,主要从事舰空导弹武器系统和图像加密方面的研究。
1671-4598(2017)11-0087-04
10.16526/j.cnki.11-4762/tp.2017.11.023
TP3
A

