小区开放对道路通行的影响
(天津理工大学中环信息学院 天津 300000)
小区开放对道路通行的影响
王博宇苏晓飞王启铭
(天津理工大学中环信息学院天津300000)
2016年2月21日,国务院发布《关于进一步加强城市规划建设管理工作的若干意见》,其中第十六条关于推广街区制,原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院要逐步开放等意见,引起了广泛的关注和讨论。
除了开放小区可能引发的安保等问题外,议论的焦点之一是:开放小区能否达到优化路网结构,提高道路通行能力,改善交通状况的目的,以及改善效果如何。一种观点认为封闭式小区破坏了城市路网结构,堵塞了城市“毛细血管”,容易造成交通阻塞。小区开放后,路网密度提高,道路面积增加,通行能力自然会有提升。也有人认为这与小区面积、位置、外部及内部道路状况等诸多因素有关,不能一概而论。还有人认为小区开放后,虽然可通行道路增多了,相应地,小区周边主路上进出小区的交叉路口的车辆也会增多,也可能会影响主路的通行速度。
问题
1.请选取合适的评价指标体系,用以评价小区开放对周边道路通行的影响。
2.请建立关于车辆通行的数学模型,用以研究小区开放对周边道路通行的影响。
3.小区开放产生的效果,可能会与小区结构及周边道路结构、车流量有关。请选取或构建不同类型的小区,应用建立的模型,定量比较各类型小区开放前后对道路通行的影响。
4.根据研究结果,从交通通行的角度,向城市规划和交通管理部门提出关于小区开放的合理化建议。
针对问题1,我们建立了一套完整的评价指标体系去对在不同开放条件下的道路通行能力进行逐一分析,并搜集了不同地区和同一地区不同时间的小区的相关数据,经过主成分分析得出小区周边道路的同行能力、小区所在位置等因素是影响开放与否的重要指标。
针对问题2,收集了在该领域其他学者的研究成果,针对其要求,运用层次分析法设计了一套完整的数学模型,通过对比开放前后的车流量等因素,进而解决车辆通行能力问题。
针对问题3,我们给出了新的方案,并采用新的方法讨论了其合理性,得到了较为符合实际的结论。
针对问题4,我们在前三问解决的基础上,提出了较为稳妥的建议以供参考。
评价指标体系;道路通行能力;层次分析法
一、问题重述
(一)背景
2016年2月21日,国务院发布《关于进一步加强城市规划建设管理工作的若干意见》,其中第十六条关于推广街区制,原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院要逐步开放等意见,引起了广泛的关注和讨论。
除了开放小区可能引发的安保等问题外,议论的焦点之一是:开放小区能否达到优化路网结构,提高道路通行能力,改善交通状况的目的,以及改善效果如何。一种观点认为封闭式小区破坏了城市路网结构,堵塞了城市“毛细血管”,容易造成交通阻塞。小区开放后,路网密度提高,道路面积增加,通行能力自然会有提升。也有人认为这与小区面积、位置、外部及内部道路状况等诸多因素有关,不能一概而论。还有人认为小区开放后,虽然可通行道路增多了,相应地,小区周边主路上进出小区的交叉路口的车辆也会增多,也可能会影响主路的通行速度。
(二)问题
1.请选取合适的评价指标体系,用以评价小区开放对周边道路通行的影响。
2.请建立关于车辆通行的数学模型,用以研究小区开放对周边道路通行的影响。
3.小区开放产生的效果,可能会与小区结构及周边道路结构、车流量有关。请选取或构建不同类型的小区,应用建立的模型,定量比较各类型小区开放前后对道路通行的影响。
4.根据研究结果,从交通通行的角度,向城市规划和交通管理部门提出关于小区开放的合理化建议。
二、问题分析
小区开放对周边道路的影响程度受很多因素影响,例如小区的所在位置,道路的通行能力,道路的行驶时间,延误时间等。因此研究某一地区小区开放对周边道路的影响问题需要综合考虑诸多因素,为了能更好的研究各因素的重要程度,就需要提炼出一个综合指标,并且其能够综合的反应小区开放前后对道路通行能力的影响程度。
三、模型假设
1、假定原有路程行驶时间和原有道路宽度等刚性指标相对不变。
2、假定原有小区内部的通行能力在一定时间内,不发生改变。
3、假定市区的交通都正常运行,没有突发事件影响整体城市交通的运行。
四、问题1
请选取合适的评价指标体系,用以评价小区开放对周边道路通行的影响。
查阅相关资料,某市10条城市主要道路在固定时间内的车流量相关数据如下:
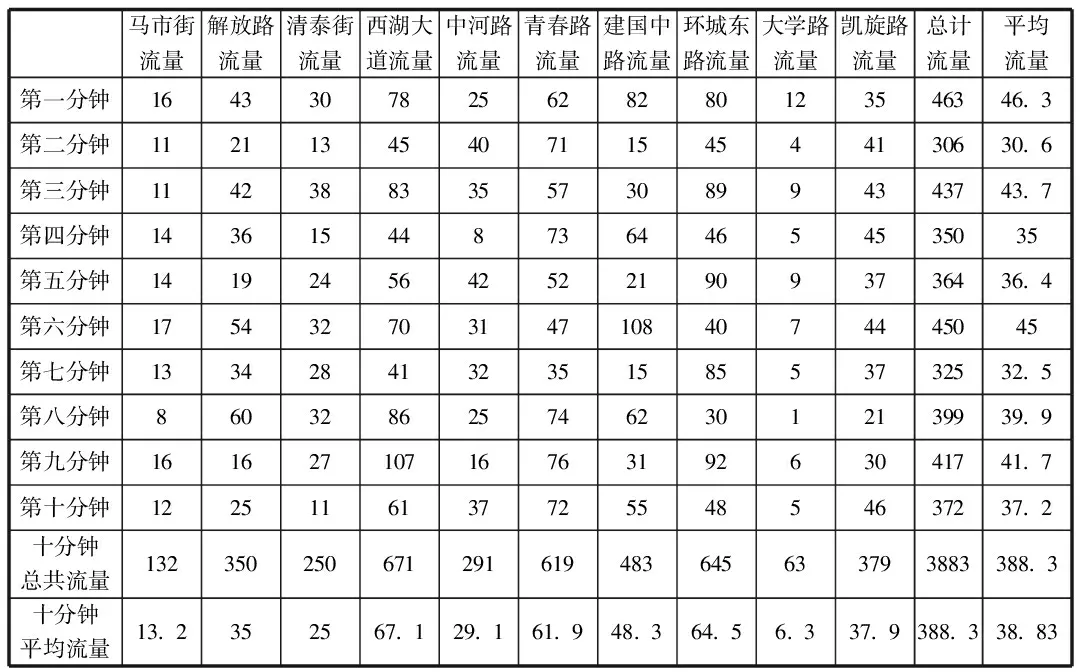
某市道路交通车流量统计表
(一)模型的建立
在用统计分析方法研究多变量的课题时,变量个数太多就会增加课题的复杂性。人们自然希望变量个数较少而得到的信息较多。在很多情形,变量之间是有一定的相关关系的,当两个变量之间有一定相关关系时,可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量,将重复的变量删去多余,建立尽可能少的新变量,使得这些新变量是两两不相关的,而且这些新变量在反映课题的信息方面尽可能保持原有的信息。
通过对数据的分析可知,影响“小区开放前后道路通行能力”的因素有很多,我们希望找出影响平衡的一个综合指标。如果考察加权平均,则主观性太大。而利用主成分分析法,可以根据每个指标的重要程度给出一个综合指标,进而全面的研究开放前后的通行能力。一般地,我们把信息完全明确的系统称为白色系统,信息完全不明确的系统称为黑色系统,信息部分明确、部分不明确的系统称为灰色系统。当事物之间、因素之间、相互关系比较复杂,特别是表面现象,变化的随机性更容易混肴人们的直觉,掩盖事物的本质,使人们在认识、分析、预测、决策时,得不到全面的、足够的信息,不容易形成明确的概念。这些都是灰色因素,灰色的关联性在起作用.
假设X0=(x10,x20,…,xn0)T为母序列,X1=(x11,x21,…,xn1)T,…,Xm=
(x1m,x2m,…,xnm)T为子序列(比较序列),则定义Xi与X0在第k点的关



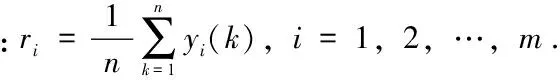
灰色关联度分析应用非常广泛.例如当需要对n个方案进行评价时,有m个指标可以从不同的侧面反映出被评价的n个方案效益的情况.于是,可采取如下步骤:
1.选定母指标:可选取对方案效益影响最重要的指标作为母指标,如选Xj为母指标.
2.对原始数据(指标值)进行处理:由于各指标的量纲不同,指标值的数量级也差别很大,为了用这些数据进行综合评价.首先必须对原始数据进行无量纲、无数量级的处理.处理的方法通常有两种:其一是均值化处理,即分别求出各个指标的原始数据的平均值,再用均值去除对应指标的每个数据,便得到新的数据;其二是初值化处理,即分别用原始数据每个指标的第一个数据去除对应指标的每一个数据,得到新的数据.

小区车辆保有数2997899122567185874332527内部通行能力182754811211107837731471所在位置5774173248674404220209094安全290672661889168659002478其他61817316595383817258796路段通行能力54011998561524267238931218交叉口通行能力2569822020631927867047682总能力266274482016.159846252357高峰期1402364510242771522367155


7.排序:将各方案的指标值带入得到该方案效益综合得分Zk,k=1,2,…,n.依据综合得分从大到小排序,也就得到个方案的综合效益的排序.
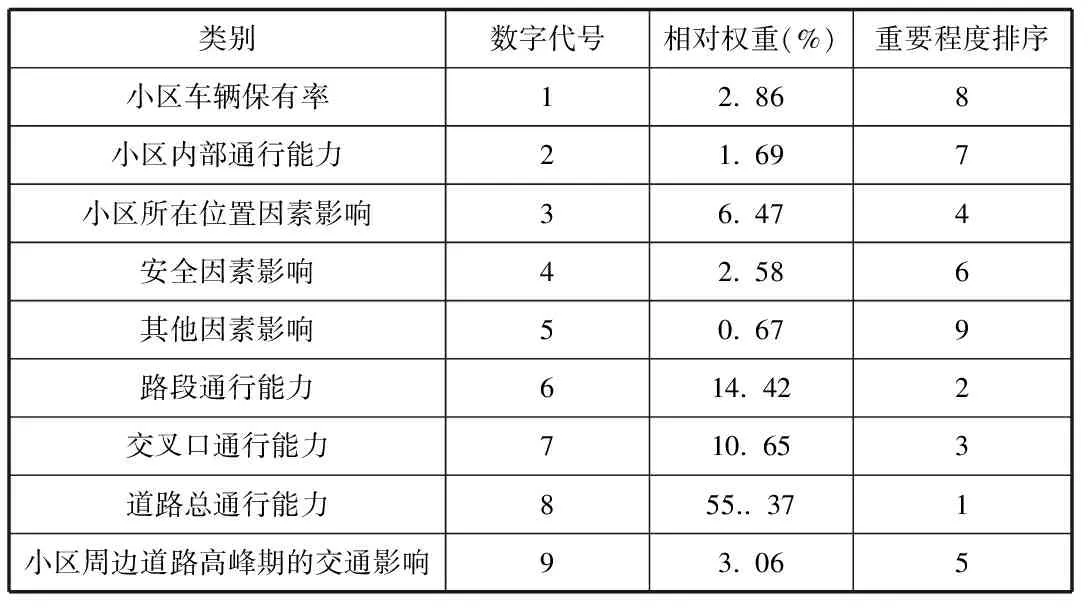
类别数字代号相对权重(%)重要程度排序小区车辆保有率12.868小区内部通行能力21.697小区所在位置因素影响36.474安全因素影响42.586其他因素影响50.679路段通行能力614.422交叉口通行能力710.653道路总通行能力855..371小区周边道路高峰期的交通影响93.065
(二)模型的求解
选取道路通行能力、道路总行驶时间、小区所在位置、路段行驶时间、交叉口延误时间(分)、安全系数等指标作为“小区开放与否对周围道路通行能力程度”的影响指标。得到如下图所示的关联法:

(三)结果分析
由最终数据可知,在众多影响因素中,起决定性作用的是道路通行能力与行程时间,其中道路通行能力有众多刚性指标约束,而行程时间则由车辆通行的实际情况决定,因此,为了定量的分析车辆通行能力,我们建立了一套新的数学模型用以分析小区开放对车辆通行的实际影响。
五、问题2
请建立关于车辆通行的数学模型,用以研究小区开放对周边道路通行的影响。
搜集该领域其他学者的研究成果可以发现,道路交通的通行能力指标与道路的类型,道路的截面宽度,车辆的速度,车辆的类型,路段行驶时间,交叉口行驶时间,总行驶时间,车流量等众多因素有关,我们根据已有的研究成果,建立了新的数学模型,用以定量的研究车辆通行能力。
1、路段行驶时间;路段行驶时间定义为将一段有路段有交叉口的实际道路抽象为一段完整的,无交叉口的模型路段,从而简化数学运算过程。
路段行驶时间是在不考虑交叉口通行能力的影响下的路段行驶能力,其计算方法如下:
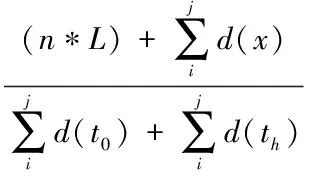
其中,不受到路交叉口的通行能力影响的计算公式如下:
νe=Nm*ac
这其中ac表示机动车道通行能力分类系数,如下表所示

计算行车速度(KM/H)50403020可能通行能力(PCU/H)1690164015501380

道路分类快速路主干路次干路支路ac0.750.800.850.90
根据上述计算方法,我们使用MATLAB进行了模型计算,得到了如下所示的结果:
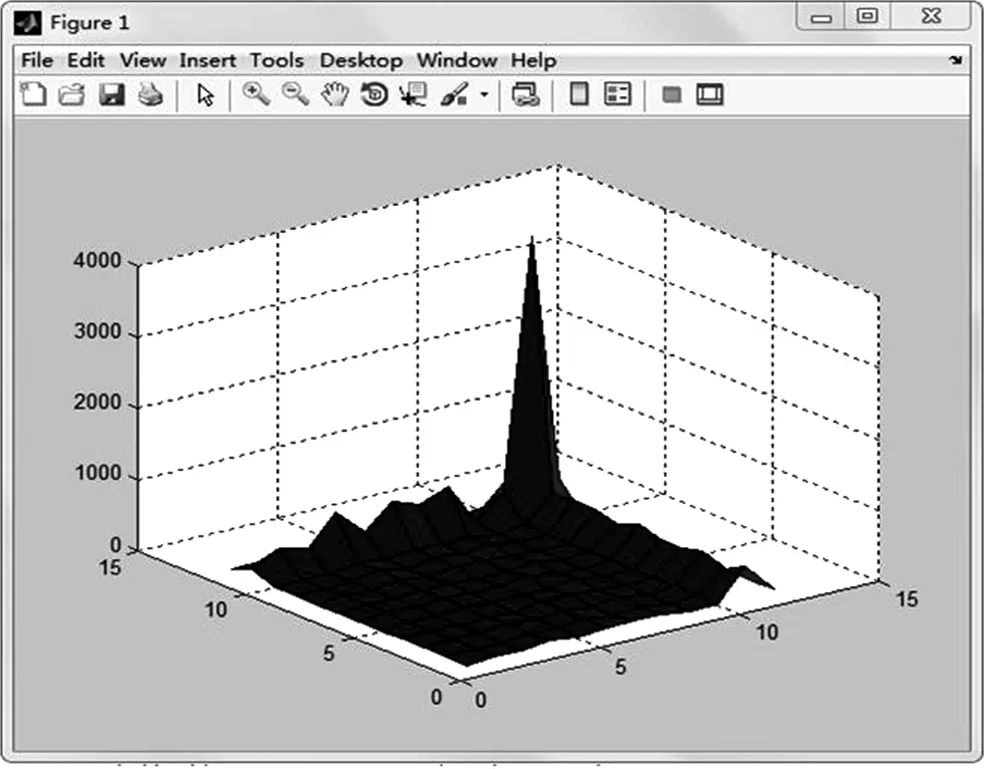
可以看到,在理想状态下,路段的通行能力基本保持不变,大多数时间均保持一定的通行能力不变。
2、交叉口延误时间:交叉口延误时间定义为在等延误原则条件下,(即各个车道延误时间均相等);可用某一车道的延误时间代替交叉口延误时间。
其中,对于一般的城市道路,在路段中车辆不仅受到行人和非机动车的干扰,而且还会受到对向车辆行驶的影响。因此,必须研究这些因素对机动车道的综合影响程度,即路旁干扰系数。毫无疑问,由于路旁非机动车及行人等的突然出现,正在机动车道上的驾驶员会意识到必须采取防范措施,以免发生意外事故,从而导致车速下降。可以认为,路旁干扰越大,车速下降越大,使道路通行能力越小。因此,我们用车速下降率作为路旁干扰系数,即路旁干扰系数。其中为受干扰后的车速为未受干扰的车速。为了研究方便,我们把受干扰道路的情况划分成以下七类:
(1)不受非机动车干扰,不受对向车流干扰,不受行人干扰的车道即四块板道路及有行人隔离的两块板机动车专用道
(2)不受非机动车干扰,不受对向车流干扰,受行人干扰的车道即无行人隔离的两块板机动车专用道
(3)受非机动车干扰,不受对向车流干扰,不受行人干扰的车道即两块板有行人隔离的机非混行车道
(4)不受非机动车干扰,受对向车流干扰,不受行人干扰的车道即一块板有行人隔离的机动车专用道及三块板道路
(5)不受非扣动车干扰,受对向车流干扰,受行人干扰的车道即一块板机动车专用道
(6)受非机动车干扰,不受对向车流干扰,受行人干扰的车道即两块板机非混行道路
(7)受非机动车干扰,受对向车流干扰,受行人干扰的车道即一块板机非混行道路。
在一系列观测基础上,分析各个道路的车速下降情况,得出干扰系数为:
第一种:a1=1;
第二种:a2=1-0.00054p
第三种:a3=1-0.00201x
第四种:a4=1-0.0027q
第五种:a5=(1-0.00054p)*(1-0.0027q)
第六种:a6=(1-0.00201x)*(1-0.00054p)
第七种:a7=(1-0.00201x)*(1-0.00054p)*(1-0.0027q)
式中:p为行人流量/5MIN
q为对向机动车流量/5MIN
x为非机动车流量/5MIN
通常情况下,路宽及侧向净空修正有国际标准做参考如下表所示:
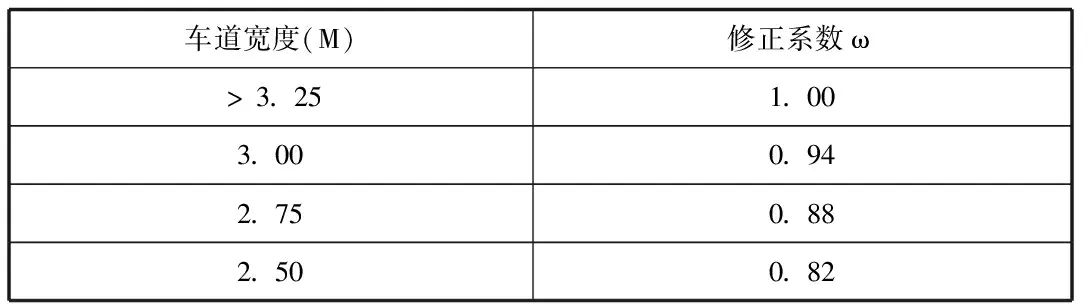
车道宽度(M)修正系数ωgt;3.251.003.000.942.750.882.500.82
侧向净空修正系数如下表所示:
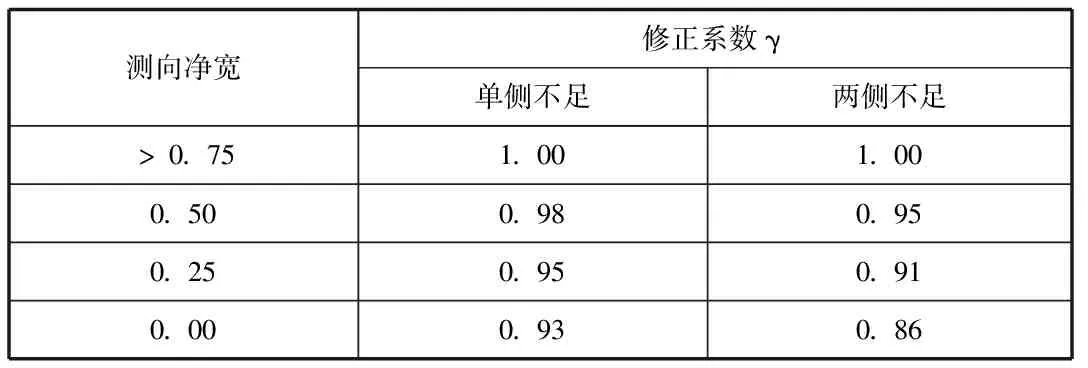
测向净宽修正系数γ单侧不足两侧不足gt;0.751.001.000.500.980.950.250.950.910.000.930.86
在实际道路设计中,为使道路在后期使用中有良好的改造能力,在规划之初即设计了“规划通行能力”如下所示:Cd=C*(V/C)*α*ω*γ
其中C表示理论通行能力
(V/C)表示某一服务水平下的饱和度
α路旁干扰修正系数
ω路宽修正系数
γ侧向净宽修正系数
其中服务水平饱和度参考如下:
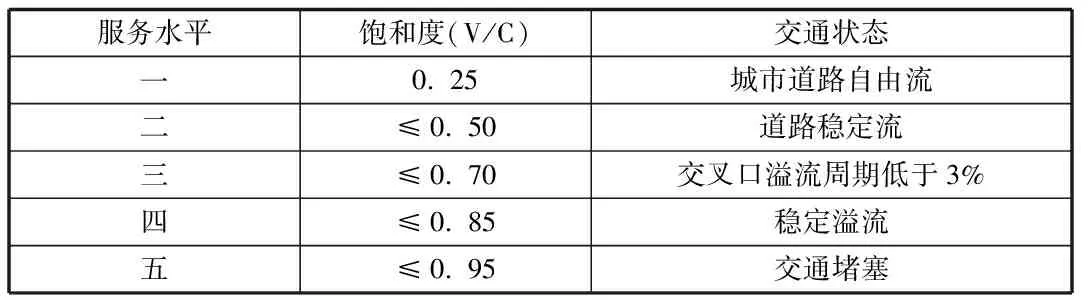
服务水平饱和度(V/C)交通状态一0.25城市道路自由流二≤0.50道路稳定流三≤0.70交叉口溢流周期低于3%四≤0.85稳定溢流五≤0.95交通堵塞
由上述分析可以看到,交叉口通行能力的影响因素有很多,合理的研究方法很重要,结合众多学者的研究成果,我们选择了美国HCM2000评价体系作为分析的依据,如下所示:

分类因素道路车道数交叉口间距车流量密度交通转向密度信号信号控制
最终选用了美国HCM2000中的延误计算公式:
d=d1(PF)+d2+d3
其中
d1为均匀到达车均延误
PF为均匀到达修正系数
d2无初始排队情况考虑车辆到达随机性的附加延误
d3为初始排队延误。
由此我们使用MATLAB进行数据处理和计算得到如下结果:
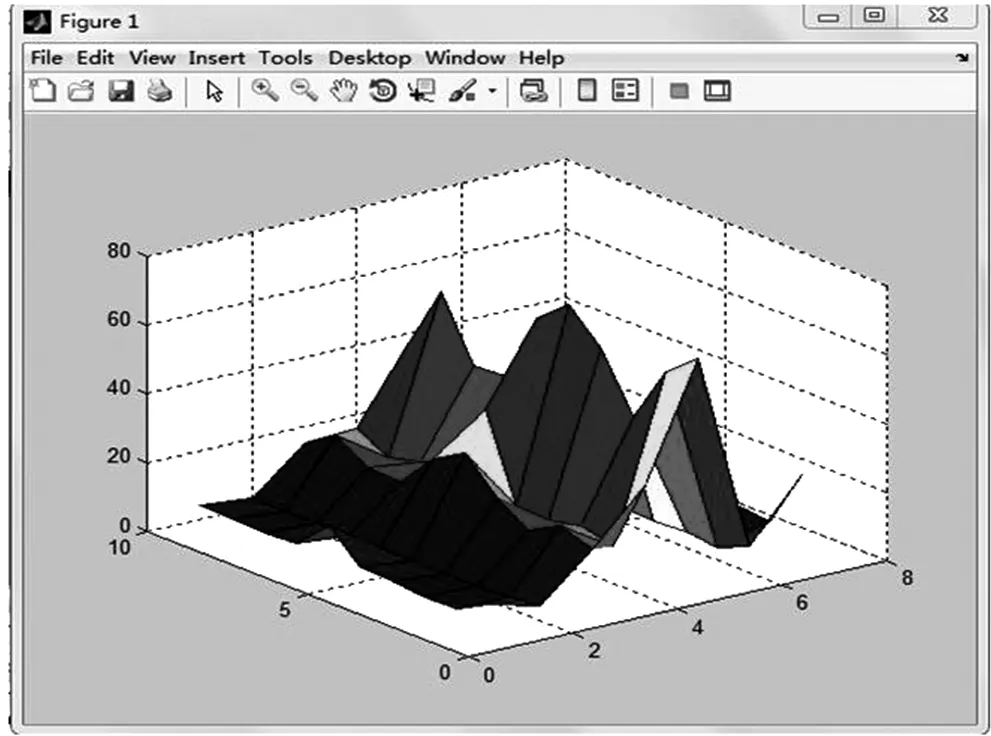
可以看到,在X轴的中间点,即时间段在中午12:00到下午3:00之间,交叉口的延误时间达到最大,其次是上午6:00到9:00之间,有一第二高峰,其余时间段延误时间均不高。
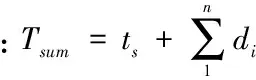
即:

由此模型我们得到了如下图所示的分析结果,该分析结果是针对小区未开放时的车辆通行能力研究,图中:
粉线代表通行能力;
亮绿线代表车流量;
蓝线代表延误时间;
红线代表总行程时间;
深绿线代表交叉口时间;

可以看到,未开放时小区各项指标均改变不大,外部交通对小区的影响有限。与此同时,我们继续研究了小区开放后的车辆通行能力,并得出了如下结论:

可以看到,开放后,小区的道路通行能力均发生了较大改变,其中,在下午4:00到6:00期间的车流量有较大增加,延误时间有所增加,通行能力下降。
六、问题三:小区开放产生的效果,可能会与小区结构及周边道路结构、车流量有关。请选取或构建不同类型的小区,应用建立的模型,定量比较各类型小区开放前后对道路通行的影响。
问题3中针对不同类型的小区开放后进行分析,我们应用上述结论,建立了如下模型
先做如下假设:(1)假设小区的人数保持稳定;
(2)车辆保有率在短时间内不会发生重大变化;
(3)假设交通秩序正常,没有影响出行的突发事件。
我们将层次分析法应用到本问题中,首先介绍层次分析法的基本理论。
1、模型的建立
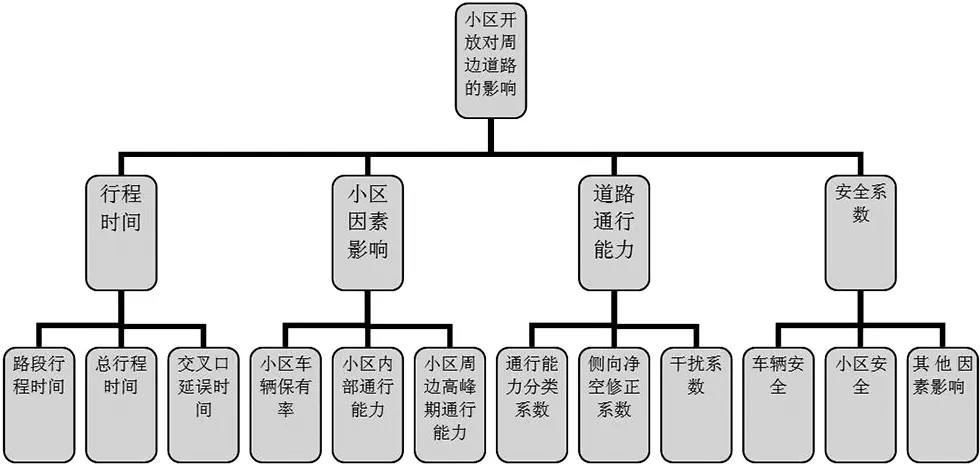
层次分析法是决策者通过将复杂问题分解为若干层次和若干因素(如图3-1),在各因素之间进行简单的比较和计算,就可以得出不同方案的权重,为最佳方案的选择提供依据。
首先,要对不同的准则做好分层:
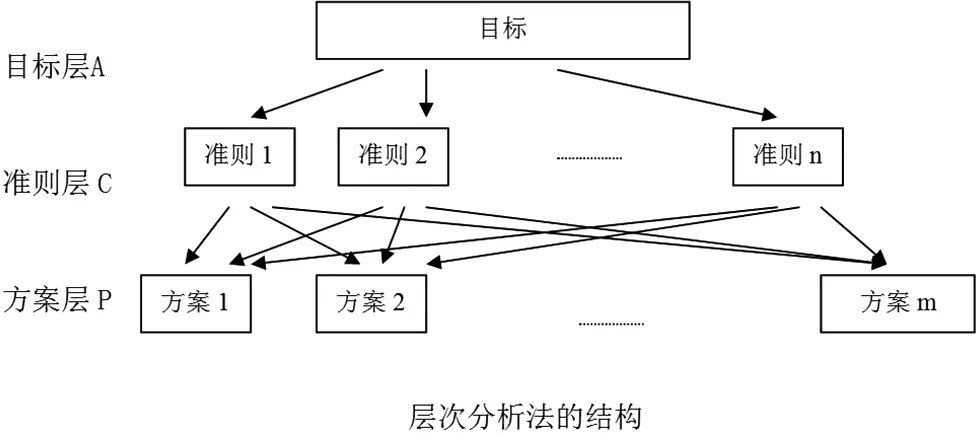
2、模型的求解

不同层的因素间都有影响,不同类的因素间也有影响,起相互影响的各个主要因素的分析结果如下
(1)小区的位置影响
图中:蓝线表示市中心开放前车流量;
绿线表示市区开放后车流量;
红线表示郊区开放后车流量;

该图表示市中心,市区,郊区开放后的车流量变化,可以看到,对于市中心与市区的小区来说,开放后,特别是在午间高峰时期,车流量居高不下。
而在郊区,车流量变化较为平稳,值得注意的是,郊区的车流量在晚间4:00到6:00之间达到最大。
此外,其他因素的影响也不能忽略,我们针对上述不同类型,定量的分析了其他因素的影响
(2)小区上下班高峰期对通行的影响

可以看出,伴随着12:00高峰期的到来,车流量也有较大增加。
(3)小区内部道路建设的影响
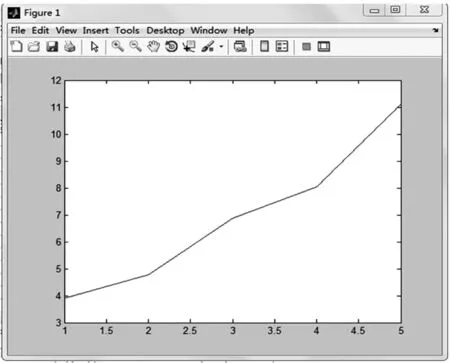
可以看出,随着小区内部道路的优化,通行能力也在增强。
(4)小区私家车保有量的影响
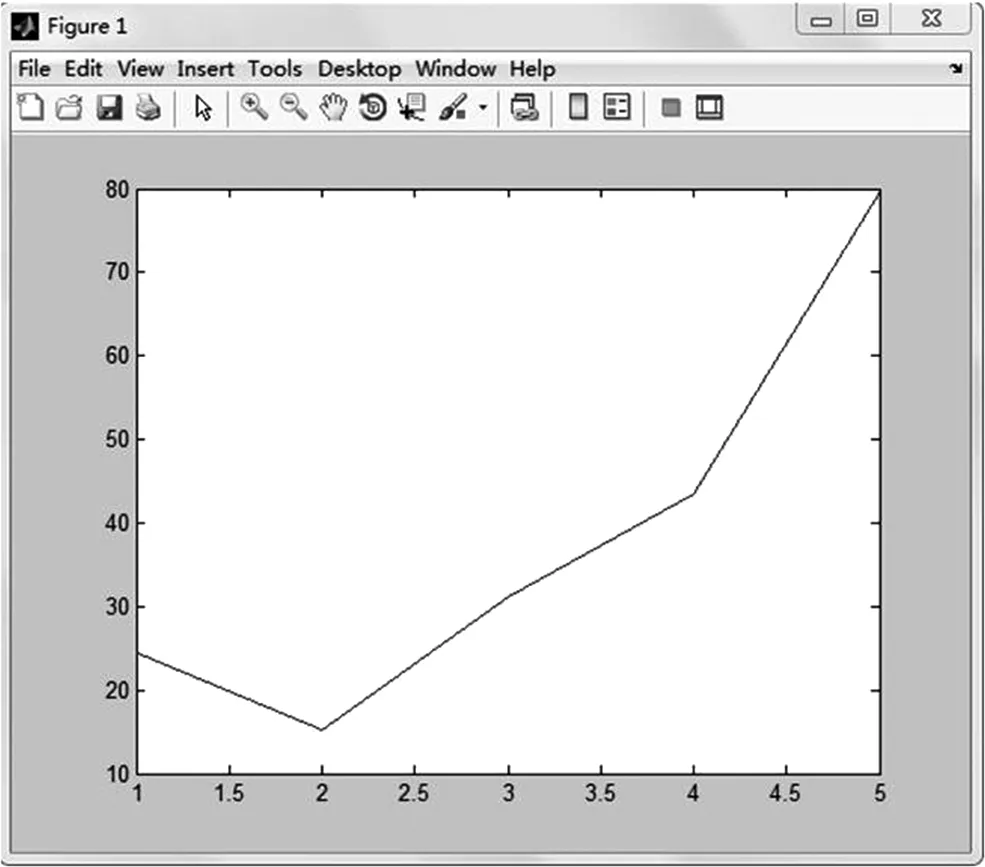
可以看出,随着小区业主私家车保有量的增加,开放后车流量增加的更快,更多。
模型的分析
综合上述结果,我们得到了最终分析模型如下所示:

图中,Z轴代表车流量密度,Y轴代表距市中心的距离(以Y轴中点为市中心),X轴代表时间,可以发现,时间在下午3:00到6:00,距市中心1到2公里处,车流量达到最大。
综上所述,我们可以得到以下结论:
(1)在众多影响小区开放后道路通行能力的因素中,影响最大的是小区自身所处的位置,这是因为,由于道路本身的通行能力一定,因而开放后小区内部的道路所能承载的通行能力也是一定的,因此在其他因素不改变的情况下,开放可以视为只是单纯的增加了道路以及交叉口的数目,而又由第二问可以看出,位于市中心和市区的道路在路段与交叉口的数目增多后,反而会更加拥堵。因此,小区自身所在位置便成为决定性的因素。
(2)第二大影响因素则是时间,由上述计算结果可以看出,无论是在市中心还是市区,无论道路通行能力有多大提升,如果不能错开行车高峰时段,只是单纯的开放小区路段,无法从根本上解决道路拥堵问题。
(3)分析小区开放对城市道路交通的利弊,必须具体情况具体分析,综合各类影响因素得出最优方案,不能以偏概全,照搬照抄,同时充分尊重小区业主的意见。
问题四:根据研究结果,从交通通行的角度,向城市规划和交通管理部门提出关于小区开放的合理化建议。
建议1:
小区开放与否与城市发展,小区内部道路密集程度,小区人口的居住数量,小区所在的地段以及小区所在路段的高峰期时间段等众多因素有关。应以:
小区所在地段gt;高峰期时间段gt;小区内部道路通行能力gt;私家车保有量为准则进行优先考虑。
建议2:
若该小区由于某种特殊原因,例如临近学校,火车站等,可依据情况分时间段开放。对于人口稀少,小区地段远离城市中心地带,为了减少安全隐患,建议不进行小区开放。
建议3:
充分征求业主意见,具体情况具体分析,综合各类影响因素得出最优方案,不能以偏概全,照搬照抄,同时慎重考虑安全因素的影响。
指导教师:李旭东
[1]李扬.基于可持续发展理论的我国公路交通发展模式研究[D].大连海事大学,2013.5
[2]茹红雷.城市道路通行能力的影响因素研究[D].同济大学,2008.3
[3]詹斌,蔡芮东,胡远程,曹梦鑫.基于城市道路网络脆弱性的小区开放策略研[J].武汉理工大学交通学院,2016.4
[4]商仲华.居住小区开发交通影响分析研究[D].长安大学,2006.6
[5]吕斌.城市居住区“开放性”模式研究[D].大连理工大学,2006.6
[6]邝先验.城市混合交通流微观仿真建模研究[D].华南理工大学,2014.9

