基于模拟退火的三维集成电路水冷散热网络优化算法
胡 风,朱恒亮,曾 璇
(复旦大学 专用集成电路与系统国家重点实验室,上海 201203)
基于模拟退火的三维集成电路水冷散热网络优化算法
胡 风,朱恒亮,曾 璇
(复旦大学 专用集成电路与系统国家重点实验室,上海 201203)
三维集成电路(3D-IC)通过在垂直方向堆叠多层芯片有效提高了芯片的性能和集成度.然而,过高的功率密度和温度成为3D-IC集成度提高的最大障碍.水冷散热技术将冷却液注入两层芯片间的沟道有效解决了3D-IC的散热问题,同时也带来了过高温度梯度的问题以及对散热功耗,芯片可靠性的要求.本文提出一种在有硅穿孔限制下的基于模拟退火的沟道网络优化算法,算法基于温度仿真,对散热沟道进行放置与填充操作,设计出的沟道网络可以有效降低散热功率和温度梯度.实验中,与传统的均匀直沟道的设计方法相比,我们的方法可以在相同最高温和温度梯度限制条件下,降低散热功率达67.0%.
三维芯片; 水冷散热; 沟道网络优化; 模拟退火

图1 三维集成电路水冷散热系统示意图[1]Fig.1 Demonstration of liquid cooling system in 3D-IC[1]
近几年来,三维堆栈芯片制造技术获得了长足的发展.三维集成电路(3D-IC)将多层芯片垂直堆叠在一起,层与层之间通过硅穿孔(Through Silicon Vias, TSV)相连,有效减少了互连线规模,提高了芯片性能和集成度.严重的散热问题(功率密度高达250W/cm2)阻碍了三维集成电路向更高集成度的方向发展.风冷散热被证实无法有效带走芯片内部热量,水冷散热成为三维集成电路散热问题最有希望的解决方法[1].通过在硅片背部刻蚀出沟道并将两层硅片结合在一起,在微型水泵的驱动下,水或其它散热剂流过两层芯片间的沟道(Micro-channels),水流的强大散热能力可以迅速带走芯片内部产生的巨大热量(图1).Tuckerman和Pease实验证实水冷散热可带走高达800W/cm2的热流密度并使芯片工作在85℃下[2].并且相对于传统的风冷散热,水冷散热极大降低了所需的散热功率.在这些优点之外,水冷散热技术也带来了过冷却和过高的温度梯度的问题,过高的温度梯度会降低芯片的可靠性和寿命,带来芯片设计上的障碍.
对水冷散热沟道网络进行优化,首先要对三维芯片进行温度仿真.得到广泛接受的是名为3D-ICE的热分析工具所采用的瞬态紧凑热模型,水流在模型中等效为受控热流源[3].马里兰大学帕克分校的Shi将水流进一步简化为热阻[4].以上两者都只处理单沟道的情况,没有考虑沟道交叉的情形,为了计算带有复杂沟道网络的三维集成电路温度分布,我们在3D-ICE的热分析模型基础上做了进一步的拓展.
IBM的Mohamed在均匀分布直沟道情形下,提出沟道温度和沟道宽度关系的解析表达式,通过调节沟道宽度的方法降低温度梯度并节约散热功率[5];Shi提出了非均匀放置直沟道的试探性解法,以此降低散热功率和温度梯度[4].以上方法都只针对直沟道的情况.
2015年国际计算机辅助设计比赛(CAD contest at ICCAD)提出了复杂沟道网络的优化问题[6].本文针对这一问题,提出复杂沟道网络下的热分析模型和基于模拟退火方法的沟道网络的设计优化算法.算法的核心思想是初始化时放置尽可能多的沟道,然后基于模拟退火算法,对沟道网络不断进行以填充为主的操作.相比于传统均匀直沟道散热方法,基于模拟退火方法的沟道网络优化算法可极大降低散热沟道网络所需散热功率.
1 背景介绍
水冷散热沟道处在一片硅片的背部,通过将两层硅片堆叠在一起,使微型散热沟道嵌入两层硅片之间,发挥水的强大散热能力.有源层为三极管和导线所在层,也是热源所在层.为简单起见,本文对单层沟道层、双层有源层三维芯片进行研究.单沟道层三维芯片结构如图2所示.
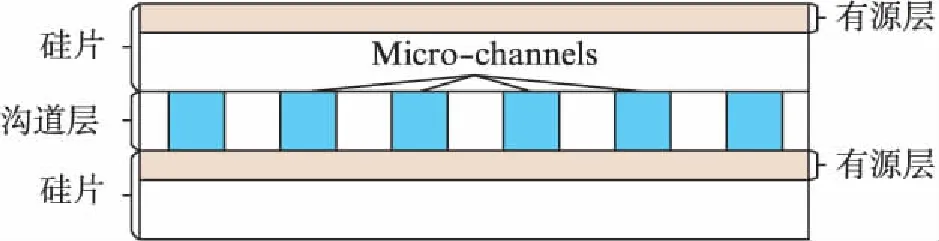
图2 双有源层三维芯片侧视结构图Fig.2 The side view and structure of 3D-IC with two source layers

图3 散热沟道网络示意图Fig.3 Liquid cooling channel network
2015年CAD contest at ICCAD给定三维芯片的几何结构、沟道层高度以及材料的各种物理特性如热传导系数、热容、热对流系数[6].水冷散热沟道网络的表示和设计遵循以下规则: 沟道层在水平面内被划分成如图3所示的n×n的边长为100μm的正方形网格,其中标注为-1的浅棕色方格代表预留放置层间TSV的区域,不可以放置沟道.标注为0的棕色格子代表可以放置沟道的区域,材料为硅.图3中,标注为1的浅蓝色方格代表沟道区域,材料为水.在边界处,标注为2的深蓝色格子代表水流流入的入口,标注为3的红色格子代表水流流出的出口.当方格太密时,以颜色表示方格类型,红色箭头指示出口区域,蓝色箭头指示入口区域.考虑到可制造性原因,入口出口必须处于连续的区域中,在4条边上,入口区域和出口区域最多交替一次.在入口出口处会有微型水泵为散热系统提供冷却剂的循环,所有入口出口施加相同压强差P.在这些约束条件下,完成对散热沟道网络的设计和入口出口压强差P的选取.
水冷散热沟道网络的设计目标为在最高温、最大温度梯度、入口出口、TSV等约束条件下,通过设计沟道网络和选取入口出口压强差P,最小化水泵所需要提供的散热功率,优化问题可描述为
minEpump
s.t. max(T)≤Tmax
(1)
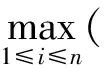
其中:Epump是水泵提供的散热功率,优化目标为最小化Epump,s.t.之后内容为优化约束条件;T为所有芯片有源层温度分布向量;Tmax为最高温限制条件;Tmax为温度梯度限制条件;max(T)为所有有源层的最高温,应不大于Tmax;Ti为第i层有源层温度分布向量;n为有源层数量;Ti为第i层有源层温度梯度,定义为本层最高温和最低温之差,即
Ti=max(Ti)-min(Ti),
(2)
(3)
其中:Vn为流过第n个入口的体流量;Nc为入口个数.
2 水冷散热网络热分析模型
由于3D-ICE中的热分析模型只能分析直沟道的情形,沟道不交叉.我们在3D-ICE的稳态紧凑热模型的基础上进行扩展,开发出可进行沟道网络温度仿真的热分析模型.在固体材料上,我们采用和3D-ICE相同的模型.模型采用传统的电路类比方法,温度对应电压,热流对应电流,热阻对应电阻,热容对应电容,最终可将热分析问题转化为电路问题进行仿真[7],固体材料中的热分析模型可参考文献[3].
散热沟道网络优化针对稳态情况,在稳态条件下,温度分布不随时间变化,在流动液体中的热守恒方程如下:
·(-k
(4)
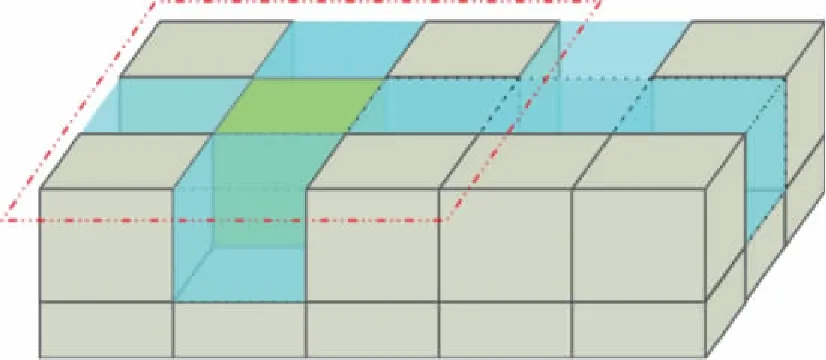
图4 网格划分后的交叉液态沟道网络Fig.4 Discretized crossing liquid channel network
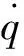
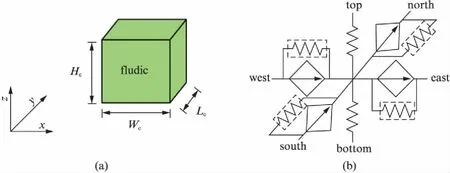
图5 交叉沟道网络中心离散方格及其等效热分析模型Fig.5 The center liquid cell in crossing channel network and its equivalent thermal analysis model
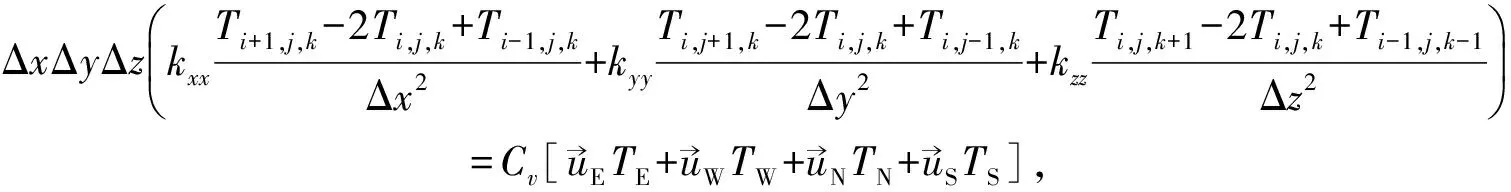
(5)
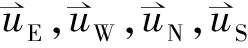
(6)
将式(6)代入式(5)中可得:
(7)
从式(7)等效出的热分析模型如图5(b)所示,式左端等效为图5(b)中6个方向上的等效热阻,若相邻方格为固态方格,则此方向上等效热阻由热对流引入,若相邻方格同为液态方格,则此方向等效热阻由热传导引入.式右端4项可等效为4个水平平面内可类比于受控电流源的受控热流源.
接下来将热分析模型运用到三维芯片的所有离散方格中,组成整体等效电路.在沟道层的入口方格处,按照狄利克雷(Dirichlet)边界条件,设定方格入口边界面的温度为恒定值,即流入冷却液的温度恒定.在沟道层的出口方格处,按照纽曼(Neumann)边界条件设定方格出口边界面温度与方格中心温度相同.通过与分析电路相同的方法构建矩阵求解,即可得到芯片的温度分布.
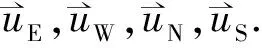
(8)
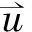
3 基于模拟退火方法的沟道网络优化方法
散热沟道网络优化的目的是在最高温和温度梯度等约束条件下,尽可能降低所需散热功率.一方面,在沟道中,过量的水流流过功率密度较低区域的上方或下方会导致散热功率的浪费,引起温度梯度的上升.因此填充低温区域可以有效降低温度梯度,节约散热功率.另一方面,无法保证填充的每一步都有利于获得全局最优解的沟道网络,需要对一些被填充区域重新放置沟道进行校验.我们算法的核心思想是先在所有可放置沟道处放置沟道,然后通过仿真比较,在模拟退火算法框架下,迭代进行沟道的填充与重新放置操作.最终调整入口出口压强差,得到最终结果.
3.1 沟道网络的入口出口
首先,我们要为散热沟道网络安排入口出口.入口出口可分为如图6所示3类.传统的散热沟道方式为如图6(a)所示的均匀直沟道,水流从芯片的一条边注入,从相对的边流出.图6(b)所示的沟道网络和传统方式相比,入口出口平均距离缩短,更短的沟道长度意味着热量可以更快地被带出,有利于降低压强,节约散热功率.更进一步,如图6(c)所示,可以将沟道层划分成隔离的4个区域,每个区域的入口出口位置可交换,可生成16种入口出口的排布.对这16种入口出口排布的初始沟道网络进行温度仿真,可选出最适合当前有源层功率分布的入口出口排布,本文以此方法确定沟道网络的入口出口排布.

图6 (a) 均匀分布直沟道,(b) 初始沟道网络,(c) 划分成隔离的4个区域的初始沟道网络Fig.6 (a) Uniformly distributed straight channels, (b) initial channel network, (c) initial channel network isolated into 4 regions

图7 基于模拟退火的沟道网络优化流程图Fig.7 Flow chart of simulated annealing based channel network optimization
3.2 基于模拟退火的沟道网络优化流程
水冷散热网络的优化算法基于模拟退火框架[9],算法流程如图7所示.模拟退火算法在搜索解空间时带有随机性,并以一定概率接受比当前差的解,接受概率与退火温度tsa有关.模拟退火算法可以有效避免陷入局部最优解的陷阱.
模拟退火每次操作有2种选择: 填充一个液态沟道方格或在一个固态方格处重新放置沟道.填充液态沟道方格时,首先在上下两层有源层中选择温差最大的一层的温度分布作为沟道层的温度分布.在沟道层的液态沟道网格中,将未被选择过的沟道方格按温度从低到高排序.排序后,从中随机选取一个沟道方格进行填充,温度越低的方格被选中的概率越大,每个方格被选中概率按其排名r取r-n后做归一化处理,n是可调参数,n=0时,沟道方格选取方式退化为完全随机方法,n=+时等同于贪心方式,即每次选取温度最低的未被选取过的沟道方格,通过在正整数中合理选取n的数值可结合贪心和随机两种选取策略,获得更好的填充效果.因为模拟退火算法的特性,有些被接受的填充操作会使温度梯度上升,因此引入重新放置沟道操作以减少此类填充操作的影响.在重新放置沟道操作中,随机选取一个之前填充过后使温度梯度上升的固态方格并重新放置沟道.优化以填充操作为主,重新放置沟道为对填充操作的修正与校验,需要之前进行大量沟道填充操作,因此填充操作被选中概率更大,填充与放置沟道操作被选中概率比例选取为9∶1可兼顾优化结果与运行时间.在以上2种操作执行中,需要以填充的方式消除沟道网络中出现的流量为0的不连通的沟道以及沟道内流量很小的区域.
对沟道网络进行操作后,需在与之前沟道网络相同Epump下,对新沟道网络进行仿真.如果温度梯度下降则接受此次操作,否则按一定概率接收.某一方格被选中进行填充或放置沟道操作后则不会被再次选中进行同类操作;如果填充液态沟道方格后温度梯度上升但仍接收此操作,则记录此方格作为重新放置沟道操作的候选区域.此后,若温度梯度或最高温超过设定范围则调整Epump使最高温低于约束条件并使温度梯度处于和约束条件相差不大的范围内,因Epump与温度梯度不一定为单调关系,需采用多起始点二分查找的方法寻找使最高温和温度梯度处于限定范围内的Epump.
上述过程循环执行,到达一定操作次数后执行退火操作tsa←α·tsa,α为退火系数,决定退火操作的快慢,通用做法为在97%~99.5%范围内进行选取,α过大会增加多余的运行时间,过小会导致无法获得全局最优解,本文选取0.98左右,具体数值按照问题不同需进行调整.tsa影响对沟道网络所做操作的接受概率,当在某一tsa下操作拒绝比例已超过99%时,则模拟退火过程已达到稳态,此时退出模拟退火过程.若操作次数达到液态方格总数时也应结束此过程.
3.3 入口出口压强差的选取
沟道网络的优化过程中需要在相同散热功率下进行多次仿真,以此评估改变前和改变后的沟道网络散热性能.通过式(3),(8)可知,Epump∝P2,因此,在后一次仿真时需要调整P使Epump与前一次相同.在沟道网络优化过程结束后,需要调整P,使温度梯度约束条件或最高温约束条件恰好得到满足,以此最小化Epump,得到最终结果.
4 实验结果及分析
为了验证基于模拟退火的沟道网络优化算法的有效性,使用2015年CAD contest at ICCAD发布的5个测例[6]来进行验证,对比在相同温度梯度,最高温以及其他限制条件下,如图6(a)所示的传统均匀直沟道、如图6(c)所示的初始化沟道网络和基于模拟退火的优化算法设计出的沟道网络的散热能力.传统均匀直沟道、初始化沟道网络按照水流流入流出方向分别有4种、2种方案,我们选取散热效果最优的方案进行对比.
测试用例1,2,3,4的功率分布信息为对IBM的UltraSPAC T1(Niagara)[10]芯片实测所得,最大功率密度为53W/cm2.测例5为官方设定,最大功率密度176W/cm2.测例1~5的尺寸均为10mm×10mm,表3中列出了测例1~5的沟道高度、最高温、最大温度梯度优化约束条件,最终优化结果的散热功率,最高温,温度梯度,压强等参数以及测例在直沟道和初始沟道网络下所需散热功率.接下来选取测例1和测例3的优化结果进行详细的讨论.
4.1 测例1
测例1最高温不能超过85℃,最大温度梯度不能超过15℃,传统直沟道、初始化网络、基于模拟退火方法优化后的沟道网络所需散热功率Epump以及对应压强P如表1所示.表1中,所有结果刚好满足温度梯度约束条件且满足最高温约束条件,基于模拟退火的沟道网络优化算法优化后的沟道网络相比于初始沟道网络和传统直沟道网络,可节约散热功率达67.0%和91.2%.

表1 测例1中相同限制条件下沟道网络所需散热功率对比Tab.1 The results comparison among different cooling networks in test case 1
图8(a)为最终优化后的沟道网络,图8(b)、(c)分别为对应的上、下有源层温度分布图.结合图8(b)、(c)可以看出,基于模拟退火的沟道网络优化算法在低温的入口区域进行了有效的填充,有效减小了散热功率在低温区域的浪费.因水流从入口到出口的过程中不断吸收热量,水温上升,散热能力逐渐下降,在出口处形成了高温区域,最高为56.3℃.在靠近出口处,通过消除流量很小的沟道形成了直沟道区域,体现出靠近出口处单一的水流流向.
从结果的对比中可以看出,经优化后,水冷散热网络相对于传统均匀直沟道散热方式具有巨大的优势.相比于初始沟道网络,通过优化散热网络可以极大地降低所需散热功率.
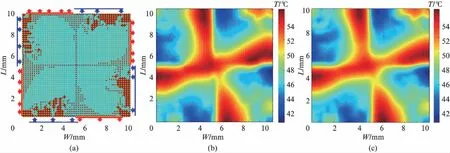
图8 (a) 测例1沟道网络优化结果,(b) 测例1上层有源层温度分布,(c) 测例1下层有源层温度分布Fig.8 (a) Optimized channel network in test case 1, (b) temperature distribution of top source layer in test case 1, (c) temperature distribution of bottom source layer in test case 1
4.2 测例3
测例3沟道高度为400μm,最高温和最大温度梯度限制条件分别为85℃、15℃,相比于测例1,额外的约束条件为沟道层中心的长方形区域不可放置沟道.优化后沟道网络以及上下2层有源层温度分布如图9(见第486页)所示.
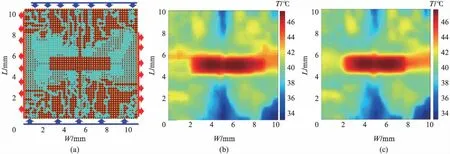
图9 (a) 测例3沟道网络优化结果,(b) 测例3上层有源层温度分布,(c) 测例3下层有源层温度分布Fig.9 (a) Optimized channel network in test case 3, (b) temperature distribution of top source layer in test case 3, and (c) temperature distribution of bottom source layer in test case 3

表2 测例3中相同限制条件下沟道网络所需散热功率对比Tab.2 The results comparison among different cooling networks in test case 3
测例3中,由于中心区域不可放置沟道网络的限制,最高温出现在了中心区域,为48.1℃.为降低中心区域温度,入口出口的选取与测例1有所不同,图9(a)中的入口出口可使中心高温的长方形区域与流入的较冷水流有充分的接触.传统直沟道、初始化网络、基于模拟退火方法优化后的沟道网络所需散热功率Epump以及对应压强P如表2所示.经优化后,所需散热功率相比与传统直沟道,初始沟道网络节省32.4%和85.6%.
4.3 综合结果
表3中为测例1~5的优化约束条件,沟道优化结果以及与均匀直沟道、初始沟道的性能对比.h为沟道层高度,Tmax为最高温约束条件,Tmax为最高温度梯度约束条件,Epump为最终优化结果所需散热功率,max(T)为优化结果的最高温,T为优化结果温度梯度,P为结果所需压强,t为优化过程所用时间,Estraight、Einitial为满足优化约束条件时均匀直沟道、初始沟道网络所需散热功率.测例1~5单次仿真平均用时1.9s.测例4有双层沟道层,规模较大,仿真次数较多,其它测例仿真次数约为1000次左右.
表3 测例1~5优化约束条件与优化结果Tab.3 The optimization constraints and results in test case 1—5
注: “—”表示不符合约束,故无结果.
在测例1~4中,最高温,最大温度梯度均符合约束条件.相比于均匀直沟道,基于模拟退火的沟道优化算法可降低散热功率达32.4%~67.0%;相比于初始沟道网络,基于模拟退火的沟道优化算法可降低散热功率达85.6%~91.9%,有效提高了水冷散热沟道网络的散热能力.在测例5中,由于过高的功率密度,温度梯度最终为10.6℃,略高于温度梯度约束10℃.经实验均匀直沟道和初始沟道网络在所有散热功率下也都不能满足温度梯度约束要求,在与优化后结果相同的散热功率下,其温度梯度分别为26.4℃,35.3℃,体现出沟道优化算法对芯片温度梯度的有效改善.
5 结 语
针对国际上最新提出的三维集成电路水冷散热网络优化问题,本文提出了一种基于模拟退火的沟道网络优化算法.算法的核心思想是基于模拟退火框架,对沟道网络进行填充和放置沟道的优化操作.经过实验验证,和传统均匀直沟道相比,基于模拟退火的沟道网络优化算法可以有效节约沟道网络所需的散热功率.
[1] BRUNSCHWILER T, SRIDHAR A, ONG C L,etal. Benchmarking study on the thermal management landscape for three-dimensional integrated circuits: from back-side to volumetric heat removal [J].JournalofElectronicPackaging, 2016,138(1): 109-117.
[2] SERAFY C, BAR-COHEN A, SRIVASTAVA A,etal. Unlocking the true potential of 3-D CPUs with microfluidic cooling [J].IEEETransactionsonVeryLargeScaleIntegration(VLSI)Systems, 2016,24(4): 1515-1523.
[3] SRIDHAR A, VINCENZI A, RUGGIERO M,etal. 3D-ICE: Fast compact transient thermal modeling for 3D ICs with inter-tier liquid cooling [C]∥Proceedings of the International Conference on Computer-Aided Design. New Jersey, USA: IEEE Press, 2010: 463-470.
[4] SHI B, SRIVASTAVA A. TSV-constrained micro-channel infrastructure design for cooling stacked 3D-ICs [C]∥Proceedings of the 2012 ACM International Symposium on Physical Design. New York, USA: ACM, 2012: 113-118.
[5] MOHAMED S, ARVINDS, MENG, J,etal. An energy-efficient liquid cooling design technique for 3-D MPSocs via channel width modulation [J].IEEETransactionsonComputer-AidedDesignofIntegratedCircuitsandSystems, 2013,32(4): 524-537.
[6] SRIDHAR A. 2015 CAD contest at ICCAD [EB/OL]. Austin, USA: CAD Contest, 2016,http:∥cad-contest-2016.el.cycu.edu.tw/CAD-contest-at-ICCAD2016/index.html.
[7] LIENHARD J H. A heat transfer textbook [M]. New York, USA: Courier Corporation,2013: 6-10.
[8] SHAH R K, LONDON A L. Laminar flow forced convection in ducts: a source book for compact heat exchanger analytical data [M]. Cambridge, Massachusetts, USA: Academic Press,2014: 196-219.
[9] HWANG C R. Simulated annealing: theory and applications [J].ActaApplicandaeMathematicae, 1988,12(1): 108-111.
[10] LEON A S, KENWAY T W, JINUK S L,etal.A power-efficient high-throughput 32-thread SPARC processor. Power Delivery [J].IEEEJournalofSolid-StateCircuits, 2007,42(1): 7-16.
SimulatedAnnealingBased3D-ICLiquidCoolingNetworkOptimizationAlgorithm
HUFeng,ZHUHengliang,ZENGXuan
(StateKeyLaboratoryofASICamp;Systems,FudanUniversity,Shanghai201203,China)
Three-dimensional integrated circuits(3D-IC) improves the performance and integration of integrated circuits effectively. But the severe thermal problem becomes the bottleneck of its development. Interlayer liquid cooling network has been proposed as an effective cooling mechanism for heat dissipation in 3D-IC. New problems such as over-cooling and high temperature gradient emerge. In this paper, a simulated-annealing based cooling network optimization algorithm is proposed under the TSV constraint. The overall cooling network optimization is an iterative process of attempting to fill and place liquid channel cells based on simulation. Numerical results show that, under the same thermal constraints, optimized liquid cooling network can save up to 67.0% cooling energy in comparison with straight micro-channel network.
3D-IC; liquid cooling; channel network optimization; simulated annealing
0427-7104(2017)04-0480-08
2016-10-04
国家自然科学基金(61376040)
胡 风(1992—),男,硕士研究生;朱恒亮,男,讲师,通信联系人,E-mail: hlzhu@fudan.edu.cn.
TN403
A

