基于滑动轴承振动模型的轴频电流建模与仿真

崔海超，嵇 斗，李 洋



基于滑动轴承振动模型的轴频电流建模与仿真

崔海超1，嵇 斗1，李 洋2

（1.海军工程大学电气工程学院，武汉 430033；2. 91315部队，辽宁大连 116041）

针对舰船轴频电场信号源的发生机理和应用研究的问题，建立了一种轴频电流的等效电路模型。模型基于滑动轴承的涡动现象，采用短轴承理论对轴承运动微分方程进行了求解，获得了轴径轨迹，然后结合电接触理论，建立了滑动轴承电接触电阻模型，对轴频电流的变化趋势进行了仿真，并将仿真结果与实船轴频电流进行了对比，结果表明，所建模型直观简便，轴频电流与实测结果的基波和二次谐波吻合较好。

滑动轴承 振动 接触电阻 轴频电流

0 引言

随着传感技术和信号处理技术的发展，作为一种重要的物理场，舰船电场受到了广泛关注[1]。舰船轴频电场是一种频率较低且特征明显的电磁场，衰减速度慢、传播距离远，可以被远程侦测，现已基本形成了完备的理论体系[2,3]。目前在水下舰船轴频电场分布特性方面，已经有了较多的建模方法和研究成果[4]，但在其产生机理方面，大多数研究均放在复杂的电化学分析方面[5]，得到的结果往往不能简便的反应舰船水下电场的特征。如果在一定条件下，把来源复杂并且影响舰船水下电场分布的主要因素理想化为简单的电路元件，建立一种直观简单便于分析的等效电路模型，对于研究舰船水下电场分布具有重要意义。公开的文献资料显示在舰船轴频电流等效电路模型的方面研究较少，文献[6]阐述了轴频电流的产生机理，建立了简单的轴频电流回路，对于回路中的等效电阻进行了粗略的估算，但缺乏对回路中等效电阻形成的机理研究，本文以滑动轴承的振动为基础，研究了滑动轴承的接触电阻变化，建立了一种简化的轴频电流等效电路模型。

1 滑动轴承振动模型

分析舰船滑动轴承的润滑油膜的工作原理可知，滑动轴承油膜力形成的收敛楔产生的支撑力的方向与滑动轴承所受载荷的方向会有一个夹角，可以将该支撑力分为两部分，一个分量是与滑动轴承所受载荷在同一条直线上但方向相反的力，一个分量是与滑动轴承所受载荷相垂直的一个力，此力是形成舰船滑动轴承周期性振动的根源[8,9]。

本文采用无限短的滑动轴承模型进行建模，假设轴径质量分布均匀，对于一个非线性转子-轴承系统，考虑其有两个自由度的稳态周期，将湍流的影响计入其中使用湍流润滑系数对雷诺方程加以改进。本模型采用直角坐标系，对舰船滑动轴承的非线性油膜力进行分析计算，此模型在直角坐标系中的力学模型如图1所示。

由图1可知此模型为一个对称性的结构，其无量纲的运动微分方程可用下式表示：

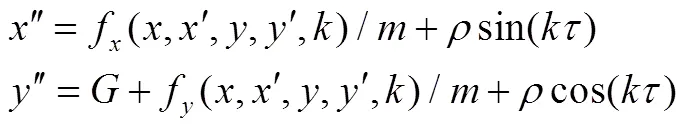
无量纲质量偏心距：

无量纲非线性油膜力分力

其中：为正整数，当=1时，方程有同步或超谐解，当>1时，方程有亚谐解；为轴承偏心距（m）；为轴承半径间隙（m）；无量纲化油膜力因子（N）：

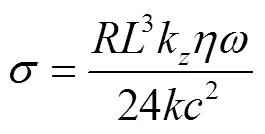
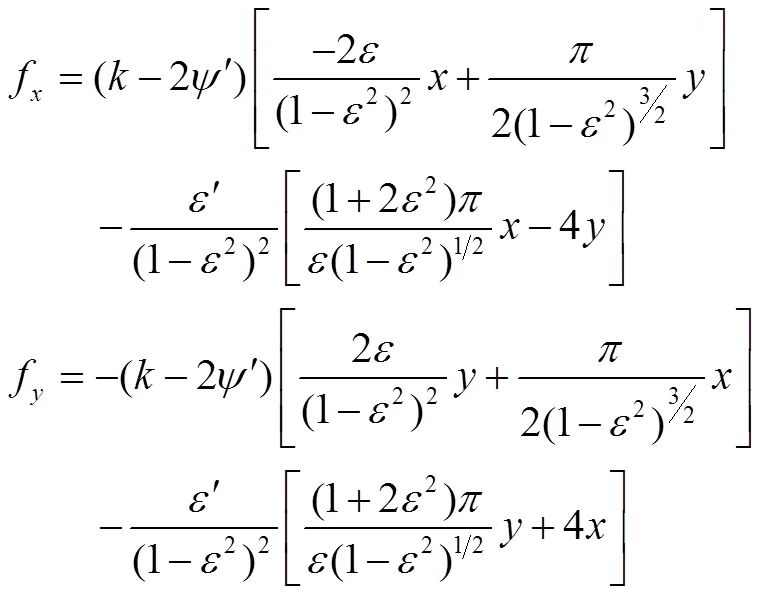
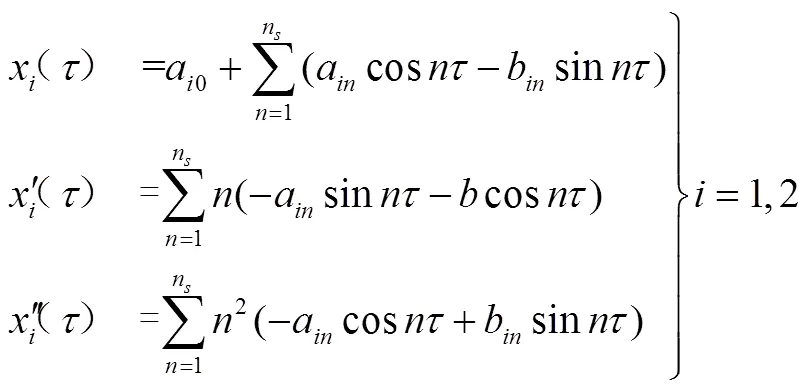
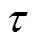
=334.0（rad/s）,=0.015(mm),=1。在计算结果中大于两阶的谐波项系数已收敛为高阶小量，由前两阶谐波构成的同步周期解为：

其轴心轨迹如图2所示：

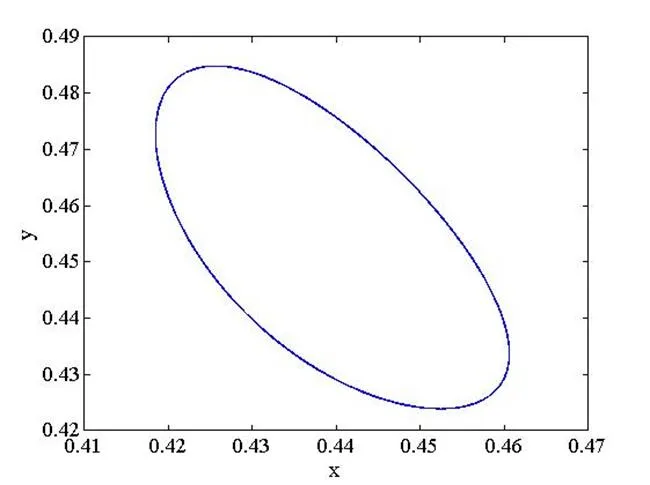
图2 滑动轴承轴心轨迹

将（4）式代入（2）式可得无量纲油膜力分量x和分量f，则无量纲油膜力:

图3非线性油膜力随时间的变化关系

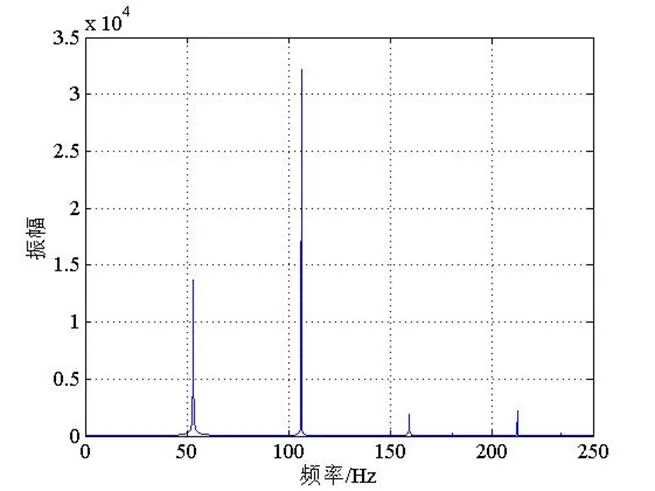
图4非线性油膜力的幅频特性

舰船推进轴系轴径旋转速度相对较小，一般会产生同步振动并伴随有相应的倍频出现[12]，故对无量纲微分方程k>1时的亚谐解不进行过多研究。从图2可以看出舰船滑动轴承轴径在发生同步振动时，滑动轴承轴径的轴心轨迹为一个椭圆。

2 轴频电流的推导与建模

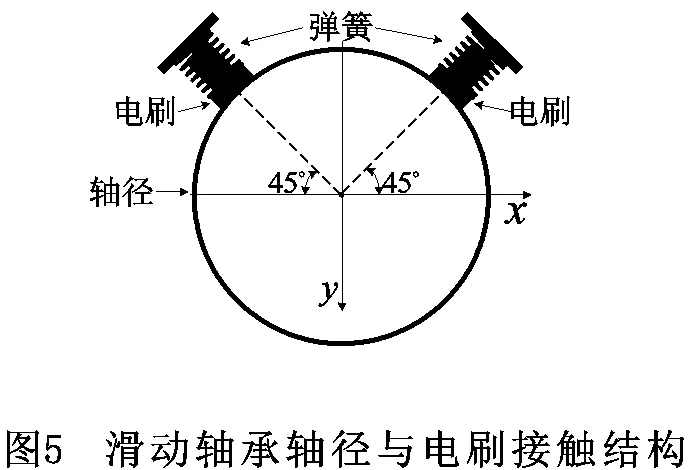
通过对舰船船体进行电场实验过程中发现，舰船的轴系部件中轴承部位的旋转接触，例如尾轴前后轴承与主轴的接触、推力轴承与主轴的接触、电机等机械部件与主轴的接触等都是电接触，电接触电阻的周期性变化是产生舰船轴频电流的一个重要影响因素[13]。在实验过程中发现当舰船不加电场防护装置即推进轴系不连接电刷时，轴频电流较小，当加入电场防护装置后，推进轴系与电刷连接通过海水和螺旋桨与舰船形成回路，轴频电流明显增大。滑动轴承轴径与电刷的接触如图5所示。

电流在通过金属接触表面的导电斑点时会产生收缩效应从而增加电路的电阻阻值（收缩电阻）c，并且在金属接触表面会形成氧化膜等阻碍电流的表面膜电阻R,这两项电阻之和就是接触电阻，从接触电阻形成的本质可以看出，其阻值的大小会受到接触表面导电斑点的大小、形状、数目和分布的影响。由于每个接触表面在微观上都是凹凸不平的粗糙面，霍姆认为各个凸丘的高度不同，在接触过程中其实只有少数凸丘真正接触并导通流过电流，假定接触表面上流通电流的凸丘都是半径为a的小圆柱，则接触表面总的收缩电阻应为所有实际导通的凸丘电阻值的并联值i与因各个接触的凸丘之间相互影响而造成的电阻值s相串联，即：

式中，为接触面两种物质的平均电阻率，为相互电阻的霍姆半径或点集半径。

在通电以及接触空气过程中，会有一层导电性比较差的膜覆盖在接触表面上。在研究过程中发现接触表面通电时出现氧化膜的情况居多，而大多数氧化膜的电阻率都很高，是一种半导体。氧化膜的硬度一般有别于接触表面的硬度，在相同力的大小下导致接触面积发生改变从而影响接触电阻的大小。由薛定谔方程可知，当接触表面氧化膜层非常薄的时候，如果导电斑点的半径为，则电子穿过其的膜电阻为：

假如在接触表面上接触的凸丘有个，并且凸丘的平均半径为，则总膜电阻为

即接触电阻：

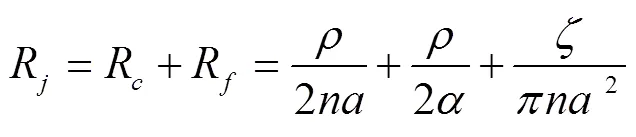
其中，为膜的隧道电阻率。

在实际的工程中接触电阻接触面粗糙情况非常复杂，其中影响其接触的各种因素非常之多，在理论上没有一种精确的模型，格林渥和威灵逊假定[17]，接触表面的凸丘接触情况中接触的凸丘数服从指数分布或是高斯分布，在实验过程中发现，对于大多数接触表面来说，实际情况更倾向于高斯分布。结合图5和式（4）可知轴径沿右侧和左侧电刷方向振动的高度1和2分别为：

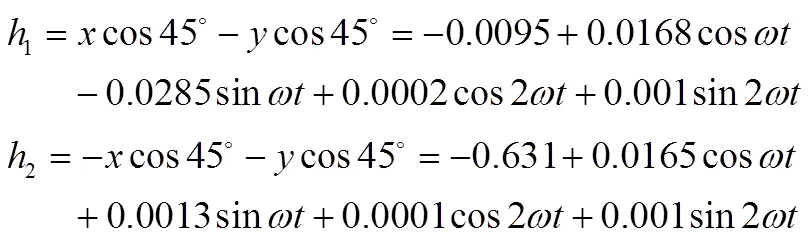
以上述提到的滑动轴承参数为例，假定电刷表面的凸丘均匀分布服从高斯分布，各凸丘之间相互独立，凸丘密度300个/mm2，各凸丘半径相同，=0.01 mm,电刷的接触面积=2cm2，膜的隧道电阻率=5×10-13Wm2，电阻率=9.78×10-8Wm，则右侧电刷与轴径的接触电阻为8（式），式中，、为高斯分布的方差和期望。

同理可得左侧电刷与轴径的接触电阻j2，由图5可知电刷与轴径的总接触电阻是j1和j2并联的结果，则总接触电阻：

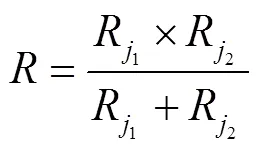
将j1和j2代入即可得总接触电阻的值。当轴径与电刷之间电压为0.1 V时，即可得轴频电流1。

在实际操作过程中发现，由于接触表面的粗糙程度难以掌握，凸丘的个数和大小计算非常困难，故在实际的计算中经常使用下式计算接触表面的电阻。

（9）式中，为接触压力，为与接触形式、压力范围和实际接触点的数目等因素有关的指数，j为与接触材料、表面状况等有关的系数。对于旋转过程中的轴径和轴瓦的中间空隙绝大部分被润滑油充满，轴径与轴瓦的接触面积、导电斑点数和斑点直径难以计算，故采用经验公式，结合文献[13]中给出的公式参数表，取j=0.3,=0.5，将无量纲油膜力代入（9）式可得轴瓦与轴径的接触电阻，根据欧姆定理可计算出流过其上的轴频电流2。由滑动轴承的结构可知，流过滑动轴承的轴频电流为1和2的并联。

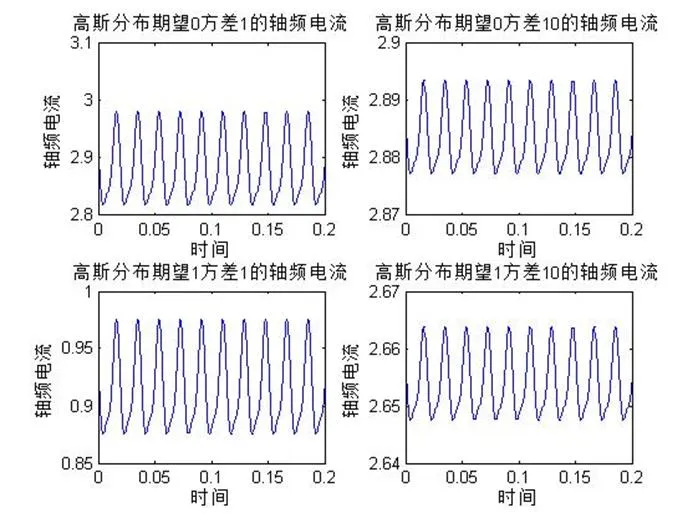
图6在不同的高斯分布下的电刷电流

在对实船进行基于电流补偿的水下静电场防护实验时检测到的轴频电流如图12和13所示，通过滑动轴承轴频电流的仿真与实船轴频电流的对比可以发现，在结果达到了一定程度的吻合，在轴频电流的3倍频以上成分上差距较大，经分析，是由于所建模型为单个滑动轴承模型，与舰船整个轴系的旋转耦合振动模型存在误差，致使整个模型存在部分振动频率的缺失。

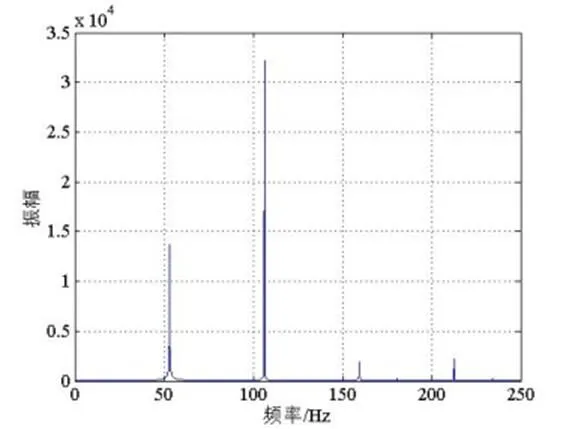
图9轴频电流2的幅频特性

图10 标准高斯分布下轴频电流i随时间的变化

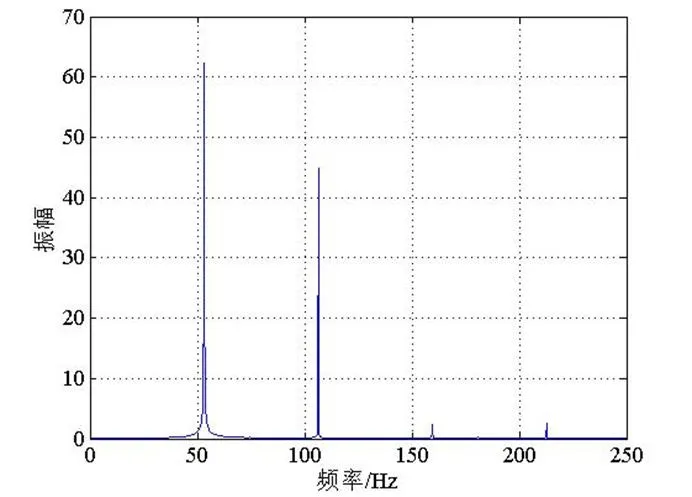
图11 轴频电流i的幅频特性

图13 右轴轴频电流随时间的变化

3 结语

本文主要是对滑动轴承的轴频电流进行了建模和仿真，产生的轴频电流以滑动轴承的旋转频率为基频，同时伴有相应的倍频出现，但倍频电流与基频电流相比较小，所得结果与实际情况具有一定程度的吻合。但是，舰船整个轴系旋转耦合振动非常复杂，如螺旋桨浆叶的叶倍频振动、减速齿轮箱的咬合振动，都会影响轴频电流的大小和频率成分，这方面的分析建模还有待研究。

[1] 林春生．舰船物理场[M].北京:兵器工业出版社,2007:1-3.

[2] 李涛．海水中运动水平时谐电偶极子定位技术研究[D].武汉:海军工程大学，2014：1-10.

[3] Bannister P. The image theory electromagnetic fields of a horizontal electric dipole in the presence of a conducting half space[J]. Radio Science, 1982, 17(5): 1095-1102.

[4] Wait J,Spies K. On the image representation of the quasi-static fields of a line current source above the gound[J] .Can J Phys , 1969 , 47(23):2731-2733.

[5] 卢新城．舰船极低频电场的产生机理及其防护[J].海军工程大学学报，2003（6）：71-74.

[6] 毛伟．浅海环境下运动舰船轴频电磁场建模方法及传播规律研究[D]. 武汉:海军工程大学,2009:20-27.

[7] 李柱国．机械设计与理论[M].北京：科学出版社, 2003：602-627.

[8] 沈小要．转子-轴承-密封系统非线性动力学理论和试验研究[J].噪声与振动控制,2009（6）：67-71.

[9] 杨金福．滑动轴承轴径涡动机理的非线性特性研究[J].动力工程，2005，(25)：562-568.

[10] 陈予恕．非线性转子-轴承系统的分叉[J].振动工程学报,1996（3）:266-275.

[11] Urabe M. Galerkin’s procedure for nonlinear periondic systems. Arch . Rat . Mech . Anal , 1965,20:120-152.

[12] Vrabe M.Reiter A. Numerical computation of nonliear forced oscillations by Galerkin’s procedure.J.Math. Analysis Appic , 1966, 14: 107-140.

[13] 张新勇．滑动轴承油膜涡动及油膜振荡研究[J].太原理工大学学报，2008,（3）：232-235.

Simulation and Modeling of Shaft Frequency Current Based on Vibration Model of Sliding Bearing

Cui Haichao1,Ji Dou1,Li Yang2

(1.College of Electronic Engineering, Naval University of Engineering, Wuhan 430033, China; 2. No 91315 Troops of PLA, Dalian 116041, Liaoning, China)

TP 15

A

1003-4862（2017）11-0001-05

2017-08-15

国家自然科学基金项目（41476153）

崔海超（1989-），男，硕士研究生。研究方向：电磁环境与防护技术。