烃-水体系互溶度预测模型的研究进展
王敏,曹睿,刘艳升,徐泓
烃-水体系互溶度预测模型的研究进展
王敏,曹睿,刘艳升,徐泓
(中国石油大学(北京)重质油国家重点实验室,北京 102249)
在化工、能源、环境、食品和药物等工业设计过程中,真实混合物的可靠溶解度数据非常重要,不仅能丰富相平衡数据库,还能指导工艺设备设计和产品质量控制。本文介绍了烃-水体系相互溶解度的模型化研究,包括状态方程法、活度系数法和经验关联式,以及近年来发展起来的真实溶剂似导体屏蔽模型法(conductor-like screening model for real solvents,COSMO-RS)。状态方程法和活度系数法主要是通过选择非对称的混合规则以及引进描述水分子极性作用的参数,来改善对烃-水体系相互溶解度的计算精度。经验关联式主要是对实验数据的拟合,每种烃的参数不同。COSMO-RS模型根据密度泛函理论(即建立极化电荷密度的简单经验式)计算单个分子嵌入虚拟导体产生的作用,通过准确描述界面统计相互作用获得体系的热力学性质。因此,该方法对各种体系具有普适性。分析表明,COSMO-RS模型对烃-水体系相互溶解度的预测值与实验值吻合良好,可以补充某些难以通过实验获得的烃-水体系互溶度数据。最后总结和展望了烃-水体系相互溶解度模型化的未来发展方向。
烃-水体系;溶解度;真实溶剂似导体屏蔽模型;模型
在化工、能源、环境等工业设计过程中,真实混合物的相平衡数据非常重要[1],其热力学物性及相平衡性质的研究是基础研究的重点及热点之一。物质的溶解度测定及其模型化研究是化工热力学的一个重要分支。
在炼油厂和石化厂,烃-水体系的相互溶解度能够指导工艺设备设计及过程操作。如果水在烃中的溶解度超过其极限,会形成“自由”水相,影响产品质量和设备操作的稳定性,还会造成设备的腐 蚀[2-4]。油中溶解水的量决定了从原油蒸馏塔中拔出水的量,同时水中溶解烃的量是设计水处理系统的重要考量因素。在能源工业的生产、运输及加工过程中,一些溶解的水可能在气相中冷凝,造成设备腐蚀。烃类混合物中水的存在还会导致气体水合物的形成,这会在石油和天然气运输、钻井过程中形成气阻,阻断流体的流动,也会妨碍热量交换器以及膨胀器等装置的运行。预测水在烃混合物中的溶解度可以为防止水相的形成提供参考,使产品符合质量要求。另一方面,炼厂和石油化工厂的废水中不能含有烃类混合物,石油泄漏发生时也需要使烃类混合物远离海水和淡水[5]。建模评估水中的烃类污染物和石油泄漏对环境造成的影响是必需的。由于实验测定的数据有限,烃-水体系溶解度模型化的研究不仅可以丰富数据库,而且可以对化工行业的过程操作和化工动力学提供有效的支持。
1 烃-水体系相互溶解度的研究背景
实验测定是取得相平衡数据最可靠的手段。原则上,所有物质的各种性质都必须通过实验测定来建立物性库。但在工艺过程的设计计算中,全部靠实验测量取得数据并不现实,物质物性的研究费时费资费力。据估计,收集一个气液平衡数据点(比如仅一个二元混合物一个温度和组成下的数据)大约要花费2600美元和两天的时间[6]。此外,由于 烃-水体系的互溶度很小,实验测定常会遇到条件限制,文献中报道的实验数据差异较大,例如,298.15K时水在苯中溶解度摩尔分率的变化范围为0.0026~0.0049[7]。
相平衡研究在化学工程研究领域的重要性是毋庸置疑的,目前相平衡和物性的研究主要通过实验测定和理论预测。实验测定对常规宏观数量级体系基本满足要求,但对强非理想体系并不能达到理想要求,这会限制高纯度要求体系分离技术的发展。在工艺计算中,水在烃中的溶解度比烃在水中的溶解度更重要。当然,烃在水中的溶解度也是环境控制的一个关键问题。
由于水分子中含有氢键,烃-水溶液是强非理想体系,描述烃-水体系的相平衡比较困难。此外,水在烃中的溶解度比烃在水中的溶解度高好几个数量级。烃在水中的溶解度随温度变化先减小后增大,在温度约为300K时烃在水中的溶解度最小;而水在烃中的溶解度是温度的单调函数[8]。
2005年在IUPAC-NIST溶解度数据系列的第81卷中,MACZYNSKI等[7,9-19]编辑整理了之前发表的文献中烃水相互溶解度的实验数据,建立了烃水相互溶解度的数据库,该数据库提供了部分温度下C5~C36的烃与水的相互溶解度数据,并将溶解度数据分为三类,即推荐数据、不确定数据、可疑数据。在模型开发中,只有推荐数据才可以使用。IUPAC给出的C5~C36烃-水体系互溶度的数据误差为±30%,是目前较权威的数据,也是烃-水溶解度模型化研究的主要依据。
2 烃-水体系互溶性研究的模型化方法
2.1 状态方程法
在描述烃-水体系互溶性的模型化研究方法中,最常用的是选用一个立方型状态方程,尝试采用不同的混合规则进行计算。由于水在烃中的溶解度远大于烃在水中的溶解度,使用对称的交互作用参数并不能准确预测烃-水体系的互溶度。1985年,KABADI和DANNER[20]提出了对SRK状态方程采用非对称混合规则计算烃-水体系的互溶度,计算结果优于传统的范德华(vdW)混合规则。1997年,ECONOMOU和TSONOPOULOS[21]证明了对PR状态方程采用Huron-Vidal混合规则,对1-己烯和水体系的相平衡预测结果优于vdW混合规则。2001年,HARUKI等[22-24]提出了对SRK方程采用指数型混合规则,调整了二元作用参数,提高了与实验数据的一致性。
随着水溶液模型的发展,出现了许多用来计算烃-水体系互溶度的理论,例如统计缔合流体理论(statistical associating fluid theory,SAFT)[25-26]和CPA(cubic plus association)状态方程[27-28]。
SAFT状态方程不足以描述水分子的强极性,所以对烃-水体系互溶度的计算并不适用。改进的Lennard-Jones SAFT状态方程(LJ-SAFT)考虑了偶极矩的影响,修改了缔合参数及链参数。1996年,KRASKA等[29]采用改进的LJ-SAFT状态方程预测烃水二元系的溶解度,预测值与实验值表现出更好的一致性,但是它只能应用于计算碳原子数小于9的较轻的烃。2001年GROSS和SADOWSKI[30]提出了以分子为基础的微扰链型统计缔合流体理论(perturbed-chain statistical associating fluid theory,PC-SAFT),该理论使用了一套简化的不同于SAFT模型的组成参数。2006年,GRENNER等[31]使用PC-SAFT理论研究烃-水体系的互溶度,发现该模型可以较准确地计算水在烃中的溶解度,但计算的烃在水中的溶解度远高于实验值。2006年KARAKATSANI等[32]在PC-SAFT理论的基础上考虑了极性项作用,开发了tPC-SAFT模型,可以更好地描述水-正己烷以及水-环己烷体系的相互溶解度。通过调整混合规则和考虑水分子中氢键的影响来增加SAFT理论的复杂性,预测值改善效果有限。
CPA状态方程是KONTOGEORGIS等[33-35]于1996年提出的,是传统SRK方程的延伸,见式(1)~式(3)。



式中,A为A位上没有和其他的活性位结合的分子的分数;ΔAB为A位上的分子与位上的分子的缔合能。
近年来已经有不少学者采用CPA状态方程结合不同的混合规则计算烃-水体系的相平衡和互溶度。2007年,OLIVEIRA等[36]使用CPA状态方程和范德华混合规则计算了烃-水体系的溶解度,结果发现,低温下计算值与实验值的差异略大。由于范德华混合规则不能很好的用于疏水性溶质,2014年MEDEIROS采用KABADI和DANNER提出的混合规则作了改进[37-38],预测结果优于范德华混合规则。目前为止所得到结果表明,在所有的状态关联模型中,CPA状态方程是描述烃-水体系溶解度的最理想模型。
2.2 活度系数法
当达到相平衡时,组分在每相中的逸度相等。只要计算组分在液相中的活度系数,通常可以进行相平衡和溶解度的计算。常见的计算活度系数的方程有NRTL、UNIQUAC和UNIFAC等模型。目前,应用最广泛的是UNIFAC[39-40]以及修正版的UNIFAC(Do)[41]和UNIFAC(LLE)[42]模型。
事实上,原始的UNIFAC模型在预测混合物中含有极性组分(比如水)的无限稀释活度系数时,由于体系的强非理想性,预测效果较差。为了关联不同类型的数据(包括气液平衡和液液平衡),DORTMUND对UNIFAC模型的参数作了修改,即UNIFAC(Do)模型。2006年,JAKOB等[43]采用UNIFAC(Do)模型预测烃-水体系的互溶度,可以得到可靠的烷烃或环烷烃在水中的溶解度数据,但计算时引进了3个没有任何物理意义的经验参数。UNIFAC(Do)模型目前只能计算烷烃和环烷烃在水中的溶解度,而不能计算烯烃和芳香烃在水中的溶解度,也不能计算水在烃中的溶解度。MAGNUSSEN等[44]开发了UNIFAC-LLE模型用于计算烃-水体系的溶解度,但预测偏差较大,并且缺少含环烷烃体系的参数。事实上,现有的UNIFAC类模型,当应用于预测极性混合物(尤其是含水体系)的无限稀释活度系数时,精确度较差。
2013年,SATYRO等[45]提出了基于NRTL方程的无限稀释活度系数模型,来计算不同温度下烃水的互溶度。该模型基于这样一个事实:难溶性混合物的溶解度近似等于无限稀释活度系数的倒数。如式(4)。

无限稀释活度系数如式(5)。




该活度系数模型考察了160种不同的烃在水中的溶解度(964个数据点),烃在水中的绝对平均残差为88%;水在78种不同的烃中的溶解度(621个数据点)的绝对平均残差为34%。这说明了基于NRTL方程的无限稀释活度系数模型能够较准确地预测水在烃中的溶解度,但对烃在水中的溶解度的预测准确性较差。此外,该模型可以与能够更准确代表油品结构特征化的因素相结合[46],来计算油水的相互溶解度。若要更精确地估计水在油相中的溶解度,可以考虑利用更先进的黏度估计方法,例如膨胀流体模型[47]。
液相活度系数F-SAC(functional-segment activity coefficient)模型是无限稀释活度系数法和液液平衡数据的延伸。2016年POSSANI等[48]采用F-SAC模型结合SRK状态方程,使用STAUDT和SOARES[49]提出的SCMR混合规则计算了烃-水体系的互溶度,计算值与实验值吻合,但该模型不能计算碳原子数较多(12以上)的烃与水的互溶度。
以上这些模型能够在一定范围内预测烃水二元系的相平衡和互溶度,但大多数模型都仅适用于298.15K时的一些特定类型的烃-水体系,并且需要根据实验数据回归多个参数。
2.3 经验关联法
美国石油学会(API)整理出版的第9版手册中给出了计算水在纯烃或混合物中溶解度的关联 式[50],见式(9)和式(10)。式(9)表明,在对数坐标系中水在烃中的溶解度与绝对温度的倒数成线性关系。该式适用于计算气-液平衡下水在烃中的溶解度,且只适用于部分给定参数的烃类。当式(9)不适用时,可以用式(10)计算,但式(10)不适用于计算水在烯烃或环烷烃中的溶解度,因为它们的氢碳质量比是个定值。API中给出了温度为298.15K时烃在水中溶解度的关联式,见式(11)。



式中,w为水在烃中的溶解度,摩尔分数;hc为烃在水中的溶解度,摩尔分数;为烃中氢和碳的质量比;为温度,兰氏度(oR);1、2、3分别为特定组分的参数。

表1 298.15K时式(12)中的参数
2001年,TSONOPOULOS[2,8]测定了温度为298.15K时C5~C10水在烷烃、烷基环己烷、1-烯烃、烷基苯与水的相互溶解度,将数据拟合得到关联 式(12)。

式中,、、为参数,与烃的种类有关,部分参数见表1;为碳原子数。
经验关联式存在一些局限性:只适用于部分烷烃(碳原子数小于12)[51];需要知道每种烃对应的参数值,并且参数的确定依赖于分子结构信息[52];通常仅用于25℃。
2.4 COSMO-RS方法
真实溶剂似导体屏蔽模型(conductor-like screening model for real solvents,COSMO-RS)是由KLAMT等[53-56]提出的一种连续介质溶剂化模型。该模型采用量子化学方法(quantum method,QM)计算分子表面间的相互作用,需要参数较少,而且所需的参数不是由实验数据获得。该模型的计算时间较短,与基团贡献法相比,可以区分同分异构体,还考虑了临近效应[6]。因此,COSMO-RS是一种有效的预测流体热力学性质的方法。
COSMO-RS通过式(13)计算溶质在溶剂中的溶解度。
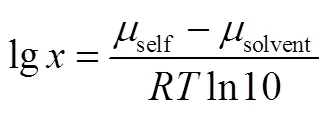
式中,slef为溶质在纯液态中的化学势;solvent为溶质在溶剂中的化学势;为溶解度,摩尔分数;为温度,K。
2003年,KLAMT[57]利用Tsonopoulos测定的烃水溶解度数据对COSMO-RS计算烃-水体系互溶度的可行性作了分析。尽管在COSMO-RS数据库中有烃水的分配系数,但在COSMO-RS参数设置中并没有特别设置溶解度数据的参数。出人意料的是,COSMO-RS对烃-水体系互溶度的计算值与实验值基本吻合,但在两种情况时与实验值差异较大:①温度低于298K时,烃在水中的溶解度;②温度大于473K 时水在烃中的溶解度。
COSMO-RS不仅可以预测烃-水体系的相互溶解度,还可以应用于预测其他的体系。FREIRE等[58]首先实验测定了常压下288.15~318.15K温度范围内水在环状及芳香全氟化物中的溶解度,并用COSMO-RS预测溶解度值,与实验值能较好符合,并说明了温度和结构对溶解度值的影响;此外还预测了水在全氟化物中的摩尔Gibbs自由能和摩尔溶解焓。KAHLEN等[59]用COSMO-RS预测了纤维素在超过2000种离子液体中的溶解度,结果发现阴离子对纤维素溶解度有很大的影响,筛选出醋酸根、癸酸盐类离子液体可以使纤维素溶解度很大。JAAPAR等[60-61]采用COSMO-RS预测了温度为323.15~473.15K时4种主要的具有生物活性的生姜化合物在水中的溶解度,计算结果与实验数据吻合一致。SCHRODER等[62]采用COSMO-RS预测了羧酸在水的中溶解度,证明了COSMO-RS可以预测芳香族羧酸、羟基酸等在水中的溶解度。
3 结语与展望
由于水分子中极强的氢键作用,烃-水体系互溶度的研究需要进一步完善。目前已经具有较为可靠的水在烃中溶解度的预测模型,但还缺乏烃在水中溶解度预测的可靠模型[63-64]。现有的水在烃中溶解度的预测模型一般都只适用于碳原子数小于12的烃,并且适用的温度范围有限。对于结构较复杂的烃与水互溶度的实验数据甚少且不准确。因此未来需要进一步开发更精确、更具有普适性的模型。石化工业中的油品体系往往组成复杂,所以对水与烃混合体系互溶度的研究也是一个重要课题。
烃-水体系的互溶度很低(为mg/kg级),实验测定往往受到限制,理论预测方法比实验方法更容易取得数据,对烃-水体系互溶度的研究很有意义。COSMO-RS是对高度参数化的热力学模型方法的重要补充,同时也是对传统分子动力学(MD)和Monte Carlo(MC)理论的完善和发展。COSMO-RS能够准确地计算烃-水体系的互溶度,但有待调整模型参数,设置依赖于温度的参数,来改善温度低于298K时烃在水中的溶解度和温度大于473K时水在烃中的溶解度的计算。模型的改进需要对分子间作用力的进一步认识,例如考虑氢键对温度的依赖性。
[1] PRAUSNITZ J M,LICHTENTNALER R N,AZEVEDO E G,et al.Molecular thermodynamics of fluid phase equilibria[M].5th ed. State of New Jersey:Prentice Hall,1999.
[2] TSONOPOULOS C.Thermodynamic analysis of the mutual solubilities of normal alkanes and water[J].Fluid Phase Equilibria,1999,156:21-33.
[3] ZHANG W,WILDER J W,SMITH D H.Interpretation of ethane hydrate equilibrium data for porous media involving hydrate-ice equilibria[J].AIChE J.,2002,48:2324-2331.
[4] AVLONITIS D.An investigation of gas hydrates formation energetics[J].AIChE J.,2005,51:1258-1273.
[5] POLAK J,LU B C Y.Mutual solubilities of hydrocarbons and water at 0 and 25℃[J].Chem.,1973,51(24):4018-4023.
[6] 牟天成,JÜRGEN G.真实溶剂似导体屏蔽模型(COSMO-RS)[J]. 化学进展,2008,20(10):1487-1494.
MU T C,JÜRGEN G.Conductor-like screening model for real solvents (COSMO-RS)[J]. Progress in Chemistry,2008,20(10):1487-1494.
[7] MACZYNSKI A,SHAW D G,GORAL M,et al. IUPAC-NIST solubility data series. 81. Hydrocarbons with water and seawater – revised and updated. Part 2. Benzene with water and heavy water[J].Phys. Chem. Ref. Data,2005,34:477-552.
[8] TSONOPOULOS C.Thermodynamic analysis of the mutual solubilities of hydrocarbons and water[J]. Fluid Phase Equilibria,2001,186:185-206.
[9] MACZYNSKI A,SHAW D G,GORAL M,et al. IUPAC-NIST solubility data series. 81. Hydrocarbons with water and seawater – revised and updated. Part 1. C5hydrocarbons with water[J].Phys. Chem. Ref. Data,2005,34:441-476.
[10] MACZYNSKI A,SHAW D G,GORAL M,et al. IUPAC-NIST solubility data series. 81. Hydrocarbons withwater and seawater – revised and updated.Part 3. C6H8–C6H12hydrocarbonswith water and heavy water[J].Phys. Chem. Ref. Data,2005,34:657-708.
[11] MACZYNSKI A,SHAW D G,GORAL M,et al.IUPAC-NIST solubility data series. 81. Hydrocarbons withwater and seawater-revised and updated. Part 4. C6H14hydrocarbons withwater[J]. Phys. Chem. Ref. Data,2005,34:709-53.
[12] MACZYNSKI A,SHAW D G,GORAL M,et al.IUPAC-NIST solubility data series. 81. Hydrocarbons withwater and seawater-revised and updated. Part 5. C7hydrocarbons with waterand heavy water[J].Phys. Chem. Ref. Data,2005,34:1399-487.
[13] MACZYNSKI A,SHAW D G,GORAL M,et al. IUPAC-NIST solubility data series. 81. Hydrocarbons withwater and seawater-revised and updated. Part 6. C8H8–C8H10hydrocarbonswith water[J].Phys. Chem. Ref. Data,2005,34:1489-553.
[14] MACZYNSKI A,SHAW D G,GORAL M,et al. IUPAC-NIST solubility data series. 81. Hydrocarbons withwater and seawater revised and updated. Part 7. C8H12–C8H18hydrocarbonswith water[J].Phys. Chem. Ref. Data,2005,34:2261-2298.
[15] MACZYNSKI A,SHAW D G,GORAL M,et al. IUPAC-NIST solubility data series. 81. Hydrocarbons withwater and seawater – revised and updated. Part 8. C9hydrocarbons withwater[J].Phys. Chem. Ref. Data,2005,34:2299-345.
[16] MACZYNSKI A,SHAW D G,GORAL M,et al. IUPAC-NIST solubility data series. 81. Hydrocarbons withwater and seawater – revised and updated. Part 9. C10hydrocarbons withwater[J].Phys. Chem. Ref. Data,2006,35:93-151.
[17] MACZYNSKI A,SHAW D G,GORAL M,et al.IUPAC-NIST solubility data series. 81. Hydrocarbons withwater and seawater – revised and updated. Part 10. C11and C12hydrocarbons with water[J].Phys. Chem. Ref. Data,2006,35:153-203.
[18] SHAW DG,MACAYNSKI A,GORAL M,et al.IUPAC-NIST solubility data series. 81. Hydrocarbons withwater and seawater – revised and updated. Part 11. C13–C36hydrocarbonswith water[J].Phys. Chem. Ref. Data,2006,35:687-784.
[19] SHAW D G,MACAYNSKI A,HEFTER G T,et al.IUPAC-NIST solubility data series. 81. Hydrocarbons with water and seawater– revised and updated. Part 12. C5–C26hydrocarbons with seawater[J].Phys. Chem. Ref. Data,2006,35:785-838.
[20] KABADI V N,DANNER R P.A modified Soave–Redlich–Kwong equation of state for water hydrocarbon phase equilibria[J].Ind. Eng. Chem. Process Des. Dev.,1985,24:537-541.
[21] ECONOMOU I G,TSONOPOULOS C.Associating models and mixing rules in equations of state for water/hydrocarbon mixtures[J].Chem. Eng. Sci.,1997,52:511-525.
[22] SHIN H Y,HARUKI M,YOO K P,et al.Phase behavior of water + hydrocarbon binary systems by using multi-fluid nonrandom lattice hydrogen bonding theory[J].Fluid Phase Equilibria,2001,189:49-61.
[23] HARUKI M,IWAI Y,ARAI Y.Prediction of phase equilibria for the mixtures containing polar substances at high temperatures and pressures by group contribution equation of state[J].Fluid Phase Equilibria,2001,189:13-30.
[24] HARUKI M,IWAI Y,NAGAO S,et al.Measurement and correlation of liquid–liquid equilibria for water + aromatic hydrocarbon binary systems at high temperatures and pressures[J].Chem. Eng. Data,2001,46:950-953.
[25] 李进龙,何昌春,彭昌军,等.基于化学缔合统计理论的链状流体状态方程[J].中国科学(化学),2010(9):1198-1209.
LI J L,HE C C,PENG C J,et al.A chain of fluid state equation based on the theory of chemical association statistics[J].Chinese Science(Chemistry),2010(9):1198-1209.
[26] HEMPTINNE DE J C,MOUGIN P,BARREAU A,et al.Application to petroleum engineering of statistical thermodynamics–based equations of state[J].Oil & Gas Science and Technology—Rev. IFP,2006,61(3):363-386.
[27] KONTOGEORGIS G M,MICHELSENM L,FOLAS G K,et al.Ten years with the CPA (cubic-plus-association) equation of state. part 1. Pure compounds and self-associating systems[J].Ind. Eng. Chem. Res.,2006,45:4855-4868.
[28] KONTOGEORGIS G M,MICHELSEN M L,FOLAS G K,et al.Ten years with the CPA (cubic-plus-association) equation of state.part 2. Cross-associating and multicomponent systems[J].Ind. Eng. Chem. Res.,2006,45:4869-4878.
[29] KRASKA T,GUBBINS K E. Phase equilibria calculations with a modified SAFT equation of state. 1. Pure alkanes,alkanols,and water[J].Ind. Eng. Chem. Res.,1996,35:4738-4746.
[30] GROSS J,SADOWSJI G.. Application of the perturbed-chain SAFT equation of state to associating systems[J]. Ind. Eng. Chem. Res.,2002,41:5510-5515.
[31] GRENNER A,SCHMELZER J,SOLMS N V,et al.Comparison of two association models (elliott-suresh-donohue and simplified PC-SAFT) for complex phase equilibria of hydrocarbon-water and amine-containing mixtures[J].Ind. Eng. Chem. Res.,2006,45:8170-8179.
[32] KARAKATSANI E K,KONTOGEORGIS G M,ECONOMOU I G,et al.Evaluation of the truncated perturbed chain-polar statistical associating fluid theory for complex mixture fluid phase equilibria[J].Ind. Eng. Chem. Res.,2006,45:6063-6074.
[33] KONTOGEORGIS G M,VOUTSAS E C ,YAKOUMIS I V,et al.An equation of state for associating fluids[J].Ind. Eng. Chem. Res.,1996,35:4310-4318.
[34] KONTOGEORGIS G M,YAKOUMIS I V,MEIJER H,et al. Multicomponent phase equilibrium calculations for water–methanol– alkane mixtures[J].Fluid Phase Equilibria,1999,158/159/160:201-209.
[35] YAN W,GEORGIOS M,KONTOGEORGIS G M,et al.Application of the CPA equation of state to reservoir fluids in presence ofwater and polar chemicals[J].Fluid Phase Equilibria,2009,276:75-85.
[36] OLIVEIRA M B,COUTINHO J A P,QUEIMADA A J.Mutual solubilities of hydrocarbons and water with the CPA EoS[J].Fluid Phase Equilibria,2007,258(1):58-66.
[37] MEDEIROS M.Mutual solubilities of water and hydrocarbons from the cubic plus association equation of state:a new mixing rule for the correlation of observed minimum hydrocarbon solubilities[J]. Fluid Phase Equilibria,2014,368:5-13.
[38] KABADI V N,DANNER R P,A modified Soave-Redlich-Kwong equation of state for water-hydrocarbon phase equilibria[J].Ind. Eng. Chem. Process Des. Dev.,1985,24:537-541.
[39] FREDENSLUND A ,GMEHLING J,RASMUSSEN P.Vapor-liquid equilibria using UNIFAC [R].Amsterdam:Elsevier,1977.
[40] 刘洪勤,高崇侠,赵新亮.无限稀释活度系数的预测模型[J].高校化学工程学报,1996(1):9-16.
LIU HQ,GAO C X,ZHAO X L.Prediction model of infinite dilution activity coefficient[J].Journal of Chemical Engineering,1996(1):9-16.
[41] GMEHLING J,LI J D,SCHILLER M A.A modified UNIFAC model. 2. Present parameter matrix and results for different thermodynamic properties[J].Ind. Eng. Chem. Res.,1993,32(1):178-193.
[42] LARSEN B L,RASMUSSEN P,FREDENSLUND A.A modified UNIFAC group-contribution model for prediction of phase equilibria and heats of mixing[J].Ind. Eng. Chem. Res.,1987,26 (11):2274-2286.
[43] JAKOB A,GRENSEMANN H,LOHMANN J,et al.Further development of modified UNIFAC(Dortmund):revision and extension 5[J].Ind. Eng. Chem. Res.2006,45(23):7924-7933.
[44] MAGNUSSEN T,RASMUSSEN P.UNIFAC parameter table for prediction of liquid-liquid equilibriums[J].Industrial & Engineering,1981,20(2):331-339.
[45] SATYRO M A,SHAW J M,YARRANTON H W.A practical method for the estimation of oil and water mutual solubilities[J]. Fluid Phase Equilibria,2013,355:12-25.
[46] LORIA H,HAY G,SATYRO M A.Thermodynamic modeling and process simulation through PIONA characterization[J].Energy & Fuels,2013,27(6):3578-3584.
[47] YARRANTON H W,SATYRO M A.Expanded fluid based viscosity correlation for hydrocarbons[J].Ind. Eng. Chem. Res.,2009,48(7):3640-3648.
[48] POSSANI L F K,STAUDT P B,SOARES R D P.Prediction of water solubilities in hydrocarbons and oils using F-SAC coupled with SRK-EoS[J].Fluid Phase Equilibria,2016,427:394-405.
[49] STAUDT P B,SOARES R D P. A self-consistent Gibbs excess mixing rule for cubic equations of state[J].Fluid Phase Equilibria,2012,334:76-88.
[50] API Technical data book:petroleum refining[M].9th ed.Washington (DC):American Petroleum Institute,2013.
[51] HEMPTINNE DE J C,LEDANOIS J M,MOUGIN P,et al.Select thermodynamic models for process simulation——A practical guide using a three steps methodology[M].Editions Technip,2012.
[52] BRADY C J,CUNNINGHAM J R,WILSON G M. Water– hydrocarbon liquid–liquid–vapor equilibrium measurements to 530 F̊[R]. Gas Processors Association Research Report,1982.
[53] KLAMT A.Conductor-like screening model for real solvents:a new approach to the quantitative calculation of solvation phenomena[J]. The Journal of Physical Chemistry,1995,99(7):2224-2235.
[54] KLAMT A.Refinement and parametrization of COSMO-RS[J].The Journal of Physical Chemistry A,1998,102(26):5074- 5085.
[55] KLAMT A,ECKERT F.COSMO-RS:a novel and efficient method for the a priori prediction of thermophysical data of liquids[J].Fluid Phase Equilibria,2000,172(1):43-72.
[56] ECKERT F,KLAMT A.Fast solvent screeningquantum chemistry:COSMO-RS approach[J].AIChE Journal,2002,48(2):369-385.
[57] KLAMT A.Prediction of the mutual solubilities of hydrocarbons and water with COSMO-RS[J].Fluid Phase Equilibria,2003,206:223–235.
[58] FREIRE M G,CARVALHO P J,SANTOS L M N B F,et al.Solubility of water in fluorocarbons:experimental and COSMO- RS prediction results[J]. Journal of Chemical Thermodynamics,2010,42(2):213-219.
[59] KAHLEN J,MASUCH K,LEONHARD K. Modelling cellulose solubilities in ionic liquids using COSMO-RS[J]. Green Chemistry,2010,12(12):2172-2181.
[60] JAAPAR S Z S,IWAI Y,MORAD N A.Effect of-solvent on the solubility of ginger bioactive compounds in water using COSMO-RS calculations[J].Applied Mechanics and Materials,2014(624):174-178.
[61] JAAPAR S Z S,MORAD N A,IWAI Y.Solubilities prediction of ginger bioactive compounds in liquid phase of water by the COSMO-RS method[M]//Recent trends in physics of material science and technology,Springer Singapore,2015:337-352.
[62] SCHRODER B,SANTOS L M N B F,MARRUCHO I M.Prediction of aqueous solubilities of solid carboxylic acids with COSMO-RS[J]. Fluid Phase Equilibria,2010(289):140-147.
[63] VIDAL J.Thermodynamics – applications in chemical engineering and the petroleum industry[M].Paris:Editions Technip,2003.
[64] SATYRO M A.The role of thermodynamic modeling consistency in process simulation[C]//8th World Congress of Chemical Engineering,Palais des Congres,Montreal,2009.
Progress on prediction models of mutual solubility of hydrocarbon-water system
WANG Min,CAO Rui,LIU Yansheng,XU Hong
(State Key Laboratory of Heavy Oil,China University of Petroleum,Beijing 102249,China)
In chemical engineering,energy,environment,food and medical industry,reliable solubility data for real mixture is very important for process design,which can not only enrich the database of phase equilibrium,but also be greatly helpful for the design of process device and the fine control of products quality. It introduces the model of the mutual solubility on hydrocarbon-water system,including state equation methods,activity coefficient methods,empirical correlations and COSMO-RS(conductor-like screening model for real solvents) model developed in recent years. The state equation methods and activity coefficient methods are usually employed to improve the accuracy of the mutual solubility on hydrocarbon-water system according to the asymmetric mixing rules and the adjustment of the parameters describing the polarity of water molecules. The empirical correlations are mainly used to fit the experimental data,where the parameters of the correlations are different with respect to particular hydrocarbon system. Furthermore,the COSMO-RS model calculates the single molecule embedded virtual conductor based on the density functional theory by which the simple empirical polarization charge density is established. It is efficient and accurate for describing the statistical thermodynamic interactions of interface,and thus the features of thermodynamic qualities can be grasped conveniently. The results indicate that the predicted data of COSMO-RS model agrees well with the experimental one,which show the universality of COSMO-RS model in various kinds of systems,and thus providing an easy method for complementing the unmeasurable experimental data of mutual solubility for hydrocarbon-water system. The future directions for prediction models of the mutual solubility on hydrocarbon-water system are proposed.
hydrocarbon-water system;solubility;COSMO-RS;model
TQ013.1;O645.12
A
1000–6613(2017)12–4343–07
10.16085/j.issn.1000-6613.2017-0322
2017-02-27;
2017-04-06。
国家自然科学基金项目(21576287,21176248)。
王敏(1991—)女,硕士研究生,研究方向为油水互溶度的研究。E-mail:1070539920@qq.com。
曹睿,副教授,研究方向为精馏工艺、设备开发及应用基础研究。E-mail:ctray@ cup.edu.cn。

