给“猜想”一个名分——基于一类多元求最值问题的探讨

江苏 张路民

给“猜想”一个名分
——基于一类多元求最值问题的探讨

江苏 张路民

一、问题提出

二、寻因索果

果然比较实用，但如何让学生信服，或者这其中到底有怎样的关联呢？是不是适用于所有问题？带着这些疑问，笔者对其进行了进一步的研究.

首先，笔者对原题的解法进行了研究，希望能从中发现问题所在.

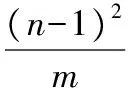
三、建构模式

从上述的分析可以看出这一“猜想”其实是偶然中的“必然”(当然也可能会出现例外，没有理论依据).基于这样的特征和普遍性，笔者觉得有必要向学生作一个推广，在遇到类似问题且又找不到方法的情况下可以尝试.当然，毕竟是猜想肯定会有一定的风险和偶然性.为了方便记忆，笔者给具备这种类型的表达式起了个名字叫“轮换对称式”.顾名思义，这类问题的特征是变量可以互换且结构上是对称的(即交换后不影响结果).解决策略是：假设两个变量相等，代入后得到值即可能为所求最值.

四、问题延伸

有一些问题可能从题面上看不具备“轮换对称式”的特征，需要作适当的变形处理方能满足，比如：

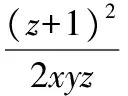
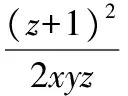
上述两个例子进一步验证了这种“猜想”具有一定的普遍性，但有些问题需要进行适当的变形处理.

五、高考应用

为了进一步推广这种猜想，笔者又尝试着解决了两道高考试题看看是否具有普遍推广性.

六、反例

【例4】(2016·江苏卷·14)在锐角三角形ABC中，若sinA=2sinBsinC，则tanAtanBtanC的最小值是________.

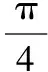
由此可见，猜想毕竟只是猜想，不一定适用于所有的题目，还不能作为真命题存在.但是我们也看到它终究是适用于大多数此类题型的，在找不到更好的方法的情况下，也不失为一种较好的解决填空题的策略.

江苏省南京市大厂高级中学)