概率易错解 根源找出来

安徽 华腾飞

概率易错解 根源找出来

安徽 华腾飞

概率是中学数学的重要知识点，也是各地高考的考点，同时更是同学们的易错点．为了减少同学们求解此类问题的出错率，提高解题技能与技巧，下面就同学们容易出现的典型错解举例剖析，希望能够引起同学们的高度注意．

一、将“非等可能”与“等可能”混同致错

例1将一枚硬币连掷三次，出现“2个正面1个反面”的概率是多少？

剖析错解1错在事件“3正、2正一反、1正2反、3反”不是等可能事件．事实上，一枚硬币连掷三次有8种等可能事件：(正、正、正)、(正、正、反)、(正、反、正)、(反、正、正)、(正、反、反)、(反、正、反)、(反、反、正)、(反、反、反)．错解2错在“2正1反”并不是一种结果，而是三种结果：(正、正、反)、(正、反、正)、(反、正、正)．

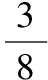
二、将“互斥”与“独立”混同致错

例2某家庭电话在家中有人时，打进的电话响第一声时被接的概率为0.1，响第二声时被接的概率为0.3，响第三声时被接的概率为0.4，响第四声时被接的概率为0.1，那么电话在响前四声内被接的概率是多少？

错解设电话响第一声时被接的概率为P(A1)=0.1；电话响第二声时被接的概率为P(A2)=0.3；电话响第三声时被接的概率为P(A3)=0.4；电话响第四声时被接的概率为P(A4)=0.1．所以电话在响前四声时被接的概率为

P=P(A1)·P(A2)·P(A3)·P(A4)=0.1×0.3×0.4×0.1=0.001 2．

剖析上述错解的原因在于把互斥事件当成相互独立同时发生的事件来考虑．根据实际生活经验，电话在响前四声内，响每一声时是否被接彼此互斥．

正解P=P(A1)+P(A2)+P(A3)+P(A4)=0.1+0.3+0.4+0.1=0.9．

例3两个篮球运动员在罚球线投球的命中率分别是0.7和0.6，每人投球3次，试计算两人都恰好投进2球的概率．

错解设“甲恰好投进2球”为事件A，“乙恰好投进2球”为事件B，则两人都恰好投进两球为A+B．故此可得，

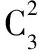
剖析上述错解的原因在于将相互独立同时发生的事件当成互斥事件来考虑，将两人都恰好投中2球理解为“甲恰好投中2球”与“乙恰好投中2球”的和．

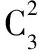
三、将“互斥”与“对立”混同致错

例4从装有2个红球与2个白球的口袋内任取两个球，那么互斥而不对立的两个事件是

( )

A.至少有1个白球与都是白球

B.至少有1个白球与至少有一个红球

C.恰有1个白球与恰有2个白球

D.至少有1个白球与都是红球

错解选B．

剖析上述错解的原因在于把“互斥”与“对立”混为一谈，要准确地解答此类问题，应弄清楚对立事件与互斥事件的联系与区别，表现在以下三个方面：

(1)两事件对立，必定互斥，但互斥事件未必对立；

(2)互斥的概念适用于多个事件，但对立概念只适用于两个事件；

(3)两个事件互斥只表明这两个事件不能同时发生，即至多只能发生其中一个，但可以不发生；而两事件对立则表示它们有且仅有一个发生．

正解选项A，B中两事件不互斥，当然也不对立；选项C中两事件互斥但不对立；选项D中两事件不仅互斥而且对立．故选C．

四、将“有序”与“无序”混同致错

例5从10件产品(其中次品3件)中，一件一件地不放回地任意取出4件，求4件中恰有1件次品的概率．

错解因为第一次取有10种取法，第二次取有9种取法，第三次取有8种取法，第四次取有7种取法，则由乘法原理可知，从10件中取出4件，共有10×9×8×7种取法，故样本空间S含有10×9×8×7个基本事件．

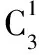
剖析计算样本空间S所含基本事件的个数是用排列的方法，即考虑了抽取的顺序，而计算事件A所包含的基本事件个数时是用组合的方法，即没有考虑抽取的顺序．

正解(1)用排列的方法

(2)用组合的方法

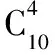
五、将“放回”与“不放回”混同致错

例6 一个袋中装有4个黑球、1个白球，现从袋中每次摸出一球，然后再放回袋中，求第3次摸球时首次摸到白球的概率．

剖析上述错解将有放回问题当成无放回问题来处理．有放回相当于做重复试验，其他条件完全相同；无放回则是做不同的试验，即后一次试验与前一次试验的条件不同，是在新的标准下进行的．由于两种情况的结果不一样，所以混淆会导致错误的发生．

安徽省灵璧县黄湾中学)