转子系统不平衡故障的再现方法浅析

叶瑞夺，王丽萍，罗 忠，王德友，刘永泉

（1.东北大学机械工程与自动化学院，沈阳110819；2.中国航发沈阳发动机研究所，沈阳110015）

转子系统不平衡故障的再现方法浅析

叶瑞夺1，王丽萍1，罗 忠1，王德友2，刘永泉2

（1.东北大学机械工程与自动化学院，沈阳110819；2.中国航发沈阳发动机研究所，沈阳110015）

针对转子系统不平衡特征再现设计问题，提出1种基于动力学相似关系的模型再现方法。根据转子系统的振动微分方程，通过积分模拟法和量纲分析法建立转子系统中转轴、转盘、弹性支承和不平衡量的相似关系。根据相似关系，设计了原型不平衡转子系统的动力学相似模型，利用有限元方法仿真验证了所得相似关系的正确性。试验采用最小二乘三点法识别原型与模型不平衡转子试验台的不平衡量，给出再现原型不平衡特征的过程，验证了不平衡特征再现设计方法的有效性。总结了基于动力学相似关系的转子系统不平衡特征再现设计方法。

转子系统；不平衡；动力学相似；故障再现；模型试验；大型旋转机械

0 引言

在航空发动机等大型旋转机械中，转子不平衡是1种常见现象，是指转子轴向各截面的质心不都在回转中心线上，直接影响旋转机械的工作稳定性与安全性。因此掌握转子系统不平衡振动机理非常重要。研究转子系统的不平衡振动机理，仅靠理论解析和数值仿真不足以解决实际问题，必须结合物理试验[1-3]。然而，直接进行原型试验存在试验成本高、周期长、难度大等局限，因此相似模型试验是常用的研究手段[4]。通过利用相似模型研究、预测原型转子系统的不平衡振动机理，为原型转子系统平衡方案的选择和减振技术的验证提供低成本、短周期、低危险性的试验方案尤为必要。

学者们在转子系统相似理论研究和不平衡故障研究领域做了大量工作，而对转子系统不平衡故障的动力学相似理论研究尚不多见。Wu[5]建立了转子系统的完全相似模型，并验证了相似关系的正确性；Baxi[6]利用方程分析法建立了汽轮发电机轴系的动力学相似模型，复现了原型系统的动力学特性；李淑莲[7]提出了基于全息谱分析的转子系统不平衡量识别方法；Nelson[8]在考虑转子系统陀螺力矩、外阻尼等因素的基础上，建立了转子系统的有限元模型；罗忠[9]等采用量纲分析与方程分析相结合的方法，着重分析了轴承参数对固有特性模型试验预测结果的影响。

本文基于动力学相似理论，以模型试验预测原型转子系统不平衡振动机理为背景，在建立转子系统动力学相似关系的基础上，提出再现转子系统不平衡故障的动力学相似模型设计方法，并进行了数值仿真和试验验证。

1 动力学相似关系

1.1 振动方程

为简化说明，建立带不平衡量的转子系统如图1所示。系统由转轴、转盘和弹性支承构成。O为转盘的质心，转盘存在质量偏心，从而引起转子不平衡。建立oxyz坐标系，以o为坐标原点，转轴中心线为x轴，y轴水平垂直于x轴，z轴竖直垂直于x轴。转轴直径为d，长度为l；转盘宽度为L，外径为D；系统转速为ω。

式中：E为转轴材料弹性模量；I为转轴截面矩；γ为合成挠度；a为转盘的单位长度质量相对于旋转轴的转动惯量；t为时间；i为虚数单位；m为转轴单位长度的质量；p=me1ω2为单位长度不平衡力，e1为不平衡度。

为完整表达转子系统的动力学方程，应补充转轴中心线的倾角α和法向应力σ的表达式

式中：M为弯矩；W为转轴抗弯截面系数。

1.2 动力学相似关系推导

运用积分模拟法，将式（1）、（2）中所有导数用相应量的比值表示，即去掉所有微分符号，沿各轴的分量用量本身来代替，坐标用定性尺寸来代替，即分别用γ/l2、γ/l、γ/t2、γ/t代替 ∂2γ/∂l2、∂γ/∂l、∂2γ/∂t2、∂2γ/∂t，转换为

式中：πi（i=1,2,…,7）为相似准则；下标m表示模型，p表示原型。

通过量纲分析，式（7）中各变量的量纲存在如下关系

式中：[ε]为变量ε的量纲；G为转轴重力；ρ为转轴密度；Jp为转盘的质量惯性矩。

利用式（8）对式（7）进行整理得

选用独立变量d、l、E、ρ的相似比表示其余参数的相似比。根据式（9）中的相似关系，结合量纲分析，推导转子系统部分参数的相似比为

式中：λε(ε=G,ω,ρ,g,d,l,E,γ,e1,u,α,σ,D,L)，为参数的相似比；u为不平衡量。

忽略转盘的轴向变形，主要考虑其质量和质量惯性矩为

式中：M为转盘质量；ρd为转盘材料密度。

计算得到转盘质量和质量惯性矩的相似比为

式中：M0为弹性支承的参振质量；y为弹性支承位移；K为弹性支承刚度；Q为弹性支承受到的转子不平衡力。

运用积分模拟法，根据式（15）得到相似准则为

弹性支承的受力和位移是与转子相互作用产生的，所以其不平衡力的相似比等于转子系统中力的相似比；弹性支承位移的相似比等于转轴挠度的相似比。即 λQ=λG，λy=λγ。结合式（10），根据式（17）求得弹性支承刚度的相似比为

式（10）、（14）和（18）组成转子系统的整体相似关系。

2 数值仿真验证

为验证相似关系的正确性，给出如图1所示转子系统作为原型，按相似关系设计模型转子系统进行仿真验证。原型材料参数见表1，结构参数见表2，弹性支承刚度为3×107N/m。

表1 原型转子系统材料参数

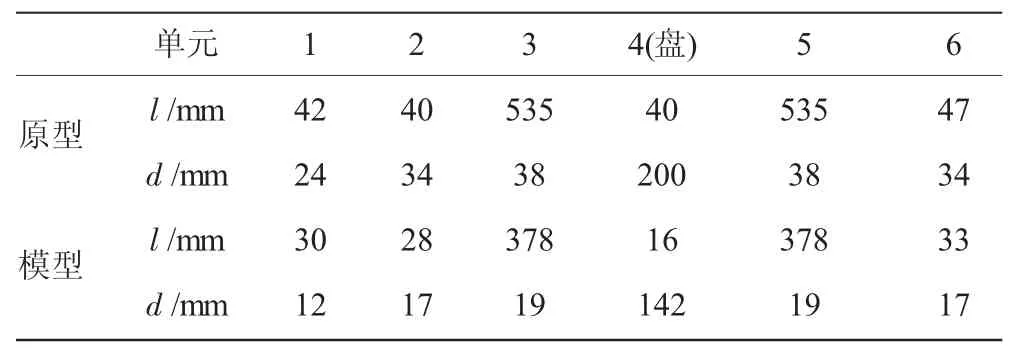
表2 原型与模型转子系统结构参数

将不平衡响应相似比 作为模型转子系统的设计准则。模型采用与原型相同材料，选定转轴长度相似比 λy=/2，转轴直径相似比 λd=0.5，其余参数相似比通过式（10）、（14）和（18）确定。按相似关系得到模型结构参数，见表2，弹性支承刚度为5.3×106N/m。

采用有限元方法对存在不平衡量的转子系统进行数值仿真。首先对转子系统划分单元，如图2所示。单元的质量、刚度、比例阻尼和陀螺力矩的矩阵参见文献[8]和[11]，通过各单元的参数矩阵将转子系统组集起来。

通过MATLAB编写仿真程序，设定原型不平衡量为up=2000 g·mm，则模型不平衡量应为

为便于研究，根据转速相似比λω=1，选取原型与模型转速均为1000 r/min工况下节点9处的不平衡特征进行分析，获得轴心轨迹和时域响应，分别如图3、4所示。

仿真原型与模型节点9处的轴心轨迹近似于椭圆，时域响应为正弦波形，符合不平衡现象的判定规则[12]。

提取图4中时域响应水平和垂直方向的平均不平衡响应幅值，见表3。误差在容许范围内，而且原型与模型的轴心轨迹高度吻合，满足不平衡响应相似比λγ=1的相似设计要求。数值仿真说明所得相似关系是正确的，且可以通过动力学相似模型再现转子系统的不平衡特征并预测原型不平衡响应。

表3 仿真原型与模型平均不平衡响应幅值

3 试验验证

为进一步检验相似关系的正确性和通过动力学相似模型再现转子系统不平衡特征的可行性，需进行试验。试验原型材料参数见表1，结构参数见表2，弹性支承刚度为3×107N/m。采用相同材料，按表2参数搭建模型转子系统试验台。

采用自建测试系统测量转子系统的不平衡响应，系统由cDAQ9188机箱与NI9229采集卡及基于Lab VIEW的采集软件组成。所用电涡流位移传感器为联能CWY-DO-502，灵敏度为4 mV/um。

3.1 不平衡量识别

通过模型再现原型转子系统的不平衡特征，需首先识别二者的不平衡量，然后将模型不平衡量改造成与原型不平衡量满足相似关系的大小。原型试验台的传感器布置如图5所示，采用挠性联轴器将转子系统与电动机相连，避免引入电动机的振动特性。

采用最小二乘三点法[13]识别转子系统不平衡量。过程如下：未加试重时，转子系统存在原始不平衡量ux，相位角为θx，在测试面测出转子系统的不平衡响应振幅Ax。然后先后3次分别在θi(i=1,2,3)等于0°、120°和240°方向加均为u0的试重，设由u0引起的不平衡响应振幅为A0。3次测得不平衡响应合振幅为A01、A02和 A03，令=/1(i=1,2,3)，则不平衡量相位角为

转速为1000 r/min时，测得原型试验台未加试重和3次加试重后的不平衡响应，见表4。根据表4中数据计算出原型试验台的不平衡量为3169 g·mm＜77.04°。

表4 原型转子系统不平衡响应幅值

模型试验台传感器布置如图6所示，传感器在轴向位置与原型中传感器的轴向位置满足转轴长度相似关系。同样采用挠性联轴器将模型转子系统与电动机相连，避免引入电动机的振动特性。

转速为1000 r/min时，测得模型试验台未加试重和3次加试重后的不平衡响应，见表5。根据表5中的数据计算出模型转子系统的不平衡量为1354 g·mm＜-56.71°，负号表示与转速反向。

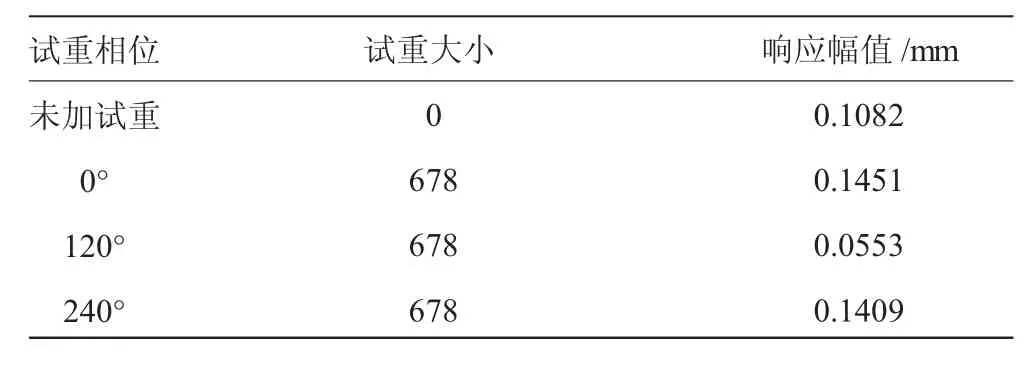
表5 模型转子系统不平衡响应幅值

3.2 不平衡相似试验

原型试验台转子的不平衡量为3169 g·mm＜77.04°，根据相似关系计算模型试验台应再现的不平衡量为

将模型试验台的不平衡量由1354 g·mm改造为560 g·mm，改造方法是在转盘上不平衡量方向的反向打孔处加配重，配重大小由需要抵消的不平衡量和打孔位置的半径决定。配重须抵消的不平衡量大小为

模型不平衡量满足相似设计要求后，分析转速为时原型与模型试验台节点9处的不平衡特征，轴心轨迹和时域响应分别如图7、8所示。

原型试验台轴心轨迹近似于“8字形”，时域响应近似于M波形，说明原型试验台存在一定程度的不对中，会对不平衡响应造成影响[14]。根据文献[15]所得结论：不对中故障对转子系统不平衡响应的影响主要发生在临界转速附近，在工作转速时，这种影响很小。转子系统的工作转速为1000 r/min，远小于转子系统试验台的临界转速2128 r/min，故可认为原型试验台的不对中故障对其不平衡响应影响很小。

根据时域响应计算出二者的平均不平衡响应幅值见表6，误差在允许范围内。对比图7中原型与模型节点9处的轴心轨迹可知，二者并不充分吻合，但从轴心轨迹所处范围和时域响应幅值可认为，原型与模型试验台的不平衡响应幅值近似相等，满足相似设计要求。试验进一步验证了相似关系的正确性，同时也证明了通过动力学相似模型再现转子系统不平衡特征并预测原型不平衡响应是准确有效的。

表6 试验原型与模型平均不平衡响应幅值

综上所述，提出基于动力学相似模型的转子系统不平衡特征再现设计方法。

（1）选定制造相似模型的材料，确定材料密度相似比λρ和弹性模量相似比λE。根据不平衡特征再现设计要求和模型尺寸要求，结合式(10)、(14)和(18)推导其余参数相似比，并搭建相似模型；

（2）识别原型与模型转子系统不平衡量，结合式（23）将模型不平衡量改造成与原型满足相似关系的大小。

4 结论

（1）采用积分模拟法和量纲分析法，给出了不平衡转子系统动力学相似关系的推导过程，并结合数值仿真和试验验证了相似关系的正确性。

（2）基于动力学相似模型，提出了转子系统不平衡特征再现和不平衡响应模型试验预测的方法。

（3）试验能够获得转子系统相对准确的轴心轨迹和振动响应，而数值仿真只能获得理想故障模式下的振动情况，可用试验结果指导数值仿真的修正与完善。

[1]Bladh R,Pierre C,Castanier M P,et al.Dynamic response predictions for a mistuned industrial turbo machinery rotor using reduced-order modeling[J].Journal of Engineering for Gas Turbines and Power,2002,124(2):311-324.

[2]王桂华,蔚夺魁,洪杰,等.航空发动机可靠性试验方法研究[J].航空发动机,2014,40(5):13-17.WANG Guihua,YU Duokui,HONG Jie,et al.Reliability test method of aeroengine[J].Aeroengine,2014,40(5):13-17.（in Chinese）

[3]Chacartegui R,Sánchez D,Mu?oz A,et al.Real time simulation of medium size gas turbines[J].Energy Conversion and Management,2011,52(1):713-724

[4]王有,罗忠,曲涛,等.薄壁构件试验模型的动力学相似设计方法[J].航空发动机,2016,42(1):32-36.WANG You,LUO Zhong,QU Tao,et al.Dynamic similitude design method of experimental models for thin walled structures[J].Aeroengine,2016,42(1):32-36.（in Chinese）

[5]Wu J J.Prediction of lateral vibration characteristics of a full-size rotor-bearing system by using those of its scale models[J].Finite Elements in Analysis and Design,2007,43(10):803-816.

[6]Baxi C B,Telengator A,Razvi J.Rotor scale model tests for power conversion unit of GT-MHR [J].Nuclear Engineering and Design,2012,251(10):344-348.

[7]刘淑莲,李强,郑水英.基于全息谱分析的非线性转子系统不平衡量识别[J].机械工程学报,2010,46(17):62-67.LIU Shulian,LI Qiang,ZHENG Shuiying.Unbalance identification of nonlinear rotor system based on holospectrum analysis[J].Journal of Mechanical Engineering,2010,46(17):62-67.（in Chinese）

[8]Nelson H D,McVaugh J M.The dynamics of rotor-bearing systems using finite elements[J].Journal of Manufacturing Science and Engineering,1976,98(2):593-600.

[9]罗忠,闫宇龙,韩清凯,等.转子-轴承系统的动力学相似及其轴承参数的影响分析[J].振动与冲击,2012,31(S):12-16.LUO Zhong,YAN Yulong,HAN Qingkai,et al.Analysis of dynamic similarity of the rotor-bearing system and its effects of bearing parameters[J].Journal of Vibration and Shock,2012,31(S.):12-16.（in Chinese）

[10] Келъэон A C, Журавлев IO H, Январев Н В. РАСЧЕТ И КОНСТРОВАНИЕ РОТОРНЫХ МАШИН [M]. Ленинград《Машиностроение》,Пенинградское огдепение,1977:212-214.

[11]韩清凯.故障转子系统的非线性振动分析与诊断方法[M].科学出版社,2010:40-42.HAN Qingkai.Nonlinear vibration analysis and diagnosis methods of fault rotor system[M].Science Press,2010：40-42.（in Chinese）

[12]Chen Y D,Du R,Qu L S.Fault features of large rotating machinery and diagnosis using sensor fusion[J].Journal of Sound and Vibration,1995,188(2):227-242.

[13]路长厚,栾芝芸.砂轮不平衡量最小二乘识别研究[J].机械工程学报,1998,34(1):88-92.LU Changhou,LUAN Zhiyun,Study on identification of unbalance value of grinding wheels using a least-square method[J].Journal of Mechanical Engineering,1998,34(1):88-92.（in Chinese）

[14]Jalan A K,Mohanty A R.Model based fault diagnosis of a rotor-bearing system for misalignment and unbalance under steady-state condition[J].Journal of Sound and Vibration,2009,327(S3-S5):604-622.

[15]侯海云,李业农.不同轴承联合作用下转子系统的不平衡响应[J].南通职业大学学报,2010,24(1):90-94.HOU Haiyun,LI Yenong.The research on unbalance response of misalignment rotor-bearing system under both rolling and sliding bearings[J].Journal of Nantong Vocationa l College,2010,24(1):90-94.（in Chinese）

Reproduction Method for Unbalanced Faults of Rotor System

YE Rui-duo1，WANG Li-ping1，LUO Zhong1，WANG De-you2， LIU Yong-quan2
（1.School of Mechanical Engineeringamp;Automation，Northeastern University,Shenyang 110819,China；2.AECC Shenyang Engine Research Institute,Shenyang,110015,China）

Aiming at the problem of unbalanced feature reproduction of rotor system,a method of model reconstruction based on dynamic similarity criteria was presented.According to the vibration differential equation of the rotor system,the similarity relationship among rotor shaft,disk,flexible support and unbalance amount was established by the integral simulation method and dimensional analysis method.In the light of the similarity relationship,the dynamic similarity model of the prototype unbalanced rotor system was designed and the correctness was verified using finite element method.The least square method was used to identify the unbalance of the prototype and model rotor test bench system.The process of reproducing the unbalanced features was given.The effectiveness of the unbalanced feature reproduction design method was verified by experiment.Unbalanced feature reproduction method of rotor system was summarized based on dynamics similarity relationship.

rotor system;unbalance;dynamics similarity;fault reproduction;model test；large rotating machineries

V 231.96

A

10.13477/j.cnki.aeroengine.2017.03.007

2016-10-19 基金项目：国家自然科学基金(11572082)、教育部基本科研业务费专项资金 (N150304004,N140301001)、辽宁省高等学校优秀人才支持计划(LJQ2015038)资助

叶瑞夺（1991），男，在读硕士研究生，研究方向为转子系统模型试验技术与方法；E-mail：704172111@qq.com。

叶瑞夺，王丽萍，罗忠，等.转子系统不平衡故障的再现方法浅析[J].航空发动机，2017,43（3）：32-37.YE Ruiduo，WANG Liping，LUO Zhong，et al.Reproduction method for unbalanced faults ofrotor system[J].Aeroengine，2017,43（3）：32-37.

（编辑：栗枢）