光栅衍射光强分布的几种简易计算方法
曹卫军 如克亚木·哈力克
(1.昌吉学院初等教育学院 新疆 昌吉 831100;2.昌吉学院物理系 新疆 昌吉 831100)
光栅衍射光强分布的几种简易计算方法
曹卫军1如克亚木·哈力克2
(1.昌吉学院初等教育学院 新疆 昌吉 831100;2.昌吉学院物理系 新疆 昌吉 831100)
光栅衍射光强分布公式严格的数学推导涉及比较复杂的数学物理知识。而用半波带法、振幅矢量法、三角函数法计算并分析光栅衍射光强分布,计算过程简捷,物理图像清晰,便于学习者更好地理解光栅衍射光强分布规律。
光栅衍射;光强分布;计算方法
对于光的衍射现象的解释在光学发展历史中有特别重要的地位。在大学物理教材与物理教学中,光栅衍射光强分布公式一般不会给出严格的数学推导,因为涉及到比较复杂的数学物理知识。即便给出数学表达式,也因为复杂的推导,学生理解起来觉得很难。所以尝试用相对简易的方法来推导光栅衍射光强分布公式,并对光强分布特点进行分析。
1 光的衍射原理
1.1 光的衍射定义
光在传播过程中遇到尺寸比光波波长大得不多的障碍物或小孔时,它将偏离直线传播绕过障碍物进入其阴影区,形成光强不均匀分布的现象叫光的衍射。衍射时产生的明暗条纹或光环,叫衍射图样[1]。依据光源、衍射物、观察屏三者的距离,我们可以把衍射分为夫琅禾费衍射和菲涅耳衍射两种[2]。
1.2 光栅衍射原理
1.2.1 光栅的构成
广义的光栅指的是任何具有空间周期性的衍射屏。在平板玻璃上刻出系列的等宽度、等间距的平行刻痕,即为平面透射光栅。刻痕处不透光,相邻刻痕之间的光滑部分可以透光,等效于一个单缝。设定每个透光部分的宽度为a,不透光刻痕的宽度为b,光栅常数d=a+b。以下讨论光栅衍射规律时均指这种光栅,设光栅的总缝数为N,衍射角为θ。光栅衍射是单缝衍射和多缝干涉的综合效应,即光栅衍射原理会涉及到单缝衍射原理和多缝干涉原理。
1.2.2 单缝衍射
单缝衍射实验装置如图1所示。光源S置于凸透镜l1的左端焦平面,经l1折射以后的光束变为平行光,平行光垂直入射到单缝AB上[3]。根据惠更斯-菲涅耳原理,衍射光以θ衍射角经过透镜会聚于观察屏上P点时,其光强分布规律为:I=I0(sinu/u)2。
式中的I为单缝衍射在θ=0方向上的衍射光强,u=(πasinθ)/λ,a是单缝的宽度。
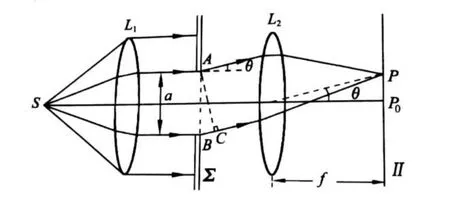
图1 单缝衍射示意图

图2 单缝干涉示意图
1.3 多缝干涉
干涉是频率相等、振动方向相同、具有恒定的相位差的两列或两列以上的波在空间叠加时发生光强重新分布的现象,多缝干涉如图2所示。多缝干涉的强度分布规律为
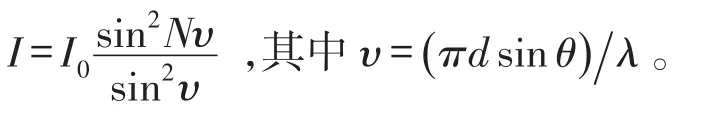
1.4 光栅衍射
光栅衍射示意图如图3所示,f为凸透镜焦距。依据惠更斯-菲涅尔原理,采用积分法可以计算出光栅衍射的光强表达式[4]为


图3 光栅衍射示意图
2 光栅衍射光强分布的计算与分析
2.1 半波带法计算
我们在用半波带法分析单缝衍射(如图4)的基础上,尝试用半波带法分析光栅衍射光强分布[5]。
2.1.1 光栅方程、主次大(明纹)
如果相邻两条缝发出的光波间的光程差刚好等于入射光波长的整倍数,那么N个缝的光束在光屏上P点处干涉加强,合振动振幅为最大值,则光强最大,在屏上呈现为明纹,叫主极大。即为光栅方程:

2.1.2 暗纹、次极大、缺级
如果光栅平面恰好分成偶数个半波带(如图5),每相邻两个半波带对应点之间的光程差,相位差为π,符合干涉相消的条件,光强为零,在光屏上形成暗纹。于是得到光栅衍射暗纹条件为:

式中,κ'≠0、N、2N...这属于光栅公式的衍射明纹情形。
从(2)式可以看出两个相邻的主极大之间有N-1条暗纹(极小),然而两个暗纹之间必然不能是暗纹,有一定光强,叫做次极大,可以推算出来,N-1条暗纹之间就会有N-2个次极大。即两个相邻的主极大之间存在N-1个极小,N-2个次极大。

图4 单缝衍射半波带
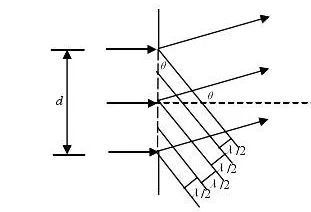
图5 光栅衍射半波带
2.2 三角函数法计算
2.2.1 计算
如图3所示,屏上某一点P处的电矢量是来各狭缝的电矢量的相干叠加。若P点对应的衍射角为θ,则相邻两狭缝间的光程差为δ=dsinθ。对于角频率为ω,波长为λ的单色光,设通过第一条狭缝的光在P点引起的振动为


于是,P点的合振动为

2.2.2 讨论
即dsinθ=kλ,k=0、±1、±2、±3...此式为光栅方程。

表明相邻两个主极大之间有N-1条极小。
③次极大。两个极小之间还存在光强较弱的次极大。相邻两个主极大之间存在N-1个极小,就必然会有N-2个次极大。
2.3 振幅矢量叠加法计算
2.3.1 计算
光栅中相邻两条光缝衍射出来的光线的光程差δ=dsinθ,相位差为总振幅Ap可用图6所示的矢量图解求出[8]。图中A1、A2、...AN-1、AN各矢量的长度都是每个单缝的合成振幅A,方向逐个相差Δφ的角度,所以折线OA1A2...AN是等边多边形的一部分,P是这个多边形的中心,等腰三角形POA1的顶角Δφ,于是
ΔPOQ是等腰三角形,顶角,所以合矢量Ap的长度为

图6 光栅衍射振幅矢量叠加

2.3.2 讨论
振幅矢量叠加法得到了三角函数法一样的光栅衍射光强公式。可以与2.2中一样讨论主极大、极小、次极大、缺级等条纹特征。然而,我们从振幅矢量叠加的特殊情况得到一些结论。
将每一单光束的振幅贡献看做一个分矢量,由于在同一θ下各分矢量的长度应该相等,只是相邻矢量产生了大小为Δφ的辐角变化,而这N个首尾相接的矢量总的转角则为,ΔφN=NΔφ。
显然,当θ=0时,Δφ=0,各分矢量取向相同(如图7(a)),合矢量为NA10,相应的光强为N2I10,这里的A10和I10分别表示单缝衍射时的中心点的的振幅和强度,而这一点称为零级主极大。
当δ=3λ/2N时,δN=3λ/2,ΔφN=3π矢量合成图转过一圈半(如图7(c)),合矢量取得极大值,称为一级次极大。
当δ=2λ/N时,δN=2λ,ΔφN=4π矢量合成图转过两圈(如图7(d)),由此可以得到了第二零点。
以下类推可以依次得到各高级次极大和零点。直到δ=λ时,Δφ=2π,各分矢量在后者比相邻前者多转过一圈的条件下又全部同向排列起来(如图7(e)),这时合成光强为表示在此衍射角θ1下单缝衍射的强度,相应位置θ1称为一级主极大。
θ在增加时,有重复零点和次极大交替出现的过程,直到δ=2λ时出现第二次主极大。然后零点和次极大又交替重复,直到δ=3λ时出现三级主极大[9]……。

图7 矢量图解法分析多缝衍射中的极点
3 几种计算方法的对比
综上所述,半波带法,振幅矢量法以及三角函数法来计算光栅衍射光强及分析条纹特点均比采取积分计算简单得多。振幅矢量法以及三角函数法可以得到与积分法一样的光栅衍射光强公式。
半波带法用比较粗糙的分割波面,虽然不够精细,但是可以很容易得出衍射图样的一些特征,常常被人们所喜用。三角函数法计算未涉及高深的数学知识,容易掌握,且逻辑关系清晰、物理意义明确,容易被学生接受。振幅矢量法既可以得到精确的光栅衍射光强公式,可与三角函数法计算得到结论一样讨论衍射图样特征,同时还可以从振幅矢量叠加的特殊情况下得到主极大、极小、次极大的特征。兼具前面两种计算方法的优点。
[1]姚启钧.光学教程[M].北京:高等教育出版社,2002:115-117.
[2]赵凯华,钟锡化.光学(下册)[M].北京:北京大学出版社,2004:2-11.
[3][4][9]蔡履中,王成彦,周玉芳.光学教程[M].济南:山东大学出版社,2002:222-223.
[5]吴颖,孙丽暖,徐恩生.半波带法在分析光栅衍射中的应用[J].辽宁工程技术大学学报.2005,(03).
[6]赵诗华,滕爱萍.光栅衍射的初步分析[J].大学物理,2005,(04).
[7]孙红辉,王红霞,许佳婷.光栅衍射中明暗条纹的分析讨论[J].课程教学研究,2016,(35).
[8]吴颖,徐恩生,罗宏超.振幅矢量法与半波带法分析光栅衍射的比较[J].沈阳航空工业学院学报,2005,(22).
O436.1
A
1671-6469(2017)-06-0103-05
2017-10-01
曹卫军(1969-),男,湖南双峰人,昌吉学院初等教育学院副教授,研究方向:物理教育、强激光场与物质相互作用。

