两类“磁聚焦”与“磁发散”问题探析

浙江 李军豪

平行微粒变会聚，发散微粒变平行。

两类“磁聚焦”与“磁发散”问题探析

所谓磁聚焦，是指利用特殊边界的匀强磁场，让从不同空间位置以相同速度、平行射入磁场的带电微粒束会聚于同一点的现象。所谓磁发散，是指从某一空间位置点沿不同方向、发射速率相同的带电微粒束，经磁场偏转后变为相互平行、同向运动的现象。

磁聚焦与磁发散，是两个相反的物理过程，具有情景新颖、能力要求高、思维难度大的特点，是磁场类高考命题的热点，能有效考查分析综合能力、逻辑推理能力、应用数学知识解决物理问题的能力。现选取两类经典案例，分类探究其发生的条件、遵循的规律及其拓展应用，供教学复习参考。

一、圆形磁场的聚焦与发散

圆形磁场的聚焦与发散是借助圆形边界的匀强磁场，使速度相同、相互平行的带电微粒聚焦于一点，和由某一固定点沿不同方向、发射速率相同的带电微粒，经磁场偏转后发散为相互平行的带电微粒的现象。画出规范的运动轨迹图，应用物理作图方法与数学方程方法，选取端值点与任意位置点的微粒来探究其规律，是求解这类问题的最有效途径。

【例1】如图1所示，x轴正方向水平向右，y轴正方向竖直向上。在xOy平面内有一个半径为R、与xOy平面垂直的匀强磁场。在圆形磁场的左边放置一带电微粒发射装置，它沿x轴正方向发射出一束具有相同质量m、电荷量q(qgt;0)和初速度v的带电微粒。发射时，这束带电微粒分布在0lt;ylt;2R的区间内。不计微粒重力，忽略微粒间的相互作用。

图1

(1)从A点射出的带电微粒平行于x轴从C点进入有磁场区域，并从坐标原点O沿y轴负方向离开，求磁感应强度的大小与方向。

(2)请指出这束带电微粒与x轴相交的区域，并说明理由。

(3)若这束带电微粒初速度变为2v，那么它们与x轴相交的区域又在哪里？并说明理由。

图2

图3

(2)这束带电微粒都通过坐标原点O。亦即这束带电微粒都将会聚于坐标原点O。理由及解法说明如下：

从任一点P水平进入圆形磁场的带电微粒，在磁场中做半径为R的匀速圆周运动，如图3所示。其中四边形PQOO′为菱形，边长为R，设P点与O′点的连线与y轴的夹角为θ，则∠QOO′=θ，微粒圆周运动的圆心Q的坐标为(-Rsinθ，Rcosθ)，故微粒圆周运动的轨迹方程为：(x+Rsinθ)2+(y-Rcosθ)2=R2①

又圆形磁场的圆心坐标为(0，R)，故圆形磁场的边界方程为：

x2+(y-R)2=R2②

联解①②两式，可得带电微粒做圆周运动的轨迹与磁场边界的两个交点坐标为：

x1=0、y1=0与x2=-Rsinθ、y2=R(1+cosθ)，

显然，后者坐标点(x2，y2)就是P点，须舍去。

可见，这束带电微粒都是通过坐标原点离开磁场的。

(3)这束带电微粒与x轴相交的区域是0lt;xlt;∞。理由说明如下：

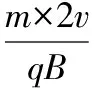
图4

很显然，靠近M点发射出的带电微粒穿过磁场后会射向靠近x轴正方向的无穷远处；靠近N点发射出的带电微粒穿过磁场后会射向靠近原点O处。

综上可知，这束带电微粒与x轴相交的区域范围是0lt;xlt;∞。

【规律小结】

综上可知，平行同方向运动的带电微粒在圆形磁场区域的聚焦问题，具有以下特点与规律：

(1)条件性。重力不计的带电微粒，在匀强磁场中做匀速圆周运动的半径r=mv/qB，与圆形磁场的半径R相同的条件下，才能使平行射入圆形磁场的带电微粒束会聚于一点。

(2)聚焦性。沿+x方向平行射入图1的圆形磁场的带正电微粒束，将会聚于磁场圆周的最低点；如果微粒束带负电，或者磁场方向相反，微粒束将会聚于磁场圆周的最高点。

(3)发散性。在图1中ygt;0的空间区域，从坐标原点O处沿不同方向射出的速率相同的带正电的微粒束，经圆形磁场偏转后都将沿+x方向平行射出；如果微粒束带负电，或磁场方向相反，经圆形磁场偏转后都将沿-x方向平行射出。

(4)可逆性。聚焦与发散是两个相反、可逆的过程，运用圆形磁场的组合，或者改变微粒束的电性，或者改变磁场方向，可以实现磁聚焦与磁发散的逆向转换。

明确圆形磁场的聚集与发散的条件，以及会聚性、发散性、逆向性的规律，就能快速、有效地求解更深层次的同类问题。

【拓展应用】

【例2】真空中有一半径为r的圆柱形匀强磁场区域，磁场方向垂直于纸面向里，Ox为过边界上O点的切线，如图5所示，从O点在纸面内向各个方向发射速率均为v0的电子，设电子间相互作用忽略，且电子在磁场中偏转半径也为r。已知电子的电量为e，质量为m。

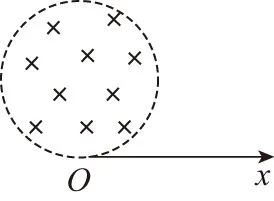
图5

图6

(1)速度方向分别与Ox方向夹角成60°和90°的电子，在磁场中的运动时间分别为多少；

(2)所有从磁场边界出射的电子，速度方向有何特征；

(3)今在某一平面内有M、N两点，其水平间距MN=l，从M点向平面内各个方向发射速率均为v0的电子。请在图6中设计一种匀强磁场分布，使得由M点发出的电子都能够汇聚到N点，并求出匀强磁场的磁感应强度B的最小值。

【解析】(1)如图7所示，令入射时电子速度与x轴夹角为θ，其入射点为O，射出点为A。由于电子在磁场中偏转半径与圆形磁场区域半径相等，故无论入射的速度方向与x轴的夹角为何值，磁场区域圆心O1和电子圆周运动轨道圆心O2一定组成边长为r的菱形。

图7

因O1O⊥Ox，OO2垂直于入射速度，故∠OO2A=θ。即电子在磁场中所转过的角度一定等于入射时电子速度与Ox轴的夹角。

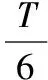
(2)因O2A∥OO1，且O1O⊥Ox，故O2A⊥Ox。又O2A与电子射出的速度vA方向垂直，可知电子射出方向vA一定与Ox轴方向平行，即vA⊥Ox，故所有的电子射出圆形磁场时，速度方向均与Ox轴同方向、且相互平行。

(3)由于磁发散与磁聚焦的路径是可逆的，所以从图7中的圆形磁场射出的这些速度相同、相互平行的电子束，若再进入一相同的圆形匀强磁场后，一定会聚焦于某一点。

在图8所示中，四个圆形磁场的半径相同，磁感应强度大小相等，磁场方向上下相反，上下圆形磁场分别与MN相切，其中，M、N为切点。

图8

对于从M点向MN连线上方射出的电子，经圆形磁场MM1与NN1依次发散、磁聚后，都能够汇聚到N点。同理，对于从M点向MN连线下方射出的电子，经圆形磁场MM2与NN2依次发散、磁聚后，亦都能够会聚到N点。

【特别说明】例2中的磁场设计，涵盖圆形磁场的发散与聚焦两个过程。图8中的磁场分布，只是符合题意的磁场之一，是符合题意的磁场面积最小的情形。其实，只要在矩形区域M1N1M2N2内除图中四个半圆形磁场外必须无其他磁场存在，矩形M1N1M2N2区域外的磁场均可向其余区域扩展。

二、“叶形”磁场的聚焦与发散

什么形状的匀强磁场，使磁场区域的面积最小，也能使速度相同、相互平行的带电微粒聚焦于一点，或者由某一固定点沿不同方向发射的速率相同的带电微粒，经过磁场偏转后发散为相互平行的带电微粒？要探究这类问题的规律性，关键是要建立起正确的空间几何图形，具备扎实的数学知识，特别是圆的方程知识。这类问题重在考查探究性、创造性的思维能力，以及深层次应用数学知识解决物理问题的能力。

【例3】如图9所示，ABCD是边长为a的正方形。质量为m、电荷量为e的电子以大小为v0的初速度沿纸面垂直于BC边射入正方形区域。在正方形内适当区域中有匀强磁场。电子从BC边上的任意点入射，都只能从A点射出磁场。不计重力，求：

图9

(1)此匀强磁场区域中磁感应强度的方向和大小；

(2)此匀强磁场区域的最小面积。

【解析】(1)如图9所示，设磁场的磁感应强度大小为B。现考察特殊情形，即电子自C点垂直于BC入射，其运动轨迹为圆弧CEA，圆弧的圆心在A、C连线的中垂线上，故B点即为圆周运动的圆心。由左手定则可知，磁场的方向应垂直于纸面向外。

由图10可知，电子做圆周运动的半径为r=a，

(2)由(1)中决定的磁感应强度B的方向和大小情形下，自C点垂直于BC入射的电子，在A点沿DA方向射出；自BC边上其他点垂直入射的电子，其运动轨迹只能在BAEC区域中。故圆弧CEA是所求的最小磁场区域的一个边界。

为了确定该磁场区域的另一边界，我们来考查自BC边上任意点垂直BC入射的电子的情形。设该电子的运动轨迹qpA如图10所示，其中，qp为无磁场区域做匀速直线运动，圆弧pA为磁场区域做匀速圆周运动，运动半径r仍然为a。

图10

若以A为坐标原点，以AB为x轴、AD为y轴，建立直角坐标系，并设从A点射出的电子的速度方向与x轴负方向的交角为θ，则磁场边界入射点P的坐标(x,y)数值为：

x=asinθ，y=a-acosθ，

显然，其满足以下圆方程：x2+(y-a)2=a2。

这意味着，电子射入磁场的点p，是以D为圆心、a为半径的四分之一圆弧CFA，即圆弧CFA是电子做直线运动与圆周运动的分界线，也就是构成所求最小磁场区域的另一边界。

因此，所求的最小匀强磁场区域，就是分别以B和D为圆心，以a为半径的两个四分之一圆弧CEA和CFA所围成的区域，其最小面积数值为：

【规律小结】综上可知，平行同方向运动的带电微粒在最小磁场区域的聚焦问题，具有以下特点与规律：

(1)条件性。最小磁场区域的两个边界，就是两个正对的半径相同的四分之一圆周的圆弧；最小的磁场面积就是两个四分之一圆弧之交集的面积。最小磁场区域形状呈“叶形”。

(2)聚焦性。沿-x方向平行射入图10“叶形”磁场的电子束，将会聚于“叶形”磁场的最低点(A点)；若电子束沿+x方向平行射入“叶形”磁场，将会聚于“叶形”磁场的最高点(C点)。

(3)发散性。若改变图10中的磁场方向，则从坐标原点A向第Ⅰ象限射入速率相同、方向不同的电子束，经“叶形”最小磁场偏转后发散，将变为平行于+x轴方向的电子束离开。

若从图10磁场的最高点C向“叶形”磁场内射入速率相同、方向不同的带正电粒子束，经磁场偏转后发散，将变为平行于-x轴方向的粒子束离开。

(4)可逆性。运用“叶形”磁场的组合与对接，或者改变微粒束的电性，或者改变磁场的方向，可以实现磁聚焦与磁发散的逆向转换。

浙江省衢州第一中学)