基于MATLAB和学科竞赛构建高等数学研究性教学课堂
曹玉松+邱颖豫+鄢靖丰

摘 要:文章分析了MATLAB和学科竞赛的特点。以研究性教学为目标,以学科竞赛为依托,将MATLAB和学科竞赛引入到高等数学课堂,从而构建高等数学的研究性教学课堂,为高等数学的研究性教学提供了参考建议。
關键词:学科竞赛;研究教学;教学改革;高等数学
一、 概述
高等数学是理工科各专业的基础课,它所提供的数学思想、数学方法是理工科各专业学生学习其后续课程的基础,但是传统的教学方法重理论,轻应用,使得学生对高等数学的应用能力不强,从而不能很好地为专业课服务,为学科竞赛服务。高等数学自身具有理论严谨抽象,内容繁杂的特点,传统的教学模式重理论,轻应用,使得学生对涉及的部分理论知识没有一个直观的认识,相应地会产生危难情绪,久而久之学习兴趣下降,因此有必要对现有的高等数学教学模式进行改革。
MATLAB具有强大的数值计算功能,可以方便地处理矩阵计算,进行图形绘制,符号运算,程序设计,仿真应用,将MATLAB引入到高等数学教学中,可以有效地激发学生的学习兴趣和动手能力,是一种具有实践意义的教学方法。
近年来,学科竞赛在各大高校开展得轰轰烈烈,学科竞赛是培养大学生创新实践能力和动手能力的重要途径,通过学科竞赛可以锻炼学生的动手能力,学生的团队合作意识,学科竞赛的重要载体就是研究性教学模式的构建。
基于MATLAB 和学科竞赛的以上特点,我们可以把学科竞赛和MATLAB引入高等数学课堂教学中,构建高等数学的研究性课堂,把传统的仅靠板书的课堂改为与计算机相结合,提高学生学习高等数学的兴趣,本文从下面几个方面说明如何将MATLAB和学科竞赛相关内容引入到高等数学课堂构建研究性教学模式。
二、 将MATLAB引入到高等数学课堂构建研究性课堂案例
理工科的学科竞赛会大量应用到高等数学的相关知识,各类模型的构建都离不开高等数学知识,若直接利用高等数学解决相关问题会带来许多不便,MATLAB提供的数值运算、图像绘制、程序设计和系统仿真等功能,可以利用简单的命令函数命令实现,可以将使用者从繁琐的运算中解放出来,方便快捷地实现相关问题的求解。
(一) 利用MATLAB拟合曲线
根据输入数据X和Y生成一个N阶的拟合多项式。D=polyval(p,x),根据数据X,用拟合多项式p生成拟合好的数据。
案例1:下面这组数据为检测仪器采样结果:2,7,12,17,22,17,32,37,42,47,52,57,求这组数据的拟合方程。
方法:在MATLAB命令提示符下输入:
>> clear
>> d=1:12;
>> a=[2 7 12 17 22 17 32 37 42 47 52 57];
>> p=polyfit(d,a,4);
>> px=poly2str(p,x');
>> pv=polyval(p,d);
>> p,pv
p=-0.0102 0.2561 -2.0158 10.1771 -6.5354
pv=
Columns 1 through 6
1. 8718 7.6410 11.9417 15.6985 19.5913 24.0552
Columns 7 through 12
29.2805 35.2129 41.5532 47.7576 53.0373 56.3590
>> plot(d,a,d,pv)
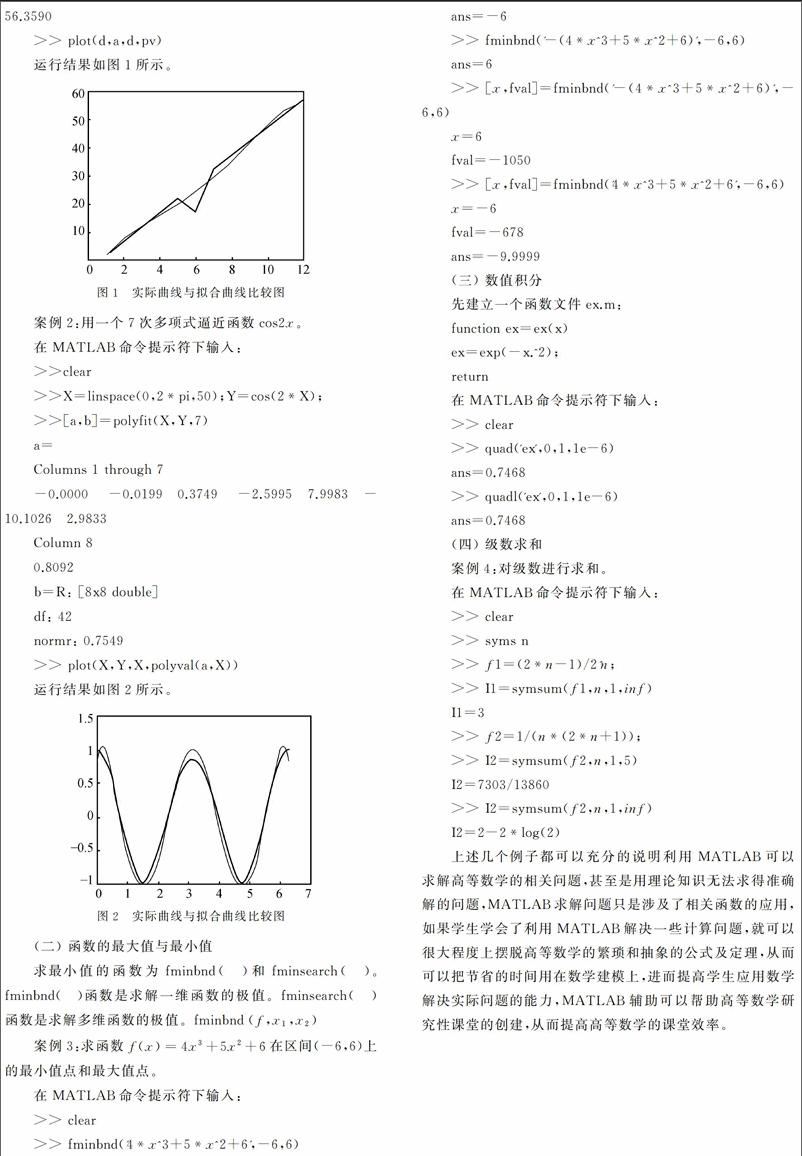
运行结果如图1所示。
案例2:用一个7次多项式逼近函数cos2x。
在MATLAB命令提示符下输入:
>>clear
>>X=linspace(0,2*pi,50);Y=cos(2*X);
>>[a,b]=polyfit(X,Y,7)
a=
Columns 1 through 7
-0.0000 -0.0199 0.3749 -2.5995 7.9983 -10.1026 2.9833
Column 8
0.8092
b=R:[8x8 double]
df:42
normr:0.7549
>> plot(X,Y,X,polyval(a,X))
运行结果如图2所示。
(二) 函数的最大值与最小值
求最小值的函数为fminbnd( )和fminsearch( )。fminbnd( )函数是求解一维函数的极值。fminsearch( )函数是求解多维函数的极值。fminbnd(f,x1,x2)
案例3:求函数f(x)=4x3+5x2+6在区间(-6,6)上的最小值点和最大值点。
在MATLAB命令提示符下输入:
>> clear
>> fminbnd('4*x^3+5*x^2+6',-6,6)
ans=-6
>> fminbnd('-(4*x^3+5*x^2+6)',-6,6)
ans=6
>> [x,fval]=fminbnd('-(4*x^3+5*x^2+6)',-6,6)
x=6
fval=-1050
>> [x,fval]=fminbnd('4*x^3+5*x^2+6',-6,6)
x=-6
fval=-678
ans=-9.9999endprint
(三) 数值积分
先建立一个函数文件ex.m:
function ex=ex(x)
ex=exp(-x.^2);
return
在MATLAB命令提示符下輸入:
>> clear
>> quad('ex',0,1,1e-6)
ans=0.7468
>> quadl('ex',0,1,1e-6)
ans=0.7468
(四) 级数求和
案例4:对级数进行求和。
在MATLAB命令提示符下输入:
>> clear
>> syms n
>> f1=(2*n-1)/2^n;
>> I1=symsum(f1,n,1,inf)
I1=3
>> f2=1/(n*(2*n+1));
>> I2=symsum(f2,n,1,5)
I2=7303/13860
>> I2=symsum(f2,n,1,inf)
I2=2-2*log(2)
上述几个例子都可以充分的说明利用MATLAB可以求解高等数学的相关问题,甚至是用理论知识无法求得准确解的问题,MATLAB求解问题只是涉及了相关函数的应用,如果学生学会了利用MATLAB解决一些计算问题,就可以很大程度上摆脱高等数学的繁琐和抽象的公式及定理,从而可以把节省的时间用在数学建模上,进而提高学生应用数学解决实际问题的能力,MATLAB辅助可以帮助高等数学研究性课堂的创建,从而提高高等数学的课堂效率。
三、 将MATLAB引入到学科竞赛
学科竞赛是在课堂教学的基础之上,考查学生利用所学的基础知识和专业知识解决实际问题的能力。当前,越来越多的学校都花费了大量的人力物力投入到学科竞赛中,学科竞赛对学习的促进效果已经显现出来,开展学科竞赛可以培养学生的动手能力和团队协作能力,提高理工科学生的工程能力,学科竞赛的成绩已成为衡量教学水平和教学质量的重要指标。但在学科竞赛中常常会面临一些无法用理论求得精确解的问题,但是MATLAB提供的强大的计算功能却可以给出其数值解,从而解决学科竞赛中的实际问题,另外,即使对于一些可以用理论知识求解的问题,利用MATLAB也可以大大地节约运算时间,因此MATLAB引入到学科竞赛解决相应的数学模型具有较强的现实意义,这就要求在高等数学课堂上需要将MATLAB和学科竞赛相结合,利用案例教学,构建高等数学的研究性教学课堂。
四、 结束语
基于MATLAB和学科竞赛构建高等数学研究性教学课堂,旨在将MATLAB和学科竞赛中的部分案例教学引入到高等数学课堂教学中去,MATLAB强大的数值计算功能大大增加了高等数学的实用性,弱化了高等数学的抽象程度,学科竞赛案例的引入可以使得高等数学与专业问题结合起来,提高学生分析问题、解决问题的能力。
参考文献:
[1] 林海涛.MATLAB在《高等数学》教学中的辅助功效研究 [J].开封教育学院学报,2016,36(5):133-134.
[2] 李小梅,叶赛英.重探究、重应用、重体验——研究性学习法的具体举例——以高等数学课程为例.数学教学研究,2014,33(2):45-49.
[3] 徐永梅.高等数学实施探究性教学模式教学效果评价模型分析.价值工程,2016, 35(16):188-190.
[4] 陈莹,肖依,赵中.高等数学研究性学习教学法.洛阳师范学院学报,2015(2):124-126.
[5] 汤永龙,黄锦,唐云华.高等数学教学改革之研究.课程教育研究,2014(30):54-55.
[6] 曹玉松,邱颖豫.基于学科竞赛的高等数学研究性教学的构建.吉林省教育学院学报,2016,32(6):75-77.endprint

