分布式流言push-sum无梯度算法
李德权,王孝梅,马 驰
(安徽理工大学数学与大数据学院,安徽 淮南,232001)
分布式流言push-sum无梯度算法
李德权,王孝梅,马 驰
(安徽理工大学数学与大数据学院,安徽 淮南,232001)
研究多个体网络中所有个体目标函数之和最小值问题,其中每个个体仅知其自身目标函数且仅可与其邻居个体交互信息。鉴于个体目标函数通常非光滑,同时个体间单变量信息通信有一定局限性,本文提出一种分布式流言push-sum无梯度算法求解此优化问题。假设每个个体都具有一个服从泊松分布的控制时钟,时钟的每次转动表示随机选择的个体之间进行信息更新。进一步地,在网络连通条件下证明了所提算法的收敛性。数值仿真结果表明,与现有的分布式流言无梯度优化算法相比,本文算法具有更快的收敛速度。
多个体网络;网络优化;分布式优化;流言算法;push-sum算法;无梯度算法
近年来多个体网络分布式优化算法已成为研究热点。众多应用领域问题都可转化为多个体网络中的分布式优化问题,如:分布式控制、分布式信号处理、大规模机器学习和无线网络分布式估计等。分布式优化的目的是通过个体间局部交互信息求解关于整个网络目标函数的最小值,目前解决此类问题的一种经典方法是流言算法。例如,Iutzeler等[1]针对无线传感器网络,结合权重结构和广播流言的特性,深入分析了Sum-Weight-like算法中初始值均值的收敛性,认为其平方误差随时间呈指数级下降;Khosravi等[2]基于流言算法求解传感器网络中强连通拓扑结构下初始状态的确切平均值,数值仿真结果表明,该算法在传输次数、收敛速度和精度等方面具有优势;Lu等[3]使用Pairwise Equalizing和Pairwise Bisectioning两种流言算法求解时变无向网络拓扑结构下无约束的、可分的、一致凸性的优化问题,其中每个个体函数是严格凸性的、连续可微的且有一个极小值;Aysal等[4]探讨用于单变量信息通信的广播流言算法,并证明了该算法的收敛性。需要指出的是,文献[1-4]的研究主要基于个体间利用单变量信息通信达成一致,但单变量信息通信仅在有向平衡网络中才能确保所有个体状态达成平均一致性。实际应用中,由于个体自身储存能量有限或感知能力的不同,导致网络往往是时变、非平衡的,故有向平衡网络的条件难以保证。为了克服这一不足,Franceschelli等[5]提出利用双变量信息通信,即push-sum机制确保所有个体达成平均一致性,其中一个变量表示个体状态估计的平均值,另一个变量表示个体的加权平均值,且每次迭代交互的信息是两个变量的比值。张晓倩[6]提出了多个体系统分布式push-sum次梯度优化算法,该算法中个体间同步进行信息交流,即所有个体同时进行更新迭代,因此个体间需要相互等待。
目前分布式优化多是在网络中个体目标函数次梯度存在或易于计算这一关键假设下进行研究的,但实际中存在大量个体目标函数次梯度难以计算的情况[7-8]。无梯度算法采用高斯近似函数代替原来的目标函数,可有效避免目标函数次梯度的计算,因而适用范围更广。
本文基于随机流言算法[9]和无梯度算法[7],并结合push-sum机制提出分布式流言push-sum无梯度(distributed gossip-based push-sum gradient-free,DGPSGF)算法来求解多个体网络优化问题,并对该算法在递减步长下的收敛性进行证明,最后通过数值仿真验证该算法的有效性。
1 符号说明
多个体网络信息通信通常建模成有向图G(k)=(V,E(k)),其中,V={1,2,…,n}表示网络中个体的集合,E(k)={(i,j)|i,j∈V}表示个体间的有向边集。N(i)表示个体i的邻居集合,即N(i)={j∈V;{i,j}∈E(k)}。s(k)=[s1(k),s2(k),…,sn(k)]T表示个体在k时刻的状态,‖s‖表示向量s的范数,E(s)表示向量期望,f(s)表示函数f(s)在s处的梯度。
2 问题描述
本文考虑由n个个体构成的多个体网络,目的是个体间相互合作解决以下分布式优化问题:
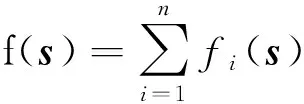
(1)
其中fi(s):Rm→R表示个体i的目标函数,每个个体仅知其自身的目标函数。
设最优解集为S*,当所有个体状态s1=s2=…=sn=s*∈S*时,则所有个体状态达成一致,且f(s*)为优化问题(1)的最优解。由于fi(s)的次梯度难以计算或不存在,为此本文采用一种无需计算每个个体目标函数次梯度的方法来求解网络优化问题。
3 算法介绍
3.1 异步时间网络模型
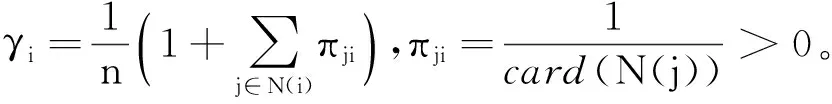
3.2 假设条件
假设1Fk+1表示算法迭代到Zk时刻的一个σ域,即Fk+1={xi(0);i∈V}∪{Il,Jl;0≤l≤k+1}
假设2G(k)=(V,E(k))是连通图,个体i随机选择邻居的过程是独立同分布的且选择的概率为πji>0(当j∉N(i)时,πji=0)。
3.3分布式流言push-sum无梯度算法
DGPSGF算法依据以下规则进行迭代更新:
当k>0、i∉{Ik,Jk}时,xi(k)=xi(k-1);否则,
si(k)=zi(k)/wi(k)
xi(k)=zi(k)-ηi(k)Gi(k)
式中:xi(k)是个体i在k时刻的状态值;ηi(k)是逐渐递减的迭代步长;随机无梯度预测值Gi(k)可表示为[10]
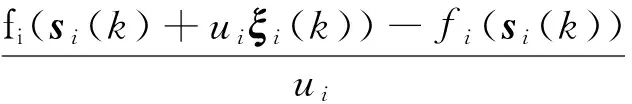
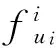
为便于分析,给出DGPSGF算法的另一个形式。首先定义非负矩阵A(k)=[aij(k)]∈Rn×n(aij(k)≥0)如下:
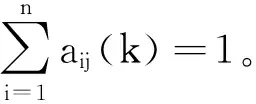
(2)
(3)
si(k)=zi(k)/wi(k)
(4)
xi(k)=zi(k)-ηi(k)Gi(k)i∈{Ik,Jk}
(5)
引理1[7]令G0(fi)是fi(s)的Lipschitz常数,对每一个i∈V有以下结论成立:
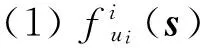
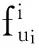
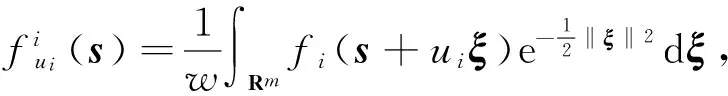
E[Gi(k)|Fk+1]=
(3) 随机无梯度预测值Gi(k)满足
4 收敛性分析
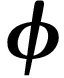
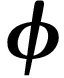
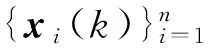
设s*∈Rn是任意向量,则有

(6)
参照文献[11]可得:
(7)
将式(7)代入式(6)整理得:
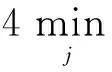
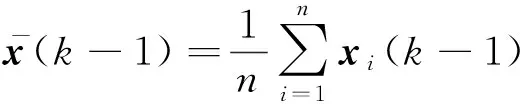
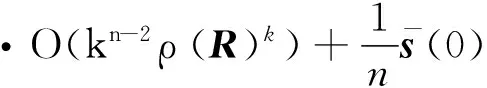
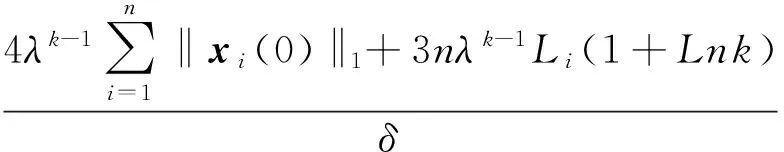
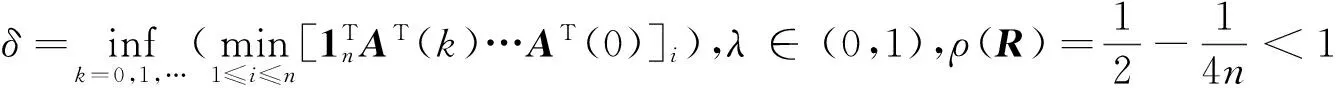
证明:参照文献[1]推得
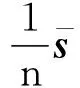
(8)
此外,参照文献[12]可得
(9)

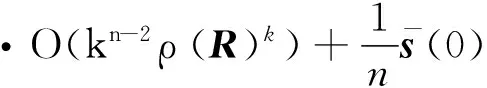
证毕。
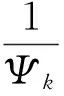

(10)
其中ηmax是个体i的最大步长。
证明:由引理3和引理4得
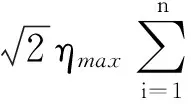
(11)
(12)
当ρ(R)<1且T→时,由式(12)可推得式(10)成立,证毕。
5 仿真实验分析
前面已理论上证明了DGPSGF算法求解优化问题(1)的收敛性。下面通过仿真实验来验证该算法的有效性,为此考虑一个具体的多个体优化问题[7]:
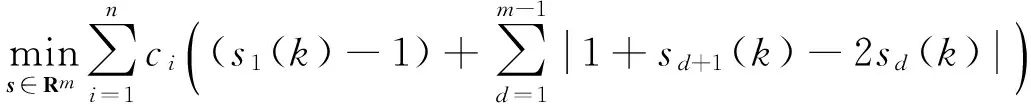
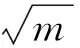
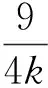

(a) (b) (c)
图1随机网络(n=3)
Fig.1Randomnetworkwiththreeagents
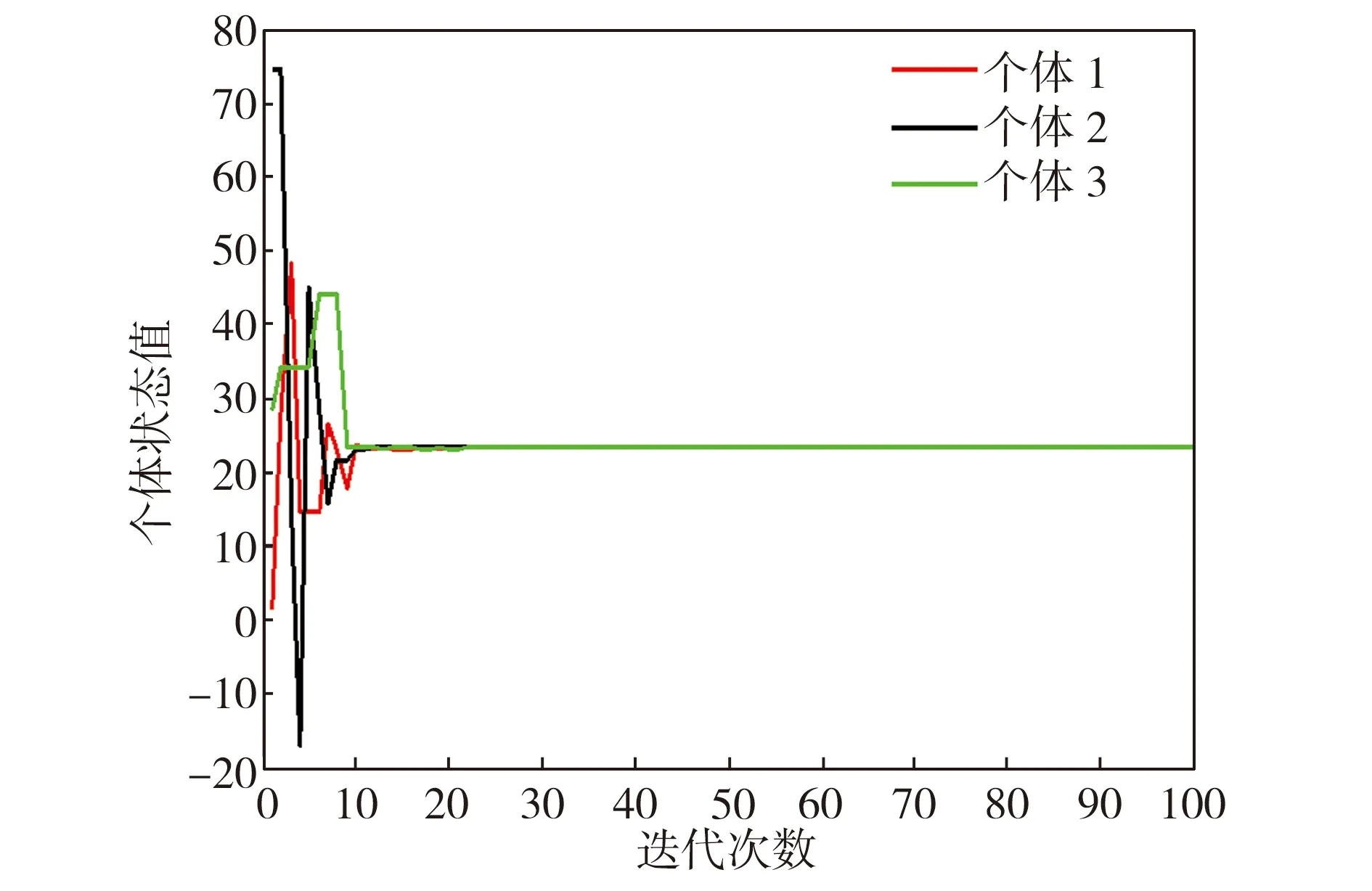
(a)u=3.5×10-6
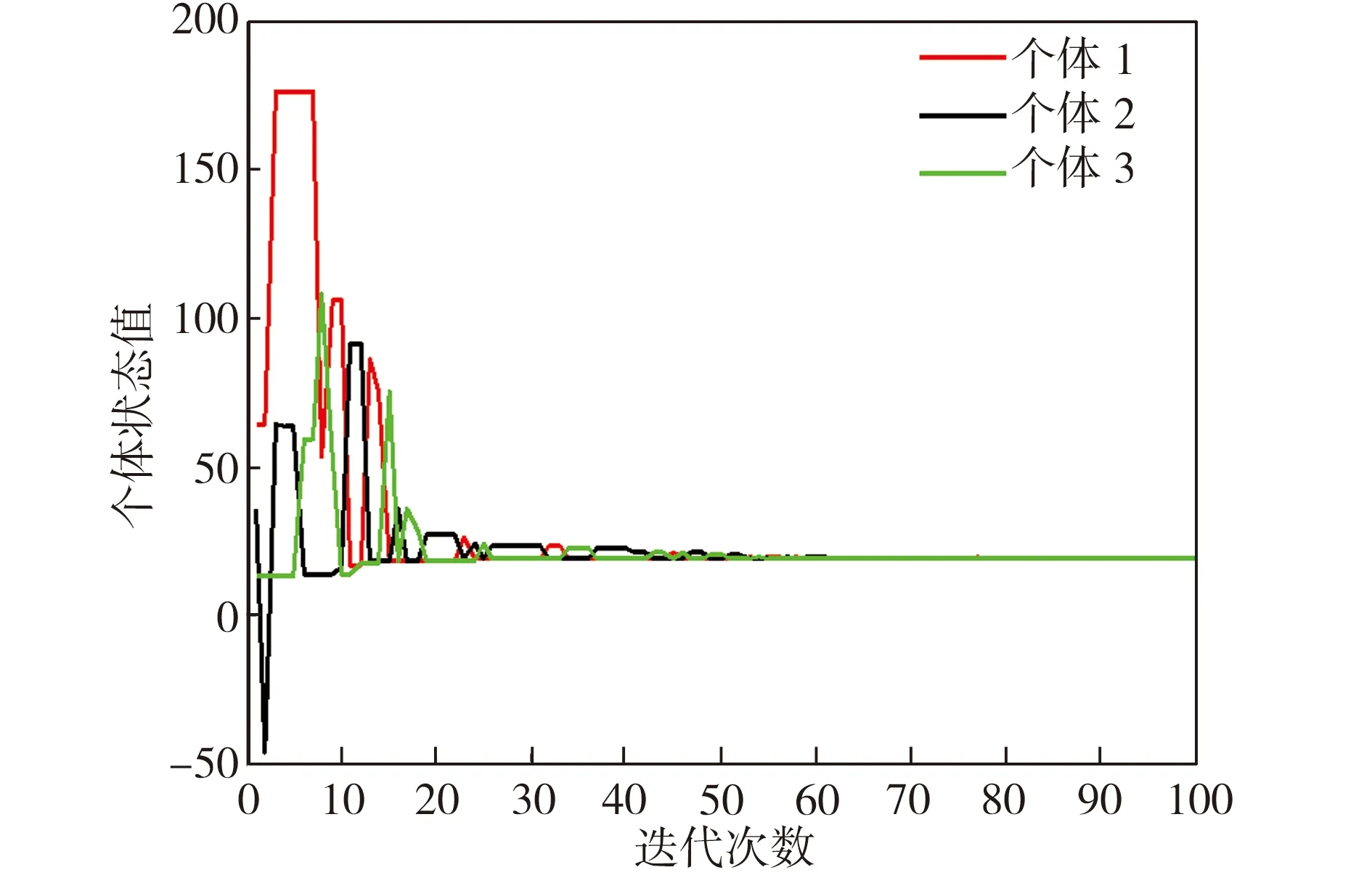
(b)u=3.5×100.5
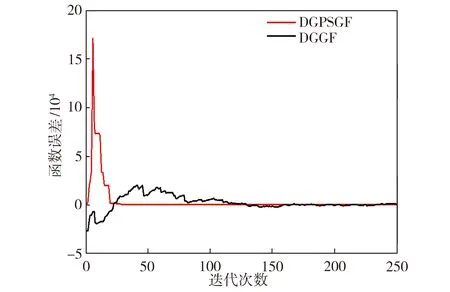
图3采用DGGF和DGPSGF算法的目标函数误差值对比
Fig.3ComparisonofobjectivefunctionerrorsbyDGGFandDGPSGFalgorithmsrespectively
6 结语
针对时变网络中个体目标函数具有非光滑性以及分布式单变量信息通信算法的局限性,本文提出分布式流言push-sum无梯度(DGPSGF)算法求解网络优化问题。假设每个个体都具有一个服从泊松分布的控制时钟,时钟的每次转动表示随机选择的个体之间进行信息更新,进而在网络连通的假设下,证明了该算法在递减步长下的收敛性。DGPSGF算法无需计算时变网络中个体目标函数的次梯度,且可有效克服单变量信息通信算法的局限性,因而更具实用性,并且与现有的分布式流言无梯度算法相比,本文算法具有更快的收敛速度。
[1] Iutzeler F, Ciblat P, Hachem W. Analysis of Sum-Weight-like algorithms for averaging in wireless sensor networks[J]. IEEE Transactions on Signal Processing, 2013,61(11):2802-2814.
[2] Khosravi A, Kavian Y S. Broadcast gossip ratio consensus: asynchronous distributed averaging in strongly connected networks[J]. IEEE Transactions on Signal Processing, 2017,65(1):119-129.
[3] Lu J, Tang C Y, Regier P R, et al. Gossip algorithms for convex consensus optimization over networks[J]. IEEE Transactions on Automatic Control, 2011,56(12):2917-2923.
[4] Aysal T C, Yildiz M E, Sarwate A D, et al. Broad-cast gossip algorithms for consensus[J]. IEEE Transactions on Signal Processing, 2009,57(7):2748-2761.
[5] Franceschelli M, Giua A, Seatzu C. Distributed averaging in sensor networks based on broadcast gossip algorithms[J]. IEEE Sensors Journal,2011,11(3):808-817.
[6] 张晓倩. 多个体系统分布式Push-sum次梯度优化算法的研究[D]. 淮南:安徽理工大学, 2015.
[7] Nesterov Y, Spokoiny V. Random gradient-free minimization of convex function[J]. Foundations of Computational Mathematics,2017,17(2):527-566.
[8] Com A R, Scheinberg K, Vicente L N. Introduction to derivative-free optimization, MPS-SIAM series on optimization[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2009.
[9] Boyd S, Ghosh A, Prabhakar B, et al. Randomized gossip algorithms[J]. IEEE Transactions on Information Theory,2006,52(6):2508-2530.
[10] Yuan Deming. Asynchronous gossip-based gradient-free method for multiagent optimization[J]. Abstract and Applied Analysis, 2014, Vol.2014: Article ID 618641.
[责任编辑尚晶]
Distributedgossip-basedpush-sumgradient-freealgorithm
LiDequan,WangXiaomei,MaChi
(School of Mathematics and Big Data, Anhui University of Science and Technology, Huainan 232001, China)
This paper studies how to collaboratively minimize the whole objective function of the multi-agent network, wherein each agent just knows its own objective function and only interacts with its neighboring agents. Because each agent’s local objective function is usually non-smooth and the method of single variable information communication among agents has some limitations, a distributed gossip-based push-sum gradient-free (DGPSGF) algorithm is proposed to solve this optimization problem. It is assumed that each agent has a local Poisson clock, and at each tick of its clock rotation, the agent interacts with randomly selected agents. Furthermore, the convergence of DGPSGF algorithm is proved under the mild assumption on the network connectivity. Numerical simulation results show that, compared with the existing distributed gossip-based gradient-free algorithm, the proposed DGPSGF algorithm has faster convergence rate.
multi-agent network; network optimization; distributed optimization; gossip algorithm; push-sum algorithm; gradient-free algorithm
TP13
A
1674-3644(2017)06-0472-06
2017-07-26
国家自然科学基金资助项目(61472003);高校学科(专业)拔尖人才学术资助重点项目(gxbjZD2016049);安徽省学术和技术带头人及后备人选科研活动经费资助项目(2016H076).
李德权(1973-),男,安徽理工大学教授,博士.E-mail:leedqcpp@126.com
10.3969/j.issn.1674-3644.2017.06.012

