沥青路面在半正弦荷载下的力学响应
吕悦晶,魏彩霞,应保胜,邹丽琼,周兴林,张沪生
(武汉科技大学汽车与交通工程学院,湖北 武汉,430081)
沥青路面在半正弦荷载下的力学响应
吕悦晶,魏彩霞,应保胜,邹丽琼,周兴林,张沪生
(武汉科技大学汽车与交通工程学院,湖北 武汉,430081)
研究轮胎/路面的接触印迹特征及随机荷载作用特点,采用ABAQUS软件构建路面结构三维有限元模型,对半正弦荷载作用下的沥青路面力学响应进行分析。结果表明,半正弦荷载作用下沥青路面的上面层和中面层出现应力应变集中,应力应变值随路面深度的增加而逐渐减小;沥青路面的竖向、横向及纵向应力最大值均出现在上面层,且竖向应力最大,横向应力次之,纵向应力最小;竖向、横向应变最大值出现在上面层,纵向应变最大值出现在上-中面层,且路面结构内部出现反复的纵向拉-压变形,这很可能是沥青路面轮迹带附近材料产生疲劳损坏的根本原因。另外,荷载作用时间和路面温度对沥青路面应变的影响要大于其对应力的影响,路面温度的升高导致应变增大且延迟了残余应变的恢复时间。
沥青路面;力学响应;半正弦荷载;有限元分析;轮胎/路面接触印迹;应力应变
《公路沥青路面设计规范》(JTG D50—2006)规定,沥青路面设计以双轮组单轴载100 kN为标准轴载(BZZ-100),路面结构设计采用静态垂直双圆均布荷载作用下的弹性层状体系理论进行计算,并以路表弯沉及面层和基层底部弯拉应力作为控制指标。该规范忽略了行驶过程中车辆荷载的动态性、随机性和非均匀分布性,并将接触印迹理想化,且仅以结构层应力指标作为设计控制标准。
然而,在行驶状态下车辆对路面除了施加垂直静态应力(σz)之外,还施加有纵向应力(σy)、横向应力(σx)和振动力;轮胎与路面接触印迹随荷载的变化而改变,并非理想圆形;路面各结构层材料也不具有理想弹性;路面响应除了应力之外,结构层应变特征亦不容忽视。因此,建立动荷载作用下的轮胎路面模型,分析轮胎路面接触应力分布、印迹变化,提出典型路面材料结构层力学响应特征的力学解释,这对研究路面结构的早期损坏规律及成因具有现实意义。
本文拟采用ABAQUS有限元数值分析软件,建立典型黏弹性层状沥青路面有限元模型,对半正弦荷载作用下的沥青路面力学响应进行探讨,以期为路面结构受力分析及早期病害诊断提供理论依据,并从力学角度出发为沥青路面材料设计提供新思路。
1 有限元模型的建立
沥青路面结构是三维空间层状构造体,所受荷载随时间和空间而变化。路面二维结构模型在进行荷载分析时只能施加轴对称荷载,不能同时分析路面三个方向的应力及应变情况,因此沥青路面有限元结构受力分析时最好采用三维模型。沥青路面面层材料是一种典型的黏弹性材料,对荷载应力和温度应力具有明显的依赖性。传统的沥青路面层状弹性结构理论并不能很好地描述沥青路面的真实受力状态[1-2],本文在沥青路面结构动力响应分析中引入黏弹性材料参数,模拟深度方向上材料的不均匀特性,并分析沥青路面结构受力特点。
1.1 路面结构及材料参数
以湖北省某高速公路典型沥青路面结构作为有限元分析对象,假设材料各层各向同性,构建三维黏弹性层状体系路面结构模型。路面结构及材料如图1所示,材料参数见表1。
沥青路面结构力学响应受温度、荷载及加载时间的影响。本文采用剪切模量的Prony级数序列来表征黏弹性材料对时间t的依赖性。沥青路面材料模型Prony级数基本形式为式(1),级数参
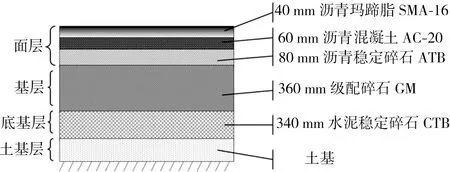
图1 沥青路面结构及材料
Fig.1Structureandmaterialsoftheasphaltpavement
数如表2所示。
(1)
式中:G(t)为剪切模量;t为蠕变时间;G0为初始剪切模量(t=0);τi为松弛时间;α∞、αi为相对模量;n为Prony级数的项数。

表1 沥青路面材料参数
表2沥青路面材料的Prony级数参数
Table2Pronyseriesparametersoftheasphaltpavementmaterials
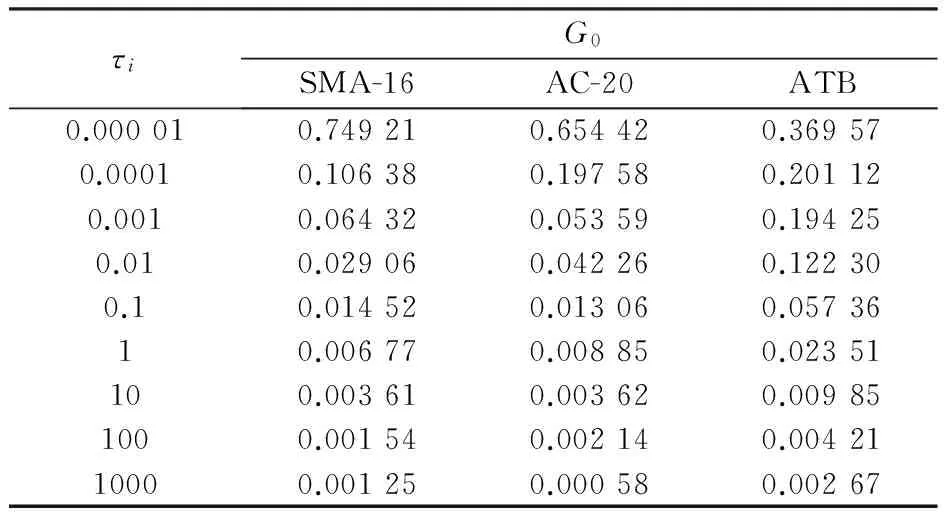
τiG0SMA-16AC-20ATB0.000010.749210.654420.369570.00010.106380.197580.201120.0010.064320.053590.194250.010.029060.042260.122300.10.014520.013060.0573610.006770.008850.02351100.003610.003620.009851000.001540.002140.0042110000.001250.000580.00267
采用WLF方程描述沥青路面材料对温度的依赖性:
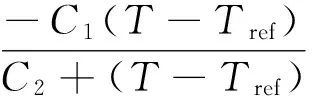
(2)
式中:αT为时温位移因子;C1、C2为回归系数;Tref为参考温度;T为测试温度。不同材料类型的WLF方程参数如表3所示。

表3 WLF方程参数
1.2 轮胎/路面静载接触印迹
轮胎与刚性路面接触时的横向和竖向接触应力分布可以准确表征相同类型的轮胎在沥青路面上行驶时所产生的结构应力及印迹分布[3-5]。通过ABAQUS软件模拟轮胎充气过程并进行模拟结果传递,将轮胎二维结构转化成三维结构,加入解析刚体路面,将路面6个自由度固定、轮辋与胎圈耦合,在轮辋中心处施加竖直向下的荷载,可获取轮胎(标准胎压)静止时在额定荷载作用下的变形,如图2所示。
图2 额定荷载下的轮胎变形
荷载和胎压变化时轮胎/路面接触印迹面积的变化呈现如下规律:①标准胎压下,随竖向荷载的增加,轮胎/路面接触面积不断增大,且接触印迹由近似椭圆形逐渐接近于矩形;②额定荷载下,随着胎压的不断增大,轮胎/路面接触印迹逐渐由矩形变为近似椭圆形。
1.3 轮胎/路面接触随机动荷载的简化表达
对轮胎、路面相互作用进行仿真分析时,轮胎荷载一般简化为竖向静荷载、移动恒载、简谐振动荷载或瞬时冲击荷载[6-9]。多个半正弦波形荷载的线性组合可代表由路面不平导致的荷载非线性变化。加之沥青路面材料具有黏弹性,带有一定恢复时间的半正弦荷载可以体现沥青路面的瞬时性和冲击性,荷载作用如图3所示。简化后的轮胎半正弦动荷载表达式为:
(3)
式(3)中:P0为静态均布荷载幅值;t为时间;T0为一个周期内半正弦荷载作用时间;Ta为荷载作用周期;n为荷载周期数。

图3 半正弦波荷载
1.4 模型网格划分
采用ABAQUS构建沥青路面三维结构有限元模型,路面结构深1600 mm,长2000 mm,宽2000 mm。对模型进行网格划分并在荷载作用区域加密网格,如图4所示,结构单元采用C3D8R单元,共14 880个。
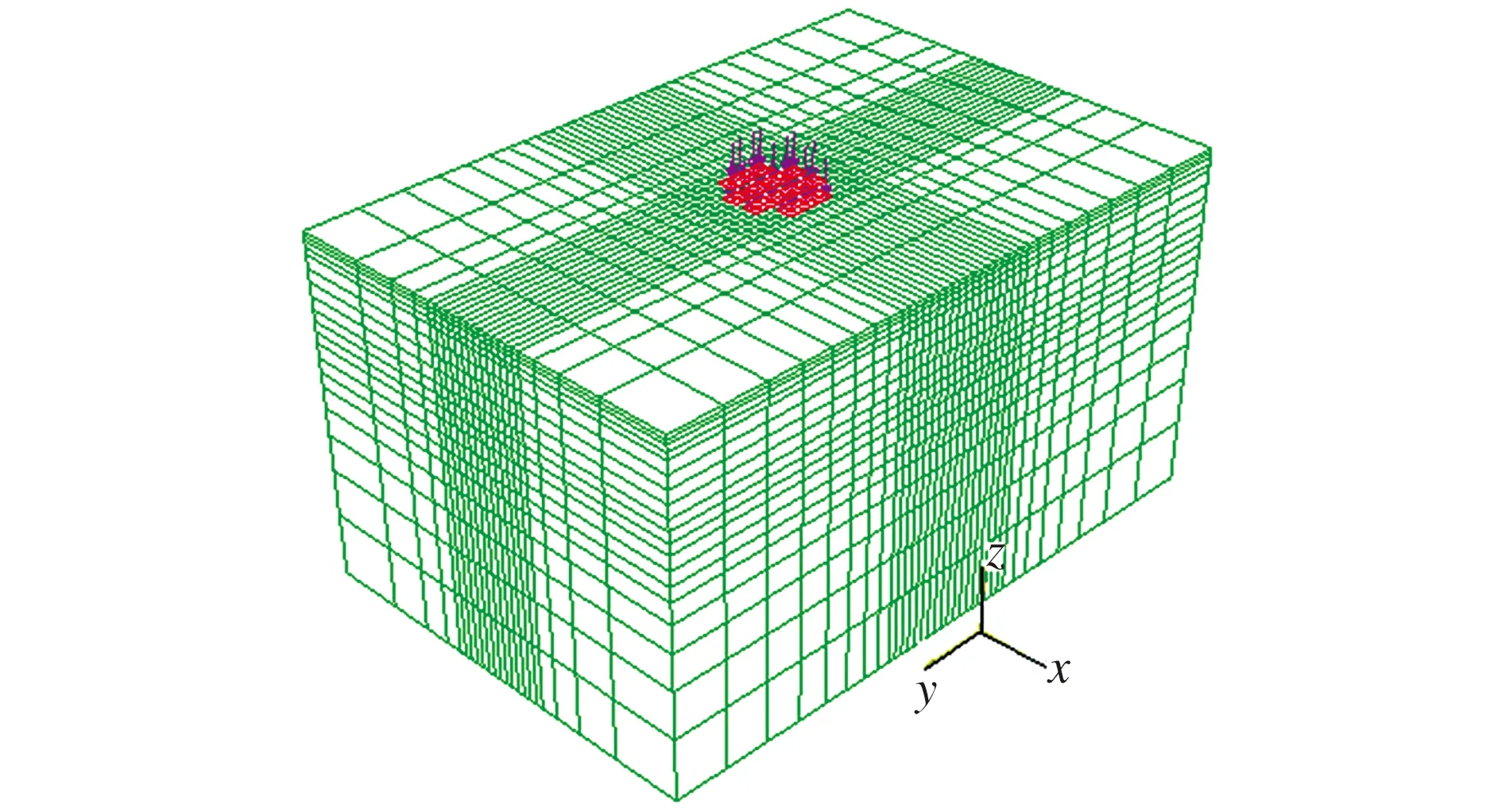
图4 沥青路面三维结构网格划分
1.5 分析方法与边界条件
有限元计算分解步骤如下:①构建轮胎与刚性路面接触模型,获取接触应力及标准胎压额定荷载作用下轮胎/路面接触的印迹特征;②轮胎/路面接触印迹简化后,确定沥青路面荷载受力面;③用简化半正弦荷载替代随机荷载施加于该沥青路面结构,获取沥青路面结构三向应力应变并进行分析。
荷载条件及路面结构边界如下:①轮胎接触面积内输入半正弦波荷载;②土基为半无限体,模型底面6个自由度固定;③前后面、左右面的法向位移为零。
2 路面结构力学响应分析
2.1 轮胎/路面接触印迹计算
轮胎型号为11.00R20-16PR,计算采用标准胎压和额定荷载。计算得到轮胎/路面接触印迹与简化后的有限元荷载作用面如图5所示,其中:L1、L2分别为轮胎最外缘花纹和中间花纹的接地长度,L1=76 mm,L2=223.8 mm;B1、B2分别为轮胎最外缘花纹接地宽度,B1=40.5 mm,B2=52 mm;w1、w2、w3为花纹间隙宽度,w1=w2=w3=8 mm。
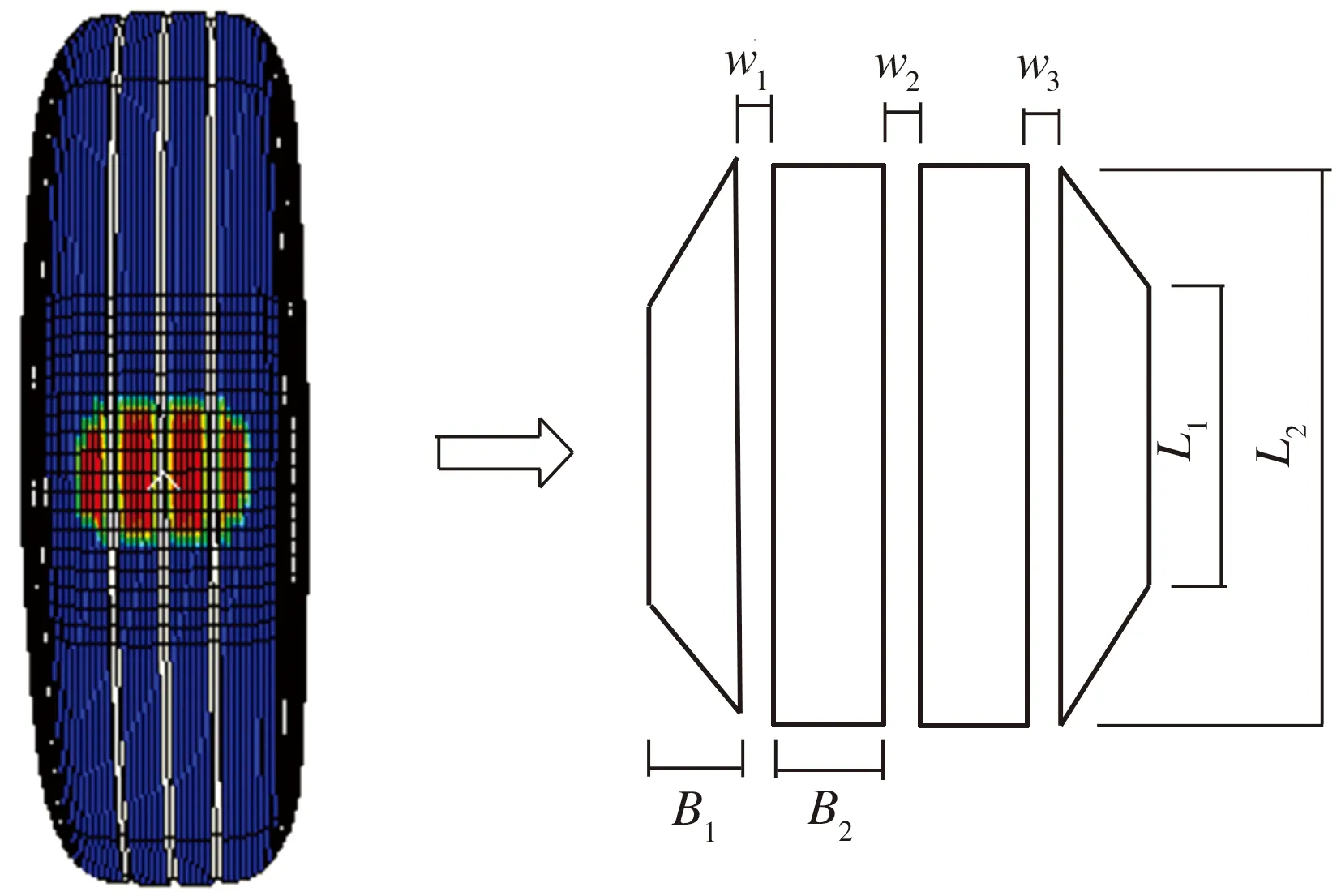
图5 轮胎/路面接触印迹及有限元荷载作用面
Fig.5Tire/pavementcontactmarkandloadingsurfaceinFEM
轮胎/路面有效接触面积为
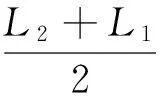
(4)
2.2 路面应力应变分析
在沥青路面结构受力区域中心部位分别选取深度方向(即z向)20、70、140、300 mm,同时,取路面结构与深度方向对应的上、中及下面层中部的水平位置x=20、50、150、200、250、300 mm处作为特征点,分析沥青路面结构的竖向、横向、纵向应力应变情况,其中,竖向垂直于路面方向,横向垂直于车轮行驶方向,纵向为行车方向。仿真计算时路面温度取为45 ℃。
2.2.1 竖向应力及应变
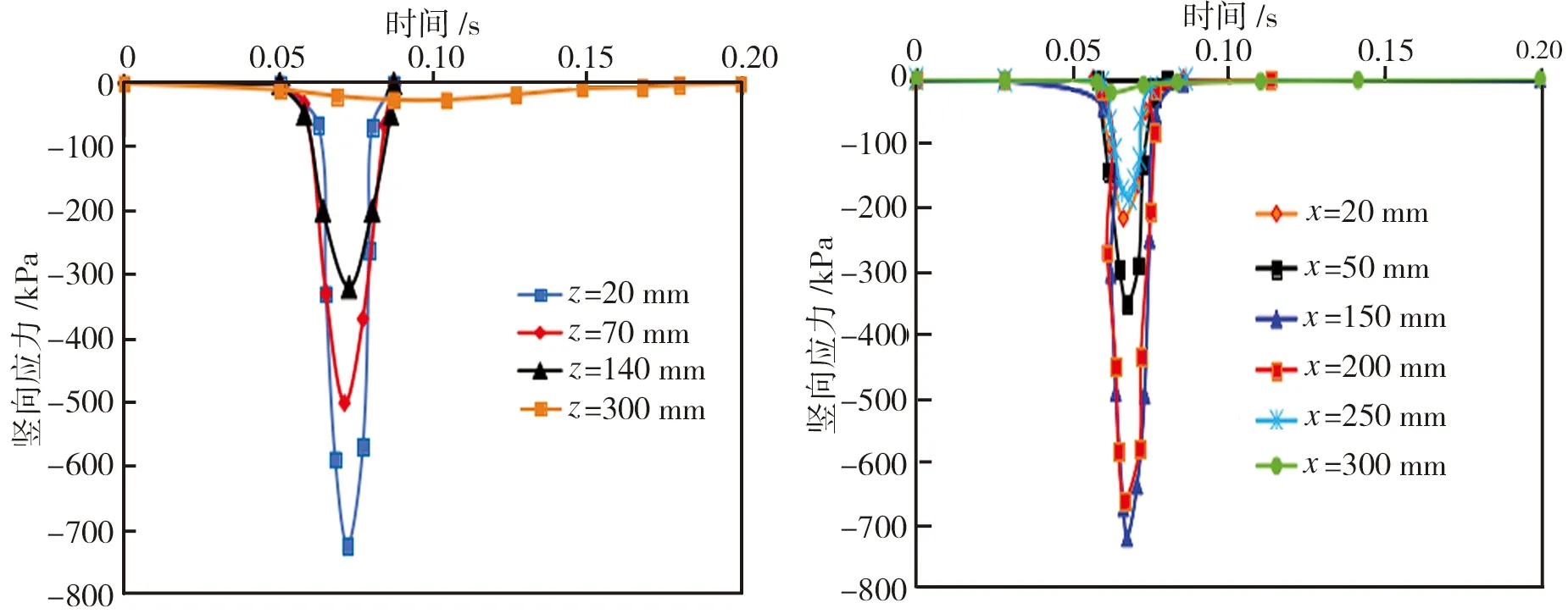
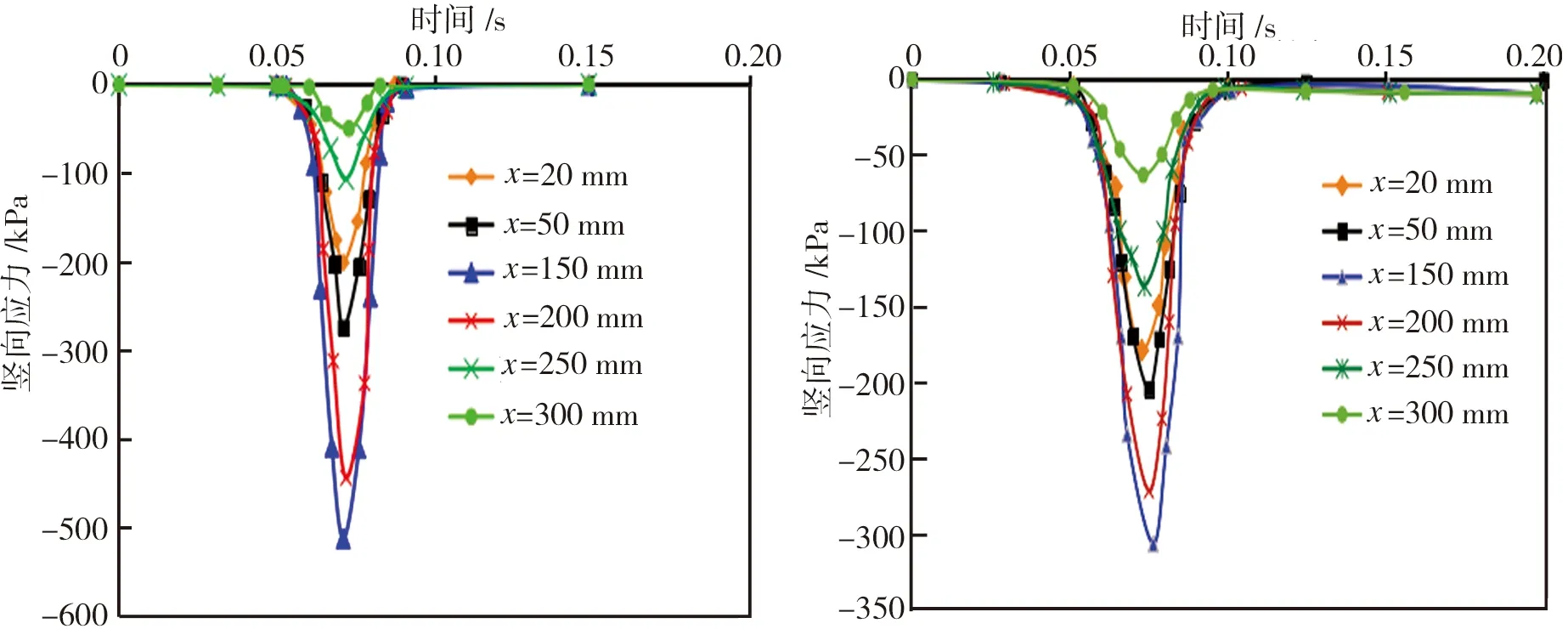
图6和图7分别为沥青路面竖向应力的时程曲线和云图。由图6可见,一个荷载周期内轮胎/路面接触印迹处的沥青路面竖向应力与荷载正相关。由图7可见,在荷载区域内上面层和中面层出现应力集中现象,且沥青路面上面层所受应力最大,随深度的增加应力值逐渐减小。
(a)荷载中部 (b)上面层中部
(c)中面层中部 (d)下面层中部
图6沥青路面竖向应力时程曲线
Fig.6Verticalstress-timecurvesoftheasphaltpavement
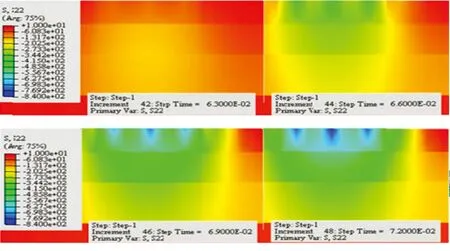
图7 沥青路面竖向应力云图
图8和图9分别为沥青路面竖向应变时程曲线和云图。由图8可见,一个荷载周期内,随着沥青路面深度的增加,其竖向应变幅值显著减小,同时在荷载减小为零后的一段时间内存在一定的残余应变,且沥青路面深度越浅应变恢复越慢;应变随荷载非线性增减而变化的曲线基本呈倒半正弦波状。由图9可见,在荷载作用范围内,沥青路面上面层呈现竖向应变集中,随路面深度的增加应变值逐渐减小。
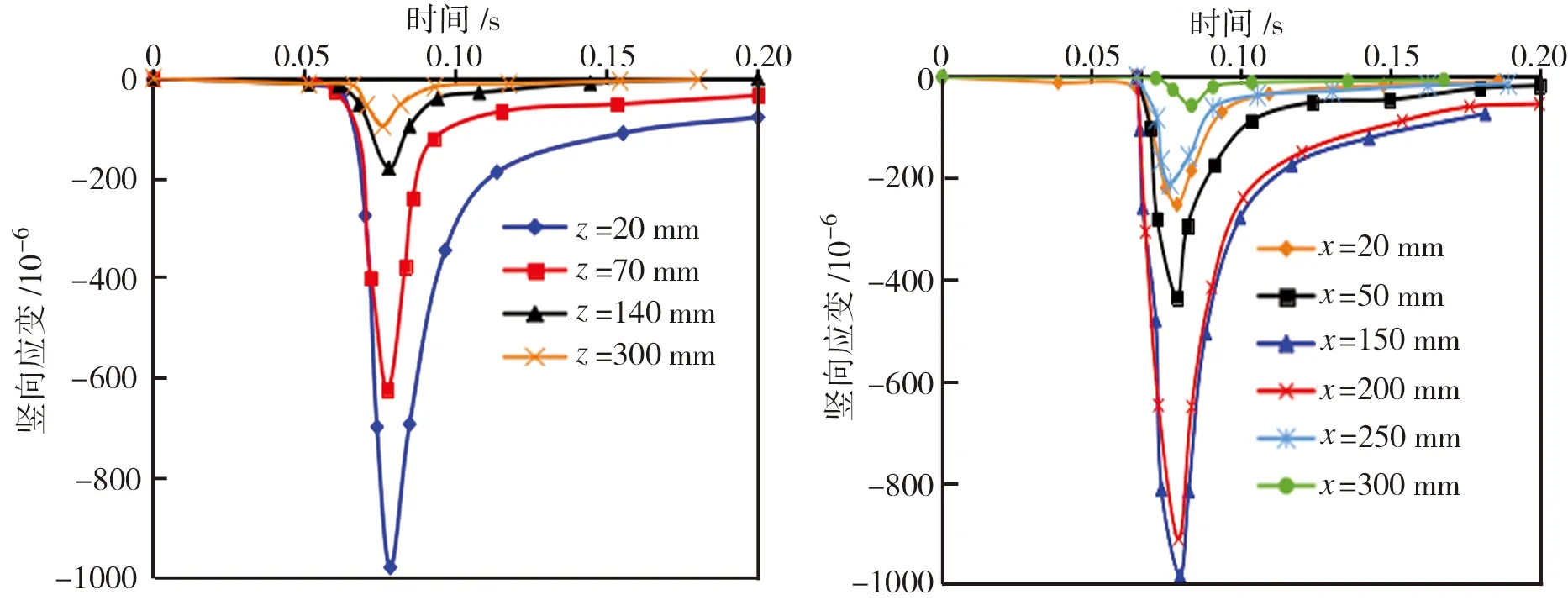
(a)荷载中部 (b)上面层中部
(c)中面层中部 (d)下面层中部
图8沥青路面竖向应变时程曲线
Fig.8Verticalstrain-timecurvesoftheasphaltpavement
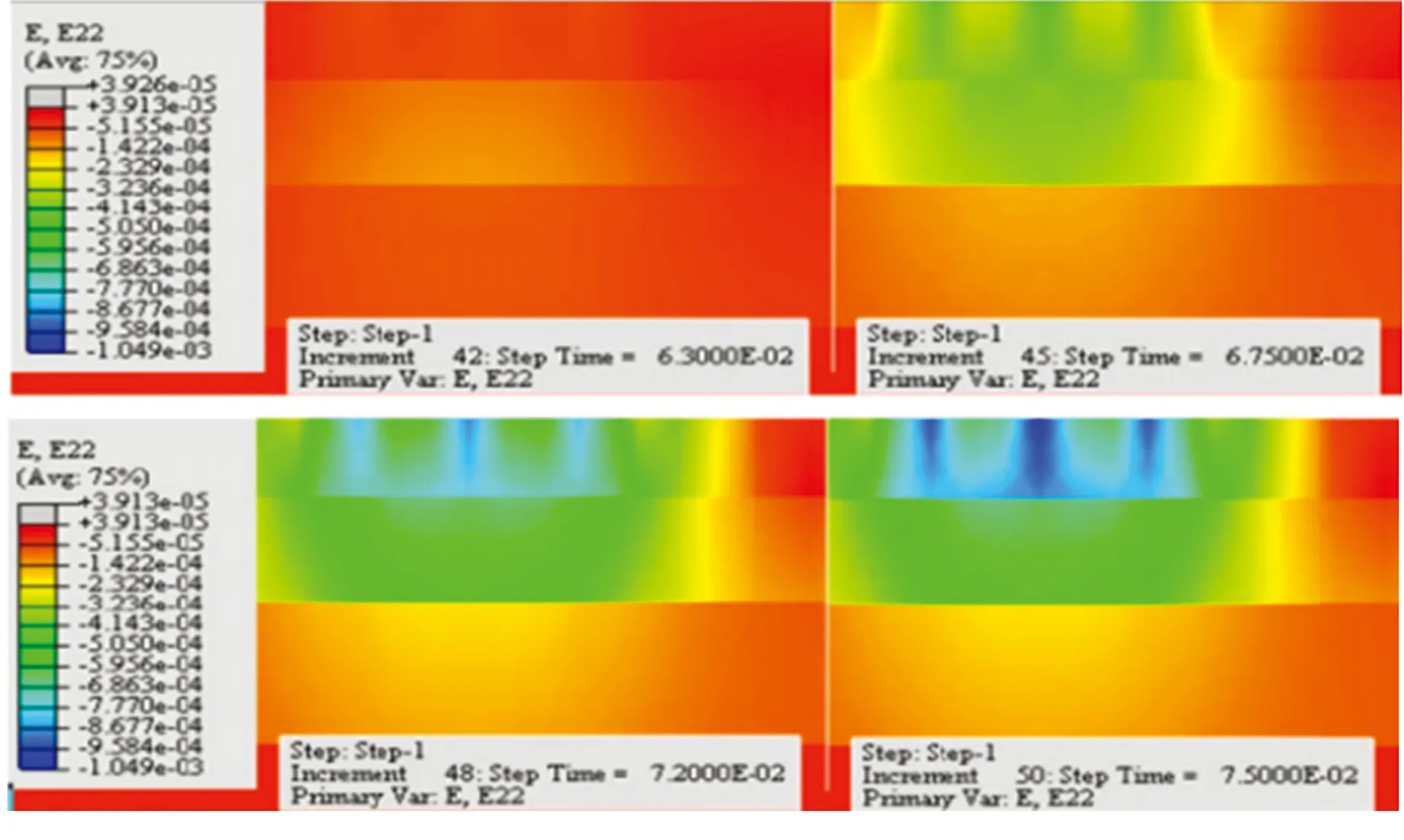
图9 沥青路面竖向应变云图
2.2.2 横向应力及应变
在轮胎/路面接触印迹范围内,沥青路面横向应力变化趋势与竖向应力变化趋势一致。在荷载区域内上面层、中面层和下面层同样都出现应力集中现象,且上面层所受应力最大;随路面深度的增加,横向应力逐渐减小。在此不重复讨论。
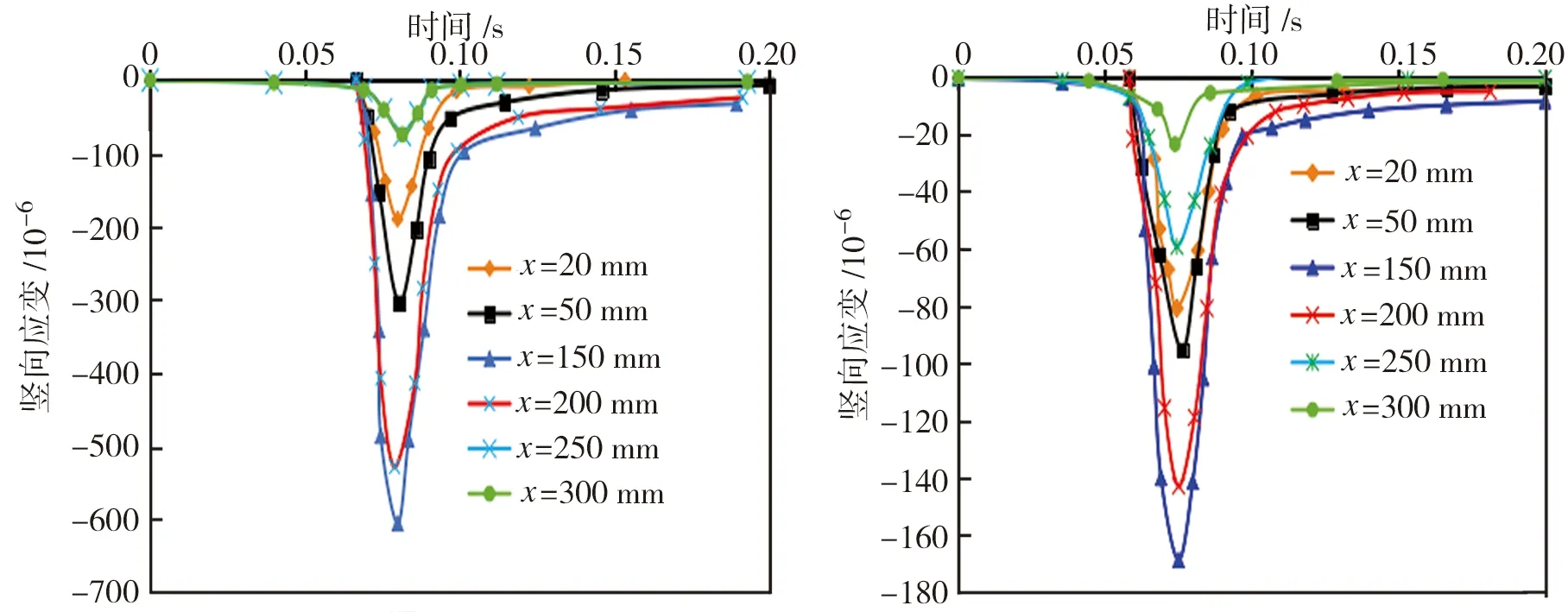
图10和图11分别为沥青路面横向应变时程曲线和云图。由图10可见,在一个荷载周期内,沥青路面横向应变随荷载变化先增大后减小,且与竖向应变类似,在荷载减小为零后还存在一定的残余应变,深度越浅应变恢复越慢。另外值得注意的是,荷载区域内出现横向拉应变,这是轮胎侧缘路面产生车辙等永久变形的原因之一。由图11可见,沥青路面横向应变在上面层和中面层出现应变集中,应变随深度的增加而减小。
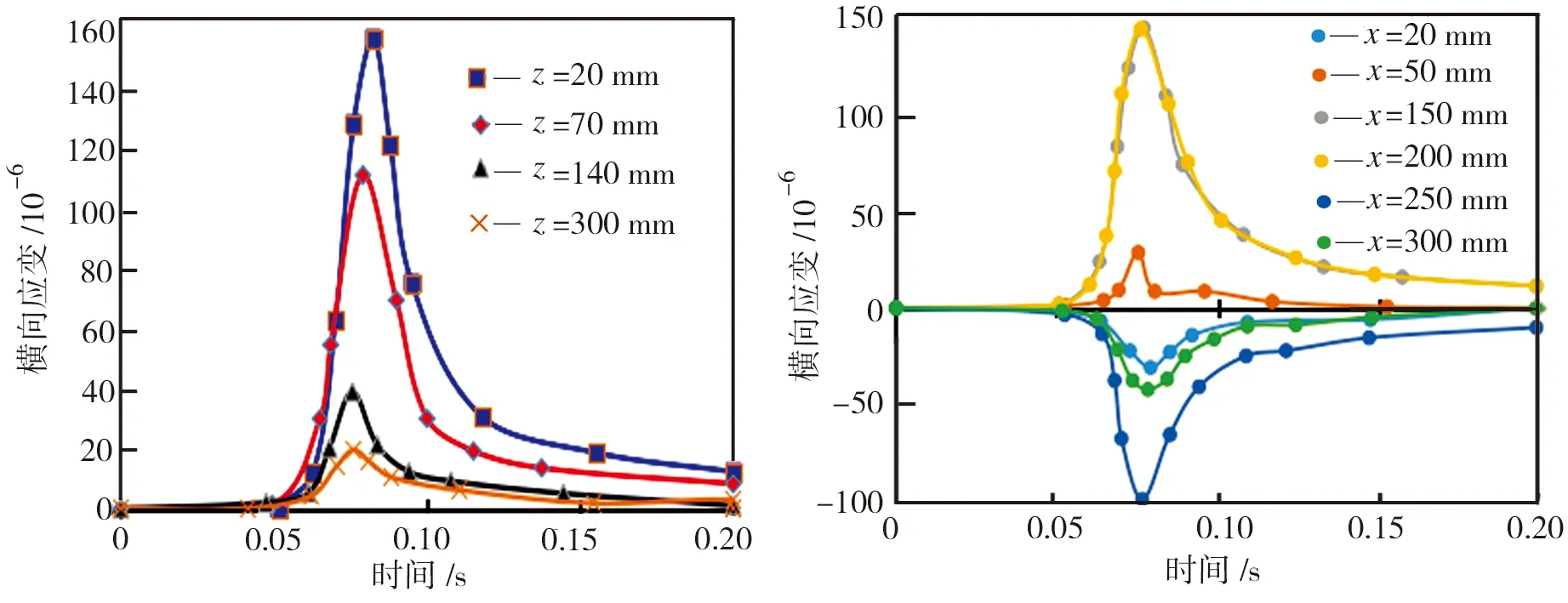
(a)荷载中部 (b)上面层中部

(c)中面层中部 (d)下面层中部
图10沥青路面横向应变时程曲线
Fig.10Transversestrain-timecurvesoftheasphaltpavement
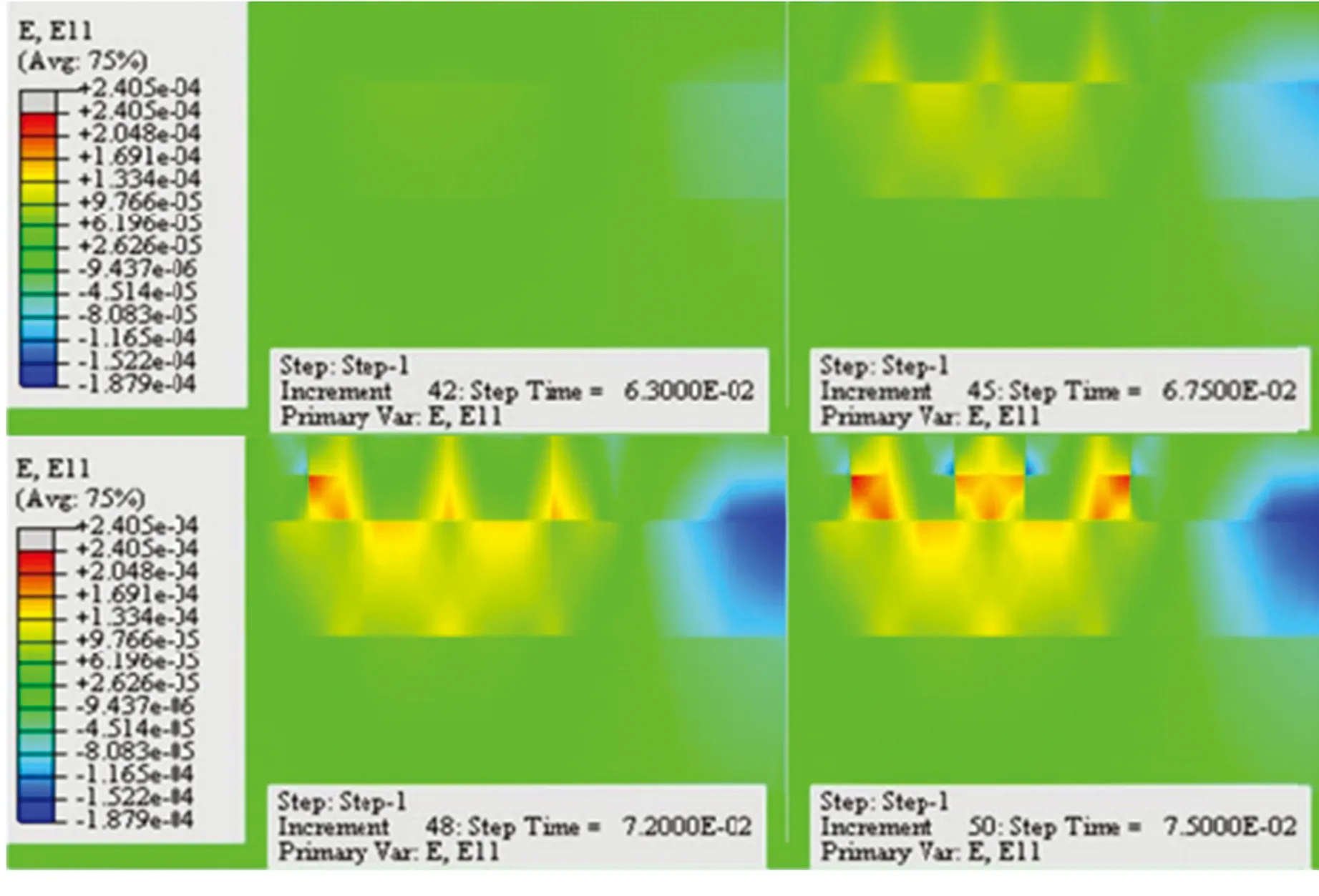
图11 沥青路面横向应变云图
2.2.3 纵向应力及应变
图12为沥青路面纵向应力时程曲线。由图12可见,随路面深度的增加纵向应力逐渐减小。同时,由于沥青路面的黏弹性,在轮胎接触印迹范围内随荷载非线性增加的过程中,由于上一时刻的残余应力影响,路面纵向应力出现微小的波动。

(a)荷载中部 (b)上面层中部
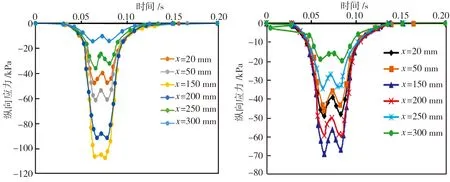
(c)中面层中部 (d)下面层中部
图12沥青路面纵向应力时程曲线
Fig.12Longitudinalstress-timecurvesoftheasphaltpavement
另外,由沥青路面纵向应力云图(限于篇幅,文中省略)可知,在荷载区域内上面层出现应力集中现象,且上面层所受应力最大;随着荷载的增加,中面层底部也出现应力集中。
图13和图14分别为沥青路面纵向应变时程曲线和云图。由图13和图14可见,不同深度处沥青路面纵向应变的变化趋势基本相同;纵向应变总体上随深度的增加而减小,但在上面层和中面层交界处出现纵向应变集中;纵向应变在一个荷载周期内出现拉压交替的变化情况,纵向上产生反复的拉压变形,极易导致路面材料发生疲劳损伤,进一步可表现为路面轮迹带从上至下的裂缝破坏。
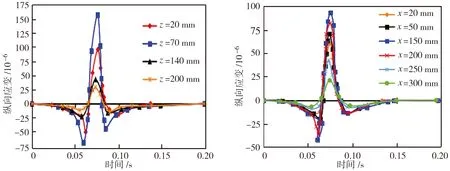
(a)荷载中部 (b)上面层中部
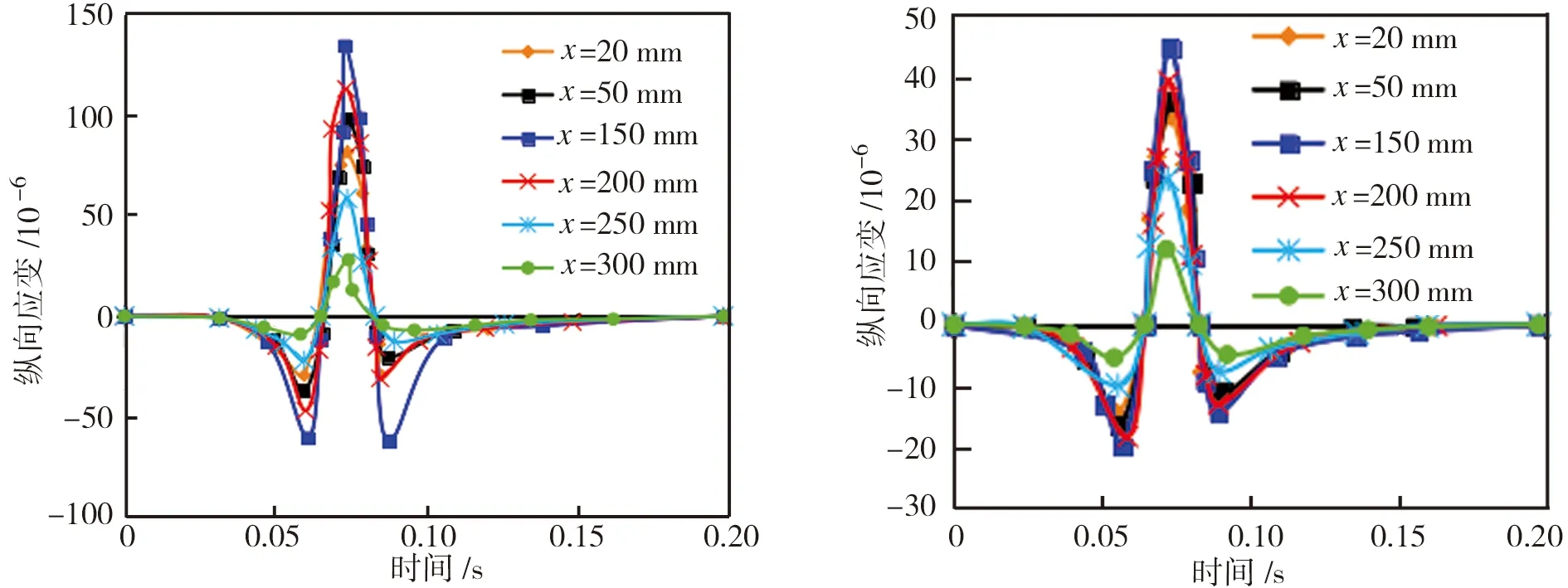
(c)中面层中部 (d)下面层中部
图13沥青路面纵向应变时程曲线
Fig.13Longitudinalstrain-timecurvesoftheasphaltpavement
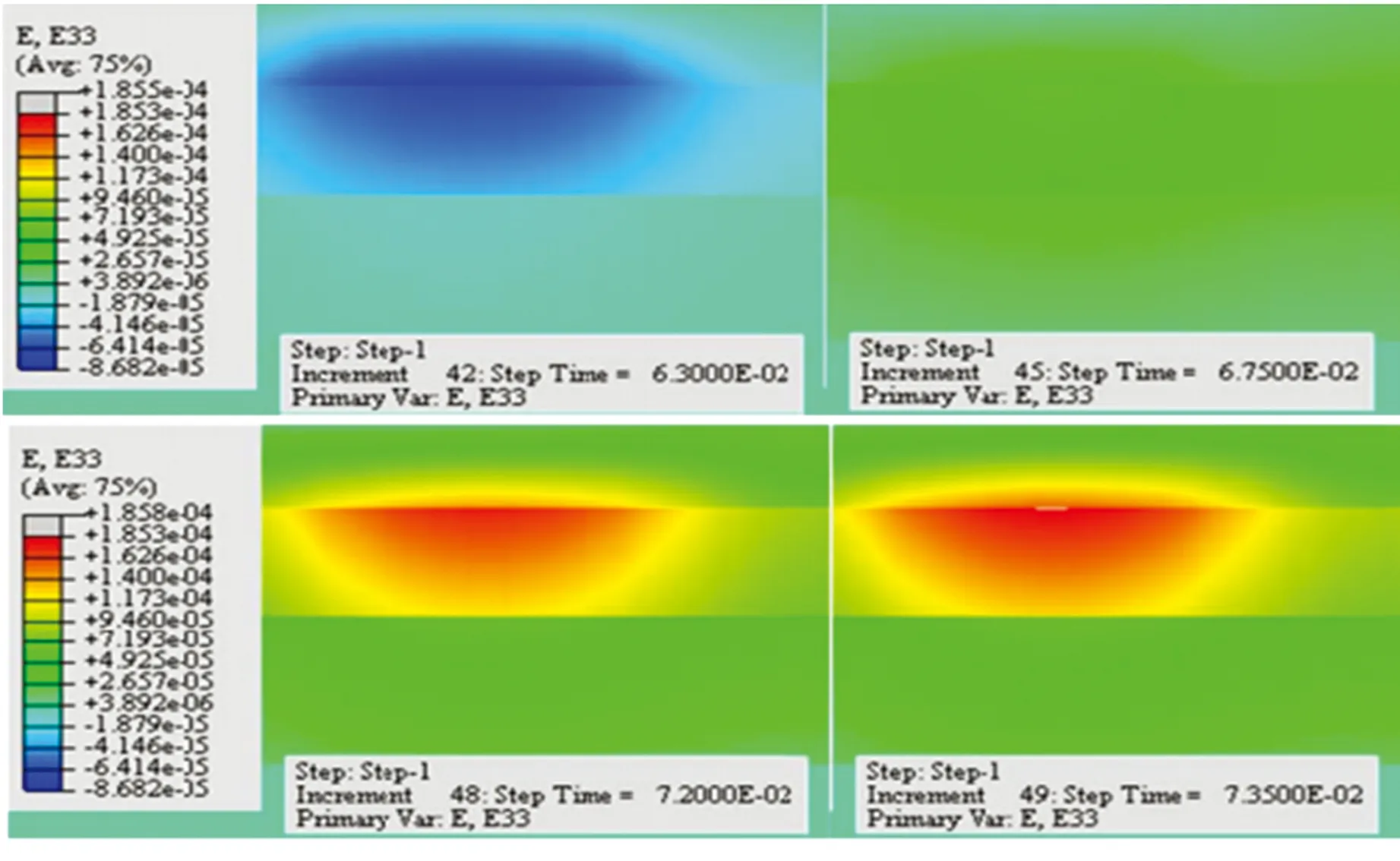
图14 沥青路面纵向应变云图
Fig.14Longitudinalstraincontoursoftheasphaltpavement
3 沥青路面力学响应影响因素分析
沥青路面力学响应受轮胎荷载、路面温度、荷载作用时间、路面结构类型、路面材料及路面不平度激励等多种因素影响。本文重点分析荷载作用时间和路面温度的影响。
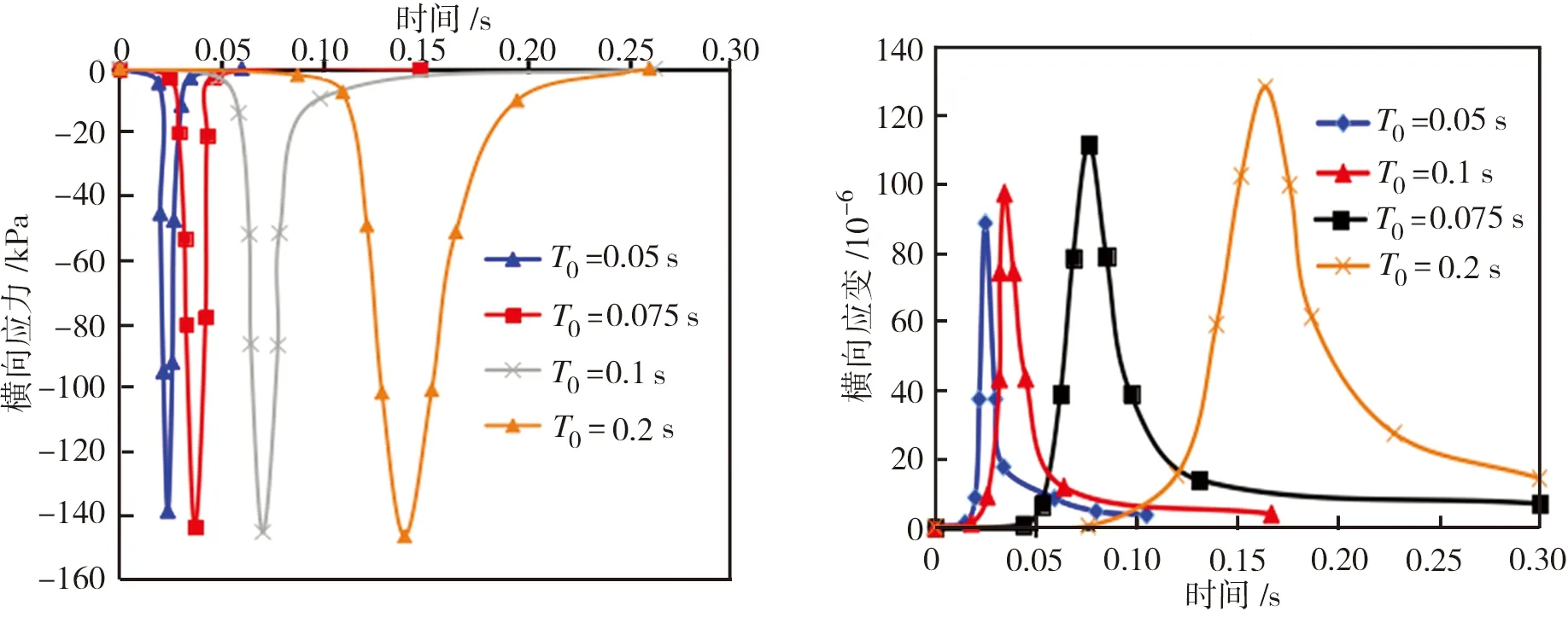
3.1 荷载作用时间
荷载作用时间不同时,路面温度45 ℃条件下荷载中心区域沥青路面中面层的竖向、横向及纵向应力应变时程曲线如图15所示。由图15可见,不同荷载作用时间下,竖向、横向及纵向应力变化趋势基本一致,应力幅值随荷载作用时间的缩短而略微减小,但竖向、横向及纵向应变的变化较大,即随着荷载作用时间的缩短,应变幅值的减小趋势较为明显。
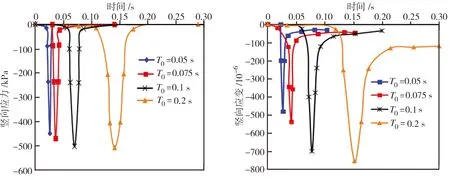
(a)竖向应力 (b)竖向应变
(c)横向应力 (d)横向应变

(e)纵向应力 (f)纵向应变
图15不同荷载作用时间下沥青路面的应力应变时程曲线
Fig.15Stress-timeandstrain-timecurvesoftheasphaltpavementatdifferentloaddurations
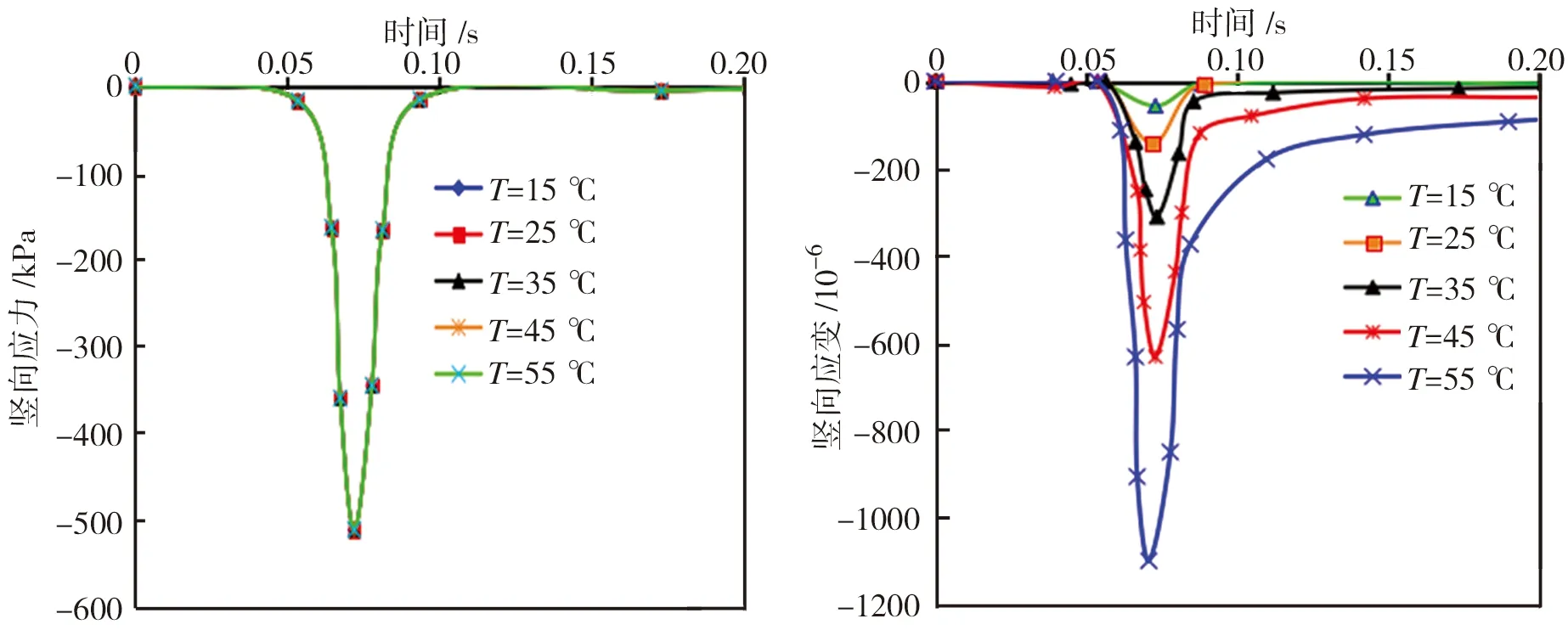
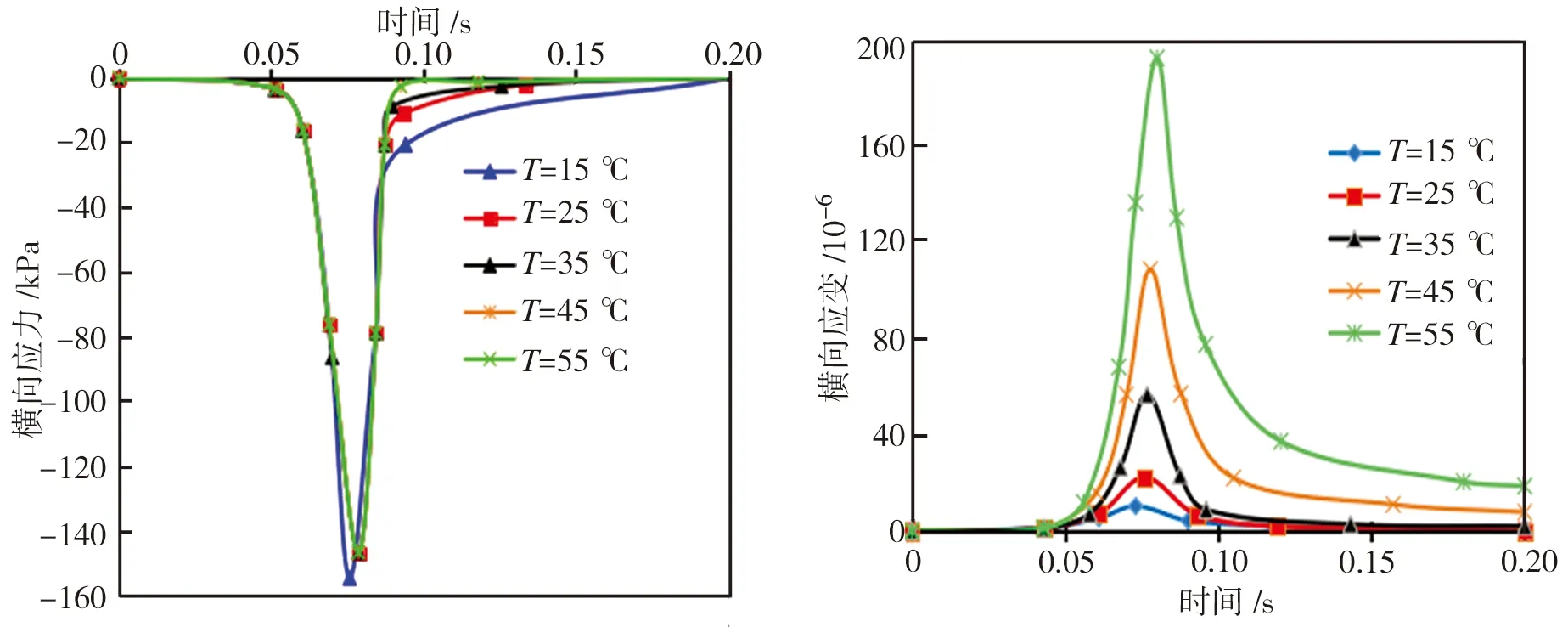
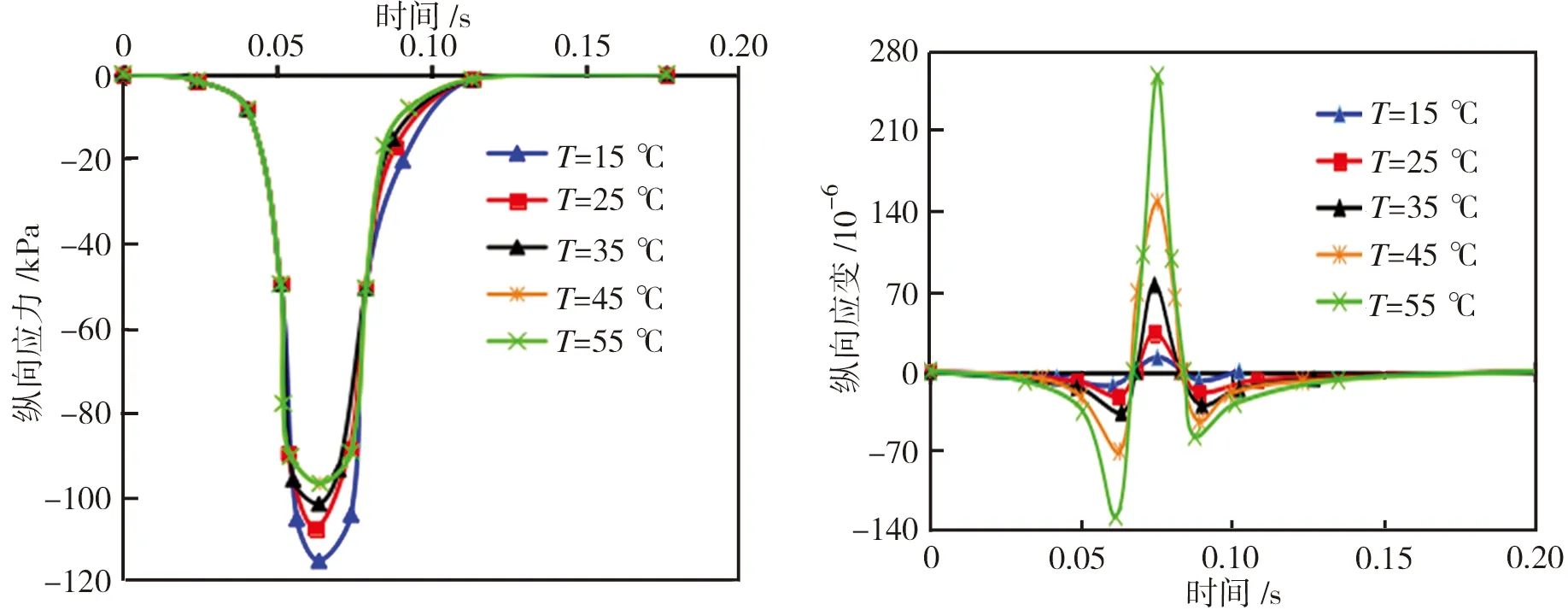
3.2 路面温度
以荷载中心处沥青路面中面层为分析点,得到不同温度时路面的竖向、横向、纵向应力应变时程曲线如图16所示。从图16中可以看出,不同温度下,沥青路面的竖向、横向和纵向应力基本相同,但随着温度的升高,竖向、横向和纵向应变幅值均逐渐增大,而且残余应变恢复时间延迟。可见,温度对沥青路面应变的影响较为显著。
(a)竖向应力 (b)竖向应变
(c)横向应力 (d)横向应变
(e)纵向应力 (f)纵向应变
图16不同温度下沥青路面的应力应变时程曲线
Fig.16Stress-timeandstrain-timecurvesoftheasphaltpavementatdifferenttemperatures
4 结论
(1)在半正弦荷载作用时程范围内,沥青路面荷载区的竖向、横向及纵向应力最大值均出现在上面层;同一特征点处,竖向应力幅值最大,横向应力幅值次之,纵向应力幅值最小。
(2)在半正弦荷载作用时程范围内,沥青路面的竖向和横向应变最大值出现在上面层,纵向应变在上面层和中面层交界处出现明显的应变集中;同一特征点处,竖向应变幅值最大,纵向应变幅值次之,横向应变幅值最小;沥青路面结构内部出现纵向的拉-压应变交替变化,且不同特征点处的纵向应变规律基本一致。总之,结构层间接触的非完全连续以及荷载作用下纵向反复的拉压变形,这可能是路面轮迹带产生裂缝损伤病害的重要原因。
(3)对于本文研究的路面结构形式,温度的升高使沥青路面的应变大幅上升,并延迟了残余应变的恢复时间;另外,随着半正弦荷载作用时间的缩短,应变幅值明显减小。因此,进行路面结构设计时应在现有控制指标的基础上合理使用应变指标。
[1] 谢水友.轮胎接触压力对沥青路面结构的影响研究[D].西安:长安大学,2003.
[2] 刘美丽.轮胎路面交互作用数值模拟分析[D].哈尔滨:哈尔滨工业大学,2013.
[3] 刘瑞军.移动荷载作用下沥青路面动响应分析[D].石家庄:石家庄铁道大学,2014.
[4] 康忠亮.车辆随机动载作用下柔性沥青路面的动态响应研究[D].青岛:青岛大学,2012.
[5] 刘萌成,黄晓明,陶向华.移动荷载作用下近桥台处路面结构动力响应的有限元法分析[J].公路交通科技,2006,23(5):1-6.
[6] 沙爱民,江晓霞.路面动态特性分析[J].交通运输工程学报,2001,1(2):63-67.
[7] 周华飞,蒋建群,毛根海.路面不平整引起的车辆动荷载分析[J].中国市政工程,2002(3):10-13.
[8] 于清,曹源文.不平整路面上的汽车动荷载[J].重庆交通学院学报,2003,22(4):32-34.
[9] 陶向华,黄晓明.车辆动载荷的频域模拟计算与分析[J].华中科技大学学报:城市科学版, 2003, 20(4):47-50.
[责任编辑尚晶]
Mechanicalresponsesofasphaltpavementunderhalf-sineload
LvYuejing,WeiCaixia,YingBaosheng,ZouLiqiong,ZhouXinglin,ZhangHusheng
(College of Automobile and Traffic Engineering, Wuhan University of Science and Technology, Wuhan 430081, China)
This paper studied the characteristics of tire/pavement contact mark and random load, established a three-dimensional finite element model of pavement structure by means of ABAQUS software and analyzed the mechanical responses of the asphalt pavement under half-sine load. The results show that stress and strain are concentrated in the top and middle layers of pavement structure under half-sine load and their values decrease with the increase of the pavement depth. Maximums of vertical, transverse and longitudinal stresses appear in the top layer of pavement structure, and vertical stress is the largest, followed by transverse then longitudinal stresses. Maximal vertical and transverse strains also appear in the top layer, but maximal longitudinal strain is in the top-middle layer and repeated tension-compression deformation in the longitudinal direction exists in the pavement structure which is likely the fundamental cause of material fatigue damage near the wheel path of asphalt pavements. In addition, load duration and pavement temperature have greater influences on the strain of asphalt pavement than on the stress. The rise of pavement temperature leads to the increase of strain and delays the recovery of residual strain.
asphalt pavement; mechanical response; half-sine load; finite element analysis; tire/pavement contact mark; stress-strain
U416.217
A
1674-3644(2017)06-0457-07
2016-09-13
国家自然科学基金资助项目(51578423);国家自然科学基金青年科学基金资助项目(51508428).
吕悦晶(1979-),女,武汉科技大学副教授,博士.E-mail:lvyuejing@126.com
10.3969/j.issn.1674-3644.2017.06.010

