二自由度关节型机器人的自适应模糊滑模控制
杜 峰,孙 瑛,2,李公法,2,李 喆,孔建益,2,蒋国璋,2,江 都
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081;3.武汉船舶设计研究院有限公司,湖北 武汉,430064)
二自由度关节型机器人的自适应模糊滑模控制
杜 峰1,孙 瑛1,2,李公法1,2,李 喆3,孔建益1,2,蒋国璋1,2,江 都1
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081;3.武汉船舶设计研究院有限公司,湖北 武汉,430064)
针对二自由度关节型机器人控制问题,通过分析传统滑模控制的不足,提出一种自适应模糊滑模控制算法。采用自适应单输入单输出模糊系统来计算控制增益,同时设计了基于Lyapunov稳定性理论的自适应律,最后利用Simulink软件对自适应模糊滑模控制进行仿真实验。结果表明,机器人各关节控制力矩的抖振现象明显减弱,系统性能得到提升;自适应算法的加入使模糊滑模控制能在短时间内随着系统状态的变化自动地进行调节,稳态收敛为常数;在关节型机器人参数不确定和存在外界干扰的情况下,自适应模糊滑模控制算法依然具有良好的鲁棒性和跟踪精度。
关节型机器人;二自由度;滑模控制;模糊控制;自适应控制;抖振;仿真
为了使机器人能够跟踪给定轨迹,一般是通过对其各关节的驱动力矩进行控制。根据已知的机器人结构和相关参数,可以用机器人数学模型来描述其动态特征,但在实际应用中通常很难得到准确的数学模型,而会对某些不确定的影响因素做相应处理。目前在非线性、不确定性机器人系统中,滑模控制方法得到了广泛的应用和发展[1-3]。滑模控制的变结构特点体现在系统结构是随着系统状态而变化的,这种结构使系统可以沿着滑模面附近轨迹运动。因为滑模控制与系统的参数摄动及外界干扰无关,所以它的一个显著优点是鲁棒性较好。但是,滑模控制的不连续性会使系统产生抖振现象[4-5]。抖振会影响系统控制的精确性,增加系统能量消耗,甚至会激发系统未建模部分的强烈振动从而危害系统[6],因此如何削弱抖振是滑模控制研究的重要问题,而将多种控制方法相结合是近年来采用较多的研究思路[7-8]。
本文将自适应控制、模糊控制和滑模控制相结合,应用于二自由度关节型机器人控制中,以达到对滑模控制系统中增益的自适应调整目的,从而减弱系统抖振,使机器人能平稳、高精度运行。
1 传统滑模控制方法
1.1 二自由度关节型机器人建模
二自由度关节型机器人如图1所示。图中,g为重力加速度;连杆1的长度为l1,质量为m1,其质心到关节1的长度为lc1,转动惯量为I1;连杆2连同负载可以视为一个整体,其质量为me,转动惯量为Ie,质量中心到关节2的距离为Ice,质量中心与连杆2的夹角为δe。
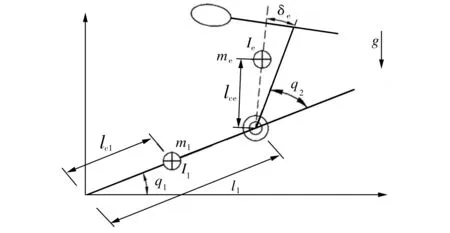
图1 二自由度关节型机器人示意图
多关节机器人系统动力模型表达式为:
(1)

对于二自由度关节型机器人系统,有
(2)
其中:
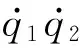
1.2 传统滑模控制律的设计
定义跟踪误差为:
e=qd-q
(3)
式中:qd为需要跟踪的关节角位移矢量。
设计滑模函数为:
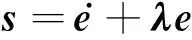
(4)
式中:λ=diag[λ1,…,λn],λi(i=1,2,…,n)为正常数。
通过选择控制输入τ来实现控制目标,以使滑动面满足充分条件:
(5)
式中:ηi为正常数。
式(5)表明滑动面的能量只要不为零就会一直衰减。为了建立τ,定义参考状态:
(6)
(7)
设计控制律为:

(8)
将式(8)代入式(1)得:
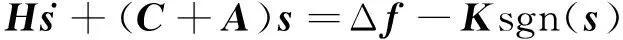
(9)
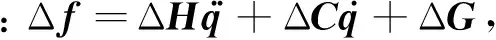
假设|Δfi|<|Δfi|bound,取
Kii≥|Δfi|bound
(10)
为了证明系统的稳定性,选择Lyapunov候选函数为:

(11)
由于H是对称和正定的,且s≠0,V>0,可以证明:
Kiisgn(si))]-sTAs≤-sTAs≤0
(12)
式(11)可以作为s能量的一种指标。因此,式(12)保证了当s≠0时其能量的衰减,满足式(5)中的充分条件。
1.3 仿真实验
确定参数:m1=1.0,l1=1.0,lc1=0.5,I1=0.0833,me=3.0,lce=1.0,Ie=0.4,δe=0。采用Simulink软件对二自由度关节型机器人进行传统滑模控制仿真,结果如图2、图3所示。
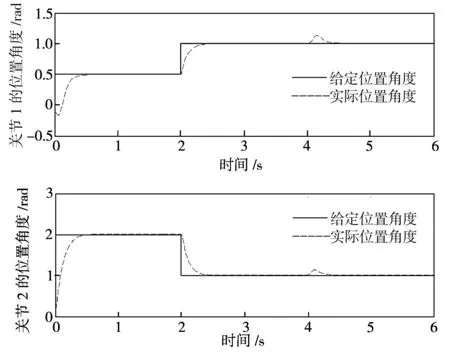
图2 关节1 和关节2 的位置跟踪情况
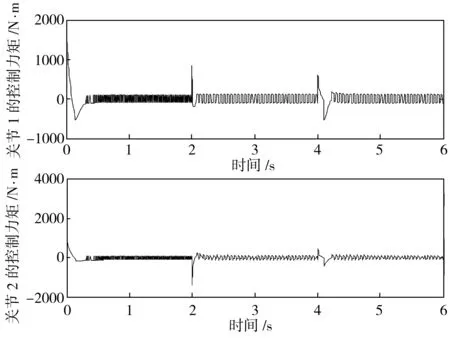
图3 关节1 和关节2 的控制器输出力矩
整个仿真过程分为两个阶段。第一阶段,关节型机器人从初始位置到达位置1,停留一段时间,然后在t=2 s时从位置1向位置2移动。第二阶段,在t=4 s时对机器人施加扰动,在t=4.1 s时取消扰动。由以上过程可知,系统状态在机器人开始向位置1移动和在第2 s向位置2移动时发生改变。由于在第4 s时施加了扰动,系统状态再次改变,取消扰动时系统回到了动态平衡。因此,整个过程中系统状态改变了3次。
由图2可见,传统滑模控制算法能使机器人在短时间内较好地跟踪预先给定曲线。然而由图3可知,各关节滑模控制器输出力矩存在明显的抖振现象,这是本文需要解决的主要问题。
2 自适应模糊滑模控制算法设计
2.1 模糊控制器基本结构
图4为本研究中模糊控制器的基本结构,主要包括乘积推理机、单值模糊器以及中心平均解模糊器等。系统的输出表示为[9]:
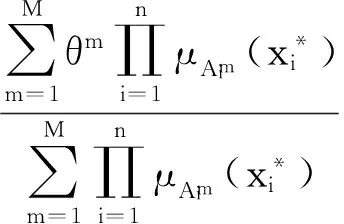
(13)
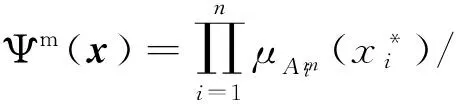
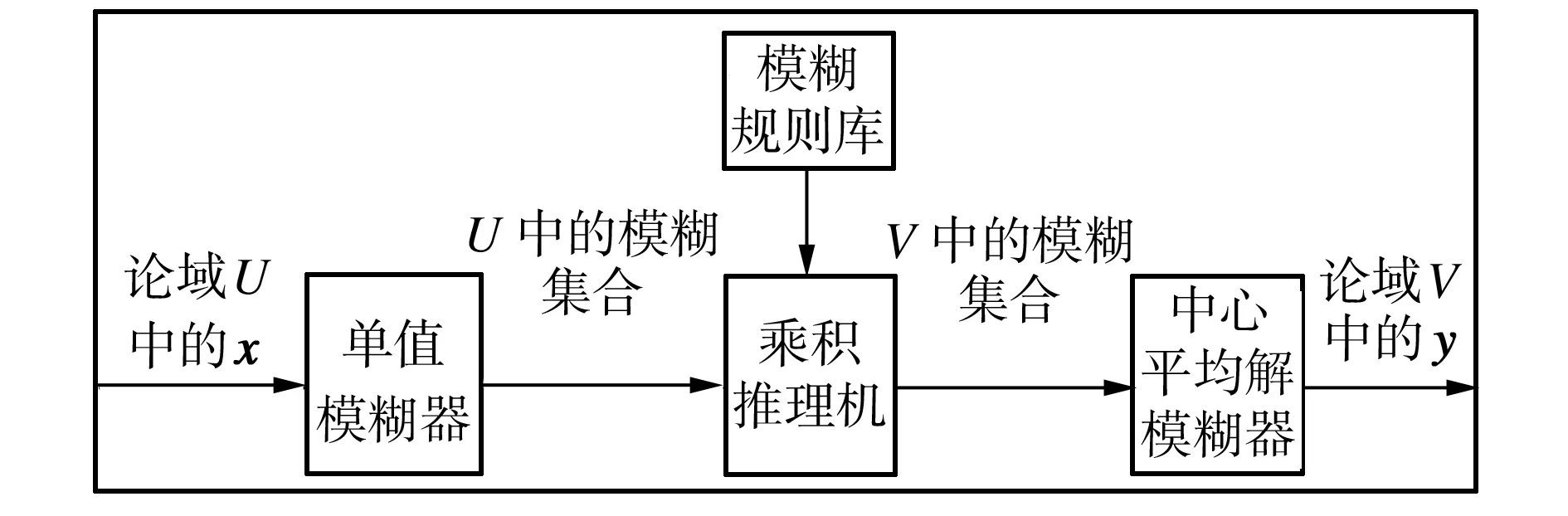
图4 模糊控制器的结构
2.2 自适应模糊滑模控制器设计
抖振问题的产生源于定值K和不连续函数sgn(s),因此这里用模糊增益k替换控制增益K。控制输入可写为:
(14)
式中:k=[k1,…,ki,…,kn],其中每个元素由一个单独的模糊系统来估计。
2.2.1 规则库的提取
系统的不确定性和s能量的减少是由模糊增益k来补偿的。这种情况下,设计模糊规则库为:当si增大时,ki值也增大;当si减小时,只要|ki|>|Δfi|,ki值可以减小;当si为零时,ki值取零。模糊规则库如表1所示,其中,N代表负,P代表正,B代表大,M代表中等,S代表小,ZE代表零。

表1 模糊规则库
在上述规则中,si和ki的隶属度函数的类型和名称相同,但隶属度函数对应的中心和宽度不同。此外,该控制器的自适应性体现在:si隶属度函数的参数是预先定义的,而ki隶属度函数的参数是在线更新的[10]。
2.2.2 控制律的设计
将式(14)代入式(1),得:
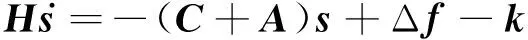
(15)
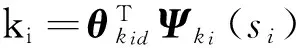
(16)
其中ωi可以尽量小。定义
(17)
则
(18)
选择自适应律为:
(19)
选择Lyapunov候选函数为:
(20)
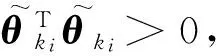
(21)
将式(19)代入式(21),得
(22)
存在很小的正实数γi,使得式(16)满足:
(23)
且式(22)等号右边第二项满足:
(24)
因此
(25)
式中:γ=diag[γ1,…,γi,…γn]。为简化起见,选择ai>γi,以使(A-γ)为一个正定矩阵,则
(26)
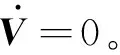
2.3 仿真实验
自适应模糊滑模控制系统结构如图5所示,二自由度关节型机器人的自适应模糊滑模控制仿真结果如图6~图8所示。仿真条件与前述传统滑模控制仿真相同。
从图6可以看出,自适应模糊滑模控制算法和传统滑模控制算法一样具有良好的跟踪性能。从图7可以看出,通过自适应模糊系统对传统滑模控制中切换增益的逼近,消除了输出力矩的抖振现象,提升了系统性能。由图8可见,自适应算法的加入使模糊滑模控制能在短时间内随着系统状态的变化自动地进行调节,稳态收敛为常数。总之,针对关节型机器人参数不确定和存在外界干扰的情况,自适应模糊滑模控制算法依然具有良好的鲁棒性和跟踪精度,由于其控制结构简单,计算效率高,无需实时确定机器人的运动参数,因此适用于关节型机器人的实时控制场合。
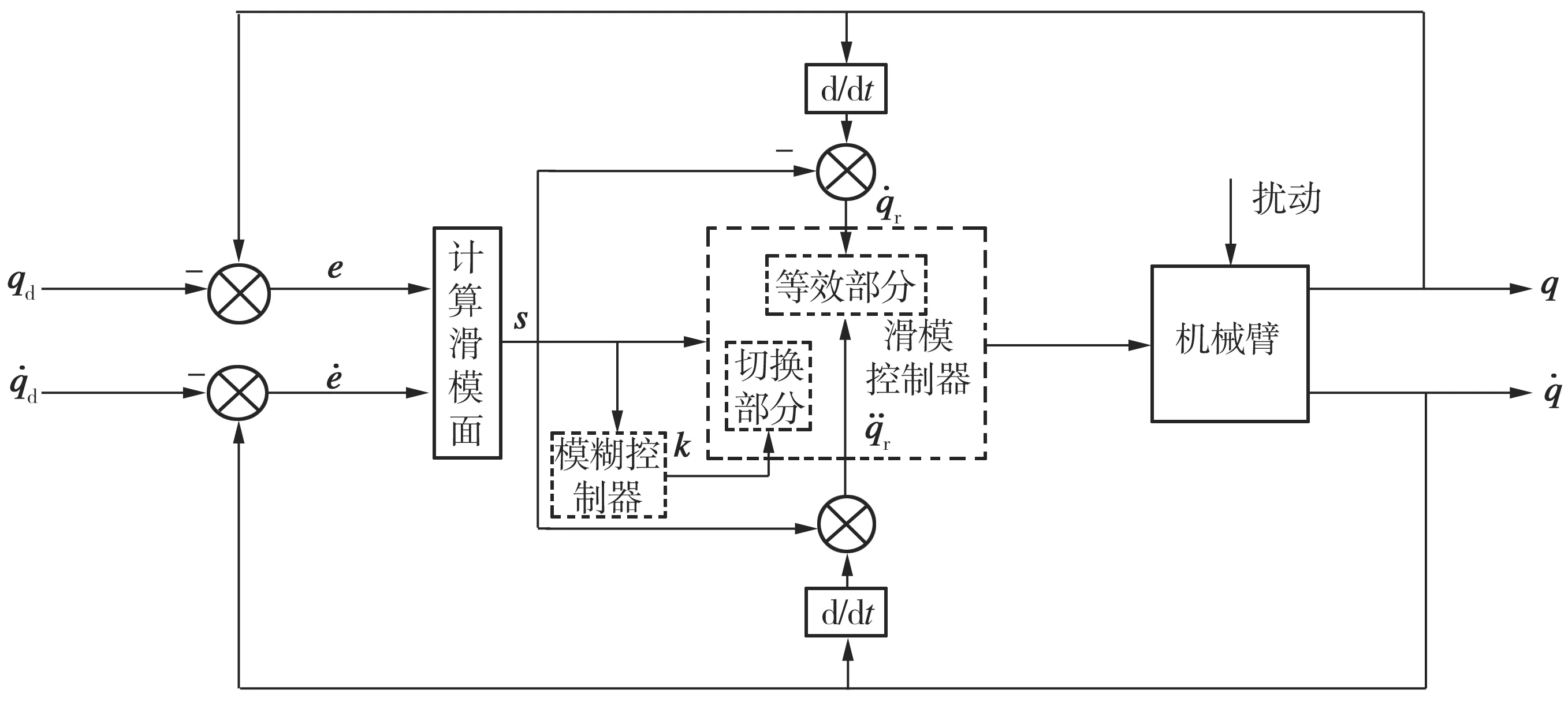
图5 自适应模糊滑模控制系统结构
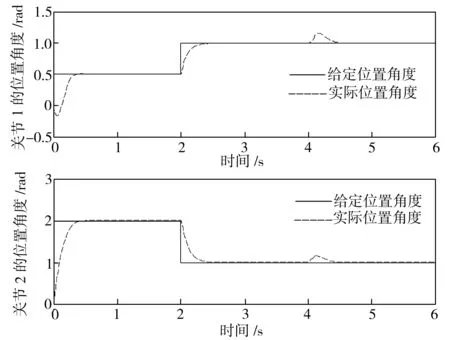
图6 关节1 和关节2 的位置跟踪情况
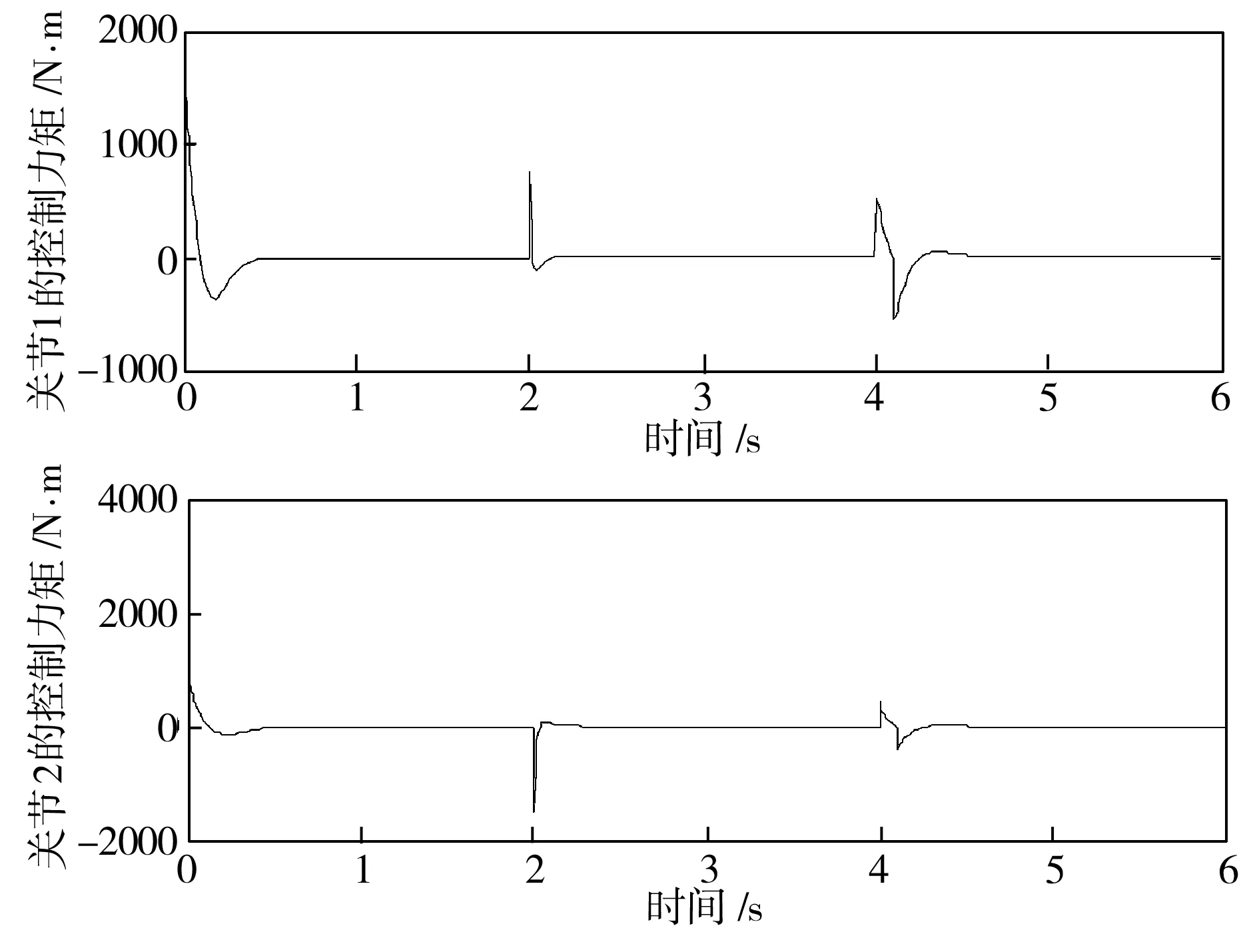
图7 关节1 和关节2 的控制器输出力矩
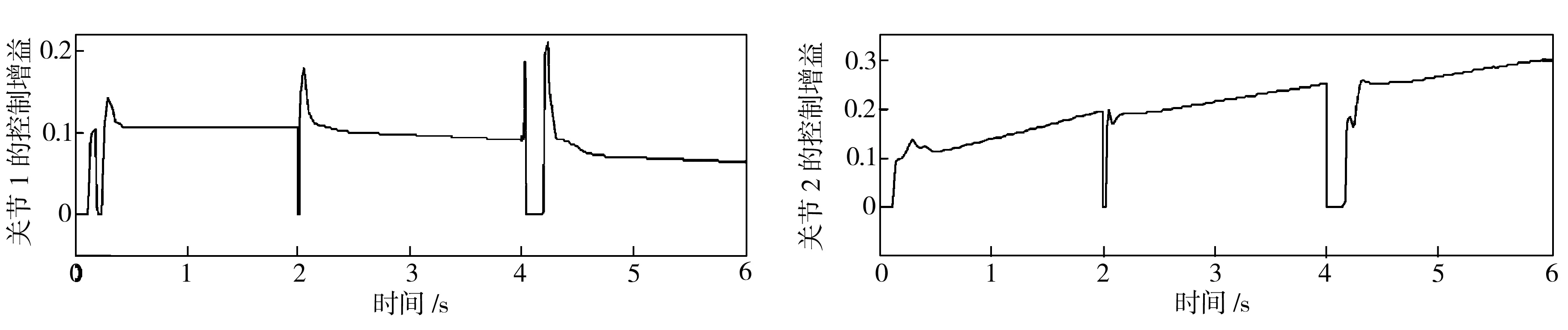
图8 自适应模糊滑模控制的增益变化
3 结语
本文提出了一种二自由度关节型机器人的自适应模糊滑模控制算法,其中控制增益及其隶属度函数是实时更新的,以补偿系统的不确定性未知参数,无需其先验知识,系统的稳定性也能得到保证。此外,由于控制器的模糊系统是单输入单输出系统,规则数相对于多输入系统来说更少,所以控制器的设计和实现更加容易。文中对控制系统的稳定性和收敛性进行了理论证明。仿真实验结果也表明,在给定的工况和干扰条件下,自适应模糊滑模控制在保证机器人跟踪精度的同时,使控制力矩的抖振现象得到明显改善,因此该控制方法是可行和有效的。
[1] 刘金琨,孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用,2007,24(3):407-418.
[2] 武俊峰,李月.滑模变结构方法在两轮自平衡机器人上的应用[J].哈尔滨理工大学学报,2013, 8(2):95-100.
[3] Rossomando F G, Soria C M. Adaptive neural sliding mode control in discrete time for a SCARA robot arm[J].IEEE Latin America Transactions, 2016, 14(6):2556-2564.
[4] Hashem Zadeh S M, Khorashadizadeh S, Fateh M M, et al. Optimal sliding mode control of a robot manipulator under uncertainty using PSO[J]. Nonlinear Dynamics, 2016, 84(4):2227-2239.
[5] Zhu S Q, Jin X L, Yao B, et al. Non-linear sliding mode control of the lower extremity exoskeleton based on human-robot cooperation[J]. International Journal of Advanced Robotic Systems, 2016, 13(5):1-10.
[6] Zhu S Q, Chen Q C, Wang X Y, et al. Dynamic modelling using screw theory and nonlinear sliding mode control of serial robot[J]. International Journal of Robotics and Automation, 2016, 31(1):63-75.
[7] Al-khazraji A, Essounbouli N, Hamzaoui A, et al. Type-2 fuzzy sliding mode control without reaching phase for nonlinear system[J]. Engineering Applications of Artificial Intelligence, 2011, 24(1):23-38.
[8] Aloui S, Pagès O, El Hajjaji A, et al. Improved fuzzy sliding mode control for a class of MIMO nonlinear uncertain and perturbed systems[J]. Applied Soft Computing, 2011,11(1):820-826.
[9] He J, Luo M Z, Zhang X L, et al. Adaptive fuzzy sliding mode control for redundant manipulators with varying payload[J]. Industrial Robot, 2016, 43(6):665-676.
[10] 胡盛斌,陆敏恂.空间三关节机器人自适应双模糊滑模控制[J].同济大学学报:自然科学版,2012,40(4):622-628.
[责任编辑尚晶]
Adaptivefuzzyslidingmodecontrolfor2-DOFarticulatedrobot
DuFeng1,SunYing1,2,LiGongfa1,2,LiZhe3,KongJianyi1,2,JiangGuozhang1,2,JiangDu1
(1.Key Laboratory of Metallurgical Equipment and Control Technology of Ministry of Education, Wuhan University of Science and Technology, Wuhan 430081, China; 2.Hubei Key Laboratory of Mechanical Transmission and Manufacturing Engineering, Wuhan University of Science and Technology, Wuhan 430081, China; 3.Wuhan Ship Development and Design Institute Co., Ltd., Wuhan 430064, China)
Aimed at the control of 2-DOF articulated robot, an adaptive fuzzy sliding mode control algorithm is proposed after analyzing the deficiency of classical sliding mode control method. An adaptive single-input single-output fuzzy system is applied to calculate the control gain and adaptive laws are designed based on Lyapunov stability theory. Then the adaptive fuzzy sliding mode control is simulated using Simulink software. The results show that the chattering of control torque for the joints of the robot is significantly weakened, and the system performance is improved. Fuzzy sliding mode controller can be automatically adjusted with the transformation of system state because of the adaptive algorithm, and the steady state converges to a constant. In the case of articulated robot with uncertain parameters and external disturbance, the proposed algorithm still has good robustness and high tracking precision.
articulated robot; two degree of freedom; sliding mode control; fuzzy control; adaptive control; chattering; simulation
TP273
A
1674-3644(2017)06-0446-05
2017-06-16
国家自然科学基金资助项目(51575407, 51575338, 51575412).
杜 峰(1992-),男,武汉科技大学硕士生.E-mail: 305048751@qq.com
李公法(1979-),男,武汉科技大学教授,博士生导师.E-mail: ligongfa@wust.edu.cn
10.3969/j.issn.1674-3644.2017.06.008

