高压圆盘气体轴承可压缩边界层形态分析
刘 剑,郭良斌,2
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081)
高压圆盘气体轴承可压缩边界层形态分析
刘 剑1,郭良斌1,2
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081)
高压圆盘气体轴承中气流速度高、雷诺数大,气膜内边界层的发展形态对主流和轴承承载力的影响不可忽视。在数值计算方法可行性验证的基础上,采用γ-Reθ转捩模型对具有双对称收缩段结构的高压圆盘气体轴承气膜内的流场进行数值求解,分析气膜间隙、供气压力及轴承半径对气膜边界层的影响。结果表明,减小气膜间隙、降低供气压力、增大轴承半径,均可促进气膜边界层的发展;边界层完全发展后,主流被边界层淹没,边界层内的黏性力作用于气流,气流速度下降,使气膜内的压力维持在较高水平,从而提高了气体轴承的承载能力。根据数值计算结果确定了高压圆盘气体轴承实验模型的工作参数。
气体轴承;可压缩边界层;主流区;γ-Reθ转捩模型;气膜;数值计算
传统的静压止推气体轴承采用锐缘供气孔供气,由于在大供气压力下尖锐边缘引起气体流动分离,使轴承内邻近供气孔处出现复杂的波系结构,其中由一系列斜激波所构成的拟激波区造成很大的总压损失,导致轴承承载力有限[1-2]。而基于拉瓦尔喷管工作原理设计的高压圆盘气体轴承的供气口具有双对称收缩段结构,这种结构将轴承入口气流平稳加速至超音速,避免了气流与轴承壁面的流动分离,改善了气膜内部流场,轴承承载力可以随着供气压力的提高而线性增大,解决了轴承承载力受限的问题[3]。
Eleshaky[2]对高供气压力下传统静压止推气体轴承的内部流场进行数值求解,分析了边界层与主流区波系相互作用下的轴承壁面压力分布特征,但没有研究速度边界层发展形态对主流和轴承承载力的影响。而采用双对称收缩段结构的高压圆盘气体轴承中没有产生类似于文献[2]所述复杂波系,气膜内边界层也未受到复杂波系的影响[3],因此,本文拟采用γ-Reθ转捩模型[4-5]对这种高压圆盘气体轴承的内部流场进行数值计算,研究气膜厚度、轴承半径、供气压力对气膜边界层发展特征和形态的影响,分析边界层与主流相互作用下的轴承承载效率问题,从而为高压气体轴承实验模型结构和工作参数的确定提供依据。
1 控制方程及湍流模型
1.1 控制方程
三维可压缩、稳态流动的控制方程在笛卡尔坐标系下表示为:
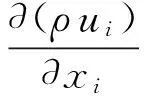
(1)
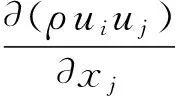
(2)
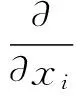
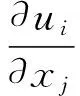
(3)
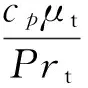
(4)
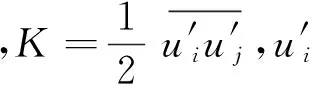
1.2 湍流模型
为使控制方程封闭,需引入湍流模型建立雷诺应力方程组。由于k-ε模型仅适用于充分发展的湍流,无法准确计算存在转捩的流场,而气体轴承收缩段内部流动存在层流向湍流转捩的过程,所以这里选用γ-Reθ转捩模型对轴承内部流场进行计算。
γ-Reθ模型是在SSTk-ω模型基础上引入间歇因子输运方程和动量厚度雷诺数输运方程而建立的,可以准确地模拟层流向湍流发展的过程,并具有预测超声速转捩的能力[6-7]。
间歇因子输运方程:
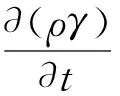
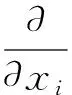
(5)
转捩起始动量厚度雷诺数输运方程:


(6)
用γ修正后的湍动能K输运方程:
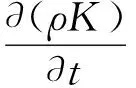
(7)

2 仿真计算
2.1 仿真模型
高压圆盘气体轴承几何模型及计算模型如图1所示,轴承为柱对称结构,所以计算域取其几何模型的1/2。不同算例的模型尺寸如表1所示,表中Ps、Pb分别为轴承的供气压力和出口压力。
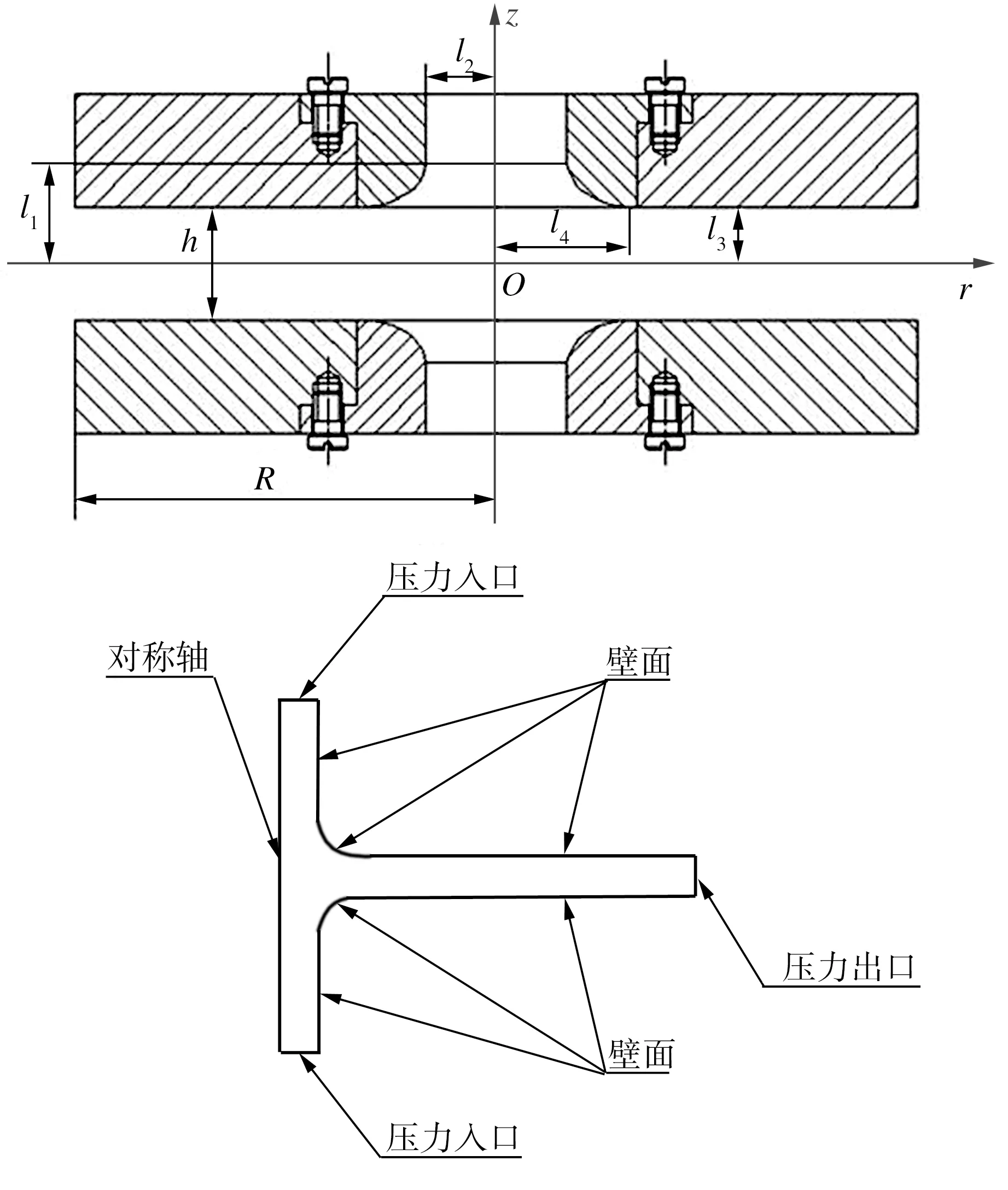
图1 高压圆盘气体轴承模型
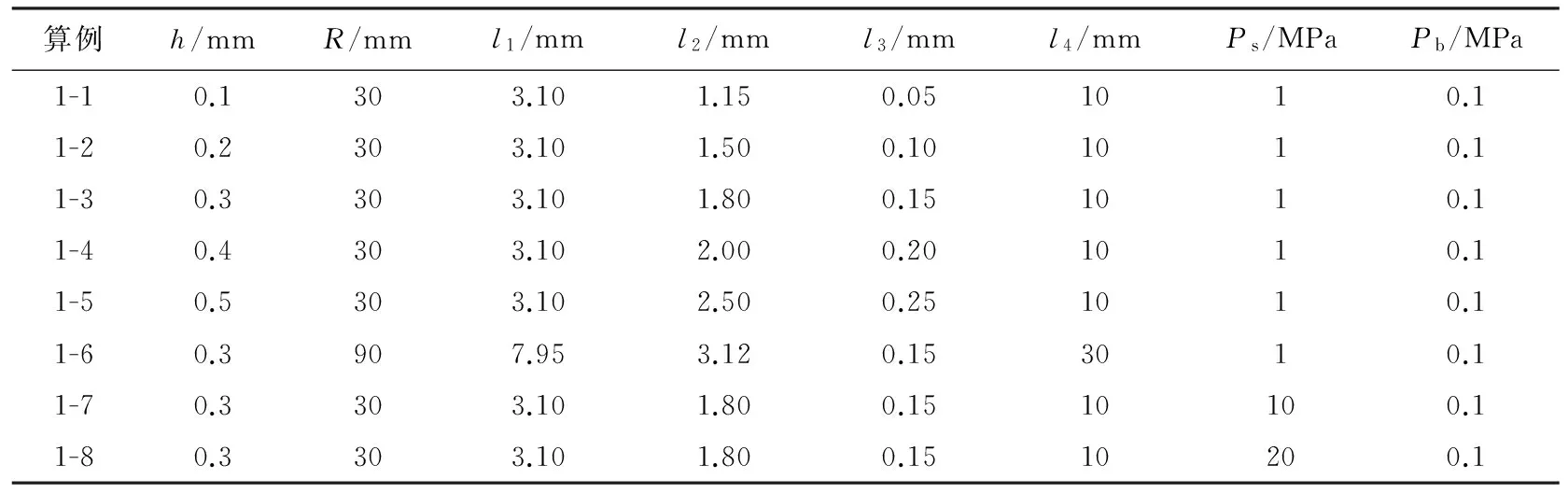
算例h/mmR/mml1/mml2/mml3/mml4/mmPs/MPaPb/MPa1-10.1303.101.150.051010.11-20.2303.101.500.101010.11-30.3303.101.800.151010.11-40.4303.102.000.201010.11-50.5303.102.500.251010.11-60.3907.953.120.153010.11-70.3303.101.800.1510100.11-80.3303.101.800.1510200.1
2.2 计算方法
Fluent中基于密度法的求解器适用于可压缩流体,在马赫数较大时,其收敛性较好,因此本文选用密度基求解器,并采用Roe-FDS计算格式对轴承内部流场进行数值计算。
2.3 网格划分及边界条件
y+为无量纲参数,可以反映近壁面网格质量的好坏[8-9],通过调整轴承壁面第一层网格的高度,将y+值控制在5以内。
气流密度设置为ideal-gas;定压比热容cp及湍流普朗特数Prt视为常量;气膜内气体温度梯度较大,动力黏度采用Sutherland公式计算。
2.4 数值计算方法可行性分析
为了验证本文所用γ-Reθ模型及计算方法的
可靠性,对文献[2]中的静压止推气体轴承模型算例(轴承几何模型见图2,不同算例的模型尺寸见表2)进行数值计算,获取轴承壁面压力分布,并与文献[2]中的实验数据进行对比,结果如图3所示。由图3可见,数值计算得出的压力分布与实验数据吻合较好,这表明采用γ-Reθ模型对气体轴承内部流场进行数值计算是可行的,且计算结果可靠。
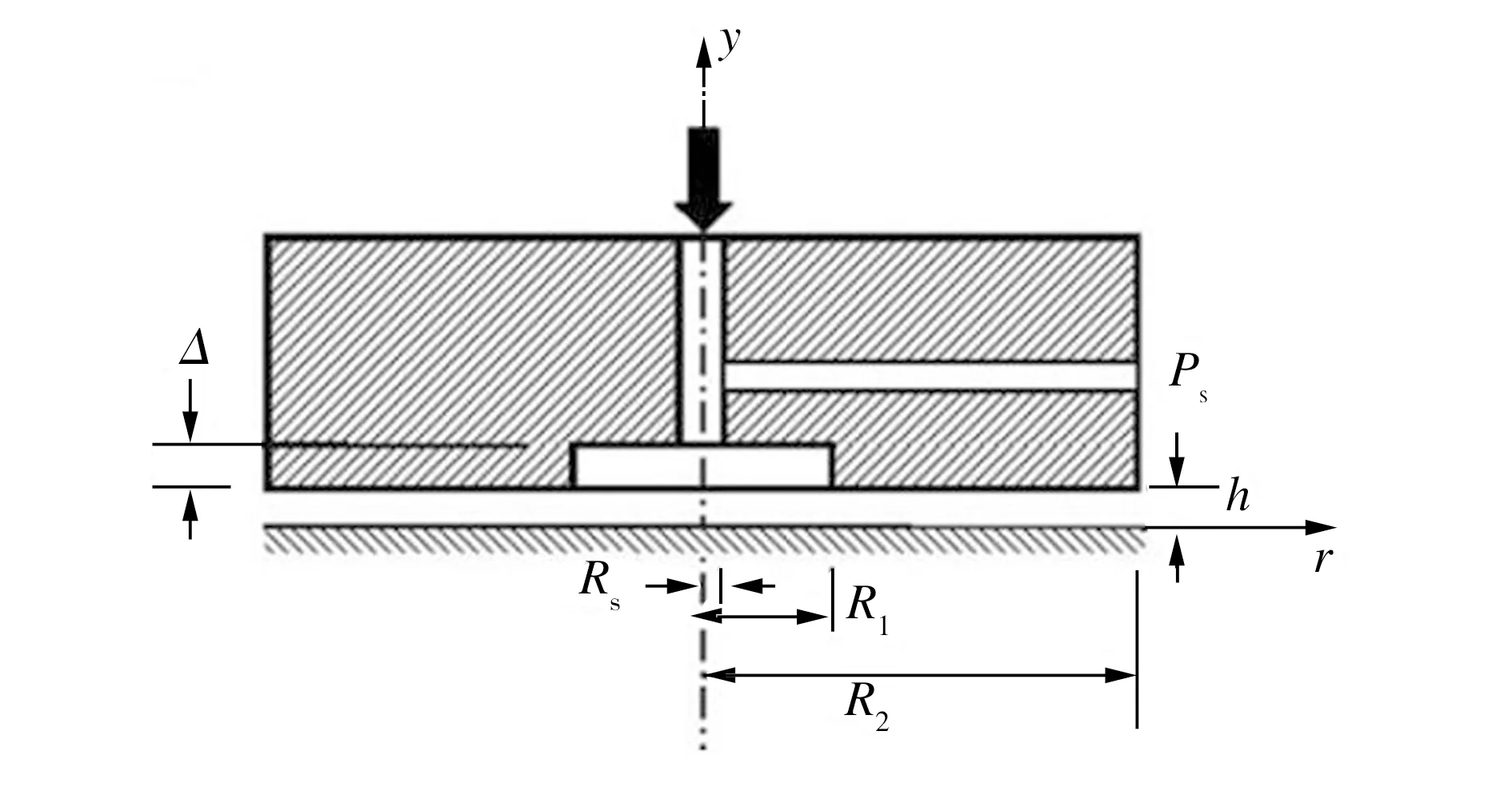
图2 静压止推气体轴承几何模型[2]
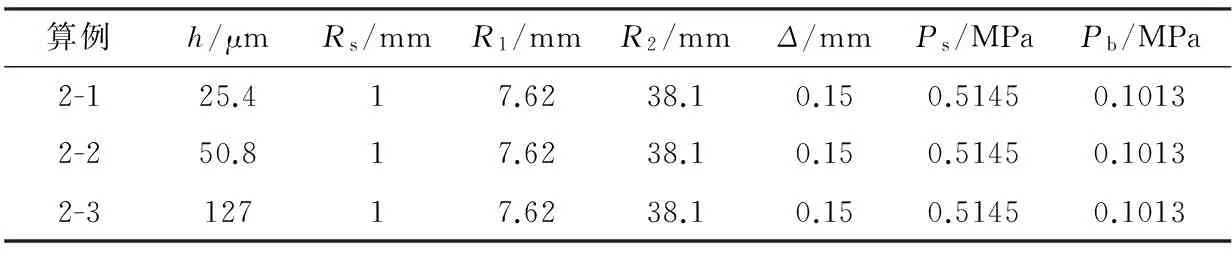
表2 静压止推气体轴承模型尺寸和压力参数[2]
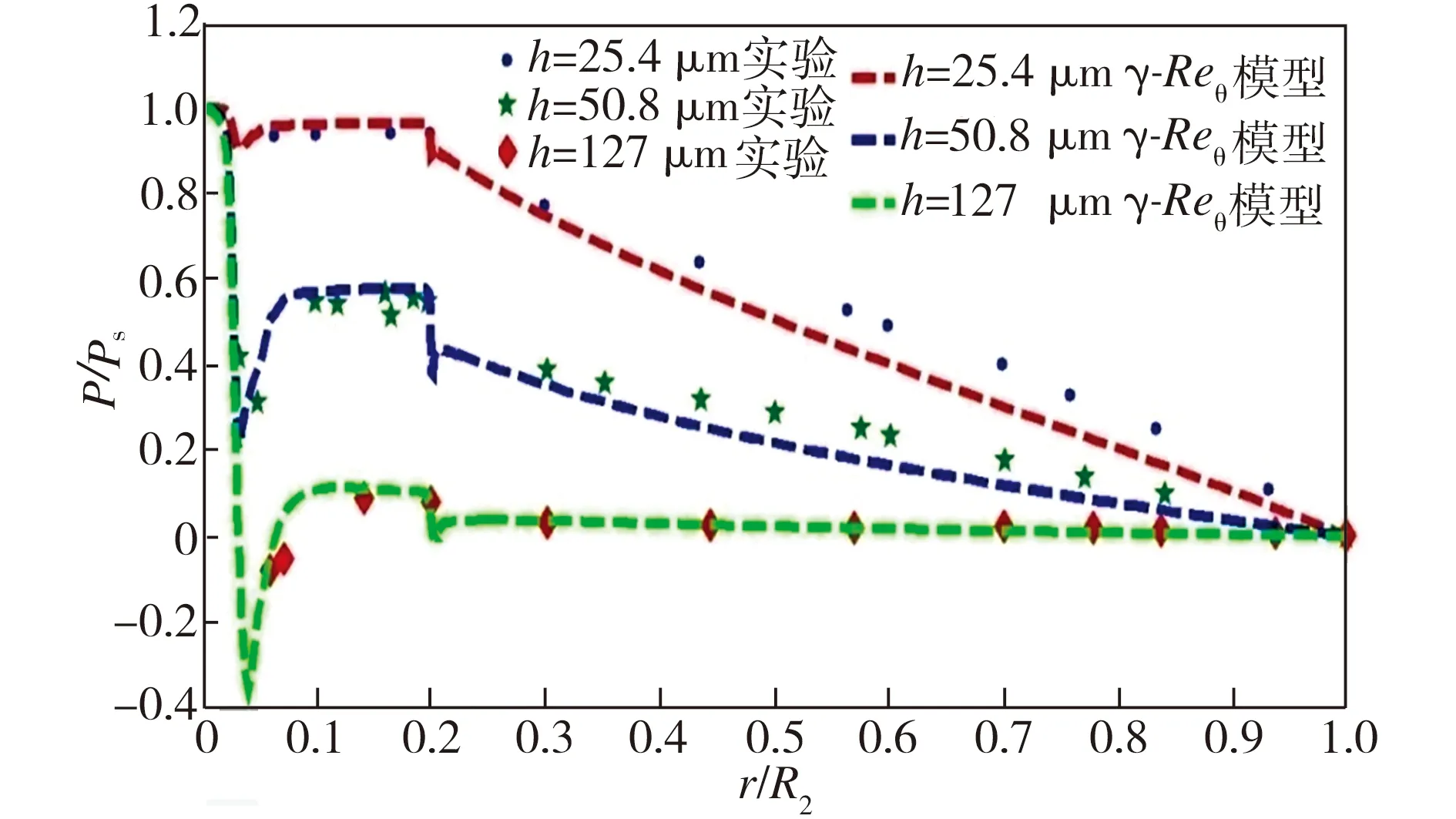
图3采用γ-Reθ模型计算的压力数据与文献[2]中实验数据的对比
Fig.3Pressuredatabyγ-ReθmodelcomparedwithexperimentdatafromRef.[2]
3 仿真结果分析
3.1 气膜间隙对边界层形态的影响
对表1中算例1-1(h=0.1 mm)、1-3(h=0.3 mm)、1-4(h=0.4 mm)、1-5(h=0.5 mm)进行数值计算,得到气膜不同截面上的马赫数分布曲线如图4所示,图中r=10 mm的截面为收缩段出口截面,气流在此截面上的速度均达到临界音速。
由图4可见,在不同气膜间隙下,边界层形态的变化趋势基本一致,即边界层厚度沿气流流动方向逐步增加,而气膜内主流区(曲线中平直部分所示)逐渐变窄。同时,由图4中不同气膜间隙下r=10 mm截面上的马赫数分布曲线可以看出,轴承上、下圆盘壁面附近存在明显的速度梯度,而气膜中心区域的马赫数均匀一致,这表明在r=10 mm的截面上,轴承上、下圆盘壁面处的边界层很薄,主流区很厚。
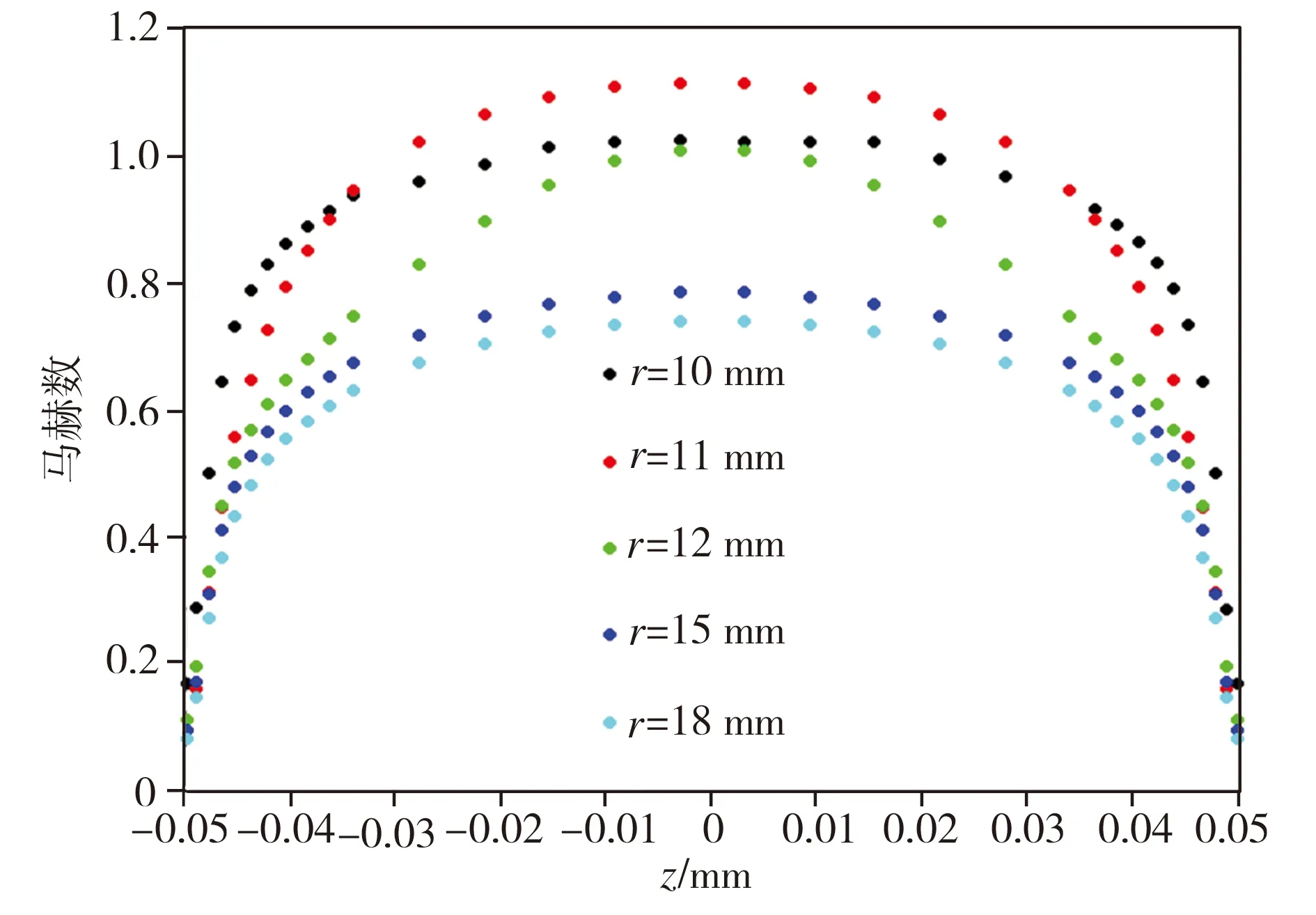
(a)算例1-1(h=0.1 mm)
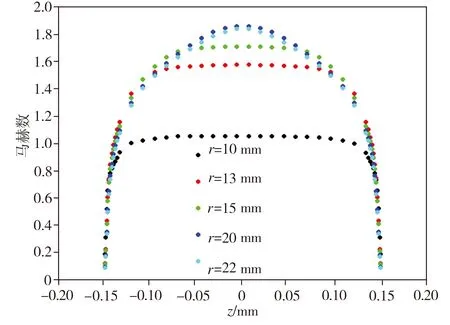
(b) 算例1-3(h=0.3 mm)
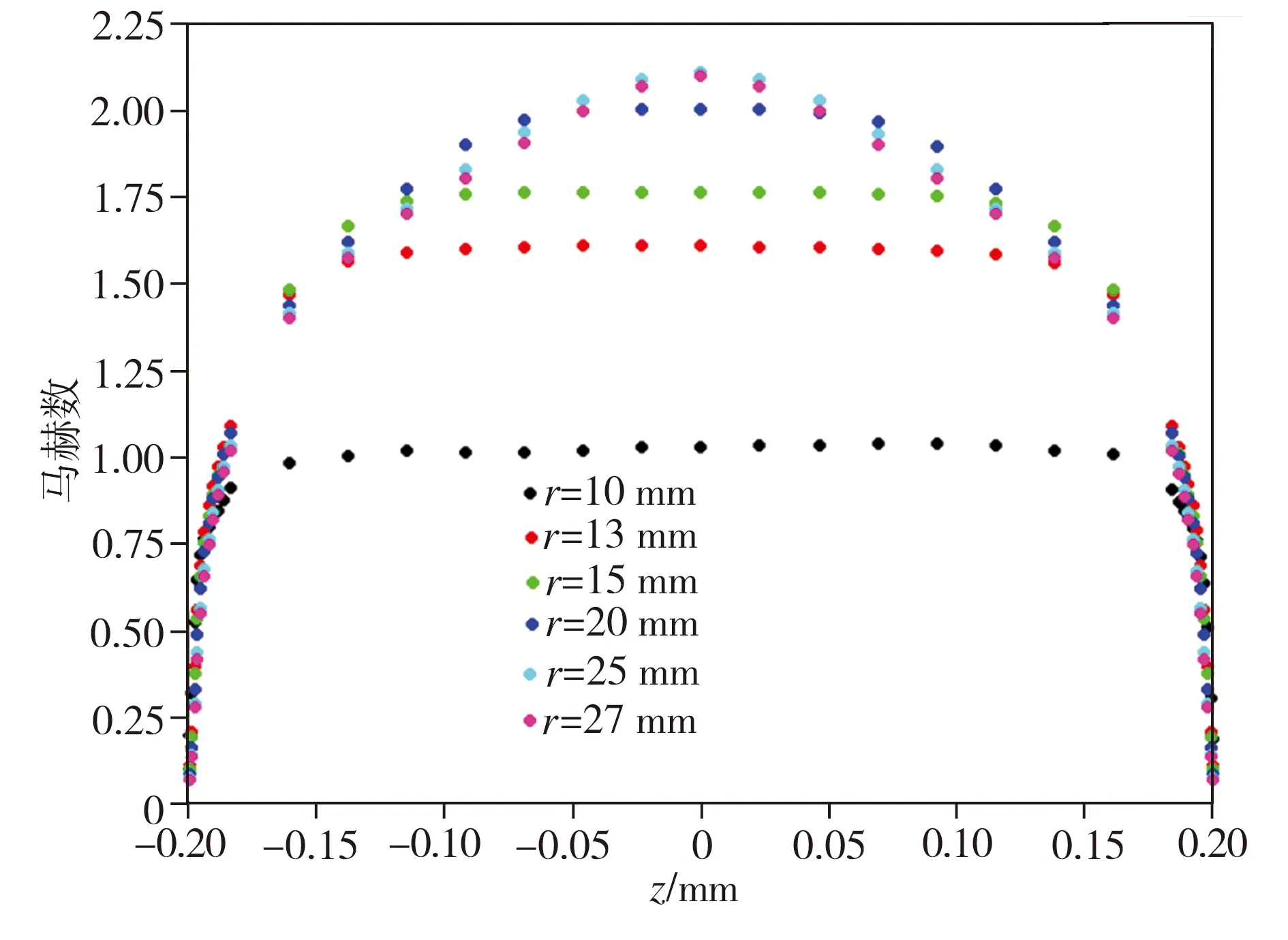
(c)算例1-4(h=0.4 mm)
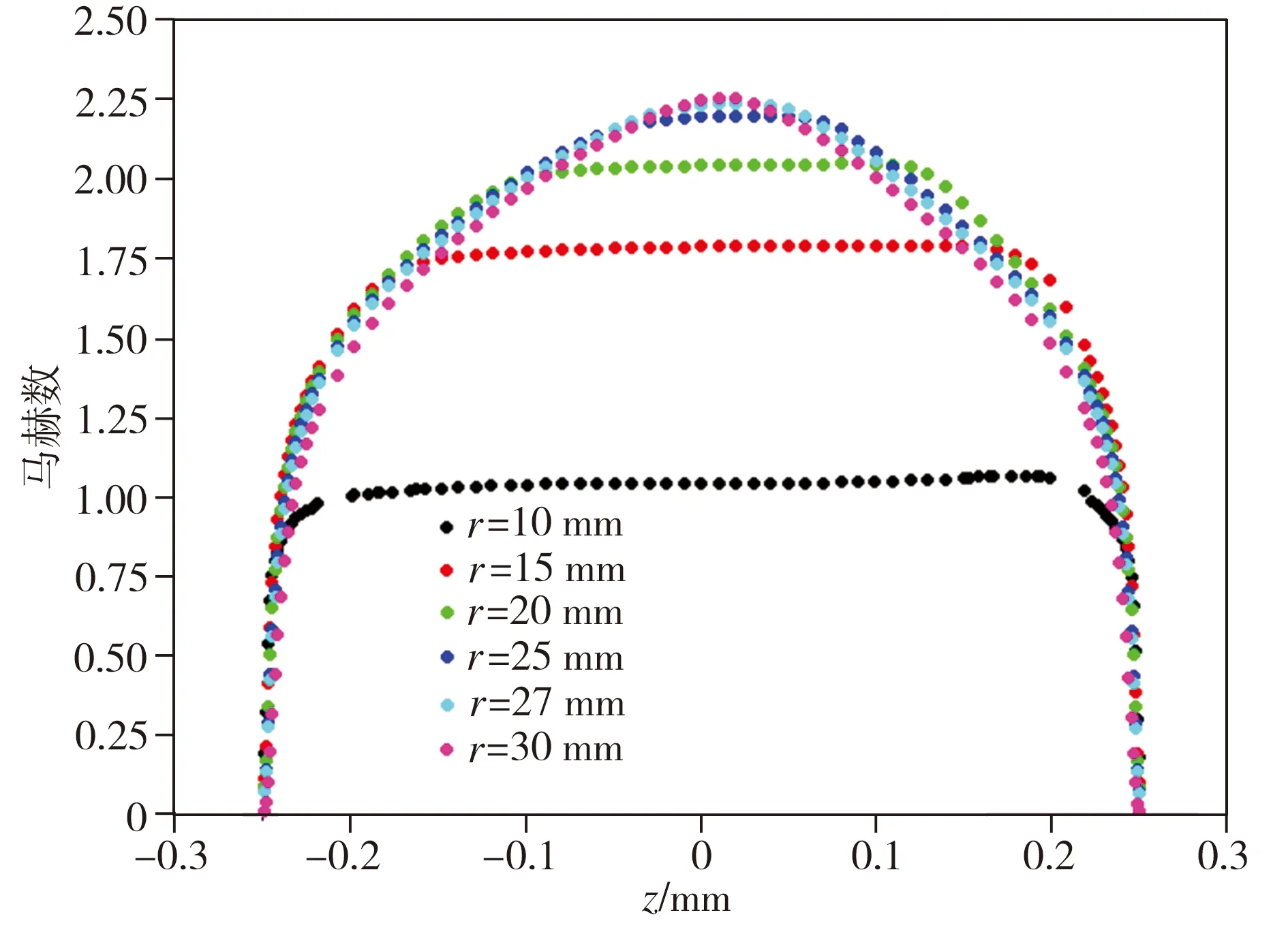
(d)算例1-5(h=0.5 mm)
图4不同气膜间隙下气膜各截面的马赫数分布
Fig.4Mahernumberdistributionindifferentsectionsofgasfilmwithdifferentclearances
在图4(a)中r=11 mm截面、图4(b)中r=20 mm截面、图4(c)中r=25 mm截面上,存在速度梯度的区域扩展至整个气膜区域,上、下圆盘壁面处的边界层交汇,主流区被边界层淹没,边界层完全发展。而图4(d)中气膜间隙较大,上、下圆盘壁面处的边界层在气膜内没有交汇,边界层未能完全发展,主流区依旧存在。这种现象说明:在其它参数不变的情况下,随着气膜间隙的增大,气膜内边界层完全发展的位置向轴承间隙出口方向移动;气膜间隙越小,边界层发展得越快,反之边界层发展越迟缓,当气膜间隙足够大时,边界层在轴承气膜内未能完全发展。
边界层中的黏性力与惯性力处于同一数量级,因此边界层内的黏性力对气流的影响不能忽视。黏性力使气流的动能转化为热能,进而使气流速度下降[10],当轴承圆盘壁面的边界层交汇时,边界层将整个主流区淹没,主流受到边界层内黏性力的影响,减速变为边界层的一部分。
为了进一步说明边界层对主流及轴承承载力的影响,通过数值计算得到算例1-1、1-2、1-3、1-4、1-5中气膜对称面上的马赫数分布及轴承壁面压力分布,分别如图5和图6所示。

图5 不同气膜间隙下气膜对称面上的马赫数分布
Fig.5Mahernumberdistributioninsymmetryplanesofgasfilmswithdifferentclearances
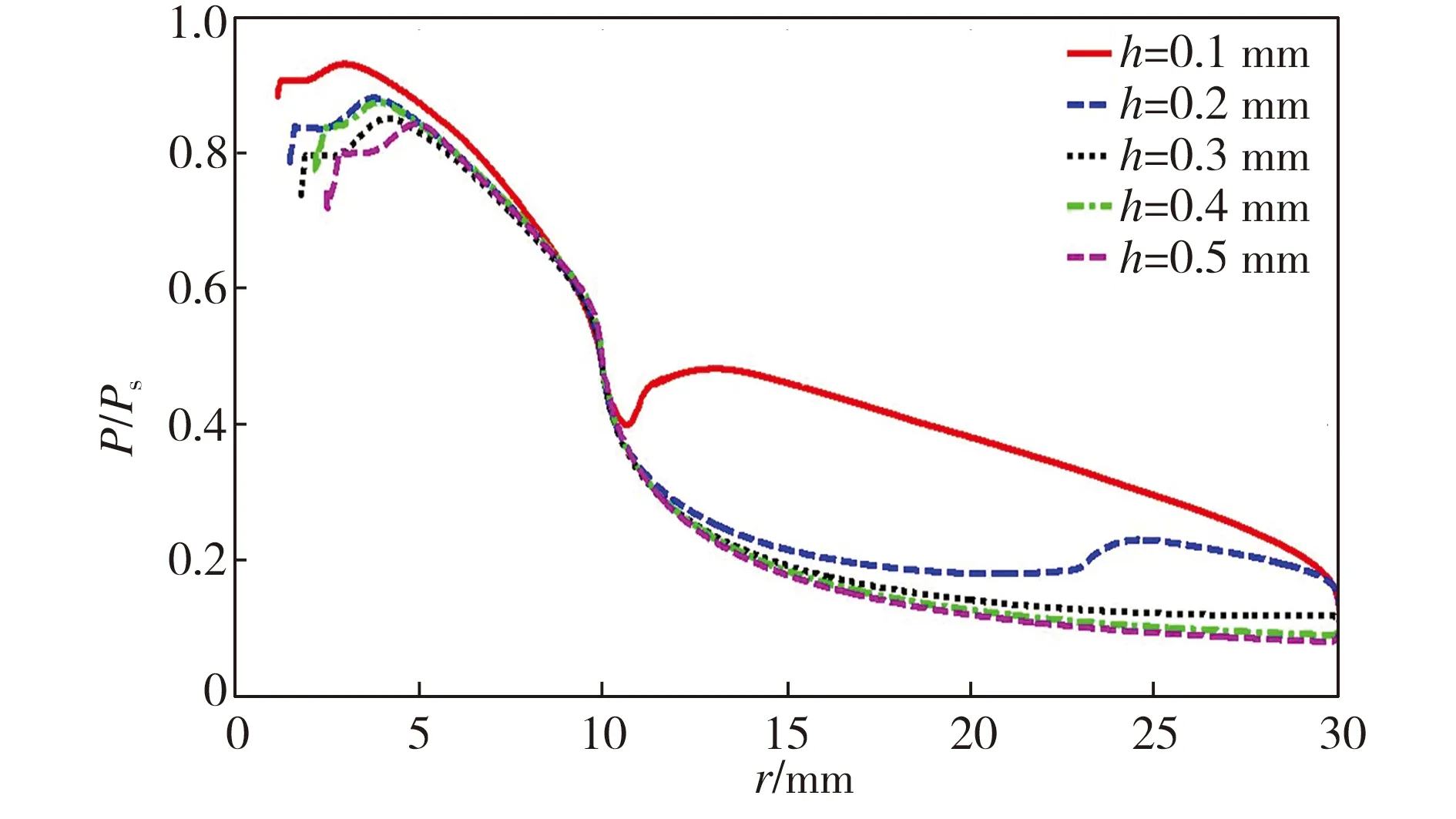
图6 不同气膜间隙下气体轴承壁面压力分布
Fig.6Pressuredistributionongasbearingwallswithdifferentgasfilmclearances
图5中r<10 mm的区域为轴承收缩段,在此区域内,5种气膜间隙下的马赫数变化规律基本相似,即气流均在收缩段区域内加速,并在r=10 mm截面(收缩段出口截面,图中A点)上达到临界音速。
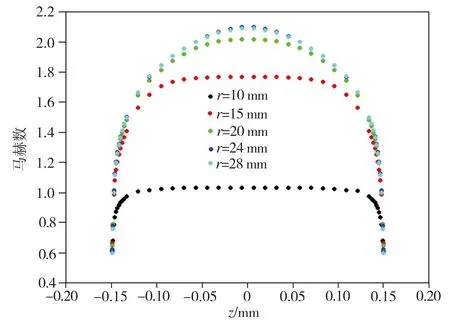
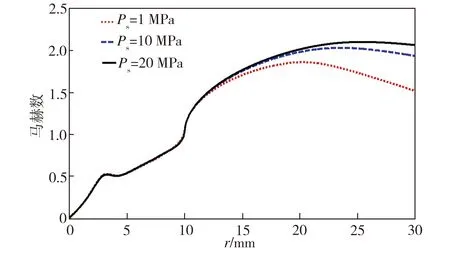
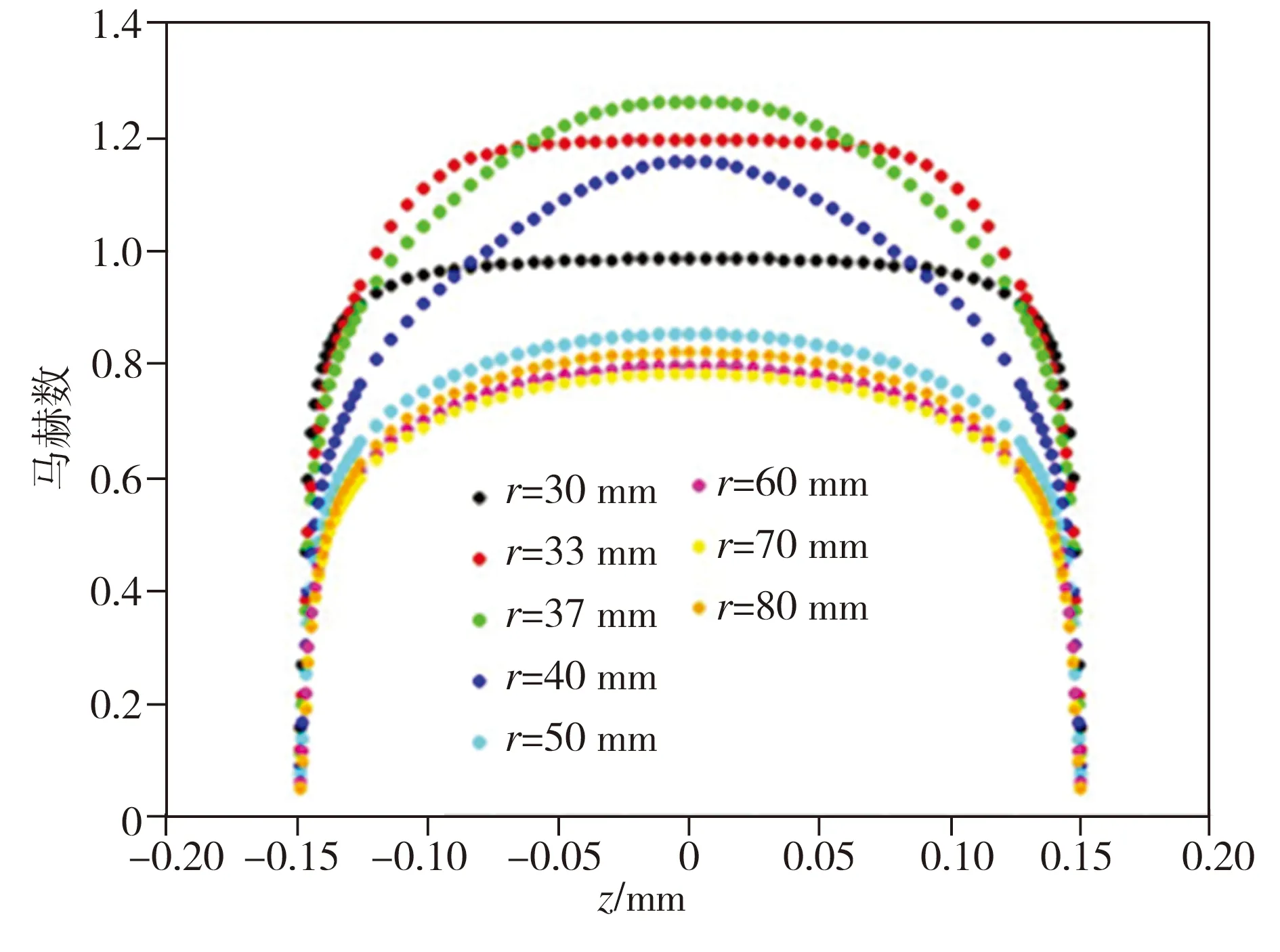
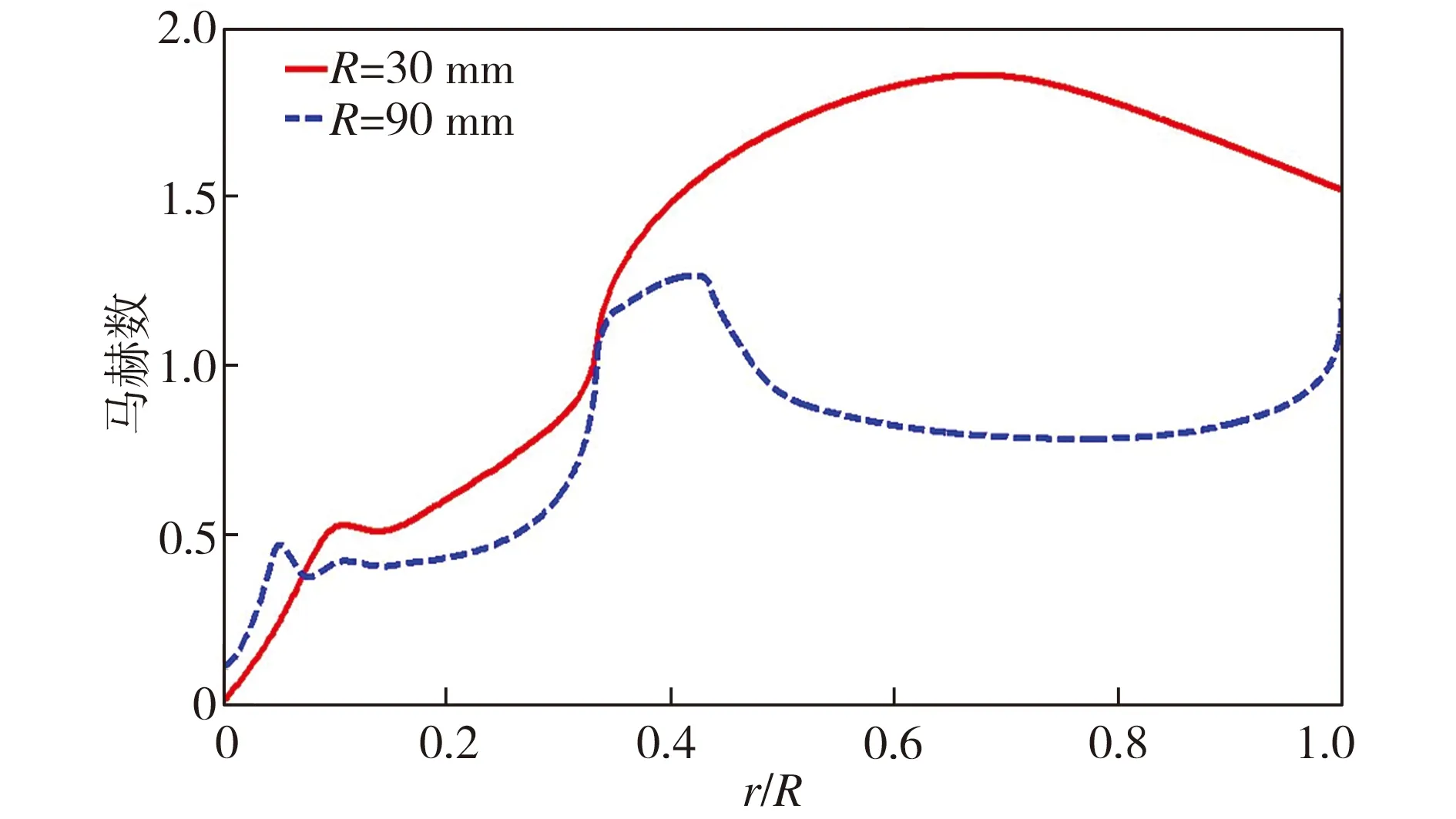
图5中10 mm 图5中B、C、D、E点正是各个轴承模型中气膜内边界层完全发展、主流区被边界层淹没的位置,B、C、D、E点之后气流马赫数下降,这说明边界层的发展是造成气膜内气流速度下降的根本原因之一。而气膜间隙h=0.5 mm的轴承模型中边界层在气膜内未能完全发展,边界层中的黏性力并未对整个主流区气流造成影响,所以其气膜对称面上的气流一直处于加速状态。 从图6可知,随着气膜间隙的增大,轴承壁面压力逐渐减小,因而轴承承载力逐渐下降。其原因在于随着气膜间隙的增大,边界层发展变慢,边界层对主流的影响减弱,所以主流区气流速度增大。气流速度的快速增大必然会造成壁面压力和轴承承载力的下降。 当入口压力Ps=1 MPa时,采用如下公式计算不同气膜间隙下的轴承承载效率: (8) 式中:W为轴承承载力;P1为轴承收缩段区域的壁面压力;P2为轴承气膜区域的壁面压力。 提取数值计算所得压力分布数据,利用MATLAB编程计算不同气膜间隙下的轴承承载效率,结果如表3所示。从表3中可知,减小气膜间隙可提高轴承的承载效率。这是因为,气膜间隙减小可促进边界层的发展,气流受边界层内黏性力的影响,速度下降,进而避免了气膜压力的快速下降,从而提高了轴承的承载效率。所以,在设计高压气体轴承时,在保证轴承间隙出口是超音速的条件下,要尽量减小气膜间隙。 表3不同气膜间隙下的轴承承载效率 Table3Load-carryingefficiencyofgasbearingswithdifferentgasfilmclearances h/mm0.10.20.30.40.5η0.38680.26800.21500.20090.1927 3.2 供气压力对边界层形态的影响 算例1-3、1-7、1-8中供气压力分别为1、10、20 MPa,气膜厚度h(=0.3 mm)及其它参数均一致。对这3个算例进行数值计算,算例1-8中气膜不同截面上的马赫数分布如图7所示,而3个算例在不同供气压力下气膜对称面上的马赫数分布如图8 所示。 图7算例1-8(Ps=20MPa)中气膜不同截面上的马赫数分布 Fig.7MahernumberdistributionindifferentsectionsofgasfilminCase1-8(Ps=20MPa) 图8 不同供气压力下气膜对称面上的马赫数分布 Fig.8Mahernumberdistributioninsymmetryplanesofgasfilmsatdifferentgasinletpressures 从图7可以看出,在供气压力为20 MPa时,边界层在r=24 mm的位置完全发展,而结合图4(b)中算例1-3(h=0.3 mm)的马赫数分布可知,当供气压力为1 MPa时,边界层在r=20 mm的位置完全发展。从图8可以看出,当供气压力分别为1、10、20 MPa时,气膜对称面上的气流马赫数分别在r=20、22、24 mm的位置开始下降。上述结果表明,随着气流入口压力的增大,边界层发展有所变缓,但供气压力对边界层形态的影响并不是太明显,因此其对气体轴承承载效率的影响也较小。 3.3 轴承半径对边界层形态的影响 算例1-3、1-6中供气压力和气膜厚度相同,但轴承半径不同,分别为30、90 mm,相应的供气口收缩段结构尺寸不同。算例1-6中气膜不同截面上的马赫数分布如图9所示,而两个算例在不同轴承半径下气膜对称面上的马赫数分布如图10所示。 结合图4(b)、图9和图10可以看出:算例1-3中,收缩段出口半径r=10 mm,边界层在r=20 mm的位置完全发展(如图4(b)所示),气膜对称面上的马赫数在r/R=0.67的位置开始下降(图10中R=30 mm的曲线所示);算例1-6中,收缩段出口半径r=30 mm,边界层在r=37 mm的位置完全发展(如图9所示),气膜对称面上的马赫数在r/R=0.41的位置开始明显下降(图10中R=90 mm的曲线所示)。这表明轴承半径的增大促进了边界层的发展。 图9 算例1-6(R=90mm)气膜不同截面上的马赫数分布 Fig.9MahernumberdistributionindifferentsectionsofgasfilminCase1-6(R=90mm) 图10 不同轴承半径下气膜对称面上的马赫数分布 Fig.10Mahernumberdistributioninsymmetryplanesofgasfilmsatdifferentbearingradii 边界层形态的变化会造成气膜内速度分布的改变,算例1-3中,气膜内气流速度虽有所下降,但仍处于超音速;而算例1-6中,气膜内气流速度下降至亚音速,亚音速气流比超音速气流的壁面压力高,因此算例1-6中的轴承承载效率要比算例1-3的高。 3.4 高压圆盘气体轴承实验模型的优选 当气体轴承气膜内的气流速度处于亚音速时,其承载效率较高,所以期望轴承收缩段出口之后的气流能减速至亚音速。同时,为了避免环境低压对轴承内部流场的不利影响,并结合超音速气流具有下游低压扰动不会对上游压力分布造成影响的特点,所以期望轴承出口的气流速度能加速到超音速。因此,在所给的8个高压圆盘气体轴承模型中,满足上述要求的有算例1-1(R=30 mm,h=0.1 mm)和算例1-6(R=90 mm,h=0.3 mm)。这两个实验模型中气膜内气流速度受到边界层内黏性力的作用,均处于亚音速,轴承承载效率较高,同时轴承间隙出口处气流均为超音速,避免了环境低压对气膜内压力分布的不利影响。 (1)对于采用双对称收缩段结构的高压圆盘气体轴承,减小气膜间隙、降低供气压力、增大轴承半径,均可促进边界层的发展,其中气膜间隙对边界层形态的影响最为显著。 (2)随着边界层的发展,边界层厚度增加,主流区变窄。当边界层完全发展后,主流区消失,同时边界层内的黏性力作用于气流,气流速度下降,使气膜内压力维持在较高水平,从而提高了气体轴承的承载效率。 (3)根据边界层与主流相互作用改变气流压力分布的特点,初步确定实验轴承模型参数如下:当R=30 mm时,气膜厚度选择h=0.1 mm,即算例1-1;当R=90 mm时,气膜厚度选择h=0.3 mm,即算例1-6。 [1] 王祖温,孙昂.静压气体轴承超声速现象的研究与发展[J].机械工程学报,2006,42(1):6-10. [2] Eleshaky M E. CFD investigation of pressure depressions in aerostatic circular thrust bearings [J]. Tribology International, 2009, 42: 1108-1117. [3] 徐凡.高供气压圆盘止推轴承设计理论研究及实验[D].武汉:武汉科技大学,2016. [4] Menter F R, Langtry R B, Likki S R, et al. A correlation-based transition model using local variables—Part 1: model formulation[J]. Journal of Turbomachinery, 2006,128(3):413-422. [5] Langtry R B, Menter F R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes[J]. AIAA Journal, 2009,47(12):2894-2906. [6] 王刚,刘毅,王光秋,等.采用γ-Reθ t模型的转捩流动计算分析[J].航空学报,2014,35(1):70-79. [7] 孔维萱,阎超,赵瑞.γ-Reθ模式应用于高速边界层转捩的研究[J].空气动力学学报,2013,31(1):120-126. [8] 王明华,陈劲松.发动机喷管内流场对流换热系数影响因素的数值分析[J].火箭推进,2011,37(3):32-37. [9] 覃文洁,胡春光,郭良平,等.近壁面网格尺寸对湍流计算的影响[J].北京理工大学学报,2006,26(5):388-392. [10] 贾忠湖.飞行原理基础[M].北京:国防工业出版社,2016:14-15. [责任编辑尚晶] Analysisofcompressibleboundarylayerpatternofhighpressurecirculargasbearing LiuJian1,GuoLiangbin1,2 (1.Key Laboratory of Metallurgical Equipment and Control Technology of Ministry of Education, Wuhan University of Science and Technology, Wuhan 430081, China; 2. Hubei Key Laboratory of Mechanical Transmission and Manufacturing Engineering, Wuhan University of Science and Technology, Wuhan 430081, China) In the high pressure circular gas bearing, airflow velocity is high and Reynolds number is large, so the impact of development pattern of boundary layer in the gas film on the mainstream and bearing’s load carrying capacity cannot be ignored. Based on the feasibility of numerical calculation method, which was validated,γ-Reθtransition model was used to numerically solve the flow field in the gas film of high pressure circular gas bearing with disymmetric contraction cone, then the influences of gas film clearance, gas inlet pressure and bearing radius on the boundary layer of gas film were analyzed. The results show that decreasing gas film clearance and gas inlet pressure as well as increasing bearing radius can promote the development of gas film boundary layer; the mainstream is submerged by the boundary layer which has been fully developed, and the viscous force in the boundary layer acts on the airflow, causing the decline in airflow velocity and keeping the pressure in the gas film at a high level, thereby the load carrying capacity of the gas bearing is improved. According to the numerical calculation results, the working parameters of experimental model of high pressure circular gas bearing are determined. gas bearing; compressible boundary layer; mainstream zone;γ-Reθtransition model; gas film; numerical calculation TH133.35;V211.3 A 1674-3644(2017)06-0439-07 2017-06-26 国家自然科学基金资助项目(51475341). 刘 剑(1985-),男,武汉科技大学硕士生.E-mail:liujian09@qq.com 通讯简介:郭良斌(1973-),男,武汉科技大学教授,博士.E-mail:guoliangbin@sina.com 10.3969/j.issn.1674-3644.2017.06.007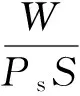

4 结论

