红外光激励的CNF复合微悬臂梁稳态响应特性

林 成

(内江师范学院 物理与电子信息工程学院，四川 内江 641199)

红外光激励的CNF复合微悬臂梁稳态响应特性

林 成

(内江师范学院 物理与电子信息工程学院，四川 内江 641199)

研究了红外光源激励下，以碳纳米管薄膜为吸光层的复合结构微悬臂梁的光热响应特性﹒建立了温度分布理论模型和光热挠曲理论模型，进而得到其一维温度分布与激光照射位置的关系﹒由光热挠曲模型，对碳纳米管薄膜的厚度进行了优化设计，最后计算得到微悬臂梁的挠曲量随激光功率线性增加，结果表明以碳纳米管薄膜作为吸光层的复合结构微悬臂梁使光热探测灵敏度提高了1.2倍﹒研究结果表明，该类碳纳米管薄膜为吸光层的复合结构微悬臂梁作为高灵敏度光热传感器的可能性﹒

光热响应；微悬臂梁；碳纳米管薄膜；红外光源

作为一种重要的微机电系统结构，由于能够实现10-5K温度变化、20 fJ能量变化以及10 pW功率变化探测[1-3]，复合结构微悬臂梁广泛应用于光热传感器和驱动器﹒复合结构微悬臂梁一般由Si或者SiNx悬臂梁和其表面沉积的一层热膨胀系数较大的金属膜构成﹒微悬臂梁吸收光能后温度升高，材料热膨胀系数不匹配所产生的内部热应力使微悬臂梁发生挠曲或振动，从而实现红外激励光的探测﹒通过对微悬臂梁对红外光源的响应特性分析和研究实现其优化设计，可以有效的提高其探测灵敏度和应用范围﹒

微悬臂梁的红外探测灵敏度主要受限于其红外吸光效率和光热转换效率﹒碳纳米管(Carbon nanotube, CNT)作为一种新型纳米材料，具有优异的光学、热学、电学和机械特性，光热转化效率极高[4]﹒尽管碳纳米管阵列显示出近似黑体效应，其红外吸光效率高达 90%以上[5]，但是其制备工艺和过程复杂﹒相反，无序碳纳米管薄膜(Carbon nanotube film, CNF)的制备相当简单，而且具有极高的红外光和热辐射源吸收效率[6-7]﹒本文结合纳米技术，选择碳纳米管薄膜作为红外光吸收材料，从而极大地提高了红外探测灵敏度﹒

首先基于COMSOL 5.0 分析软件，对CNF-复合结构微悬臂梁的温度分布进行了仿真计算，建立微悬臂梁稳态温度分布一维物理模型，得到沿长度方向温度分布规律；基于材料力学热力学理论，建立了微悬臂梁挠曲物理模型，得到其挠度与激光参数的关系，进一步对碳纳米管薄膜的厚度进行了优化设计，最后比较了碳纳米管薄膜修饰的微悬臂梁与传统微悬臂梁的探测灵敏度﹒

1 理论模型

如图1所示为CNF复合微悬臂梁的结构和微悬臂梁热流分析示意图，其长、宽和厚度分别为l、w和t，由厚度分别为t1、t2和t3的碳纳米管薄膜、Si基底以及金属镀膜 Al膜构成，红外激光照射范围为l1到l1+2R，其中R为微悬臂梁表面光斑半径﹒红外光源照射到CNF表面，分子动能增加，碳纳米管内部温度增加并快速将热能传递到Si和Al层﹒构成各层材料的热膨胀系数差异较大，不同的热膨胀量在层间产生内部热应力，微悬臂梁发生挠曲﹒

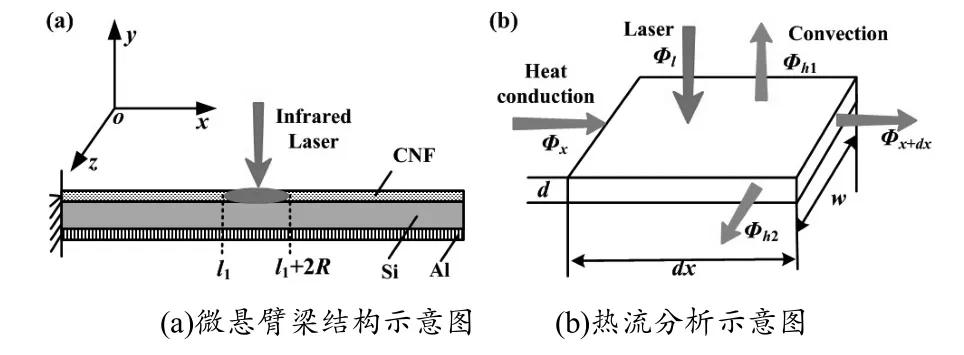
图1 CNF复合微悬臂梁模型

假设微悬臂梁的长宽和厚度分别为800 μm、200 μm 和 8.5 μm，CNF、Si和 Al层的厚度分别为2 μm、5 μm和1.5 μm﹒微悬臂梁左端为固定端，端面温度与空气温度相同且保持不变；右端为自由端，端面与空气之间产生对流换热﹒理论分析中各层材料的物理参数如表1所示﹒温度增量较小时，根据Nusselt Number、Prandtl Number和Grashof Number[8]计算得到微悬臂梁与空气之间的热对流系数为 350 W·m-2·K-1﹒

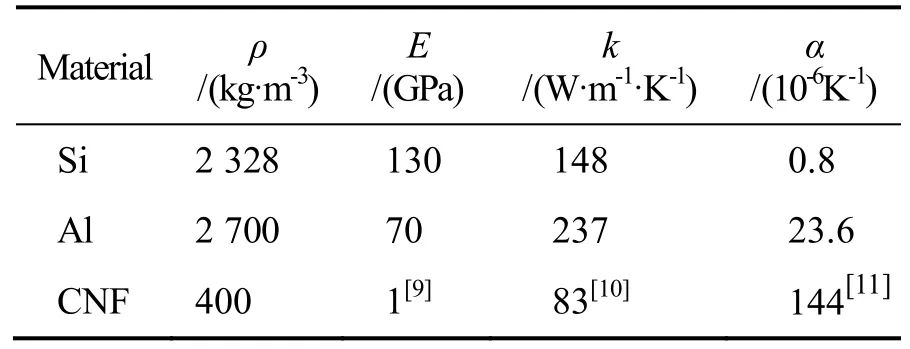
表1 理论分析中各层材料的物理参数

结合图1所示的微悬臂梁结构和表1中的材料参数，假设照射到微悬臂梁表面的激光光斑半径R=100 μm，激光功率P=8 mW，激光照射位置l1=0.2 mm，微悬臂梁吸光率为0.85，初始温度为20℃，利用有限元计算软件 COMSOL得到微悬臂梁的温度分布如图2所示，其中大图为长度方向的温度分布，插图(a)和(b)表示灰色圆点(长度方向温度最大值所对应的位置)处宽度方向和厚度方向的温度﹒从图中可以看到，长度方向温度最大为29.16 ℃，对应位置距离固定端377 μm；灰色圆点处宽度方向的最高和最低温度约为29.16 ℃和28.98 ℃，温差约为初始温度的0.9%；圆点处微悬臂梁下表面到上表面沿厚度方向的温度逐渐增加，其最高和最低温度约为29.16 ℃和29.13 ℃，温差约为初始温度的0.15%﹒因此沿宽度和厚度方向的温度变化可忽略不计﹒

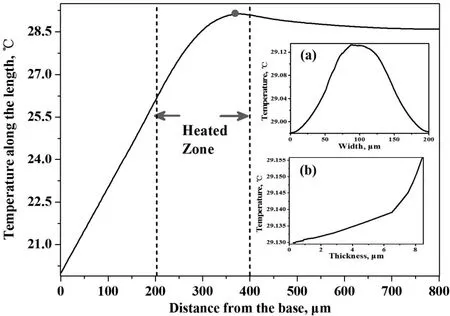
图2 微悬臂梁温度分布

采用上述参数，可以计算得到毕渥数(Biot number)[12]，Bi= 1.0402×10-5(lt;lt;1)，因此可以忽略厚度方向的温度变化；研究证明，当照射到微悬臂梁表面的激光光斑直径与其宽度相当时，其宽度方向的温度分布可以忽略不计[13]，因此结合COMSOL结果，可以将该复合结构微悬臂梁的三维温度分布简化为一维方程﹒根据能量守恒，由图1(b)可以得到微悬臂梁稳态温度微分方程为

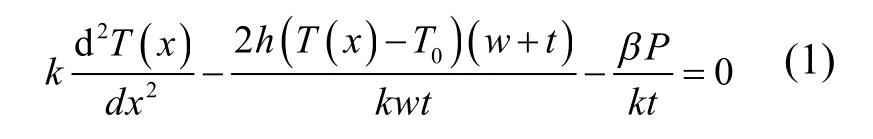
其中k和h分别为微悬臂梁的热导率和换热系数，β为CNF的吸光率，P为激光功率﹒其边界条件可以表示为

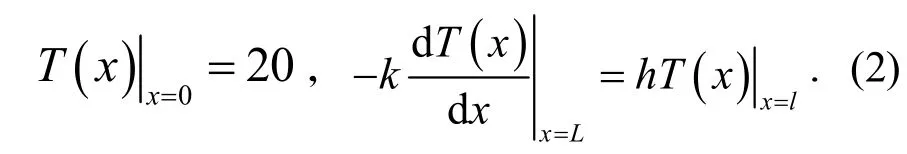
由于构成微悬臂梁各层材料之间的热膨胀系数不同，温度升高所产生的内部热应力使微悬臂梁发生挠曲﹒根据材料力学热力学理论[14]可以得到微悬臂梁挠曲度与温度分布之间的关系

其中，Ei、αi和ti(i=1, 2, 3)分别表示 CNF、Si和Al膜的弹性模量、热膨胀系数和厚度﹒其边界条件可以表示为

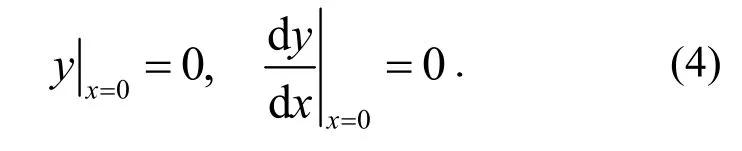
2 结果与分析

采用COMSOL仿真中的参数，根据式(1)-式(2)得到沿长度方向微悬臂梁的温度分布见图 3﹒从图中可以看到，长度方向微悬臂梁的温度先增加后减小，且最高温度位置偏离激光光斑中心，主要是因为微悬臂梁固定端与外界温度一致，端面与空气之间的表面对流换热系数远大于自由端端面与空气之间的对流换热系数﹒通过计算可以得到，微悬臂梁最高温度为29.4 ℃，对应的位置距离固定端385 μm；自由端的温度为28.95 ℃﹒从图中可以看出计算结果与 COMSOL仿真结果变化趋势相同且存在一定偏差，主要是因为由式(1)-式(2)得到的结果是把 COMSOL三维仿真得到的数值解简化到一维引起的﹒

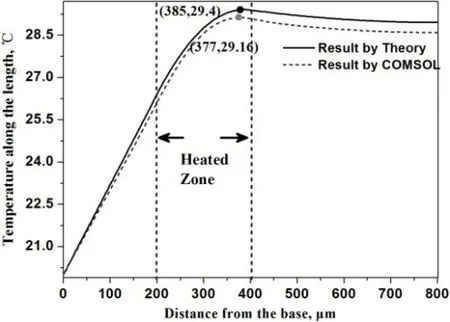
图3 沿长度方向微悬臂梁温度分布

改变激光照射位置，由式(1)-式(2)可以得到微悬臂梁最高温度随激光照射位置的变化曲线如图4所示﹒由图可知，随着激光光斑位置从固定端(x=0)移动到自由端(x=600)，微悬臂梁的温度先增大后减小﹒这主要是因为微悬臂梁固定端可以近似为散热器，对流换热系数接近无限大，而自由端的对流换热系数为有限值﹒因此激光光斑位置距离固定端越远，对流换热所损失的热量越小；但是光斑位置越靠近自由端，通过自由端对流换热所损失的热量也增加﹒

从图4可看出，微悬臂梁自由端挠曲随激光功率的增加而线性增加，因此CNF复合微悬臂梁可以在激光光热光谱痕量物质探测系统中作为光热传感器或是微光热驱动系统中作为驱动器件﹒挠曲-激光功率曲线的斜率反映了微悬臂梁的探测灵敏度，从图中可以看出CNF修饰的3层复合结构微悬臂梁比两层结构微悬臂梁的灵敏度提高了1.2倍﹒

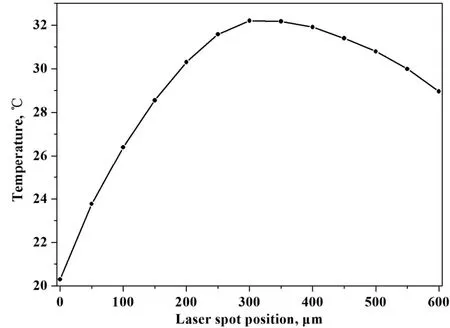
图4 微悬臂梁最高温度随激光照射位置的关系曲线

由于构成微悬臂梁各层材料之间的热膨胀系数不同，温度升高所产生的内部热应力使之发生挠曲﹒激光照射位置l1=0.385 mm时，根据式(3)和(4)计算得到 CNF修饰的复合结构微悬臂梁以及无 CNF修饰的微悬臂梁自由端挠曲随激光功率变化如图5所示﹒

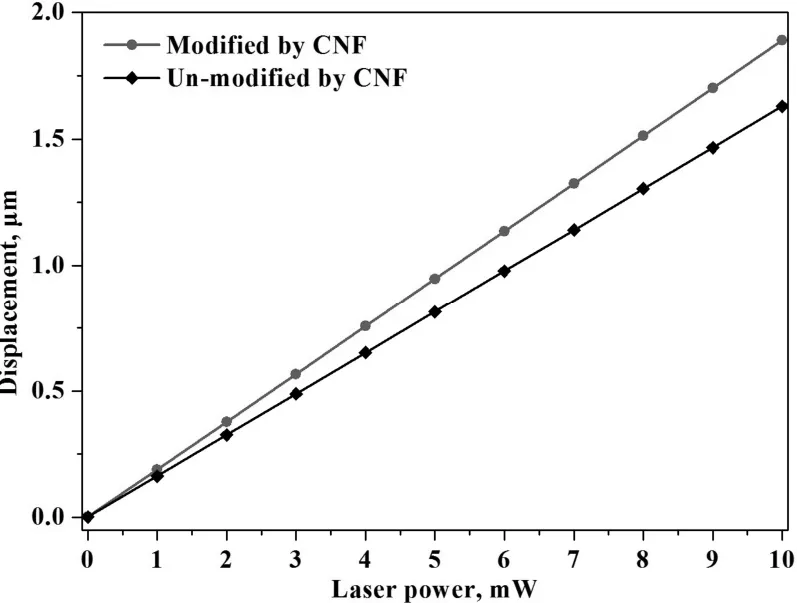
图5 复合结构微悬臂梁挠曲对比曲线

定义微悬臂梁的光强灵敏度为单位激光功率作用下自由端产生的挠曲，由式(3)和式(4)计算得到不同CNF厚度时，微悬臂梁光强灵敏度随Al-Si厚度比的关系曲线如图6所示﹒

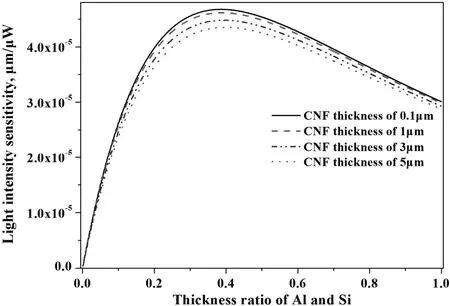
图6 光强灵敏度随Al-Si厚度比变化曲线

从图6可看出，CNF厚度越小其光强灵敏度越大，但是CNF厚度越小其制备越困难且吸光效率越低，而且典型CNF厚度为2 μm[15]，因此在后续实验中的CNF厚度为2 μm，且光强灵敏度最大所是对应的Al-Si厚度比约为0.38，结合微机械加工工艺，在后续实验中优选Si基底、Al膜以及CNF厚度分别为5 μm，1.5 μm和2 μm﹒

3 结论

提出以碳纳米管薄膜作为吸光层的复合结构微悬臂梁﹒采用有限元分析软件 COMSOL仿真计算了微悬臂梁的温度分布，由此建立了稳态温度分布一维微分方程和挠曲微分方程﹒计算结果表明：COMSOL仿真和理论计算结果一致；激光光斑靠近微悬臂梁中心(约为300 μm)时其温度达到最大值；微悬臂梁挠曲随激光功率线性变化，CNF修饰的三层复合结构微悬臂梁的光强探测灵敏度比双层结构微悬臂梁提高了 1.2倍；微悬臂梁光强灵敏度最大时所对应的 Al-Si厚度比为0.38，CNF的最优厚度为2 μm，由此确定后续实验中各层材料的厚度(即 CNF、Al、Si的厚度分别为 2 μm、1.5 μm 和 5 μm)．

[1]Sadat S, Chua Y J and Lee W. Room temperature picowatt-resolution calorimetry[J]. Applied Physics Letters, 2011,99(4): 215502.

[2]Varsi J, Lai J, Perazzo T. Photothermal measurements at picowatt resolution using uncooled micro-optomechanical sensors[J].Applied Physics Letters, 1997, 71(3): 306-308

[3]Perazzo T, Mao M, Kwon O. Infrared vision using uncooled micro-optomechanical camera[J]. Applied Physics Letters, 1999,74(23): 3567-3569.

[4]Ajayan P M, Terrones M, Guardia A de la,et al. Nanotubes in a Flash--Ignition and Reconstruction[J]. Science, 2002, 296(5568):705.

[5]Shi H F, Ok Jong G, Won B H,et al. Low density carbon nanotube forest as an index-matched and near perfect absorption coating[J]. Applied physics letters, 2011, 99(21): 211103.

[6]Gokhale V J, Shenderova O A, McGuire G E,et al. Infrared Absorption Properties of Carbon Nanotube/Nanodiamond Based Thin Film Coatings[J]. Microelectromechanical Systems, 2014,23(1): 191-197.

[7]Kovats E, Pekker A, Pekker S,et al. Carbon Nanotube Films for Optical absorption[J]. Carbon Nanotubes NATO Science Series II:Mathematics, Physics and Chemistry, 2006, 222: 169-170.

[8]John H. Lienhard IV, John H. Lienhard V. A heat transfer textbook[M]. 3rd ed. Phlogiston Press, Cambridge, Massachusetts,2008.

[9]Ajayan P M, Schadler L S, Giannaris C. Single-walled carbon nanotube-polymer composites: strength and weakness[J]. Adv.Mater. 2000, 12(10): 750-753.

[10]Itkis M E, Borondics F, Yu A. Thermal conductivity measurements of semitransparent single-walled carbon nanotube films by a bolometric technique[J]. Nano Letters, 2007, 7(4): 900-904.

[11]Xu Y, Ray G, Abdel-Magid B. Thermal behavior of singlewalled carbon nanotube polymer–matrix composites[J].Composites Part A: Applied Science and Manufacturing, 2006,37(1): 114-121.

[12]Jiji L M. Heat Conduction [M]. New York: Springer-Verlag Berlin and Heidelberg GmbH amp; Co. K, 2009.

[13]Kwon B, Rosenberger M, Bhargava R,et al. Dynamic thermomechanical response of bimaterial microcantilevers to periodic heating by infrared radiation[J]. Review of Scientific Instruments, 2012, 83(1): 015003.

[14]张霞, 焦彬彬, 陈大鹏, 等. 三层材料微悬臂梁模型及其在红外焦平面像元设计中的应用[J]. 红外与毫米波学报, 2010,29(4) : 259-263.

[15]Gong Z C, He Y, Tseng Y H. A micromachined carbon nanotube film cantilever-based energy cell[J]. Nanotechnology,2012, 23 (33): 335401.

(责任编校：蒋冬初)

Response of CNF Composite Micro-cantilever to Infrared Excitation

LIN Cheng
(College of Physics and Electronic Information Engineering, Neijiang Normal University, Neijiang, Sichuan 641199, China)

Photothermal-mechanical response of a composite micro-cantilever modified by carbon nanotube film(CNF) illuminated by an infrared laser source is investigated. The physical model of temperature distribution and photothermal deflection under infrared laser excitation are established. The temperature distribution along the length direction as function of the heat zone is obtained. The thickness of CNF is optimized based on the photothermal deflection model. Last, the deflection of micro-cantilever is calculated and the linear relationship between the deflection and laser power is obtained. The theoretical results show that the photothermal sensitivity of composite micro-cantilever modified by CNF is higher than the usual one, and the sensitivity is increased 1.2 times. The study results demonstrate the feasibility of composite micro-cantilever modified by CNF as photothermal sensor.

photothermal response; micro-cantilever; carbon nanotube film; infrared laser

TH744.1

A

10.3969/j.issn.1672-7304.2017.02.0012

1672–7304(2017)02–0055–04

2017-02-14

四川省教育厅科研项目(16ZA0313)；内江师范学院专利科研项目(15ZL06)

林成(1981-)，男，四川简阳人，讲师，博士，主要从事痕量物质激光光谱检测、微纳米光子学研究，E-mail: lchylinchy@126.com.