宽厚板矫直机工作辊强度分析
赵 岽 吴庆君
(1.太原重工股份有限公司矫直机研究所,山西030024;2.淮南市石油化工机械设备公司技术部,安徽232033)
宽厚板矫直机工作辊强度分析
赵 岽1吴庆君2
(1.太原重工股份有限公司矫直机研究所,山西030024;2.淮南市石油化工机械设备公司技术部,安徽232033)
宽厚板矫直机工作辊承受矫直力大,在设计中必需从轴颈扭转强度、辊身弯曲强度、辊面接触应力三个方面进行强度计算分析。
矫直机;工作辊;扭转强度;弯曲强度;接触应力
宽厚板矫直机所需矫直钢板的尺寸规格大、屈服强度高,工作辊承受矫直力大,为了提高矫直质量应选用较小辊径、辊距参数的工作辊,为了满足矫直精度要求,故在设计中必需对工作辊的强度进行计算分析。
以下以一台9辊宽厚板矫直机工作辊参数为例,在满足对轧件的大变形反弯条件下,即前三辊产生的相对反弯曲率Cw=5时,进料侧第3根工作辊所受矫直力与扭矩值均为各辊中的最大值,依此最大值从轴颈扭转强度、辊身弯曲强度、辊面接触强度三个方面进行工作辊强度校核。
1 宽厚板矫直机的主要技术参数
1.1 矫直机辊系参数
工作辊数n:9
工作辊辊径D/mm:220
工作辊轴颈d/mm:130
工作辊辊距P/mm:260
工作辊身长度L/mm:3600
工作辊材料性能:60CrMoV,调质热处理286~321HBW,屈服极限σs1取640 MPa,许用剪应力[τ]取180 MPa。
支承辊排数n1:6
各排支承辊间距ln/mm:l1=l7=636,l2=l3=l4=l5=l6=550(见图1)
支承辊辊径D1/mm:250
1.2 矫直典型板材规格
矫直板材:合金钢板材
厚度H/mm:20
宽度B/mm:3300
矫直板材屈服极限σs2/MPa:800
2 工作辊轴颈扭转强度
在设定前三辊对轧件的相对反弯曲率Cw=5后,只要给定轧件的断面尺寸与材质性能,就可算出第3辊的矫直力矩T3,故可按轴颈尺寸d与材料的许用剪应力[τ]为条件进行工作辊轴颈扭转强度分析。
2.1 最大单辊矫直力矩
选取典型规格板材的参数,按第3辊的相对反弯曲率Cw=5,计算最大单辊矫直力矩T3为:

=4.269×107N·mm
式中,f为轧件与辊面的滚动摩擦系数,0.2~0.4 mm,取0.4 mm;μ为轴承摩擦系数,0.005~0.01,取0.005;u3为第3辊矫直变形能量比,在相对反弯曲率为5时u3=10;M3为第3辊对板材的相对弯曲力矩,在相对反弯曲率为5时M3=1.48。
板材的弹性变形能μt为:

式中,E为钢质弹性模量,2.1×105N/mm2。
板材的弹性弯矩Mt为:

图1 工作辊对典型板材配置的合成弯矩图Figure 1 Composite bending moment diagram of typical plate configuration to working roll
2.2 扭转强度
按轴颈尺寸计算单辊许用扭转强度MD为:

2.3 计算安全系数
工作辊轴颈扭转强度安全系数K为:

安全系数K=1.75~1.85,在规定范围内。
3 工作辊辊身弯曲强度
对于配置支承辊的工作辊辊身弯曲强度计算,应先按连续梁确定工作辊上各支点的弯曲力矩后再进行。工作辊对典型板材配置的合成弯矩如图1所示,沿工作辊辊身长度上有6个支承辊,可按八支点连续梁进行分段计算求出各支点的弯曲力矩,再根据各支点中的最大弯曲力矩进行弯曲应力校核。
图1中Mi为各支点弯曲力矩;Ri为各支点的支反力;ln为各排支承辊间距。选取典型规格板材的参数,按第3辊相对反弯曲率Cw=5,计算最大单辊矫直力F3为:

假设最大单辊矫直力F3为均布载荷,单位长度的压力q:

3.1 各支点弯曲力矩Mi的计算
连续梁各支点的弯曲力矩计算可采用三弯矩方程式:
Mn-1ln+2Mn(ln+ln+1)+Mn+1ln+1
式中,Mn-1、Mn、Mn+1分别为第n-1、n、n+1支点处的弯矩,单位N·mm;ln、ln+1分别为第n、n+1跨度的长度,单位mm;ωn、ωn+1分别为第n、n+1跨度在外载荷作用下的弯矩图面积,单位N·mm2;an、bn+1分别为弯矩图面积ωn、ωn+1的重心到支点n-1、n+1的距离,单位mm。
3.1.1 0~2段三弯矩方程
0~1段梁上的作用载荷及其弯矩图如图2所示。
计算该段最大弯矩Mmax1为:


图2 0~1段作用载荷及弯矩图Figure 2 Applied loading of 0~1 section and bending moment diagram
式中,A0为只考虑由该段外载荷对支点0产生的支反力;A1′为只考虑由该段外载荷对支点1产生的支反力;a1为弯矩图面积重心到支点0的距离。
计算弯矩图面积ω1为:
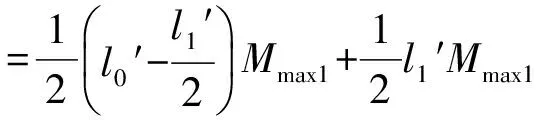
=1.658×1010N·mm2
计算弯矩图面积重心到支点0的距离a1为:
1~2段梁上的作用载荷及其弯矩图如图3所示。

图3 1~2段作用载荷及弯矩图Figure 3 Applied loading of 1~2 section and bending moment diagram
图3中A2′为只考虑由该段外载荷对支点2产生的支反力;A1″为只考虑由该段外载荷对支点1产生的支反力。由于整个跨段作用着均布载荷q,该段最大弯矩Mmax2、弯矩图面积ω2分别为:
Mmax2=1/8ql22=9.184×107N·mm
ω2=2l2Mmax2/3=3.367×1010N·mm2
弯矩图面积重心到支点2的距离b2为:
b2=l2/2=550/2=275 mm
由于支点0的弯曲力矩M0=0,以上数据代入0~2段三弯矩方程整理后得:

3.1.2 1~3段三弯矩方程
由于2~3段的作用载荷及其弯矩图与1~2段(图3)相同,l2=l3=550 mm,ω2=ω3=3.367×1010N·mm2,a2=b3=b2=275 mm,代入以上数据整理后得:

3.1.3 2~4段三弯矩方程
由于3~4段的作用载荷及其弯矩图也与1~2段(图3)相同,l3=l4=550 mm,ω3=ω4=3.367×1010N·mm2,a3=b4=b2=275 mm,M3=M4,代入以上数据整理后得:
3.1.4 弯曲力矩
联合方程式(1)、(2)和(3),求解支点1、2、3处的弯曲力矩:
M1=-0.5×108N·mm
M2=-0.65×108N·mm
M3=-0.61×108N·mm
由于M7=M0,M6=M1,M5=M2,M4=M3,故求出M1,M2,M3后,可得出整个工作辊上各支点的弯曲力矩。
3.2 工作辊辊身弯曲强度计算
由上述计算得出,辊身各支点弯曲力矩最大值在支点2和支点5处且相等,故按M2进行辊身弯曲强度计算。
计算弯曲应力σ为:

计算扭转应力τ为:

按第四强度理论合成σc为:
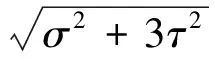

工作辊材料60CrMoV,调质热处理硬度为286~321HBW,屈服极限为σs1,取σs1=640 MPa。工作辊辊身弯曲强度安全系数n=2~2.5。
3.3 辊身弯曲强度计算
对于高强度宽厚板热矫直机来说,所需矫直钢板温度高达450~900℃,故在矫直过程中需对工作辊进行充分有效地冷却,以延长辊子使用寿命,提高板材矫直质量。热矫直机工作辊采用中空通冷却水结构,增加冷却孔直径有利于辊子冷却。
因此,当该工作辊用于热矫直时,按冷却孔内径D1=150 mm进行辊身弯曲强度计算。弯曲应力σr为:


计算扭转应力τr为:

按第四强度理论合成σcr为:
计算安全系数nr为:

4 工作辊辊面接触应力的计算
辊子表面的接触应力σa可用圆柱体与平面相接触时的应力公式计算,辊子上的最大接触应力应小于允许接触应力值[σa],[σa]≈2σs1=1280 MPa,接触应力σa为:

式中,R为矫直辊半径,取110 mm。
计算安全系数s为:

5 结论
综合以上各项分析,工作辊的强度主要受辊面接触应力与轴颈扭转强度的影响;另外,由于工作辊的强度计算受典型板材厚度、宽度、屈服极限的影响,所以依据详细的产品大纲,综合考虑矫直板材的主要规格,选取合理的典型规格板材参数进行计算是非常重要的,并直接影响到分析结果。
编辑 陈秀娟
Strength Analysis of Working Roll of Wide and Heavy Plate Straightener
ZhaoDong,WuQingjun
The working roll of wide and heavy plate straightener is subjected to a great straightening force, the calculation and analysis of intensity shall be performed from three aspects: journal torsion strength, bending strength of roll body and contact stress of roll surface.
straightener; working roll; torsion strength; bending strength; contact stress
2017—04—04
TG333.2+3
B

