超限超载交通对桥梁疲劳损伤及可靠度的影响

赵少杰，任伟新

(1. 中南大学 土木工程学院，湖南 长沙，410075；2. 湖南省交通规划勘察设计院，湖南 长沙，410008；3. 中南公路建设及养护技术湖南省重点实验室，湖南 长沙，410008；4. 合肥工业大学 土木与水利工程学院，安徽 合肥，230009)

超限超载交通对桥梁疲劳损伤及可靠度的影响

赵少杰1,2,3，任伟新1,4

(1. 中南大学 土木工程学院，湖南 长沙，410075；2. 湖南省交通规划勘察设计院，湖南 长沙，410008；3. 中南公路建设及养护技术湖南省重点实验室，湖南 长沙，410008；4. 合肥工业大学 土木与水利工程学院，安徽 合肥，230009)

为了简便、快速地评估交通荷载对桥梁结构疲劳损伤的影响，采用定性分析结合数据拟合的方法建立车辆荷载参数与结构疲劳损伤度之间的量化关系。根据疲劳极限状态方程，考虑到应力与内力的关系，获得疲劳损伤度与疲劳可靠度之间的关系，并进一步建立车辆荷载参数与结构疲劳可靠度之间的量化关系式，为准确、快捷地评估车辆荷载对结构疲劳损伤及可靠度的影响提供一种实用方法。根据该关系式，分析超载超限交通对结构疲劳可靠度的影响。研究结果表明：简支梁结构的疲劳可靠度随着荷载系数K的增大呈对数关系降低；较大的车辆轴距对降低结构的疲劳损伤、提高疲劳可靠度有利。

桥梁工程；疲劳可靠度；统计拟合；疲劳损伤；超载超限交通

桥梁的疲劳荷载及其在疲劳荷载作用下的结构安全可靠度问题一直是工程界研究的热点和难点[1−2]。我国公路桥梁疲劳荷载模型的研究及建立相对滞后，直到2015年才在JTG D64—2015和 JTG D60—2015中明确提出汽车疲劳荷载的标准模型[3−4]，其模型的适用性还需要在实际应用中进一步验证。目前，随着我国交通的不断发展，超载超限车辆越来越多，如何快速、准确地评估桥梁结构在超载超限交通作用下的疲劳安全性是一个有重要应用价值的问题。目前，国内外对超载交通下桥梁疲劳可靠度的研究较少，对疲劳车辆荷载的选取也较随意。一般采用规范标准疲劳车模型[5]或随机选取交通重车作为疲劳荷载[6]进行加载，缺乏对引起疲劳问题的超载超限交通荷载进行系统分析，且对疲劳损伤的计算多基于有限元方法或雨流法等计算手段[7−9]，评估存在随机性，计算过程复杂，不便于工程应用。近年来，随着桥梁健康监测的兴起，一些研究者基于实测车辆动态称重(WIM)数据对桥梁结构的疲劳损伤及寿命进行了评估研究[10−11]，但由于计算过程繁琐，不便于实际工程应用，存在较大局限性。为此，本文作者基于我国典型地区大量车辆动态称重系统的实测交通数据，系统地分析车辆荷载各参数对结构疲劳损伤的影响，并建立各荷载参数与桥梁疲劳损伤及其可靠度之间的量化关系，以便快速、简便地根据实测交通车辆动态称重数据对简支梁结构的疲劳损伤及安全可靠度进行分析评估。

1 各地区车辆荷载数据采集

车辆荷载模型的研究基础是车辆荷载。根据全国各地埋设的动态称重系统(WIM)并结合人工调查，获得了广东、黑龙江、贵州等 6个省份 2013—2015年54万多组车辆WIM数据。通过收集的WIM数据，分析各地区车辆荷载的统计分布特征，如车型比例、轴重力、轴距及车辆间距(简称车距)分布等，为后续疲劳损伤及可靠度的分析提供数据基础。通过统计分析获得的各地区车辆荷载主要特征见表 1，其中湖南省样本中未统计小轿车。

从表1可见：各省份地区汽车荷载均存在超载现象，其中贵州、湖南和湖北的超载程度较大。

2 结构的相对疲劳损伤

由疲劳累积损伤模型，结构的疲劳性能可用S−N曲线描述，其曲线方程为

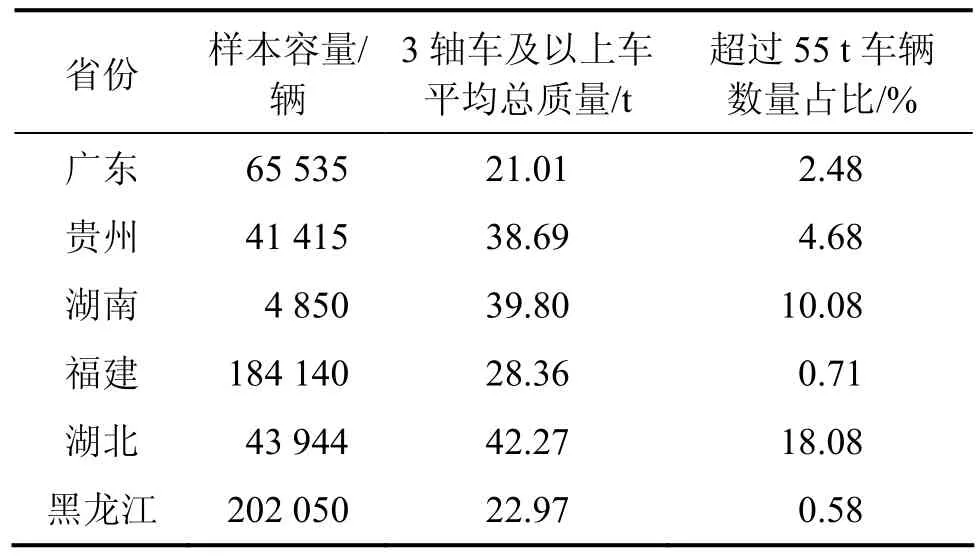
表1 车辆荷载样本特征统计Table 1 Characteristic statistics of vehicle loads sample

式中：N为应力幅值作用总次数；S为应力幅值；C为材料疲劳细节参数；m为疲劳强度曲线参数，对钢结构，一般取3.0[12]。Miner线性累积损伤理论为

式中：D为疲劳损伤度；ni为对应第 i级应力水平的应力循环数；Ni为对应第i级应力水平的疲劳寿命。由式(1)和(2)可得

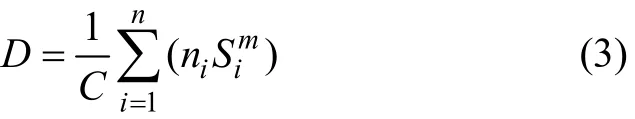
式(3)为结构疲劳损伤的计算式，其中，Si为第 i级应力幅值。若以结构的内力幅Mi作为统计参量替代Si，暂不考虑 C的影响，则可定义相对疲劳损伤 Dc描述外荷载对结构造成的损伤程度，即

式中：Dc为结构相对疲劳损伤度；Mi为第i个内力幅，对梁结构，一般为弯矩幅；Me为等效内力幅。

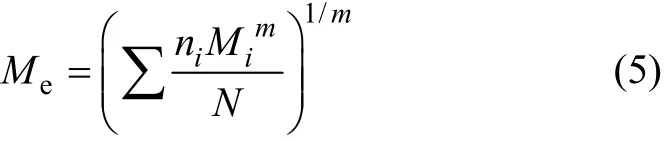
3 相对疲劳损伤度的计算

采用影响线加载及雨流法统计等传统方法对结构疲劳损伤进行精确计算不仅费时费力，而且依赖于准确的实测车辆荷载谱[13]。由于实际车辆荷载状况的复杂性和随机性，调查中很难全面、准确地统计各交通参数，且即使采用大量参数也很难准确地描述实际荷载，故很难建立荷载参数与结构疲劳损伤之间的精确关系式。但为了能简便、快捷地评估车辆荷载对结构疲劳损伤及安全可靠度的影响，采用定性分析结合数据拟合的方法，建立各主要交通车辆荷载参数与结构疲劳损伤度之间的量化估算关系式。

车辆参数对结构Dc的影响十分复杂。首先分析简支梁结构，暂不考虑多车道影响。通过对表1中采集的大量车辆 WIM 数据进行不同跨径的梁跨中截面疲劳累积损伤模拟计算，并采用雨流法计数统计其弯矩幅值和循环次数，分析不同交通参数变化下结构的相对疲劳损伤度，以获得Dc与各参量之间的关系。

3.1 桥梁跨径(影响线长度)对Dc的影响

由式(4)可知：Dc与弯矩幅Me的m次方成正比。对于简支梁结构，由结构力学，在单车轴集中荷载作用下梁跨中弯矩与跨径(影响线长度)成正比。对多轴情况，还需考虑轴距的影响。对两轴车的模拟损伤计算结果表明，Dc与桥梁跨径和平均轴距之差的m次方成正比关系。对于其他轴数车型，则可等效化为两轴车形式，即采用等效轴距的方式考虑多轴距对Dc的影响，则有 Dc∝(L -le)m。其中：L为桥梁跨径；le为等效轴距，可由各车型的最大轴距近似等效计算获得，即

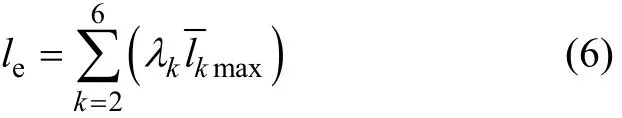
k为车型轴数，取2～6；λk为各车型数量占比；lkmax为各车型的最大轴距均值。

图1所示为雨流法计算的广东省相对疲劳损伤度与采用上述拟合公式计算的损伤度对比结果，其中m取3.0。从图1可见：采用雨流法所得结果与采用拟合公式所得结果吻合良好，也验证了Dc与 ( L - le)m成正比的关系。

图1 跨径与Dc关系曲线Fig. 1 Relationship between span and Dc

3.2 轴重力对Dc的影响

轴重力是车辆荷载最主要的参数之一。为了更有针对性，分别研究不同车型(车轴数)情况下的轴重力对结构相对疲劳损伤度的影响。首先根据各类车辆的轴重力计算获得每类车的第j轴的等效轴重力Wej[14]，即

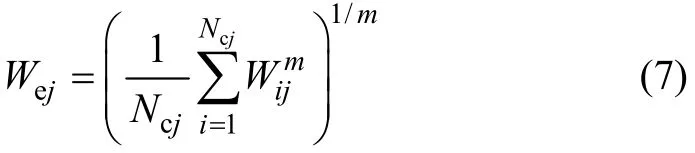
式中：Wij为各类车的第i辆车第j轴的车轴重力；Ncj为计算时间内经过桥梁的每类车的车辆数。由各轴等效轴重力求和得到每类车的等效车重力，再由下式可求得总的等效车重力We：

由结构力学可知：在结构为线弹性条件下，简支梁跨中弯矩与其上的轴重力成正比。由相对疲劳损伤度定义，Dc与轴重力的m次方成正比，考虑到轴重力与等效车重力的线性关系，则Dc也应与总等效车重力We的m次方成正比，即 D ∝Wm。

对于多车道加载情况，需要对We进行修正，可参考JTG D60—2015就多车道情况的修正系数对内力幅多车道荷载效应进行修正。

3.3 车辆数Nc对Dc的影响

由相对疲劳损伤度的定义，Dc与内力幅的总作用次数N成正比，而N取决于车辆数、轴距及车距。暂不考虑车距及轴距的影响，则内力幅作用次数N与车辆数 Nc成正比，故 Dc也与车辆数 Nc成正比，即Dc ∝Nc。

3.4 车距、轴距对Dc影响及Dc的计算式

根据上述分析，可建立单车道加载情况下简支梁跨中Dc的计算式：

式中：A为与车距、轴距及轴重力分布有关的无量纲系数，称为相对疲劳损伤系数。图2所示为不同省份车辆及不同车距作用下，采用雨流法计算获得相对疲劳损伤度后换算获得的A与桥梁跨径的关系曲线。

从图2可见： A随跨径不同分为前、后2段不同的变化趋势；车距越大，相对应的A越大，但所有曲线对应的趋势分界点基本不变。分析表明：趋势分界点L0与等效轴距有关，考虑到一般车辆轴距的范围，分界点L0偏保守，可取20 m。则根据图2可分以下2种情况进行讨论。

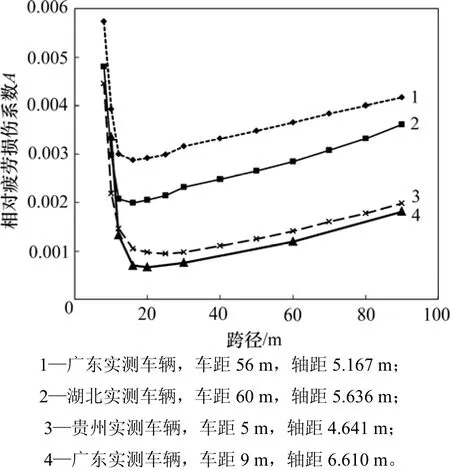
图2 A随跨径的变化曲线Fig. 2 Changing curves of A with span

1) 当L≥20 m时，A与跨径呈良好的线性关系，其变化曲线可用下面函数表示：

式中：L0=20 m；kL为拟合系数，kL=2.0×10−5；A0为跨径20 m时对应的损伤系数。计算结果如下。

① 当l/L≥1时(l为车辆平均间距)，计算表明A0取值范围为0.001～0.003，其大小与车辆轴距及轴重力分布有关，轴重力分布集中时取大值，反之取小值，故可采用等效轴距le计算确定。即当le=3.5 m时，A0取0.003，当le=7.5 m时取0.001，le在3.5～7.5之间取值时可线形内插。当无实测数据时，A0可统一取中间值0.002。

② 当l/L＜1时，A0取值需考虑车辆间距的影响。车距对Dc的影响主要体现为多车效应[14]。为了分析车距对Dc的影响，计算20 m跨径简支梁在相同车辆作用下不同车距时的梁跨中断面相对疲劳损伤度，并绘制出损伤系数A0随l/L的变化曲线，见图3。

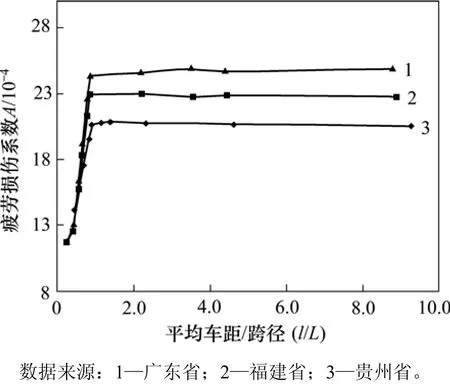
图3 20 m跨径时损伤系数A的变化曲线Fig. 3 Change curves of damage factor A for 20 m span

从图3可见：当l/L＜1时，A0与l/L呈线性变化关系，且其变化率(直线斜率)保持不变，则 A0可表达为

式中：kL0为A0对应的拟合斜率，kL0=0.002；AL0为A0对应的拟合纵截距，AL0=0.000 5。此外，当l/L≥1时，在相同车流作用下，疲劳损伤度趋于定值，即当平均车间距大于跨径时，可按单车过桥来计算结构相对疲劳损伤度，A0与车距无关。这也印证了 l/L≥1时 A0取定值的结论。

2) 当L＜20 m时，A受车辆轴距的影响较大，与跨径不再呈线性关系。

3.5 相对疲劳损伤度Dc计算式的验证

采用贵州、广东等省份采集的日交通量 WIM 数据，对跨径为20 m和40 m的简支梁，分别采用雨流统计的精确算法和式(9)对其进行疲劳损伤度计算，其中，A统一取0.002，其相对误差见表2。

从表2可见：采用式(9)计算的相对疲劳损伤值与精确损伤值较吻合，最大相对误差在10%以内。若采用实测数据特征获得的A计算，其损伤误差将更小。

表2 相对疲劳损伤度比较Table 2 Comparison of relative fatigue damage

4 车辆荷载参数与疲劳可靠度的关系

首先建立结构相对疲劳损伤度Dc与疲劳可靠度β之间的关系。根据式(3)，有

式中：Se为等效应力幅。以应力循环次数为变量，根据上式可建立结构的疲劳极限状态方程：

式中：N0为对应疲劳破坏临界状态所经历的应力幅作用总次数；D0为临界累积损伤。则桥梁某构造细节疲劳失效时的失效概率为

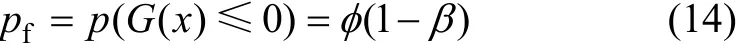
式中：β为可靠度指标；(1)φβ-为标准正态分布函数。一般地，C和 D0为随机变量且均服从对数正态分布[12−14]。根据一次二阶矩法，有

其中：0Dμ和0Dσ分别为lnC的均值和标准差；Cμ和和Cσ分别为0lnD的均值和标准差。参考美国AASHTO规范[12]，C的平均值和标准差取值见表3。

表3 AASHTO典型疲劳细节参数C取值Table 3 C values of typical fatigue detail in AASHTO MPa

NYMAN等[15−17]对大量的疲劳试验结果进行了分析，发现临界损伤D0服从对数正态分布，均值为1.0，变异系数δ为0.3。

当结构形式、尺寸和材料确定时，在疲劳荷载作用范围内，其应力幅与荷载可以假定为线性关系。对一般梁结构，荷载产生的应力幅与弯矩幅有如下关系：

式中：W为截面抵抗矩，与截面尺寸有关；Me为修正后的截面等效弯矩幅值；ks为考虑应力集中等结构尺寸效应影响的修正系数，一般可取1.0。由式(4)，(15)和(16)可得

式(17)即为结构相对损伤度Dc与疲劳可靠度β之间的关系式。将式(9)代入式(17)，化简后可得简支梁跨中截面疲劳可靠度与车辆荷载参数之间的关系式：

从式(18)可见：对特定桥梁结构，可靠度 β只与车辆数、车重力、等效轴距及车距有关。通过式(18)可分析各参数对疲劳可靠度的影响。

5 超载超限交通对疲劳可靠度的影响

5.1 荷载系数

超载超限交通对桥梁结构的损伤一直是研究者关注的重点。本文的超载超限标准是指与我国 JTG D64—2015(以下简称“规范”)中的标准疲劳荷载相比。我国规范中的疲劳验算仅考虑了交通量对疲劳强度的影响修正，本文综合考虑了车辆重力、车流交通量这2方面对疲劳损伤的影响。根据这2个参数定义荷载系数K为

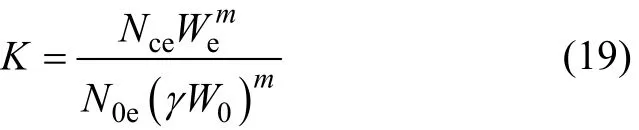
式中：Nce为实际交通流密度，可换算为日平均交通流量；We为实际车辆荷载的等效车重力；N0e为规范疲劳验算采用的标准交通流量(0.5×106)，换算到单车道日交通量为N0e=1 370 辆；W0为规范中标准疲劳车的总重，模型2取445 kN；γ为多车道效应的修正系数，可参考JTG D60—2015取值。假设评估基准期为n年，则Nc=365nNce。式(18)可化为

式(20)即为考虑了车辆超载超限时的结构疲劳可靠度计算式。

5.2 实例分析

通过 WIM 系统采集的贵州、广东等省份车辆数据，分析由这些车辆通过简支梁桥时造成的结构疲劳损伤，并计算结构的疲劳可靠度，进一步分析超载超限交通对疲劳可靠度的量化影响。

假定计算对象为设计寿命100 a的某一级公路上的1座双向4车道简支钢箱梁桥，评估基准期取设计基准期，桥梁跨径为45 m，截面抵抗矩W为0.442 m3。其箱梁截面及参数见图4。

图4 钢箱梁截面Fig. 4 Steel box girder section

对钢箱梁结构的疲劳可靠度进行评估，疲劳损伤的损伤系数A及等效轴距le由实测荷载数据确定。根据式(20)，考虑车辆超载影响，计算获得的评估基准期100 a时的该结构疲劳可靠度计算式为

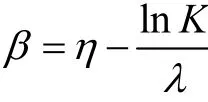
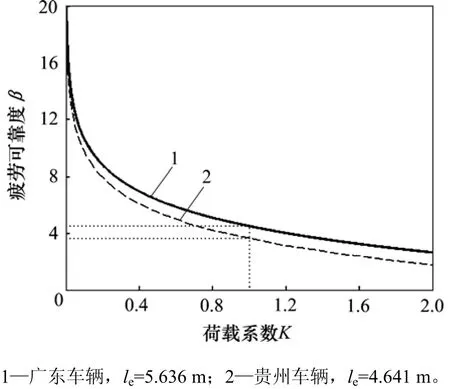
图5 荷载系数与可靠度的关系Fig. 5 Relationship between load coefficient and reliability

从图5可见：结构疲劳可靠度随着荷载系数的增加而呈对数关系降低，le越小，对应的疲劳可靠度也越小；当K=1时，对应规范标准疲劳荷载水平，其相应的结构可靠度分别为3.654和4.511。由GBT 50283—1999[18]，若考虑疲劳破坏为脆性破坏，则其目标可靠度范围为4.2～5.2，文献[5]建议桥梁疲劳目标可靠度取值为3.5，可见我国最新规范标准疲劳荷载对应的疲劳可靠度较高。随着荷载系数K增大，结构疲劳可靠度逐渐下降，当超载 10%时，对应可靠度下降到 3.5以下，当超载30%时，可靠度下降到3.0以下。

由式(20)，以 le为自变量，考虑不同超载情况计算le与疲劳可靠度之间的关系式为

式中：η′为由式(20)根据不同具体参数获得的计算值。对45 m箱梁E构造细节，根据上式绘制疲劳可靠度与等效轴距的关系如图6所示。其中K=1时的曲线对应规范标准荷载曲线，此时η′=33.30。

图6 等效轴距与可靠度的关系Fig. 6 Relationship between equivalent wheelbase and reliability

从图6可见：疲劳可靠度随等效轴距le的增大而增大，le越小，对应的疲劳可靠度越小，反之越大。由此可见：1) 较大的平均轴距对降低桥梁结构疲劳损伤有利；2) 对应常规车辆轴距(3.5～7.5 m)，其按我国规范标准疲劳荷载(K=1)计算的疲劳可靠度为3.4～4.2，进一步印证了“我国规范隐含的可靠度较高”的结论。3) 当荷载系数为1.5时，对应常规轴距的疲劳可靠度下降到 3.0以下，可见超限超载交通对疲劳可靠度的影响较大。

6 结论

1) 由实际疲劳损伤计算，采用定性分析结合数据拟合的方法，建立了车重力、车距、轴距等车辆荷载参数与结构相对疲劳损伤度之间的量化关系。

2) 基于相对疲劳损伤度与结构疲劳可靠度的关系，进一步建立了各车辆参数与疲劳可靠度之间的量化关系。根据该关系式可较简便地计算结构的疲劳可靠度，有利于快速、准确地评估桥梁结构的疲劳安全性。

3) 我国最新设计规范中疲劳标准荷载隐含的疲劳可靠度指标较高。

4) 简支梁结构的疲劳可靠度与其荷载系数的对数呈负相关关系，即随着荷载系数K增大，疲劳可靠度逐渐降低，故超限超载交通荷载将导致结构疲劳可靠度较大幅度下降。

5) 较大的车辆平均轴距对降低结构的疲劳损伤、提高结构的疲劳可靠度是有利的。

[1] 邓扬, 李爱群, 刘扬, 等. 基于监测数据的大跨度悬索桥频率与环境条件的相关性模型[J]. 中南大学学报(自然科学版),2014, 45(7): 2401−2409.DENG Yang, LI Aiqun, LIU Yang, et al. Correlation models of modal frequencies and environmental conditions for a long-span suspension bridge based on monitoring data[J]. Journal of Central South University (Science and Technology), 2014, 45(7):2401−2409.

[2] 孟阳君, 周先雁.车辆荷载作用下大跨旧桥动力可靠度研究[J].振动与冲击, 2013, 32(11): 155−156.MENG Yangjun, ZHOU Xianyan. A long-span old bridge’s dynamic reliability under vehicular load[J]. Journal of Vibration and Shock, 2013, 32(11): 155−156.

[3] JTG D64—2015, 公路钢结构桥梁设计规范[S].JTG D64—2015, Specifications for design of highway steel bridge[S].

[4] JTG D60—2015, 公路桥涵设计通用规范[S].JTG D60—2015, General code for design of highway bridges and culverts[S].

[5] 刘扬, 李胜兰, 邓杨. 超载对RC梁桥疲劳可靠性的影响分析[J]. 交通科学与工程, 2014, 30(3): 30−34.LIU Yang, LI Shenglan, DENG Yang.Influence of vehicle over load on the fatigue reliability of reinforced concrete bridge[J].Journal of Transport Science and Engineering, 2014, 30(3):30−34.

[6] 范振华, 赵亚敏. 超载运输对既有钢筋混凝土拱桥疲劳性能的影响[J]. 内蒙古公路与交通运输, 2007(4): 12−14.FAN Zhenhua, ZHAO Yamin.Influence of vehicle over load on fatigue property of reinforced concrete arch bridge[J]. Highways& Transportation in Inner Mongolia, 2007(4): 12−14.

[7] 鲁乃唯, 刘扬, 邓扬. 随机车流作用下悬索桥钢桥面板疲劳损伤与寿命评估[J]. 中南大学学报(自然科学版), 2015, 46(11):4300−4306.LU Naiwei, LIU Yang, DENG Yang. Fatigue damage and life assessment for steel decks of suspension bridge under stochastic traffic flow[J]. Journal of Central South University (Science and Technology), 2015, 46(11): 4300−4306.

[8] 王春生, 周江, 吴全友, 等. 既有混凝土桥梁疲劳寿命与使用安全评估[J]. 中国公路学报, 2012, 25(6): 101−107.WANG Chunsheng, ZHOU Jiang, WU Quanyou, et al. Fatigue life and service safety assessment for existing concrete bridges[J].China Journal of Highway and Transport, 2012, 25(6): 101−107.

[9] 李星新, 任伟新, 钟继卫. 西南山区高速公路桥梁标准疲劳车辆荷载研究[J]. 振动与冲击, 2012, 31(15): 96−100.LI Xingxin, REN Weixin, ZHONG Jiwei. Standard fatigue truck on montane speedway bridge[J]. Journal of Vibration and Shock,2012, 31(15): 96−100.

[10] HAJIALIZADEH D, OBRIEN E J, O’CONNOR A J. Virtual structural health monitoring and remaining life prediction of steel bridges[J]. Canadian Journal of Civil Engineering,2016(286): 10−14.

[11] FARRERAS-ALCOVER I, CHRYSSANTHOPOULOS M K,ANDERSEN J E. Data-based models for fatigue reliability of orthotropic steel bridge decks based on temperature, traffic and strain monitoring[J]. International Journal of Fatigue, 2017(95):104−119.

[12] AASHTO LRFD—2007, AASHTO LRFD bridge design specifications[S].

[13] 邵雨虹, 吕彭民. 九江长江大桥疲劳车辆荷载谱[J]. 长安大学学报(自然科学版), 2015, 35(5): 51−56.SHAO Yuhong, LÜ Pengmin. Fatigue load spectrum for Jiujiang Yangtzw River bridge[J]. Journal of Chang’an University(Natural Science Edition), 2015, 35(5): 51−56.

[14] 任伟平. 焊接钢桥结构细节疲劳行为分析及寿命评估[D]. 成都: 西南交通大学土木工程学院, 2009: 90−105.REN Weiping. Fatigue behaviour and fatigue life evaluation of structural details in welded steel girder bridges[D]. Chengdu:Southwest Jiaotong University. School of Civil Engineering,2009: 90−105.

[15] NYMAN W E, MOSES F. Calibration of bridge fatigue design model[J]. Journal of Structural Engineering, 1985, 111(6):1251−1266.

[16] RAJU S K, MOSES F, SCH ILLING C G. Reliability calibration of fatigue evaluation and design procedures[J]. Journal of Structural Engineering, 1990, 116(5): 1356−1369.

[17] 邓扬, 丁幼亮, 李爱群, 等. 钢箱梁桥焊接细节的疲劳断裂可靠性分析[J]. 工程力学, 2012, 29(10): 122−128.DENG Yang, DING Youliang, LI Aiqun, et al.Fracture fatigue reliability of welded details in bridge steel box girders[J].Engineering Mechanics, 2012, 29(10): 122−128.

[18] GBT 50283—1999, 公路工程结构可靠度设计统一标准.GBT 50283—1999, Unified standard for reliability design of highway engineering structures[S].

Effect of overrun and overloaded vehicles on fatigue damage and reliability of highway bridges

ZHAO Shaojie1,2,3, REN Weixin1,4

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. Communications Planning, Survey & Design Institute of Hunan Province, Changsha 410008, China;3. Hunan Provincial Key Laboratory of Highway Construction & Maintenance Technology in Southern China,Changsha 410008, China;4. School of Civil Engineering and Water Conservancy, Hefei University of Technology, Hefei 230009, China)

In order to simply and rapidly evaluate the effect of traffic load on fatigue damage of highway bridges,the relationship between vehicle load parameters and fatigue damage of structures was established by using qualitative analysis and data fitting method. Based on the limit state equation of fatigue, and considering the relationship between stress and interforce, the relationship between fatigue reliability and fatigue damage was obtained, and then the relationship between vehicle load parameters and fatigue reliability of structures was established, which provided a practical and simple method to evaluate the effect of vehicle load on fatigue damage and the reliability of structures.Based on the formula, the influence of overrun and overloaded vehicles on fatigue reliability was analyzed. The results show that the fatigue reliability of simple supported beam decreases in logarithmic form with the increase of the load coefficient K, and the larger wheel base is beneficial for decreasing fatigue damage and increasing fatigue reliability.

bridge engineering; fatigue reliability; statistical fitting; fatigue damage; overrun and overloaded vehicle

U441+.4

A

1672−7207(2017)11−3044−07

10.11817/j.issn.1672-7207.2017.11.027

2017−03−20；

2017−06−08

国家自然科学基金资助项目(51278163) (Project(51278163) supported by the National Natural Science Foundation of China)通信作者：赵少杰，博士研究生，高级工程师，从事桥梁结构安全及可靠度评估研究；E-mail: shaojiez@126.com

(编辑 陈灿华)