定常射流阵列控制地面车辆气动阻力

崔文诗，杨志刚,，王国俊

(1. 同济大学 上海地面交通风洞中心，上海，201804；2. 上海市地面交通工具空气动力与热环境模拟重点实验室，上海，201804;3. 北京民用飞机技术研究中心，北京，102211)

定常射流阵列控制地面车辆气动阻力

崔文诗1,2，杨志刚1,2,3，王国俊1,2

(1. 同济大学 上海地面交通风洞中心，上海，201804；2. 上海市地面交通工具空气动力与热环境模拟重点实验室，上海，201804;3. 北京民用飞机技术研究中心，北京，102211)

为了控制地面车辆气动阻力，通过风洞实验和大涡模拟仿真方法，研究定常射流对地面车辆流动控制的影响；研制由 17只定常射流器构成的射流阵列装置，将其安装在车辆顶部和斜背交界处，进行流动控制实验；探讨射流倾角和动量系数等射流参数对三维地面车辆的非定常流动和气动力的控制机理。研究结果表明：数值仿真方法可有效模拟气动力变化趋势。动量系数不改变气动力变化趋势，仅影响变化幅值。射流倾角决定射流出口附近的速度分布，影响气流分离，导致气动力的差异。与无控制下相比，当射流倾角为−25°～65°时，可实现减阻；而当射流倾角为80°～115°时，对应的阻力未减小。

地面车辆；定常射流；射流倾角；流动分离；气动阻力

为了控制车辆气动力，实现降低油耗和提高行驶稳定性的目的，前端扰流板、车顶涡流发生器、车底密封板、车尾隔板等被动流动控制技术已广泛应用于车辆空气动力学研发中。然而，被动流动控制技术虽具有可靠性，但控制效率低，且需安装气动附件，影响整车造型[1−2]。主动流动控制技术可以克服以上缺点，BRUNEAU 等[3−6]分别利用直接数值模拟(DNS)、雷诺平均法(RANS)、大涡模拟(LES)等数值仿真方法，基于定常射流技术对车辆开展气动阻力控制研究。2011年以来，随着实验技术的发展，MCNALLY 等[7−11]应用微型喷头对不同车辆简化模型的流动进行实验控制研究。以上研究都是基于射流方向与斜背垂直的单一工况展开分析的。针对以往研究未给出射流倾角变化导致的气动力和流场差异及其内在作用机理的问题，本文作者通过数值仿真和风洞实验，分析射流参数对车辆气动阻力控制的影响，首先给出射流倾角和动量系数等参数对气动力和流场的控制结果和变化规律，然后分析射流参数变化导致气动力存在差异的原因。

1 模型和风洞实验

1.1 车辆模型

车辆外流是包含地面效应、三维、非定常、气流分离等现象的复杂流动[11]。Ahmed body模型[12]可有效模拟不同车辆尾部倾角下的气动力性能和复杂流场。采用1/3缩比的Ahmed body模型作为研究对象，风洞实验模型如图1(a)所示。模型尾部倾角为25°，尺寸如图1(b)所示，长L=0.348 m， 宽W=0.130 m，高H=0.096 m，将轮胎简化为圆柱杆，其直径为0.01 m，离地间隙为0.017 m。

图1 车辆简化模型和尺寸Fig. 1 Simplified vehicle model and dimensions

1.2 定常射流阵列

对车辆的流动控制通过定常射流阵列系统实现，如图2所示，该系统包括空压机及压力表、调压阀、减压器及压力表、扩张阀、射流管道(内钢管、软管和外钢管)和带射流孔的固定支架构成。通过减压器调节系统到标定压力，在射流孔下游2 mm处利用热线风速仪测试射流出口速度，实验中标定的射流速度v分别为3 m/s和6 m/s。

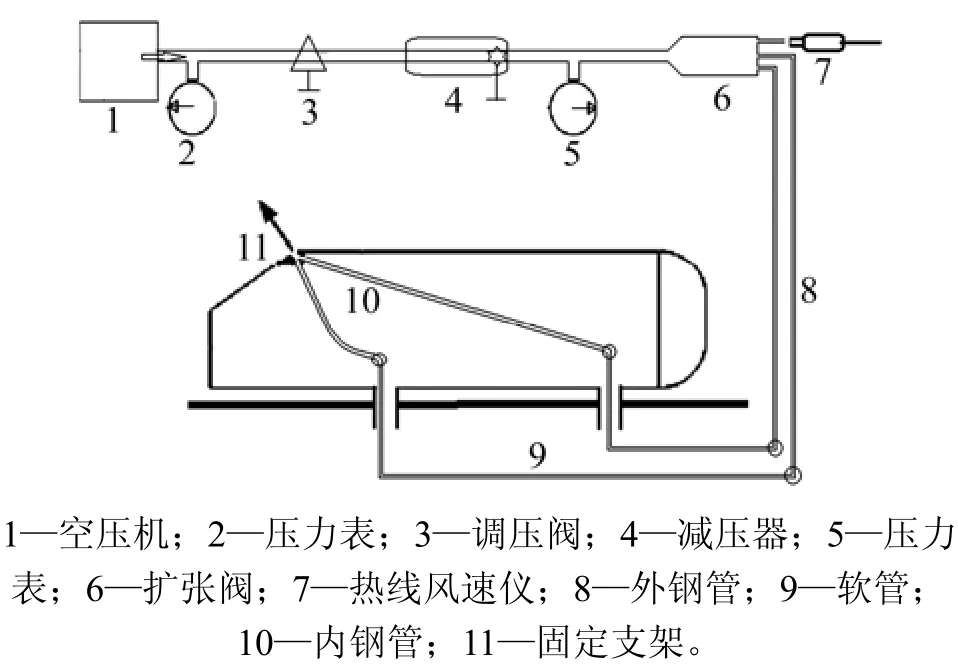
图2 定常射流阵列系统Fig. 2 Steady blowing array system

图 3(a)所示为射流阵列在车辆上的布置方案。其在车辆斜背和顶盖交界处开槽，将射流器系统安装在车辆模型内。GODARD等[13]认为分离控制最优结果对应的圆孔直径与间距比应为0.2。

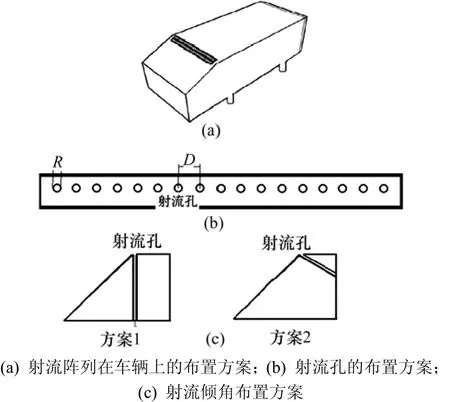
图3 定常射流阵列的布置方案Fig. 3 Arrangement of steady blowing array system

本文射流出口的圆孔直径R设计为1.2 mm，相邻圆孔中心点距离D为6 mm。图3(b)所示为在射流器固定支架上开17只等直径的射流孔的布置方案。将钢管安装于固定支架的射流孔内，形成完整的射流器系统。制作了 2套固定支架方案(方案 1和方案 2)这 2套方案的设计可保证射流方向仅在xOz面内，定义射流方向与x正向的夹角为射流倾角β，如图3(c)所示，方案1和方案2对应的射流倾角分别为90°和25°。

1.3 风洞实验

实验在上海地面交通工具风洞中心整车的1/15缩比模型风洞完成。模型风洞最大风速为48 m/s，喷口面积为0.123 m2，目前试验段的湍流强度为0.38%[14]。支撑杆内部为中空结构，内、外径分别为 5 mm和10 mm，测压钢管或射流管道可穿过支撑杆与车辆连接，不干扰车辆外部流场。如图 1(a)所示，车辆模型通过支撑杆固定在槽钢上，槽钢和盒式应变天平通过螺栓连接，一起固定于支架上。通过以上机构，天平可测量车辆模型的阻力。在车身表面布置了30个测压孔，位置如图1(b)所示。将测压钢管的一端固定于测压孔，另一端与软管相连，接在多通道的压力采集系统上，测量表面静压，采样时间为40 s。

首先，进行车辆在无控制下的风洞实验，测试阻力和表面压力。然后，进行有射流控制下的阻力实验，由于方案1和方案2都需将射流管道经过支撑杆安装在车表面，但支撑杆内径无法满足测压钢管和射流管道同时插入的条件，故射流控制实验中仅测试了阻力。保证在有无流动控制下的风洞实验来流风速 U=20 m/s，基于模型车长的实验雷诺数 ReL=4.7×105，定义射流动量系数Cμ[5−6]为

式中：W和H分别为车辆模型的宽和高；v为射流出口速度。因此，v为3 m/s和6 m/s时，动量系数Cμ1和 Cμ2分别为 2.35×10−3和 4.7×10−3。

2 数值仿真与结果验证

2.1 数值仿真方法

数值仿真的雷诺数与实验所得一致。依据车体尺寸，确定计算域长、宽和高分别为8L，7W和5H。由于六面体网格收敛性好，故流场空间采用六面体非结构化网格划分。按照大涡模拟对网格的要求，保证第一层网格尺寸y+小于1，如图4所示。对车体近壁面、射流孔附近的剪切层、斜背和近尾迹区进行加密，以便能够捕捉更多流动结构。表面网格尺寸为 0.1～1.5 mm，有无控制下网格总数保持一致，体网格总数为2 100万个，继续增加网格数对计算结果影响很小。

图4 加密体网格Fig. 4 Refined volume mesh

MINGUEZ等[15−16]指出RANS无法有效模拟大分离流动结构，但大涡模拟可以较好地模拟斜背大分离及其附着流动，因此，本文作者使用商业软件 Fluent 12.1进行大涡模拟的并行计算。采用WALE亚格子模型，迭代方法为 SIMPLEC算法，计算时间步长为0.1 ms。地面和车身采用无滑移边界条件，根据实验测得的射流器出口速度剖面，加载到壁面指定网格，形成射流入口条件。为保证数值求解精度，所有监测的流场参数满足相应的收敛条件。

2.2 仿真结果验证

在无控制的条件下，实验测得阻力系数为0.365，仿真计算值为0.372。对车身不同位置的测压点进行比较，如图5所示，仿真得到的压力系数与实验结果较吻合。在有控制的实验中，当施加动量系数为 Cμ1，β=90°时，阻力增大，而当β=25°时阻力减小。当增大动量系数到 Cμ2，β=90°时，阻力进一步增大，而当β=25°时，阻力减小得更多。数值仿真模拟了不同射流倾角下阻力的变化趋势，可有效预测射流对车辆的流动控制作用。因此，以下讨论皆使用此仿真方法进行计算。

3 仿真结果分析

3.1 阻力系数比较

图6所示为不同射流倾角和动量系数下的阻力系数。由图6可知：−25°≤β≤65°为减阻区，在各射流倾角(−25°, 0°, 25°, 45°, 65°)下阻力均减小，当 β=0°时，减阻幅度达到最大。当0°≤β≤65°时，随着β增大，阻力增大。减小动量系数使减阻幅度降低，而当β=80°时，阻力与无控制下阻力近似。90°≤β≤115°为增阻区，各射流倾角(90°, 100°, 115°)作用下的阻力皆高于无控制下的阻力，随着β增大，阻力减小。

图5 表面压力系数对比Fig. 5 Comparison of surface pressure coefficient

3.2 不同射流倾角比较

以下将有无控制下的流场进行比较，分析同一动量系数Cμ2下，不同射流倾角β导致车辆的气动阻力行为存在差异的原因。

图7所示为面y=0 m上的射流出口附近的速度与流线。由图7可知：当β=65°时，与无控制下的流场相比，射流入口附近的流向速度增大，速度梯度曲线饱满，边界层内动量增加，抵抗逆压梯度的能力增强。同时，在射流作用下，分离点后移至斜背上，流动分离减弱。图8所示为斜背y=0 m上的回流区。由图8可知：附着位置从无控制下对应点(x=0.828 5 m，z=0.090 5 m)上移至点(x=0.827 2 m，z=0.091 1 m)，回流区减小；图9和图10所示分别为涡量分布及表面平均压力分布。由图9可知：涡量(涡量Q准则[16])减小，斜背压力升高。在回流区外，附着流的速度增大导致后垂直背上端的气流速度随之增大，上端气流分离作用减弱，后垂直背压力升高，实现减阻。

图6 不同射流倾角和动量系数下的阻力系数Fig. 6 Drag coefficient in different jet directions and momentum coefficients

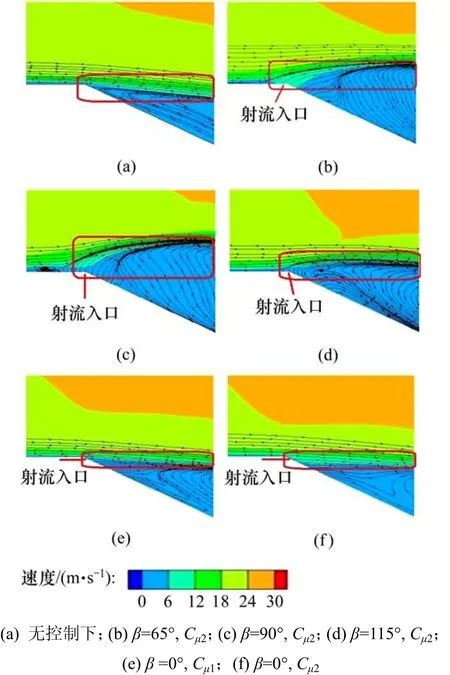
图7 面y=0 m上的射流出口附近的速度与流线Fig. 7 Mean velocity distribution and streamlines near jet exit on plane y=0 m

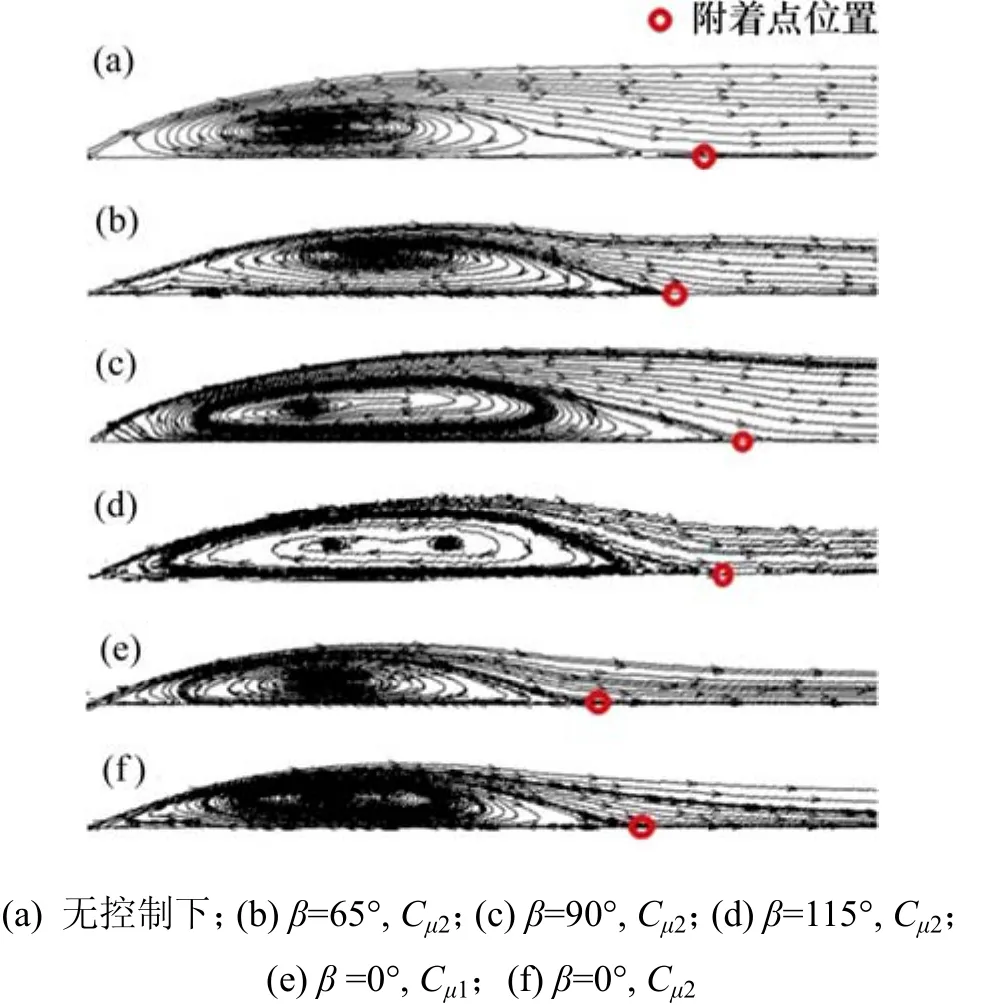
图8 斜背y=0 m上的回流区Fig. 8 Recirculation zone on plane y=0 m of rear slant

图 9 涡量分布(Q=4.7×105 s−1)Fig. 9 Vortices distribution (Q=4.7×105 s−1)

由图7～9可知：与无控制下的流场相比，当β=90°时，射流入口附近的外流急剧上扬，导致流向速度减小，边界层内动量减小，抵抗逆压梯度的能力减弱。同时，射流入口处的速度梯度为 0，分离点前移至车顶，加剧了流动分离，气流附着位置下移至点(x=0.833 7 m，z=0.087 9 m)，回流区扩大，涡量增大，斜背负压区扩大。回流区的扩大导致回流区外附着流的速度降低，后垂直背上端的气流分离加剧，涡量增大，压力减小，阻力增大。

图10 表面平均压力分布Fig. 10 Mean surface pressure distribution

当β=115°时，如图7所示，由于射流倾角的差异，导致射流入口附近的流向速度低于无控制工况的速度，高于β=90°工况的速度。因此，如图8～10所示，β=115°工况的回流区范围、涡量，斜背和后垂直背上的压力介于无控制和 β=90°工况对应值之间，导致了β=115°工况的阻力也处于2工况之间。

3.3 不同动量系数比较

以切向吹气(β=0°)为例，分析不同动量系数对阻力的影响。当动量系数从Cμ1增大到Cμ2时，射流入口附近的流向速度增大，边界层动量增加，抵抗逆压梯度的能力增强，附着位置从点(x=0.824 2 m, z=0.092 5 m)上移至点(x=0.820 9 m, z=0.094 1 m)，回流区减小, 涡量减小, 斜背压力升高，阻力进一步减小。

4 结论

1) 在车辆的斜背与顶盖交界处，安装定常射流阵列，射流倾角决定了气动力行为(增阻或减阻)。其中，−25°≤β≤65°为减阻区，当 β=0°时，阻力达最小，当β=80°时，阻力与无控制下的阻力相当；而 90°≤β≤115°为增阻区，皆高于无控制下的阻力，随着β增大，阻力减小。

2) 在同一动量系数下，射流倾角造成车辆气动力存在差异的原因是：射流入口附近流向速度的差异，导致边界层抵抗逆压梯度的能力不同，进而使流动分离所致的斜背回流区存在差异。

3) 改变动量系数主要影响气动力变化量，在减阻区，增大动量系数可获得更高幅度的减阻。

[1] 杨易, 徐永康, 沈夏威, 等. 基于气动升力的汽车底部流场改进[J]. 中南大学学报(自然科学版), 2013, 44(10): 4063−4068.YANG Yi, XU Yongkang, SHEN Xiawei, et al. Improved research of automobile underbody flow filed based on aerodynamic lift improved research of automobile underbody flow filed based on aerodynamic lift[J]. Journal of Central South University (Science and Technology), 2013, 44(10): 4063−4068.

[2] CHOI H, LEE J, PARK H. Aerodynamics of heavy vehicles[J].Annual Review of Fluid Mechanics, 2014, 46(1): 441−468.

[3] BRUNEAU C H, CREUSE E, DEPEYRAS D, et al. Coupling active and passive techniques to control the flow past the square back Ahmed body[J]. Computers & Fluids, 2010, 39(10):1875−1892.

[4] ROUMEAS M, GILLIERON P, KOURTA A. Analysis and control of the near-wake flow over a square-back geometry[J].Computers & Fluids, 2009, 38(1): 60−70.

[5] WASSEN E, THIELE F. Drag reduction for a generic car model using steady blowing[C]//4th Flow Control Conference. Seattle,Washington: AIAA, 2008: 1−12.

[6] WASSEN E, THIELE F. Road vehicle drag reduction by combined steady blowing and suction[C]//39th AIAA Fluid Dynamics Conference. San Antonio, Texas: AIAA , 2009: 1−9.

[7] MCNALLY J, FERNANDEZ E, KUMAR R, et al. Near wake dynamics for an Ahmed body with active flow control[C]// 6th AIAA Flow Control Conference. New Orleans, Louislana: AIAA,2012: 1−11.

[8] AUBRUN S, MCNALLY J, ALVI F, et al. Separation flow control on a generic ground vehicle using steady microjet arrays[J]. Experiments in Fluids, 2011, 51(5): 1177−1187.

[9] MCNALLY J, FERNANDEZ E, ROBERTSON G. Drag reduction on a flat-back ground vehicle with active flow control[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 145: 292−303.

[10] LITTLEWOOD R P, PASSMORE M A. Aerodynamic drag reduction of a simplified squareback vehicle using steady blowing[J]. Experiments in Fluids, 2012, 53(2): 519−529.

[11] ZHANG B F, ZHOU Y, TO S. Unsteady flow structures around a high-drag Ahmed body[J]. Journal of Fluid Mechanics, 2015,777: 291−326.

[12] AHMED S R, RAMM R, FALTIN G. Some salient features of the time-averaged ground vehicle wake[C]//International Congress&Exposotion. Detroit, Michigan: AIAA, 1984: 1−34.

[13] GODARD G, STANISLAS M. Control of a decelerating boundary layer. Part 3: optimization of round jets vortex generators[J]. Aerospace Science and Technology, 2006, 10(6):455−464.

[14] 崔文诗, 杨志刚, 朱晖. 合成射流对类车体流动控制的影响[J]. 同济大学学报(自然科学版), 2016, 44(6): 937−943.CUI Wenshi, YANG Zhigang, ZHU Hui. Influences of a synthetic jet actuator on the flow around Ahmed body[J]. Journal of Tongji University (Natural Science), 2016, 44(6): 937−943.

[15] MINGUEZ M, PASQUETTI R, SERRE E. High-order large-eddy simulation of flow over the “Ahmed body” car model[J]. Physics of Fluids, 2008, 20(9): 095101.

[16] KRAJNOVIC S, DAVIDSON L. Flow around a simplified car.Part 2: understanding the flow[J]. Journal of Fluids Engineering Transactions of the Asme, 2005, 127(5): 919−928.

Aerodynamic drag control of a ground vehicle using steady blowing array

CUI Wenshi1,2, YANG Zhigang1,2,3, WANG Guojun1,2

(1. Shanghai Automotive Wind Tunnel Center, Tongji University, Shanghai 201804, China;2. Shanghai Key Lab of Vehicle Aerodynamics and Vehicle Thermal Management Systems，Shanghai 201804, China;3. Beijing Aeronautical Science & Technology Research Institute, Beijing 102211, China)

In order to control the aerodynamic drag of a ground vehicle, the effect of steady blowing array on the flow over a ground vehicle was investigated through the wind tunnel experiments and large eddy simulations. The array device composed of 17 steady blowing jets was developed, which was set on the junction between the slant and the roof of a ground vehicle, and the flow control experiments were carried out. The control mechanism of the excitation parameters,such as the jet direction angle and momentum coefficient, on the unsteady flow and aerodynamics forces of a three dimensional ground vehicle were discussed. The results show that the numerical simulation can effectively simulate the trend of the aerodynamic force. The momentum coefficient can only affect the amplitude of variation in aerodynamic drag, not the tendency of drag variation. The jet obliquity dominates the velocity distribution near the jet exit, which has an influence on the flow separation and leads to the variation of aerodynamic drag. Compared with natural flow, the jet obliquities from −25° to 65° help drag reduction, while the jet obliquities from 80° to 115° make no difference to relevant drag.

ground vehicle; steady blowing; jet direction; flow separation; aerodynamic drag

U270.1；O357.5+2

A

1672−7207(2017)11−2912−06

10.11817/j.issn.1672-7207.2017.11.010

2016−11−29；

2017−01−10

上海市地面交通工具风洞中心专业技术服务平台资助项目(14DZ229140) (Project(14DZ229140)supported by the Professional Technical Service Platform of Shanghai Automotive Wind Tunnel Center)

杨志刚，博士，教授，从事汽车空气动力学研究；E-mail: zhigang.yang@sawtc.com

(编辑 刘锦伟)