自锚式悬索桥吊杆张拉过程结构响应规律

黄少华，魏家乐

(1.中交隧道局第二工程有限公司，陕西 西安 710100； 2.陕西通宇公路研究所有限公司，陕西 西安 710100)

自锚式悬索桥吊杆张拉过程结构响应规律

黄少华1，魏家乐2

(1.中交隧道局第二工程有限公司，陕西 西安 710100； 2.陕西通宇公路研究所有限公司，陕西 西安 710100)

针对自锚式悬索桥施工控制过程中吊杆张拉繁琐、控制难度较高、结构响应规律复杂等问题，对依托工程空间索面自锚式悬索桥建立有限元模型，并提出合理的张拉控制方案。结果表明：吊杆张拉过程中，主缆呈现出明显的大位移非线性特点，吊杆之间相干性显著、复杂，索塔的受力安全需要合理的索鞍顶推才能保证，加劲梁逐渐脱离支架实现体系转换，临时和永久支座反力变化明显。

自锚式悬索桥；结构响应；有限元分析；吊杆张拉

0 引 言

自锚式悬索桥主缆直接锚固在主梁上，主缆的水平分力由主梁直接承受，因此主梁必须先于主缆施工。主梁的施工方法一般有支架架设法、节段吊装法、顶推架设法和斜拉扣挂法等。在梁、缆都施工完成后再进行吊杆张拉，这是自锚式悬索桥最关键的步骤，从而完成体系转换。文献[1]～[5]给出了主梁脱架状态的确定方法，研究在约束条件限值下，吊杆张拉次数和接长杆数量比选的基本原则与方法。文献[6]以江东大桥为依托，研究吊杆张拉过程中缆索系统的受力特性，发现在吊杆张拉过程中，主缆的线形，内力、吊杆力、加劲梁的线形和内力，以及索鞍和索塔的位置等多参数耦合的影响下，结构受力复杂。文献[7]介绍一种降温法模拟调整吊杆无应力长度的方法，实现吊杆张拉过程体系转换，并对结构受力特点进行了分析。文献[8]～[11]依据桥梁缩尺模型试验测试了体系转换过程中吊杆索力、主缆线形、索塔及加劲梁的响应规律。

综上所述，自锚式悬索桥吊杆张拉体系转换过程中，各种非线性问题突出[12-13]，在一定张拉设备下如何用尽量少的吊杆张拉次数使最终索力达到设计值是一道难题；且对于空间索面自锚式悬索桥，由于主缆、吊杆、加劲梁及索塔等多参数高度耦合，体系转换过程中结构响应更为复杂，故目前研究较少涉及。本文通过有限元手段对吊杆张拉过程中主缆的大位移非线性、吊杆索力的相干性、索塔的变位和受力、加劲梁的变形和受力、永久和临时支点的反力变化等结构响应规律进行研究，最终使受力及线形满足施工及成桥状态要求。

1 工程背景及有限元模型的建立

青岛海湾大桥大沽河航道桥为独塔自锚式悬索桥，跨径布置为80 m+190 m+260 m+80 m。该桥采用四跨连续半漂浮体系，主跨及边跨均为悬吊结构，桥型布置如图1所示。主缆边跨矢跨比为1/18.04，主跨矢跨比为1/12.53。主缆为2根空间缆，横桥向间距在塔顶处为2.5 m，在边跨侧后锚面为7.8 m，在主跨侧后锚面为6.5 m。边跨及主跨均设置吊杆，名义水平间距为12 m。边跨有12对吊杆，主跨有17对吊杆，从青岛侧向黄岛侧编号依次为B1～B12、Z1～Z17。

采用空间有限元程序MIDAS/Civil建立模型进行结构分析，模型共有单元540个，节点602个，结构离散图如图2所示，模型包含索塔、加劲梁、主缆和吊杆等。在模型中，索塔和加劲梁采用梁单元模拟，主缆和吊杆采用只受拉索单元模拟，支架采用弹簧单元模拟，压重采用集中荷载进行模拟。

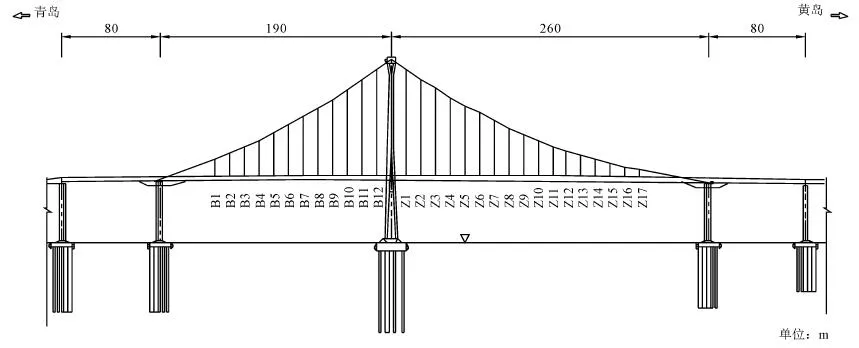
图1 大沽河航道桥桥型布置(立面)

图2 结构离散图

2 吊杆张拉特点

自锚式悬索桥空缆状态与成桥状态主缆线形相差巨大，大沽河航道桥的竖向变形达到近4 m，因此在吊杆张拉过程中需要接长。由于张拉设备的数量和能力、吊杆承载力、主塔和加劲梁的承载力等各种因素的限制，全桥的吊杆需要多次分级张拉才能达到设计值。理想的方法是将吊杆无限次均匀张拉至设计值，但实际施工中将全桥吊杆张拉1遍需要花费漫长时间，这一过程包括千斤顶的安装与挪动和接长杆的安装与拆卸等，占用大量的人力、物力，工期和造价方面都无法接受。因此，如何用尽量少的吊杆张拉次数使最终索力达到设计值是吊杆张拉过程中的重要问题。

另外，吊杆张拉过程中各种非线性问题突出，如主缆大位移非线性、吊杆的参与和退出工作、吊杆间力的强相干性、主缆与鞍座接触非线性、索鞍的顶推非线性，加劲梁与支架的接触非线性、主塔和加劲梁的梁柱P-Δ效应非线性和混凝土材料的收缩徐变非线性等。所有这些非线性相互耦合作用使得吊杆张拉过程的计算极其复杂，在分析方法上与地锚式悬索桥差异巨大。

3 吊杆张拉方案

对于自锚式悬索桥，将吊杆一次均匀张拉至设计值是最理想的方法，但造价较高；多次分级张拉势必会降低张拉效率。因此，制定一套好的吊杆张拉方案非常重要[14-16]。

本文对于大沽河航道桥，采用12台千斤顶对3种不同编号的吊杆同时张拉，提出一套安全可行的吊杆张拉方案，张拉步骤见表1。

大沽河航道桥吊杆张拉过程主要控制因素为，吊杆张拉次数及最大张拉力、接长杆数量、索鞍顶推次数、索塔塔顶最大位移、索塔根部应力、加劲梁应力、支点反力、配重时机。通过对上述张拉方案进行详细的计算与分析，各控制因素控制效果较好：吊杆通过15次张拉全部到位，索鞍通过2次顶推复位，临时支架(支撑)通过5次全部拆除，压重通过20次全部施加；吊杆的最大张拉力为3 068 kN，最大应力为646.0 MPa，安全系数大于2.59；索塔的纵桥向最大位移为21.9 cm，最大压应力为13.0 MPa，最小压应力为0.4 MPa，未出现拉应力；加劲梁最大压应力为100.1 MPa，最大拉应力为89.7 MPa，满足规范要求；临时支点反力均不超过其加强构造承载力；永久支座反力均不超过其容许承载力，且有一定安全储备，其中索塔三角撑永久支座上的最小储备为427 t；索鞍2次顶推复位，最后一次顶推在第7次吊杆张拉之后；考虑到压重需人工施加，速度较慢，结合吊杆张拉方案，将青岛侧锚固区压重1 541 t分15次施加，每次102.7 t，索塔塔区压重544 t分5次施加，每次108.8 t，这样施工单位有充分的时间施加压重；吊杆倾斜角度在吊杆锚固钢导管允许的转角范围内，且有较大富余，最小富余量为3.2 cm；吊杆长度不够时通过接长杆方式接长，接长杆采用分段制造，每段长1 m，最多使用44根接长杆。

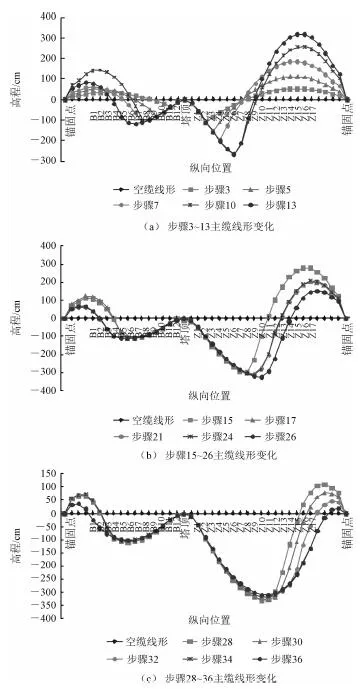
图3 主缆在各吊杆张拉步骤的线形变化

4 主缆大位移非线性响应

主缆作为悬索桥的主要承重构件，具有柔性几何可变性，其自身的弹性变形和几何形状的改变都可影响结构体系的平衡，表现出的大位移非线性力学响应是自锚式悬索桥最主要的非线性影响因素之一[17]。在施工过程中，通过对全桥若干吊杆的逐渐张拉，主缆的线形由空缆状态逐渐逼近成桥状态，最终实现体系转换。

按上述方案对吊杆张拉过程中的主缆变形进行分析计算，主要张拉阶段主缆高程变化如图3所示。

表1吊杆张拉步骤

施工阶段施工步骤施工内容备注吊杆张拉前0索塔施工完毕,加劲梁安装完毕,索塔鞍座安装并设置预偏,主缆架设完毕,索夹、吊杆安装完毕吊杆张拉过程1拆除2个过渡墩上的临时支撑第1次拆除支架(支撑)2青岛侧锚固区压重102.7t第1次施加锚固区压重3将吊杆B12、Z1、Z2张拉到位第1次张拉吊杆4青岛侧锚固区压重102.7t第2次施加锚固区压重5将吊杆B11、B10、Z3张拉到位第2次张拉吊杆6青岛侧锚固区压重102.7t第3次施加锚固区压重7将吊杆B8、B9、Z4张拉到位第3次张拉吊杆8青岛侧锚固区压重102.7t第4次施加锚固区压重9拆除塔区(302#)支架第2次拆除支架10将吊杆Z5、Z6张拉到位,Z7张拉到1000kN第4次张拉吊杆11青岛侧锚固区压重102.7t第5次施加锚固区压重12索鞍顶推14.2cm第1次顶推索鞍13将吊杆B6、B7张拉到位,B5张拉到1000kN第5次张拉吊杆14主塔塔区压重108.8t第1次施加塔区压重15将吊杆Z7张拉到位,Z8张拉到3000kN,Z9张拉到2500kN第6次张拉吊杆16主塔塔区压重108.8t第2次施加塔区压重17将吊杆Z9张拉到2500kN,Z10张拉到2500kN,Z11张拉到2500kN第7次张拉吊杆18主塔塔区压重108.8t第3次施加塔区压重19索鞍顶推24cm,索鞍复位第2次顶推索鞍20拆除临时墩一、边跨锚固段(301#)支架和临时墩二第3次拆除支架21将吊杆B5、B4张拉到位、B3张拉到2000kN第8次张拉吊杆22主塔塔区压重108.8t第4次施加塔区压重23拆除临时墩六、边跨锚固段(303#)支架和临时墩七第4次拆除支架24将吊杆Z8、Z9张拉到位,Z10张拉到3000kN第9次张拉吊杆25主塔塔区压重108.8t第5次施加塔区压重26将吊杆Z10张拉到位,Z11张拉到3000kN,Z12张拉到3000kN第10次张拉吊杆27青岛侧锚固区压重102.7t第6次施加锚固区压重28将吊杆Z11张拉到位,Z12张拉到3000kN,Z13张拉到3000kN第10次张拉吊杆29青岛侧锚固区压重102.7t第7次施加锚固区压重30将吊杆Z12张拉到位,Z13张拉到3000kN,Z14张拉到2500kN第12次张拉吊杆31青岛侧锚固区压重102.7t第8次施加锚固区压重32将吊杆Z13、Z14张拉到位,Z15张拉到3000kN第13次张拉吊杆33青岛侧锚固区压重102.7t第9次施加锚固区压重34将吊杆Z15、Z16、Z17张拉到位第14次张拉吊杆35青岛侧锚固区压重102.7t第10次施加锚固区压重36将吊杆B3、B2、B1张拉到位第15次张拉吊杆37青岛侧锚固区压重513.7t第11～15次施加锚固区压重38拆除临时墩三、四、五,吊杆张拉结束第5次拆除支架吊杆张拉后39施工桥面系等附属工程40吊杆微调

通过计算分析可知，吊杆张拉过程中主缆位移变化的主要规律如下：主缆在吊杆张拉过程中的位移变化巨大，呈现出显著的大位移非线性特点，在本方案中主缆累计位移变化达到3.3 m；主缆在开始张拉时索力和刚度较小，每步变形较大；在逐渐张拉过程中索力和刚度也逐渐增大，每步变形逐渐变小；主缆在每步张拉中，张拉点位移变化较大，主缆单次位移变化最大超过2 m，附近点位移逐渐减小；同跨远离张拉点的部分点出现明显的反向位移(最大达到-3.2 m)，后逐渐恢复正向位移；在后续吊杆张拉过程中，由于吊杆的限制，张拉过的节点位移基本不再发生较大变化；在开始张拉过程中，主缆张拉点可能出现位移拐点，应注意观察以防止鼓丝情况出现；吊杆张拉过程中，由于主缆为空间缆，除了出现竖向位移，还将出现较大的纵横向位移(本桥纵向位移最大超过1.5 m)，因此需注意吊杆倾斜角度在吊杆锚固钢导管允许的转角范围内。

5 吊杆索力相干性响应

对于自锚式悬索桥，吊杆张拉实现了体系转换，是桥梁施工的关键工序，由于索力间的相互影响，吊杆张拉也是全桥的控制难点。由于主缆是柔性结构，吊杆张拉过程中主缆变形较大，后张拉的吊杆会对之前张拉的吊杆产生较大影响，其相干性非常明显。

按上述方案对吊杆张拉过程中的吊杆索力进行分析计算，主要张拉阶段吊杆索力变化如图4、5所示。

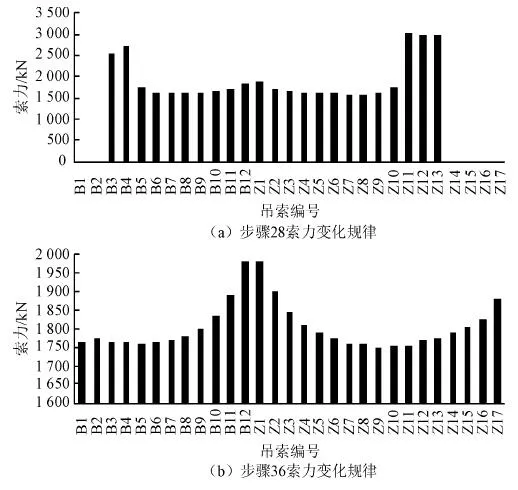
图4 张拉步骤28、36的吊杆索力

图5 吊杆在不同阶段的索力变化

通过计算分析可知，自锚式悬索桥在吊杆张拉过程中，吊杆索力变化的主要规律如下：吊杆索力在张拉过程中变化较大，无论张拉方式如何，最大出现索力(而非最大张拉索力)均需满足一定安全系数；主缆在开始张拉时刚度较小，吊杆可以一步张拉到位，但在逐渐张拉过程中主缆刚度逐渐增大，为保证吊杆索力在安全范围，部分中部区域吊杆需多次张拉才能张拉到位；张拉吊杆对附近已张拉点索力影响巨大，往往出现急剧减小现象(即卸载现象，这对无法一次张拉到位的吊杆提供了解决办法)，而远离张拉点索力却出现逐渐增大现象，中间点索力逐渐过渡变化；吊杆张拉会引起索塔偏向张拉跨，这将导致邻跨主缆垂度减小和吊杆索力的增大，因此相邻跨吊杆需交替张拉以保证已张拉的吊杆索力不会超限；由于吊杆索力的相干性，张拉阶段往往容易忽视部分吊杆可能出现的索力过小情况，应保证最小索力在一定安全范围，防止吊杆过小导致锚头偏移或倾斜；由于主缆大变位影响，张拉前主缆上的吊点到加劲梁锚固点的距离大于吊杆长度，必须设置接长杆将吊杆锚头张拉至锚点。为了方便使用及节省材料，接长杆可采用分段设计，在使用时按需接长。

6 索塔变位响应

在自锚式悬索桥吊杆张拉过程中，索塔两侧主缆的水平分力发生不对等的增长，空缆状态预偏索鞍时索塔的平衡状态逐渐被打破，索塔发生偏位，塔身出现不对称的受力，需要及时对索鞍进行顶推以保证索塔得到新的平衡状态。

按上述方案对吊杆张拉过程中的索塔进行分析计算，主要张拉阶段索塔塔顶变位及应力极值如图6、7所示。

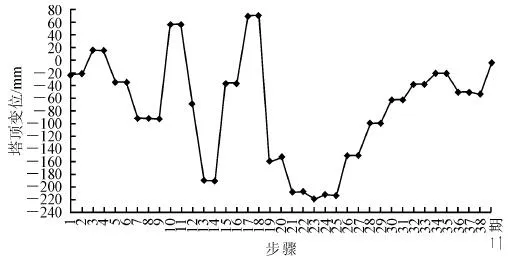
图6 索塔塔顶纵桥向变位规律

图7 索塔塔身应力极值

索塔变位和受力主要规律如下：索塔在吊杆张拉前的空缆状态时，塔顶索鞍进行预偏，保证主缆在索塔两侧水平分力平衡，索塔不受水平不平衡力影响，结构受力安全。但需注意，索塔此时为偏心受压状态，因此空缆状态索塔塔顶仍有近2 cm位移；吊杆张拉应保持相邻跨交替进行，以保证索塔不会出现较大的不平衡力。由于主边跨跨径不等，在吊杆张拉过程中主缆水平分力平衡状态被打破，索塔在塔顶的竖向和水平分力均逐渐增大，到一定程度时需进行索鞍顶推以释放新的不平衡水平力，保证索塔受力安全；索鞍顶推会造成索塔应力的急剧变化，因此需保证索塔有足够的应力储备，以防止混凝土索塔开裂。为提高张拉效率，索鞍顶推次数越少越好，且应保证索鞍尽早顶推到位，防止塔顶主缆竖向分力过大导致索鞍难以顶推在吊杆张拉完毕的成桥状态，索鞍处于索塔中心，索塔平衡受力，塔顶位移为0 cm，塔身应力对称。

7 加劲梁的变形响应

吊杆张拉的过程也是加劲梁自重由支架向主缆转换的过程，这一过程的初期由于被张拉吊杆的拉力往往较小，所以吊杆的张拉不会对加劲梁的受力产生明显的影响，而随着吊杆的不断张拉，加劲梁的自重由单纯支架支承变为支架与主缆共同支承，进而最后变为加劲梁完全脱离支架，由主缆完全承受，从而实现体系转换，这期间加劲梁的受力状态会发生较大变化。

按上述方案对吊杆张拉过程中的加劲梁进行分析计算，主要张拉阶段加劲梁高程变化及应力极值如图8、9所示。

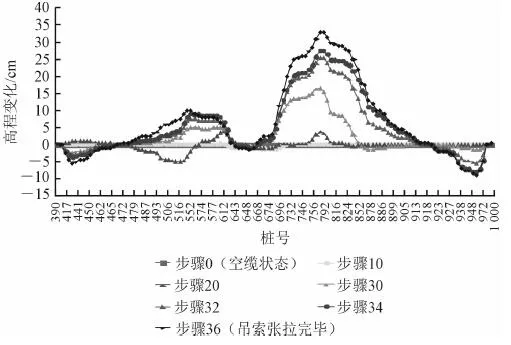
图8 加劲梁在各吊杆张拉步骤的高程变化

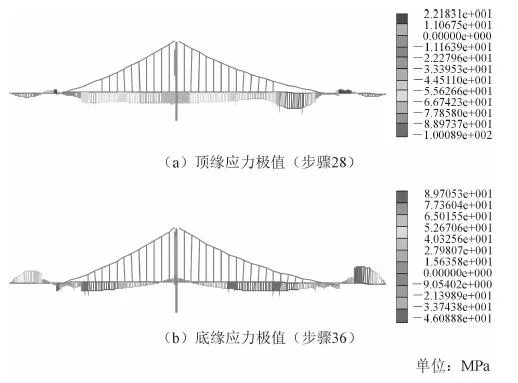
图9 加劲梁在吊索张拉过程的应力极值

通过计算分析可知，在吊杆张拉过程中，自锚式悬索桥加劲梁变形和受力的主要变化规律如下：由于吊杆力需要克服加劲梁自重，在张拉开始的很长一段时期，加劲梁基本不会脱离支架，受力也变化不大，而随着吊杆的不断张拉，加劲梁一旦脱离支架实现体系转换后，每张拉一步，加劲梁的变形和受力状态都会发生较大变化；由于张拉前采用大节段吊装架设、简支变连续方式施工，加劲梁在临时墩支架上处于简支受力的连续状态，从而导致在吊杆张拉过程中加劲梁变形不均匀，在大节段跨中变形较大，支点变形较小，因此加劲梁在工厂拼装施工时预拱度设置要求较高；在整个吊杆张拉过程中，边跨最大变形为30 cm左右，在加劲梁整体弯矩逐渐增大的情况下，主缆在梁上锚固从而传递给加劲梁的轴向压力也逐渐增大，钢加劲梁处于较为安全的压弯状态，应力储备较大。

8 支点反力响应

吊杆张拉过程中加劲梁与支架之间的相互作用力的变化是非线性的。最初，加劲梁的自重完全由临时支架承担，随着吊杆的不断张拉，加劲梁与支架之间逐渐脱离且实现体系转换。支架只承受压力，不承受拉力，加劲梁和支架之间存在只压不拉的接触非线性关系。

永久支座同样有一定的承载力要求，在吊杆张拉过程中，吊杆张拉和临时支架的拆除都会引起永久支座反力的变化。因此吊杆张拉方案必须保证永久支座的安全，且不能出现负反力，需布置压重以保证支座受力安全。

按上述方案对吊杆张拉过程中的支点反力进行分析计算，各步骤临时和永久支座反力如图10、11所示。

图10 各步骤11#临时支座反力

图11 各步骤永久支座反力

通过计算分析可知，自锚式悬索桥在吊杆张拉过程中的支点反力主要变化规律如下：在吊杆张拉过程中，加劲梁逐渐脱离支架从而实现体系转换，临时支撑完全脱离，而永久支撑完全受力；临时支架支撑反力总体逐渐减小，但在某些张拉步骤会出现增大现象，应保证支点承载力及加劲梁局部加强构造受力不能超限，临时支撑一旦脱离应立即拆除，防止某些阶段梁体重新回落造成支撑偏离；由于主缆竖向分力及吊杆力逐渐增大和临时支撑的逐渐拆除，永久支座反力也不停地发生变化，在保证其承载力满足要求的前提下，也要防止负反力的出现，因此应在张拉的合理阶段逐渐施加压重，保证支座受力在一定安全范围。

9 结 语

在吊杆张拉的体系转换过程中，空间索面自锚式悬索桥由于主缆、吊杆、加劲梁及索塔等多参数高度耦合，体系转换过程中结构响应更为复杂，本文通过有限元手段，对吊杆张拉过程中主缆的大位移非线性、吊杆索力的相干性、索塔的变位和受力、加劲梁的变形和受力、永久和临时支点的反力变化等结构响应规律进行研究，主要结论如下。

(1)主缆呈现出显著的大位移非线性特点；每步张拉中张拉点位移变化较大，附近点位移逐渐减小，同跨远离张拉点的部分点出现明显的反向位移；在后续吊杆张拉过程中，张拉过的节点位移基本不再发生较大变化。

(2)开始张拉时主缆刚度较小，吊杆可以一步张拉到位，但在逐渐张拉过程中主缆刚度逐渐增大，部分吊杆需多次张拉才能张拉到位；吊杆力在张拉过程中变化较大，最大索力和最小索力均需满足一定安全系数；张拉吊杆导致附近已张拉点索力出现明显卸载现象，而远离张拉点索力及邻跨索力却出现增大现象。

(3)索塔在吊杆张拉前的空缆状态处于平衡，在张拉过程中主缆水平分力不再平衡，需进行索鞍顶推以保证索塔受力安全；索鞍顶推会造成索塔位移和应力出现急剧变化，因此应尽早顶推且顶推次数越少越好；成桥状态的索鞍已顶推至索塔中心，索塔恢复平衡受力状态。

(4)在吊杆张拉开始的很长一段时期，加劲梁基本不会脱离支架，随着吊杆的不断张拉，加劲梁一旦脱离支架实现体系转换，后期每一步张拉都将引起加劲梁变形和受力的较大变化；整个张拉过程中加劲梁基本处于较为安全的压弯状态，但加劲梁线形特点对其预拱度设置提出了较高的要求。

(5)在吊杆张拉过程中，加劲梁逐渐脱离支架从而实现体系转换，临时支撑完全脱离，而永久支撑完全受力；临时支架支撑反力在某些张拉步骤会出现增大现象，应保证支点承载力及加劲梁局部加强构造受力不能超限；永久支座反力应保证其承载力满足要求，必要时应在合理阶段逐渐施加压重防止负反力的出现。

[1] 邱文亮，张 哲.自锚式悬索桥施工中的吊杆张拉方法研究[J].大连理工大学学报，2007，47(4)：532-536.

[2] 罗 实.自锚式悬索桥吊杆力调整过程研究[D].成都：西南交通大学，2008.

[3] 刘小飞.自锚式悬索桥吊杆张拉计算和有限元分析研究[D].成都：西南交通大学，2006.

[4] 李照众.自锚式悬索桥吊杆张拉计算及施工控制分析[D].南京：南京林业大学，2009.

[5] 邢 智.自锚式悬索桥吊杆张拉过程优化分析[D].西安：长安大学，2009.

[6] 柯红军，李传习，张玉平.双塔大横向倾角空间主缆自锚式悬索桥体系转换方案与控制方法[J].土木工程学报，2010，43(11):94-101.

[7] 牛登辉，周志祥，吴海军.自锚式悬索桥体系转换过程的无应力状态控制法[J].重庆交通大学学报:自然科学版，2014，33(1):21-24.

[8] 张俊平，黄海云，刘爱荣，等.空间缆索自锚式悬索桥体系转换过程中受力行为的全桥模型试验研究[J].土木工程学报， 2011，44(2):108-115.

[9] 沈锐利，齐东春，唐茂林.杭州江东大桥静力特性全桥模型试验研究[J].土木工程学报，2011，44(1):74-80.

[10] 胡建华，沈锐利，张贵明，等.佛山平胜大全全桥模型试验研究[J].土木工程学报，2007，40(5):17-25.

[11] 王 桢.超大跨径自锚式悬索桥几何非线性行为理论与试验性能研究[D].重庆:重庆交通大学，2013.

[12] 李传习.混合梁悬索桥非线性精细计算理论研究[D].长沙：湖南大学，2006.

[13] 邱文亮.自锚式悬索桥非线性分析与试验研究[D].大连：大连理工大学，2004.

[14] 李传习，柯红军，刘 建，等.平胜大桥体系转换施工控制的关键技术[J].土木工程学报，2008，41(4):49-54.

[15] 李传习，柯红军，杨 武，等.黄河桃花峪自锚式悬索桥体系转换方案的比较研究[J].土木工程学报，2014，47(9):120-127.

[16] 王邵锐，周志祥，吴海军.超大跨自锚式悬索桥施工过程中力学性能的试验研究[J].土木工程学报，2014，47(6):70-77.

[17] 杨孟刚， 陈政清.自锚式悬索桥施工过程模拟分析[J].湖南大学学报：自然科学版，2006，33(2):26-30.

StructuralResponseofBoomTensioningProcessofSelf-anchoredSuspensionBridge

HUANG Shao-hua1, WEI Jia-le2

(1. Second Engineering Company of CCCC Tunnel Engineering Co., Ltd., Xi’an 710100, Shaanxi, China;2. Shaanxi Tongyu Highway Research Institute Co., Ltd., Xi’an 710100, Shaanxi, China)

Aiming at the troublesome process, the difficulty of construction control and the complex structural response during the boom tensioning of self-anchored suspension bridge, the finite element model of a self-anchored suspension bridge with spatial cables was established, and a reasonable tension control scheme was put forward. The results show that the main cable exhibits a significant displacement nonlinearity during the lifting process of the boom; the coherence between the booms is noticeable and complex; a reasonable saddle thrust is needed to ensure the stress state of the cable tower; the stiffened beams are gradually separated from the brackets and achieve system conversion; the reaction force of the temporary and permanent supports changes significantly.

self-anchored suspension bridge; structural response; finite element analysis; boom tensioning

U442.5

B

1000-033X(2017)11-0118-08

2017-03-27

黄少华(1975-)，男，湖北潜江人，高级工程师，工程硕士，研究方向为桥梁与隧道施工。

[责任编辑:高甜]