渗流-应力耦合作用下砂岩声发射及分形损伤特征研究

付小凤

(重庆水利电力职业技术学院，重庆 402160)

渗流-应力耦合作用下砂岩声发射及分形损伤特征研究

付小凤

(重庆水利电力职业技术学院，重庆 402160)

为探究渗流-应力耦合作用下岩石内部微元体的损伤演化特征，对取自某矿井的砂岩进行了三轴渗透及声发射试验。研究结果表明：砂岩的渗透率变化历经降低、动态平衡、快速增加以及略微回落四个阶段；声发射现象呈阶段性变化特征，随着围压的升高，声发射最大值越滞后；基于柱状分形理论得到的分形特征表明，分形维数逐渐降低，表明砂岩内部损伤经历了一个从无序到有序的变化趋势，分形维数突变点的出现，可作为砂岩即将失稳破坏的前兆；渗流-应力耦合作用下砂岩的损伤值呈指数型函数增加，渗透损伤Ds主要集中于屈服阶段之后，渗透损伤与总损伤的比值随围压的升高呈线性减小；应力加载是损伤产生的主要因素，渗透作用为次要因素；分形维数df与损伤D、渗透损伤Ds之间呈良好的负指数型函数关系。

渗流-应力耦合作用；砂岩；声发射；分形；损伤

砂岩是现代矿山、交通、水利、油气田等工程中最为常见的岩石之一，其力学性质一直受到众多专家学者的关注，尤其是渗透特性，对工程的安全和稳定起着十分重要的影响，因而研究砂岩渗流-应力耦合作用下的力学行为对预防工程地质灾害具有重要意义。杨建等[1]对松散砂粒孔隙结构、孔隙分形特征及渗透率进行了研究，认为利用孔隙结构特征参数和分维数，可以计算得到砂岩的渗透率；王小江等[2]利用三轴耦合试验机进行粗粒砂岩不同围压条件下变形破坏过程的渗流试验，分析了粗粒砂岩变形破坏过程中渗透性变化规律和围压对于粗粒砂岩渗透性质的影响，通过理论推导了渗透系数与体积应变的关系；Li 等[3]对殷庄砂岩展开了不同围压、孔压和试样尺寸下渗透规律的影响研究，认为渗透率、轴向应力和应变之间具有明显的函数关系。张渊等[4]分析探讨了温度和孔隙压力对细砂岩渗透率的影响规律，认为渗透率同时存在门槛值温度和孔隙压力门槛值；孔茜等[5]对砂岩在加卸载条件下孔隙度与渗透率的关系进行了研究，发现在围压加载阶段，孔隙度和渗透率之间呈指数关系，而在卸载阶段时，两者之间则呈幂函数关系。

声发射是用于监测研究岩石类材料内部损伤的可靠手段之一，逐渐被广泛应用于各类工程当中。王璐等[6]分析探讨了砂岩变形破坏过程中的渗透特性及声发射特性，指出横向变形增加的突变点与渗透率的突变点相对应，其更能反映渗透性的变化。俞缙等[7]对红砂岩进行了常规加载、峰前和峰后卸围压3种应力路径下的气体渗透三轴试验和声发射监测，指出渗透率、声发射、应力和体应变之间存在一定对应关系。本文在以上研究基础上，对砂岩开展了三轴应力状态下的渗透声发射试验研究，并基于柱状分形理论[8]和weibull损伤分布函数[9]对砂岩在渗流-压力两相耦合作用下的分形损伤特征进行了研究。

1 试验样品和方案简介

试验样品取自某矿井地下约600～650 m深处，为灰黑色中等颗粒砂岩，主要成分为石英、长石、方解石、泥质胶结物等。将现场取回的岩芯按《工程岩体试验方法标(GB/T50266—99)》[10]通过钻、切、磨的方法加工制成直径为50 mm、高为100 mm的标准圆柱形试件。试验共设4个围压，分别为5，10，15，20 MPa；渗透测试过程中对试件施加的初始压差为1 MPa，渗透过程中保持围压不变，全程共进行了7次渗透测试，峰前、峰值以及峰后各4次、1次和2次；声发射通道共8个，上下两端各对称均匀分布4个，声发射门槛值大小均设置为45 dB。

2 试验结果分析

2.1应力-应变特征

试验得到渗流-应力耦合作用下的应力-应变曲线(图1)，其中，σ1、σ3、ε1、ε3、εv分别表示主应力、围压、轴向应变、横向应变以及体积应变。从图中可以看到，砂岩的强度随围压升高而增大，破坏方式逐渐由脆性向脆延性转变，各应变值也相应增大。从整体上来看，砂岩的应力-应变可分为四个阶段：短暂的压密阶段、弹性阶段、塑性变形阶段以及峰后残余变形阶段。

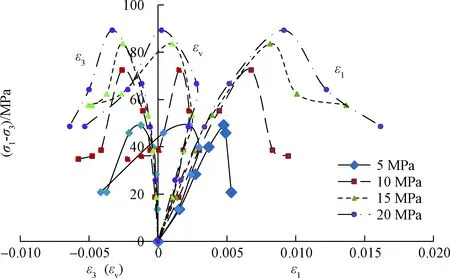
图1 渗流-应力耦合作用下应力-应变曲线特征Fig.1 Characteristics of stress-strain curves under the coupling of seepage and stress

2.2渗透率特征

岩石材料的体积变形在一定程度上反映了试件内部随应力-应变发展变化过程中，硬化及软化相互之间的转变情况[11]，即能够反映其内部损伤发展的情况。不同围压下，渗透率、体积应变与轴向应变的关系(图2)表明，砂岩的体积变形随轴向应变的增加呈先增加后减小的趋势，即经历了从体积压缩到体积膨胀的过程，而渗透率k则经过了“降-平衡-升-降”四个不同阶段的变化。在压密及弹性变形阶段，砂岩呈现出自我调整至原位状态的趋势，原始裂纹及新生裂纹在荷载作用下会被迅速压密闭合，试件各项力学性质有所增强，即压缩硬化过程，因而渗透率逐渐减小并趋于稳定。当砂岩进入屈服塑性变形后，岩石逐渐由硬化压缩过程转入剪胀损伤过程，此时有序裂隙的衍生、发展和贯通逐渐处于主导地位，岩石力学性质开始劣化，渗透系数快速增大，并在峰值应力附近达到最大值，试件内部形成宏观破裂面，岩石发生失稳破坏。峰后残余变形阶段，砂岩进入软化剪胀损伤过程，体积快速膨胀，但渗透率略有回落，这是因为峰后阶段，砂岩试件内部的应力会重新分布，在屈服阶段产生的部分裂纹和裂隙在应力作用下又被重新压密闭实，而砂岩破坏时产生的部分碎屑、泥质颗粒等杂质会附着在渗透通道中，对渗流通道造成堵塞。同时在峰后阶段应力加载方式改为应变控制，轴向应力在改变控制方式后会出现松弛现象，从而使试件内部裂纹的扩展速度变缓，渗透率也随之略有回落。

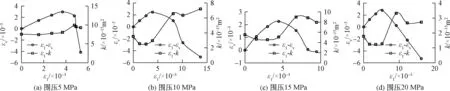
图2 渗透率、体积应变与轴向应变关系Fig.2 Relationship between permeability, volume strain and axial strain

2.3声发射特征

能够准确反映试件内部损伤演化的声发射参数为振铃计数率[12～13]，因而本文对声发射振铃计数与应力-应变的关系进行分析和探讨(图3)。从整体上来看，振铃计数率在应力加载阶段较为活跃，在渗透测试阶段则比较平静，这是因为在压密阶段，砂岩原始微孔隙、微裂隙被压密，颗粒之间产生摩擦信号较多，声发射较活跃。弹性阶段主要是原始微裂纹微裂隙发生闭合，没有新的损伤形成，渗流通道连通性较差，因此岩石的渗透性很小，声发射信号也较弱；塑性变形阶段，新的裂纹不断萌生、发展和贯通，对应的渗透率快速增加，渗透测试过程中的声发射信号显著增强。峰后残余阶段，声发射整体信号在渗透测试过程中略有降低，这主要是由于砂岩内应力调整，裂隙发展速度变缓，渗透率稍有降低，声发射信号略有回落。因而声发射信号在整个测试过程中呈“减小-平衡-增大-回落”的变化趋势，这与渗透率变化趋势保持一致。随着围压的升高，声发射振铃计数率最大值(最活跃处)从峰值应力阶段逐渐向峰后阶段转移，表明了围压对声发射的影响：侧向应力值越大，试件的声发射现象(最大值)越滞后，这是因为在高围压作用下，岩石逐渐从脆性向塑性破坏转变，且在低围压下，AE信号主要由内部微裂纹贯通及破坏面晶粒间滑移产生并稍有增强，而在高围压下，AE信号则主要是由晶粒的位错重组引起，因而会出现声发射信号的滞后现象。

图3 振铃计数与应力-应变关系Fig.3 Relationship between stress-strain and counting

2.4基于声发射的分形及损伤特征

2.4.1分形及损伤理论

岩石的损伤主要是由其内部的微孔隙、微裂纹的不规则产生和扩展造成的，但却具有统计自相似性[14]。为了描述自然界存在的不规整现象，Mandelbrot于1982年提出了分形几何学，经过多年的演变发展，已被广泛应用于岩石类材料的损伤研究当中。与之相对应的还有损伤力学的发展，其直接反映了岩石内部力学性质劣化程度的大小。基于声发射参数，可分别得到砂岩渗透作用下的分形与损伤演化规律以及两者之间的相互关系。

(1)柱状分形理论。目前比较常用的分形方法为投影法和覆盖法。基于本次试验试件均为圆柱形，因此，本文采用柱状分形法对砂岩渗流应力耦合下的分形特征进行分析和探讨。该理论认为：每一个半径和高度对应体积下的试件均可对应于一个声发射事件总数M(ri)，随着半径和高度的增加，其对应的声发射事件总数在不断变化。在某一时间点，若取多个半径对应下的事件总数，就能通过半径和声发射事件数进行线性拟合，这个线性拟合斜率即表示这个时刻试件的df值。根据该分形理论的定义，可用如下关系式来表示声发射事件点与空间圆柱半径r的关系[8]：

将上式两边同时取对数即可得：

式中：C——与声发射事件数和半径相关的拟合常数；

df——所求的分形维数，且2≤df≤3。

(2)Weibull损伤方程。假定岩石类材料微元强度服从Weibull函数分布的统计规律[15]，即有：

损伤本构模型即为：

式中：Nm——完全破坏时声发射振铃累计数；

N——当前声发射振铃累计数；

ε0——力学参数，本文取应变进行计算；

m——与材料均质性有关的形态参数；

D——损伤变量。

2.4.2分形与损伤演化特征

利用时空序列关系，采取相应的计算方法，将声发射的原始空间事件点进行还原处理，得到了不同围岩情况下分形维数随应力-应变关系的变化特征(图4)。从图中可以看到，在渗流-应力环境下砂岩的分形维数变化特征表现一致，均呈现为逐渐减小的过程，即表明砂岩在渗透损伤过程中历经从无序到有序的变化特征。压密及弹性阶段，声发射信号主要以原始随机分布微裂纹和微裂隙的闭合为主，因而产生比较离散的声发射信号，所以分形维数呈现较大值；在砂岩的塑性变形期，试件内部会产生大量新生裂纹并沿着这些新生裂纹逐渐发展，形成一道道有序而规则的连通面，再次过程中伴随着声发射的产生并集中于破裂面附近，因而分形维数会显著降低；当砂岩破坏后，裂纹的扩展速度则会相对变缓，从而使得分形维数的变化相对较小。砂岩在达到峰值应力之前，分形维数均会有一个比较大的降幅，这可以被认为是砂岩即将失稳破坏的前兆。

图4 df随应力-应变的变化趋势Fig.4 Change trend of df with stress strain

通过式(3)、(4)拟合计算得到了整个试验过程中损伤与应变的关系(图5)。从图中可以看到，损伤随着应变的发展呈指数型函数变化，不同围压下的砂岩均会存在一个渗透损伤阈值，当损伤量超过这一特定阈值后，损伤便会快速增长，表明此时砂岩内部的力学性质已经开始发生实质性的劣化。

图5 各围压下损伤与应变的关系Fig.5 Relationship between damage and strain under confining pressure

不同围压下砂岩的渗透损伤Ds的累计值见图6。可以看到：随着渗透试验的进行，Ds累计值表现为幂函数变化关系，渗流-应力作用下，砂岩内部力学性质逐渐劣化，水的软化作用在一定程度上又降低了试件内部颗粒之间的相互胶结力，因而加大了损伤的发展速度；渗透损伤随着围压的升高而减小，表明侧向约束力的存在在一定程度上会延缓砂岩的渗透损伤发展。

图7为试验砂岩Ds/D比值与围岩的变化关系，可以看到，Ds/D与围岩基本呈线性减小关系，且其值大概在10%～15%之间，再次表明围压对渗透损伤发展的抑制作用，围压的增大可以使因渗透作用产生的损伤量越小。

图6 Ds累计值变化趋势Fig.6 Change trend of Ds cumulative value

图7 渗透损伤比重与围压的关系Fig.7 Relationship between the percentage of permeability damage and confining pressure

上文分析得到了不同侧向约束力下砂岩渗透全过程的分形与损伤的演化规律，根据两者的拟合计算结果，得到了分形维数df与损伤D以及渗透损伤Ds的相互关系(图8)。从图中可以看到，分形维数与损伤(D、Ds)之间呈良好的负指数型函数关系。这是因为加载初期，砂岩内部损伤较小，新生微裂纹、微裂隙以随机无规则的方式产生，而随着应力的增加，损伤越来越大，此时，裂纹之间相互贯通，逐渐朝有序化发展，因而分形维数越小。

图8 分形维数df与损伤D/Ds之间的关系Fig.8 Relationship between fractal dimension df and D/Ds

3 结论

(1)砂岩的渗透率随应力呈明显的“降-平衡-升-降”的阶段变化特征，与之相对应的声发射现象也呈阶段性的变化趋势；围压值越大，声发射振铃计数最大值越滞后。

(2)分形维数随着应力加载呈逐渐降低趋势，表明砂岩内部的损伤演化过程是从无序到有序变化的，分形维数突降阶段的出现预示着砂岩内部即将发生失稳破坏。

(3)基于weibull损伤分布函数的结果表明，渗流-应力耦合作用下砂岩的损伤值呈指数型函数增加，渗透损伤Ds主要集中于屈服阶段之后；应力加载是岩石内部损伤的主要因素，渗透损伤为次要因素；分形维数df与损伤D、渗透损伤Ds之间呈良好的负指数型函数关系。

[1] 杨建, 陈家军, 杨周喜,等. 松散砂粒孔隙结构、孔隙分形特征及渗透率研究[J]. 水文地质工程地质, 2008, 35(3):93-98. [YANG J, CHEN J J, YANG Z X,etal. A study of pore structure , pore fractal feature and permeability of unconsolidated sand [J]. Hydrogeology amp; Engineering Geology, 2008, 35(3):93-98. (in Chinese)]

[2] 王小江, 荣冠, 周创兵. 粗砂岩变形破坏过程中渗透性试验研究[J]. 岩石力学与工程学报, 2012, 31(A01): 2940-2947. [WANG X J, RONG G, ZHOU C B. Permeability experimental study of gritstone in deformation and failure processes[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31 (A01): 2940-2947. (in Chinese)]

[3] LI S P，WU D X，XIE W H，etal. Effect of confining pressure，pore pressure and specimen dimension on permeability of Yinzhuang sandstone[J]. International Journal of Rock Mechanics and Mining Sciences，1997，34(3/4)：175.

[4] 张渊，赵阳升，万志军，等. 不同温度条件下孔隙压力对长石细砂岩渗透率影响试验研究[J]. 岩石力学与工程学报，2008,27(1)：53-58.[ZHANG Y, ZHAO Y S, WAN Z J,etal. Experimental study on effect of pore pressure on feldspar fine sandstone permeability under different temperatures [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27 (1): 53-58. (in Chinese)]

[5] 孔茜，王环玲，徐卫亚. 循环加卸载作用下砂岩孔隙度与渗透率演化规律试验研究[J]. 岩土工程学报，2015, 37(10)：1893-1900. [KONG Q, WANG H L, XU W Y. Experimental study on permeability and porosity evolution of sandstone under cyclic loading and unloading [J]. Chinese Journal of Geotechnical Engineering, 2015,37 (10): 1893-1900. (in Chinese)]

[6] 王璐，刘建锋，裴建良，等. 细砂岩破坏全过程渗透性与声发射特征试验研究[J]. 岩石力学与工程学报，2015，34(增刊1)：2909-2914. [WANG L, LIU J F, PEI J L,etal. Experimental research on permeability and acoustic emission characteristics during whole failure process of fine sandstone [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34 (Sup1): 2909-2914. (in Chinese)]

[7] 俞缙，李宏，陈旭，等. 砂岩卸围压变形过程中渗透特性与声发射试验研究[J]. 岩石力学与工程学报，2014，33(1)：69-79. [YU J, LI H, CHEN X,etal. Experimental study of permeability and acoustic emission characteristics of sandstone during processes of unloading confining pressure and deformation [J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33 (1):69-79. (in Chinese)]

[8] Xie H P，Liu J F，Ju Y，etal. Fractal property of spatial distribution of acoustic emissions during tHe failure process of bedded rock salt[J]. Int J Rock MecH Min Sci，2011:1215-1382.

[9] 唐春安. 岩石破裂过程中的灾变[M]. 北京：煤炭工业出版社，1993. [TANG C A. In the process of rock fracture disaster [M]. Beijing: Coal Industry Press, 1993. (in Chinese)]

[10] GB/T50266—99 工程岩体试验方法标准[S]. 1999. [GB/T50266—99 Engineering rock mass test method standard [S]. 1999. (in Chinese)]

[11] 陈宗基, 康文法, 黄杰藩. 岩石的封闭应力. 蠕变和扩容及本构方程[J]. 岩石力学与工程学报, 1991, 10(4): 299-312.[CHEN Z J, KANG W F, HUANG J F. On the locked in stress, creep and dilatation of rocks, and the constitutive equation[J].Chinese Journal of Rock Mechanics and Engineering, 1991, 10 (4): 299-312. (in Chinese)]

[12] HEIPLE C R, CARPENTER S H. Acoustic Emission from Dislocation Motion[M].New York: Gordon and Breach Science Publishers,1983

[13] WADLEY HNG, SCRUBY C B, SPEAKE J H. Acoustic emission for physical examination ofmetals[J]. International Metals Reviews,1980, 25(1):41-64.

[14] Mendelbrot B B.The Fractal Geometry of Nature[M]. New York: W H Freeman, 1982:895-930.

[15] 熊雪强. 分级循环加卸载砂岩蠕变声发射特性研究[D]. 南昌:江西理工大学, 2012. [XIONG X Q. Study on acoustic emission characteristics of compacted sandstone classification of cyclic loading and unloading [D].Nanchang: Jiangxi University of Science and Technology, 2012. (in Chinese)]

责任编辑

：汪美华

Astudyoftheacousticemissionandfractaldamageofsandstoneunderthecouplingofseepageandstress

FU Xiaofeng

(ChongqingWaterResourcesandElectricEngineeringCollege,Chongqing402160,China)

Mechanical properties of rock under seepage-stress coupling are important in mine engineering. In order to explore the evolution of the internal micro-hydro rock damage force under coupling of mine engineering from a sandstone, three axial penetration and acoustic emission tests are conducted. The results show that the change in permeability of the sandstone includes four stages: decrease, dynamic balance, rapid increase and slight decline. The acoustic emission phenomenon is characterized by a periodic change, and the greater the confining pressure is, the more the acoustic emission is lagged. Fractal characteristics based on the columnar fractal theory show that the fractal dimension decreases gradually. The results also show that the internal damage of the sandstone has experienced a change from disorder to order, and the emergence of the fractal dimension can be used as a precursor to the failure of the sandstone. The damage value of the sandstone under seepage-stress coupling increases exponentially, and the seepage damageDsmainly concentrates on the yield stage. The ratio of the osmotic damage to the total damage decreases linearly with the increasing confining pressure. Stress loading is the main factor of the sandstone damage and the osmotic damage is a secondary factor. The fractal dimensiondfhas a good negative exponential function with the damageDand the osmotic damageDs.

seepage-stress coupling effect; sandstone; acoustic emission; fractal; damage

10.16030/j.cnki.issn.1000-3665.2017.06.13

TU458+.3

A

1000-3665(2017)06-0083-06

2016-11-14;

2017-03-10

校级科研项目(K201522)

付小凤(1982-)，女，硕士，讲师，一级建造师(建筑工程)，主要研究方向为项目管理、工程造价、岩土工程。

E-mail: eeptuuy4360347@163.com