不同厚度溶洞顶板与基桩作用机理室内模型试验研究

赵明华，吴高桥，肖 尧，杨超炜，徐卓君

(湖南大学岩土工程研究所，湖南 长沙 410082)

不同厚度溶洞顶板与基桩作用机理室内模型试验研究

赵明华，吴高桥，肖 尧，杨超炜，徐卓君

(湖南大学岩土工程研究所，湖南 长沙 410082)

根据相似理论，设计了3组不同厚度条件下溶洞顶板破坏模式的大比例模型试验，得到了顶板和基桩的荷载-位移曲线、顶板底部的极限应变曲线和不同厚度条件下溶洞顶板的破坏特性。试验结果表明：当溶洞顶板厚度为1d，2d时，发生冲切破坏，冲切体为圆台；当溶洞顶板厚度为3d时，顶板则以弯拉破坏为主，无冲切体产生。在荷载-位移曲线中，线性阶段转变为非线性阶段的临界点约为极限承载力的一半。最后通过理论计算的方法，获得溶洞顶板最小安全厚度计算公式，分析结果与试验结果吻合较好，能满足工程计算精度要求。本文试验成果是基于工程最不利情况得出的，可供岩溶区基桩初步设计参考。

顶板破坏模式；溶洞；模型试验；安全厚度

近年来，在我国西部地区建设工程中频繁地受到岩溶地质的不利影响，部分桥梁、码头桩基坐落在溶洞顶板上，若设计不当会严重阻碍施工进度甚至危及工程安全。因此有必要开展岩溶区溶洞顶板承载机理以及基桩、溶洞的相互作用关系研究。

为此，国内外学者从理论研究、数值研究和试验研究三方面探讨了岩溶区顶板承载机理及最小安全厚度确定方法。理论研究方面，赵明华等[1～2]建立了桩端岩层抗剪、抗冲和抗弯的计算模型，推导出考虑冲切台自重的溶洞顶板最小安全厚度计算公式；此后，雷勇等[3]基于Hoek-Brown岩石破坏判据，对溶洞顶板的冲切破坏进行了更深入的研究；龚先兵等[4]虑溶到洞顶板破坏时的突发特点，引入突变理论，对岩溶区嵌岩桩桩端极限承载力进行了研究；Jiang等[5]结合弹性力学方法，得出考虑嵌岩段岩层与溶洞顶板之整体承载效应的溶洞顶板极限承载力计算公式。数值分析方面，黎斌等[6]采用三维有限元法对嵌岩桩桩端荷载作用下溶洞顶板的稳定性进行了分析；孙映霞等[7]采用有限差分法对基桩作用下的溶洞破坏机制进行了分析；尹凯丽等[8]采用ANSYS有限元软件探究了不同影响因素对桩基极限承载力的影响。试验研究方面，Menetrey等[9]通过数值模拟和模型试验，研究了顶板抗拉强度对冲切破坏的影响，得出厚板冲切破坏模型；刘铁雄等[10～11]基于相似原理，对岩溶区顶板的作用机理及顶板和基桩的承载特性开展了室内比例模型试验研究，并详细说明了室内比例试验的模拟尺寸、模拟材料及其试验方案；张慧乐等[12～13]基于以上试验，对岩溶区基桩的承载能力和破坏模式进行了室内试验研究，结果表明，岩溶区基桩的桩端承载力及其破坏模式与溶洞的位置和形状有关。以上试验研究为本文室内试验提供了参考依据。

在实际工程中，溶洞形状的不确定性、岩石材料的非线性以及基桩承载机理的复杂性，使得岩溶区基桩与溶洞的相互作用更为复杂。现有研究对岩溶区基桩与溶洞的相互关系并未研究透彻，为确保工程安全，本文将溶洞顶板简化为梁板结构来考虑，基于以上研究和相似原理[15]，拟开展3组试验，重点研究不同厚度条件下溶洞顶板与基桩的破坏模式及溶洞顶板的承载能力，并对试验所得的荷载-位移曲线、荷载-应变曲线、顶板破坏形式以及顶板破坏后的冲切体形态进行对比分析，得出溶洞顶板最小安全厚度，并将依据顶板最小安全厚度公式推导的结果与试验结果进行对比，以期获得更符合实际情况的溶洞顶板承载力的计算公式。

1 试验设计与方法

1.1模型试验概况

本试验是在湖南大学岩土实验室地槽内完成，如图1所示。支座由混凝土浇筑而成，溶洞顶板模型试验设计如图2所示。

图1 实验室地槽Fig.1 Diagram of the geosyncline

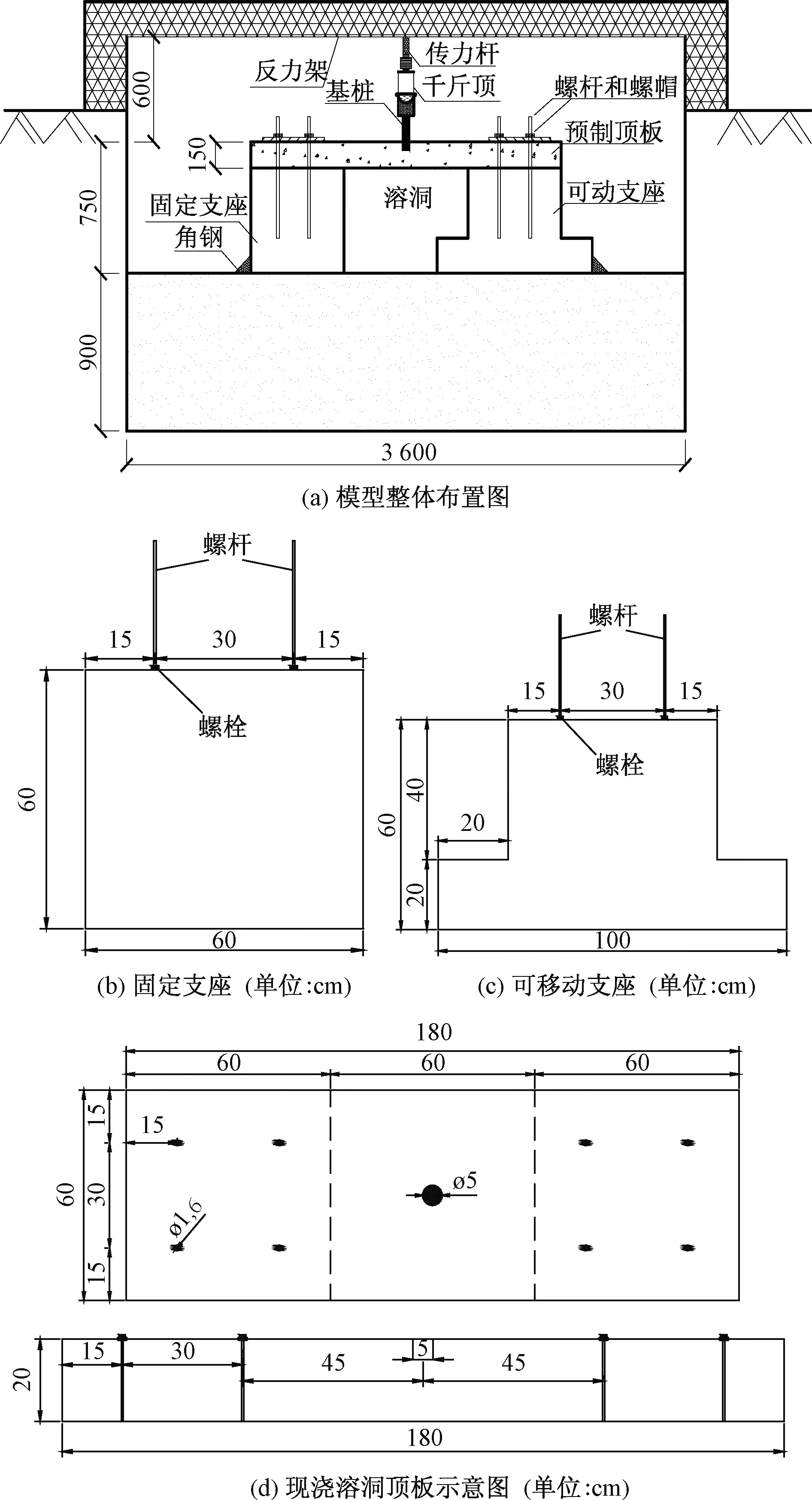
图2 试验模型图Fig.2 Diagram of the test model

1.2试验设计

本次试验主要研究不同顶板厚度条件下的岩溶区基桩桩端承载特性和顶板破坏模式。

试验基桩桩长l=200 mm，其中嵌入板内长50 mm，桩径d=50 mm，顶板宽度600 mm。由于试验着重探究溶洞顶板的破坏模式和承载能力，应尽量缩小桩体本身对于数据的影响。因此选用刚度远大于溶洞顶板的实心钢桩，以保证溶洞顶板先于桩体破坏；其次实心钢桩表面光滑，与岩体模拟材料之间的摩阻力可忽略不计，这样千斤顶施加的荷载即可视为桩端荷载大小。

图3 桩身模拟材料Fig.3 Simulation material of pile

(1)相似原理

根据相似定理可知试验应力相似比表达式为：

式中：(σX)p，(σY)p——原型X，Y方向的正应力；

(τXY)p——原型的剪应力；

(σX)m，(σY)m——模型X，Y方向的正应力；

(τXY)m——模型的剪应力。

几何相似比表达式为：

式中：XP，YP——原型X方向、Y方向的几何长度；

Xm，Ym——模型X方向、Y方向的几何长度。

重度相似比表达式为：

式中：γP——原型材料重度；

γm——模拟材料重度。

将式(1)～(3)代入变形协调方程：

为满足(5)式，通过配合比试验确定该比例试验的重度相似比Cγ为1.3，几何相似比Cl为20，应力相似比Cσ为26。

在厚度试验中选定的水泥砂浆混合料配合比为砂∶水泥∶石膏为5.6∶1∶0.5，水泥选用M32.5水泥。详细指标如表1所示。

表1 厚度试验顶板模拟材料与灰岩力学参数表

(2)边界条件

模型试验顶板简化为两边固定，两边自由板。先按支座的尺寸支模。将支座模板放置于试验场地，测量好预留溶洞顶板的尺寸，依据顶板的尺寸放置支座，然后开始浇筑。支座相对于顶板来说视为刚性基础，故支座材料采用强度较高的C30混凝土，浇筑过程中在固定支座内嵌4根直径φ=16mm的螺栓模拟固支。具体方法如图4所示。

图4 边界条件Fig.4 Boundary conditions

根据顶板对称型，使用辐射式粘贴方式。溶洞顶板上表面粘贴22个应变片，下表面粘贴33个应变片，顶板侧面粘贴11片应变片作为补偿应变片，具体粘贴位置如图5所示。

图5 应变片粘贴位置示意图Fig.5 Strain gauge sticking position of detail

2 试验过程

2.1试验加载系统

本试验采用慢速维持荷载法，竖向分组加载开展破坏性试验。加载设备由加载反力架、液压千斤顶、传力杆等组成(图1)。每级加载不超过8 kN，百分表每5 min读1次，当每级荷载下桩顶位移变化小于0.01 mm/5 min或者累计不超过0.1 mm/h方可进行下一级加载。出现以下情况之一，则终止加载：(1)基桩竖向位移超过0.15倍桩径；(2)顶板发生脆性破坏或坍塌；(3)某级荷载桩顶位移大于前一级荷载的2倍。

加载时，通过百分表读数，可绘制荷载-位移曲线。通过顶板底面应变数据，得到荷载-应变曲线。对以上受力变形情况进行记录，以此分析顶板变形性状和破坏机理。具体加载数据如表2所示。

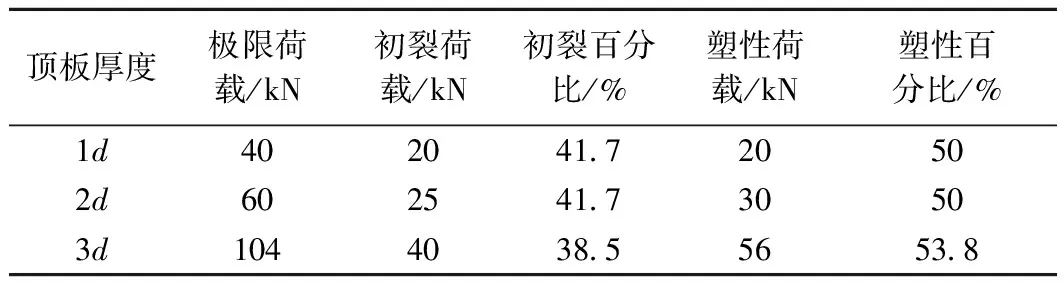
表2 试验加载数据

2.2厚度试验破坏过程

顶板厚度为1d时，顶板发生冲切破坏，A点周围的应变首先溢出，顶板形成细微裂纹，随着竖向荷载继续增加，出现BAC裂纹并逐渐连通形成BACD裂纹。此后千斤顶卸载，顶板失去承载能力，继续加载，图 6所示冲切体被冲出，底面半径为13.8 cm。

图6 h=1d顶板破坏模式Fig.6 Roof failure mode with h=1d

顶板厚度为2d时，顶板发生冲切和弯拉组合的破坏模式，冲切体为半圆台，半径13.6 cm。顶板破坏过程中A，B两点周围最先出现微小裂纹，这时内部冲切体基本形成。随着千斤顶的加载，D，E两点间的细小裂纹先于DBCAE裂纹产生，DE裂纹的形成使得顶板产生较大的挠度，紧接着就出现位于支座边缘处顶板上FG和HI两条连通裂纹，然后继续加载直至冲切体冲出(图7)。顶板厚度增加到3d，顶板破坏模式变为整体弯拉破坏。顶板在加载过程中呈现弹塑性破坏特性，随荷载增大，顶板发生无征兆的瞬时破坏(图8)。

图7 h=2d顶板破坏模式Fig.7 Roof failure mode with h=2d

图8 h=3d顶板破坏模式Fig.8 Roof failure mode with h=3d

3 试验结果

3.1荷载位移曲线

在加载过程中，通过百分表读取各级荷载下位移并将其绘制成基桩荷载位移曲线(图9)。

图9 基桩荷载位移曲线Fig.9 Load-displacement curve of pile

由图9可知，顶板厚度h=1d、上部荷载小于20 kN时，顶板荷载位移曲线呈现线性特征；荷载由20 kN上升至40 kN之间的荷载位移曲线为非线性阶段，即位移变化较大而承载力增加很小；当上部荷载超过40 kN后，顶板下部开始出现裂纹并失去承载能力。当顶板厚度h=2d、上部荷载小于30 kN时，曲线呈现线性特征；随着荷载继续增加至60 kN，该阶段为非线性阶段；当上部荷载超过60 kN，顶板下部出现裂纹从而失去承载能力。当顶板厚度h=3d、荷载小于56 kN时，荷载传递曲线为线性阶段；随着荷载增至96 kN，整个阶段表现为非线性；而当荷载超过100 kN后溶洞顶板便开始破坏。

不难发现，随着顶板厚度的增加，基桩的桩端承载力增大，厚度为3d的基桩承载力比厚度为1d的基桩承载力大200%。且随顶板厚度的增加，荷载位移曲线呈现出比较明显的非线性特征(其中3d比较明显)。通过对比1d，2d和3d三条有非线性特征的荷载位移曲线可知：当顶板厚度为1d时，线性极限承载力为20 kN，非线性极限承载力为40 kN；顶板厚度为2d时，线性极限承载力为30 kN，非线性极限承载力为60 kN；而顶板厚度为3d时，线性极限承载力为56 kN，非线性承载力极限为104 kN。由此可以推测，岩溶区基桩受荷，线性阶段转变为非线性阶段的转折点约为极限承载力的一半，即非线性极限承载力为线性极限承载力的二倍。

在加载过程中，每加载下一级之前通过百分表记录位移大小，然后绘制顶板中心附近的荷载传递曲线(图10)。

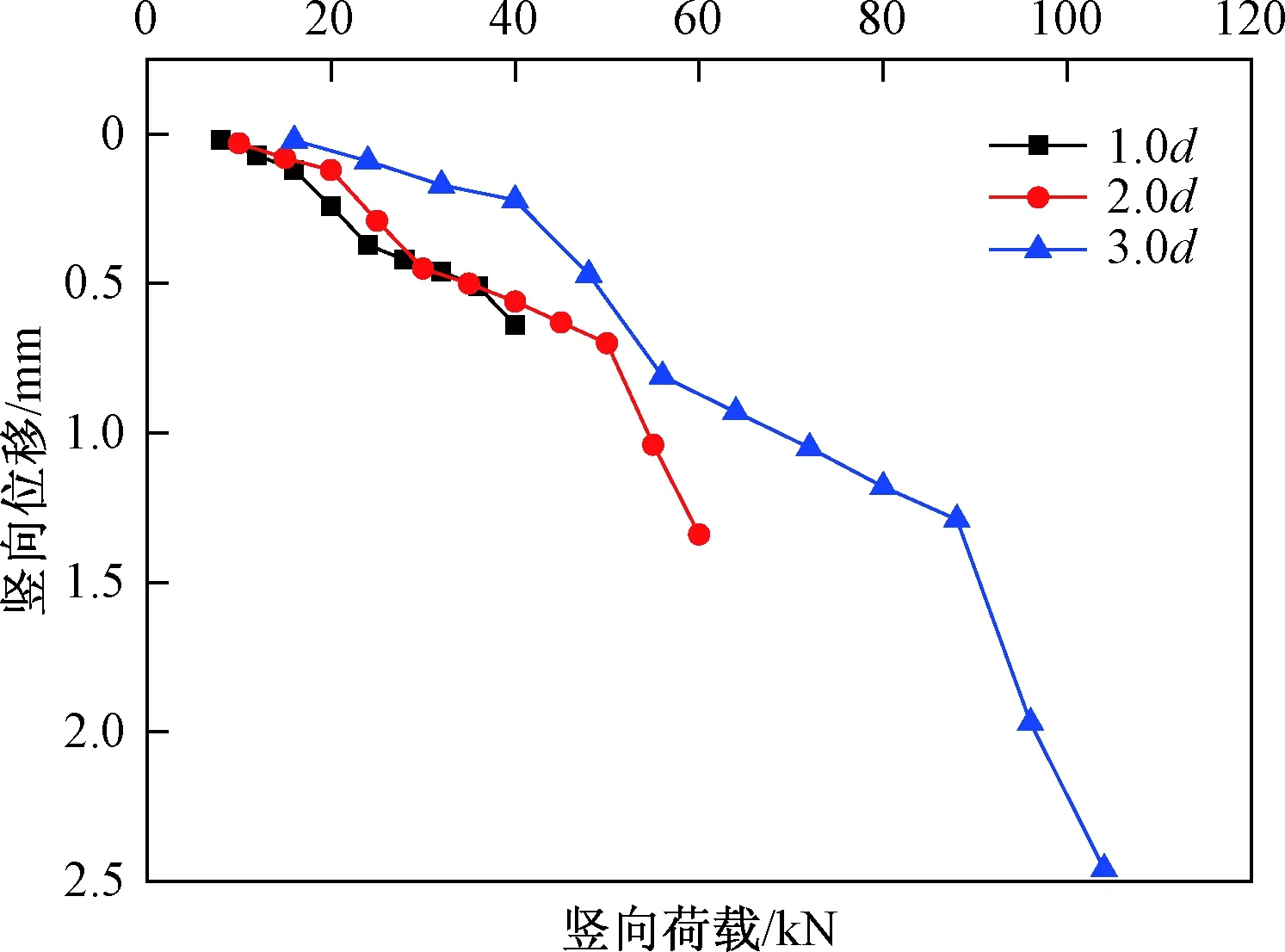
图10 顶板荷载位移曲线Fig.10 Load-displacement curve of the roof

由图10可知，顶板的抗压强度随着顶板厚度的增加而增大。荷载传递曲线呈现非线性特征，试件进入非线性阶段过后都经过一个应变硬化的过程，即曲线先缓后陡，但由于顶板厚度的不同，3d的非线性阶段较1d，2d更为明显。同时由荷载位移曲线可以看出，3个顶板会出现一个比较明显的“阶梯”。即随着荷载逐渐增大，荷载-位移曲线在顶板出现裂缝后，由于错动裂缝被再次压密，顶板和基桩再次咬合，荷载-位移曲线因此经历第二个线性-非线性阶段。

此外，图9、图10之差即钢桩在顶板中的下陷。

3.2顶板极限应变曲线分析

将顶板底面的应变片按图11(a)进行分组，将测量到的极限应变值进行整理，绘出相应的曲线，如图11(b)、(c)、(d)所示。

由极限应变图可知，极限荷载越大的顶板应变越大，且在极限荷载的作用下，顶板中心的应变最大，距顶板中心距离越远，应变越小，且应变减小速度越来越慢，整体呈金字塔状。此外可以发现顶板边缘的应变出现了负值，这是因为顶板变形过程中受到了横向约束，由于板的小挠度变形而产生的薄膜效应在顶板的表面产生了压应力，且越接近支座压应力越大。对比图11(b)、(c)、(d)可以看出，顶板厚度为3d时边缘应变负值较少甚至为正值，而随着顶板厚度的增加，边缘应变负值越来越大，在顶板厚度达到1d时负应变高达-50。这是因为顶板厚度越小，破坏时的挠度越小；顶板厚度越大，破坏时的挠度越大。(以上顶板应变皆由顶板上下平面应变的平均值确定)

由以上分析可以得出结论：顶板挠度越小薄膜受压效应越明显，且越靠近约束处薄膜效应越明显，而挠度较大时薄膜受压效应不明显甚至无压应力产生。

3.3顶板破坏模式分析

试验进行中，顶板失去承载力的瞬间会冲出冲切体。由冲切体的形状可以推测出实验过程中，板内极限荷载影响范围如图12所示。

图11 不同顶板厚度时顶底板部极限应变曲线Fig.11 Curves of ultimate strain of different thickness of the roof

图12 不同顶板厚度时顶板破坏Fig.12 Types of roof failure of different thickness of the roof

当h=1d时，冲切体为圆台，底面半径为13.8 cm，母线呈抛物线，整体剖视图呈屋顶状(图12a)。h=2d时，冲切体依然为圆台，底面半径进一步减小(13.6 cm)，母线与h=1d的圆台相似(图12b)。h=3d时，顶板随着加载发生无征兆的脆性破坏无冲切体产生，通过顶板底面裂纹的走向，以及没有出现冲切锥台进行初步判断，并在图8基础上做了完全破坏试验，顶板厚度为3d完全破坏时与隧道的冒顶破坏类似，中间有一完整核体，由此推测板内荷载影响范围如图12(c)所示。同时，荷载影响区域的母线随着顶板厚度的增大，向中间挤压。h=1d时母线内凹且底面直径为27.6 cm，h=2d时母线内凹幅度更大且底面直径减少为27.2 cm，当顶板厚度增大至h=3d时，母线顶点被压至桩的另一侧且无冲切体形成。由此可得：随着顶板厚度的增加，顶板冲切体随顶板厚度增大而逐渐变小，直至无冲切体产生。

4 溶洞顶板安全厚度确定方法研究

4.1计算模型确定

本文所述的室内厚度试验中顶板为边长60 cm的正方形板，荷载为作用于顶板中央的直径5 cm的圆形均布荷载。荷载作用范围相对顶板很小，同时在中央均布荷载作用下顶板的挠度最大值显然出现在顶板中央而不会出现在顶板边缘。由于研究对象主要是顶板中央位置，而板边缘位置对其影响较小，可忽略不计。

4.2顶板最大挠度计算

一般情况下，常见溶洞顶板的跨度远大于桩径d。并且由试验现象可以看出，顶板变形破坏时的挠度远小于顶板的厚度，因此该问题属于小挠度弯曲问题。

在解答此类问题时，当顶板的挠度w远小于顶板的厚度h，便可认为中面内的应变等于零，从而得出顶板弯曲的基本微分方程为：

式中：w——挠曲线方程；

h——顶板厚度；

q——直径为d的中心圆面积上受均布荷载；

D——顶板的弯曲刚度。

此时，顶板弯矩的表达式为：

对小挠度板，认为薄膜力等于零，即：

由此可得出沿厚度按线性分布的弯曲应力表达式：

式中：E——弹性模量；

z——顶板厚度；

μ——泊松比。

为满足固支板的位移边界条件：

由瑞次法得挠度表达式为：

在式(11)中只取1个待定系数C1，则：

顶板的形变势能U为：

综上得

式中：d——基桩直径；

R——圆形顶板半径。

溶洞顶板弯矩最大的地方发生在r=0处：

由强度第一理论得：

则由第一强度理论推得顶板最小安全厚度的表达式：

根据试验现象，式(20)的适用条件为h≥3d。当hlt;3d时，溶洞顶板发生冲切破坏，可使用文献[7]提供的公式。综上所述，溶洞顶板最小安全厚度可依据式(21)计算：

式中：σt——抗拉强度；

F——桩端承受荷载；

d1——冲切体下部直径。

依据式(21)计算的溶洞顶板最小安全厚度与试验结果对比如表3所示。

表3 溶洞顶板最小安全厚度表

通过比较溶洞顶板最小安全厚度理论计算结果与试验结果可知，溶洞顶板厚度为1d，2d时，基于冲切破坏理论所得溶洞顶板最小安全厚度值与试验结果符合较好；溶洞顶板厚度为3d时，本文推导的溶洞顶板最小安全厚度值与试验结果吻合较好。这与前文所述试验结论一致：随着溶洞顶板厚度的增加，基桩荷载传递曲线呈现出较为明显的非线性阶段(其中3d更为明显)。即顶板厚度为3d时主要呈现弯曲破坏，厚度1d时顶板主要为冲切破坏，顶板厚度在两者之间为弯曲、冲切混合破坏。

5 结论

(1)当溶洞顶板厚度为1d时，顶板呈现弹脆性破坏，并没有显著的非线性破坏特征；当溶洞顶板厚度为3d时，顶板则以弯拉破坏为主，荷载传递曲线呈现明显的非线性特征；而顶板厚度为2d的情况下，溶洞顶板发生冲切破坏和弯拉破坏相结合的破坏模式。

(2)随着顶板厚度的增加，基桩的桩端承载力增大，厚度为3d的基桩承载力比厚度为1d的基桩承载力大2倍之多。且基桩弹性阶段转变为非线性阶段的转折点为极限承载力的一半位置，即非线性极限承载力为线性极限承载力的二倍。 桩端荷载加载过程中，顶板中间的应变大于四周应变，且在顶板边缘会出现负应变。

(3)顶板厚度为1d，2d时冲切体为圆台，顶板厚度为3d时顶板发生无征兆的破坏无冲切体产生。且随着顶板厚度的增加冲切体的母线逐渐向内部挤压，冲切体的顶面底面半径逐渐减小，直至无冲切体冲出。

(4)基于不同破坏模式给出了溶洞顶板最小安全厚度理论计算公式，理论值与试验值吻合较好。

(5)溶洞顶板发生弯拉破坏时，溶洞跨度对其影响较大，因此溶洞跨度对破坏模式及极限承载力的影响值得后续研究深入探讨。

[1] 赵明华,陈昌富,曹文贵,等.嵌岩桩桩端岩层抗冲切安全厚度研究[J]. 湘潭矿业学院学报,2004,18(4): 41-45. [ZHAO M H, CHEN C F, CAO W G,etal. Analysis for the safe terrane thickness of punching-shear resistance at the end of rock-socketed piles[J]. Journal of Xiangtan Mining Institute, 2004, 18(4): 41-45.(in Chinese)]

[2] 赵明华,曹文贵,何鹏祥, 等. 岩溶及采空区桥梁桩基桩端岩层安全厚度研究[J]. 岩土力学,2004,25(1):64-68. [ZHAO M H，CAO W G，HE P X，etal. Study on safe thickness of rock mass at end of bridge foundations pile in karst and worked-out mine area[J]. Rock and Soil Mechanics，2004，25(1)：64-68.(in Chinese))

[3] 雷勇,陈秋南,马缤辉.基于极限分析的桩端岩层冲切分析[J]. 岩石力学与工程学报, 2014, 33(3): 631-638. [LEI Y, CHEN Q N, MA B H. Punching analysis of rock at pile tip base on limit analysis[J]. Chinese Journal of Rock Mechanics and Engineering,2014,33(3)： 631-638.(in Chinese))

[4] 龚先兵,赵明华,杨明辉,等. 岩溶区桥梁基桩极限承载力的突变求解方法[J]. 公路交通科技, 2012, 29(11): 53-57. [GONG X B, ZHAO M H, YANG M H,etal. Determination of ultimate bearing capacity of pile in karst region based on catastrophe theory[J]. Journal of Highway and Transportation Research and Development, 2012, 29(11): 53-57. (in Chinese)]

[5] JIANG Chong, LIU Lang, WU Jun-ping. A new method determining safe thickness of karst cave roof under pile tip[J]. Journal of Central South University, 2014, 21(3): 1190-1196.

[6] 黎斌,范秋雁,秦凤荣.岩溶地区溶洞顶板稳定性分析[J]. 岩石力学与工程学报, 2002, 21(4): 532-536. [LI B, FAN Q Y, QIN F R. Analysis on roof stability of karst cave in karst areas[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(4): 532-536. (in Chinese)]

[7] 孙映霞,王金安,张智浩. 岩溶区桩基破坏模式研究及稳定性分析[J]. 工业建筑, 2012, 42(9): 96-102. [SUN Y X，WANG J A, ZHANG Z H. Failure pattern study and stability analysis of pile foundation in karst area[J]. Industrial Construction,2012,42(9): 96-102. (in Chinese))

[8] 尹凯丽,郝世龙. 武汉地区岩溶对桩基承载力影响数值模拟研究[J]. 水文地质工程地质,2015,42(6):96-102. [YIN K L, HAO S L. A study of the effect of karst on the bearing capacity of pile foundation in Wuhan district based on numerical simulation[J]. Hydrogeology amp; Engineering Geology,2015,42(6):96-102. (in Chinese)]

[9] MENETREY P. Synthesis of punching failure in rein-forced concrete[J]. Cement amp; Concrete Composites, 2002(24): 497-507.

[10] 刘铁雄.溶洞顶板与桩基作用机理分析与模拟试验研究[D].长沙:中南大学,2003:70-90. [LIU T X. Mechanism analysis and simulation test of karst cave roof and pile foundation[D].Changsha: Central South University, 2003:70-90. (in Chinese)]

[11] 刘铁雄,彭振斌.溶洞顶板模拟试验研究[J].探矿工程,2002(6):1-4. [LIU T X, PENG Z B. Simulation test study of karst cave roof[J]. Prospecting Engineering, 2002(6):1-4. (in Chinese)]

[12] 张慧乐,张智浩,王述红,等.岩溶区嵌岩桩的试验研究与分析[J].土木工程学报, 2013, 46(1): 92-103. [ZHANG H L, ZHANG Z H, WANG S H,etal. Experimental study and analysis of rock-socketed pile in karst area[J]. China Civil Engineering Journal, 2013, 46(1): 92-103. (in Chinese)]

[13] 张慧乐,马凛,张智浩,等.岩溶区嵌岩桩承载特性影响因素的试验研究与分析[J]. 岩土力学,2013，34(1)：92-101. [ZHANG H L，MA L，ZHANG Z H，etal. Test Research and analysis of influencing factors of rock-socketed pile bearing capacity in karst area[J]. Rock and Soil Mechanics，2013，34(1)：92-101.(in Chinese)]

[14] 徐挺.相似理论与模型试验[M]. 北京:中国农业机械出版社, 1982. [XU T. Similarity theory and model test[M]. Beijing: Chinese Agricultural Machine Press, 1982. (in Chinese)]

责任编辑

：张明霞

Laboratorymodeltestsonpunchingpropertiesofkarstcaveroofunderpiletipconsideringvariousthickness-spanratios

ZHAO Minghua, WU Gaoqiao, XIAO Yao, YANG Chaowei, XU Zhuojun

(GeotechnicalInstituteofHunanUniversity,Changsha,Hunan410082,China)

According to the similarity theory, punching properties of cave roof under pile tip are investigated through three series of large-scale laboratory model tests with different thickness. The load-displacement curves of pile foundation and roof, the ultimate strain curves of roof bottom and the failure characteristic of cave roof with different thickness are obtained. The test results show that the punching failure occurs within the circle table punching body when the thickness of the cave roof equals to 1d or 2d; however, the bending failure rather than the punching failure occurs when the thickness of the cave roof equals to 3d. The turning point of the elastic stage is transformed into the plastic stage in half the position of the ultimate bearing capacity according to the load-displacement curves, indicating that the plastic ultimate bearing capacity is two times the elastic ultimate bearing capacity. At last, the calculation formula of the minimum safety thickness is induced based on the theories of bending for thin plates and punching failure. The theoretical calculation results are in good agreement with the test results, which can meet the requirements of engineering calculation accuracy. The test results in this paper are based on critical situation, and they can provide reference for the preliminary design of piles in Karst areas.

roof failure mode; karst cave; model test; safety thickness

10.16030/j.cnki.issn.1000-3665.2017.06.05

TU 457；TU458+.4

A

1000-3665(2017)06-0029-08

2017-03-26;

2017-05-16

国家自然科学基金项目资助(51278187)

赵明华(1956-)，男，博士，教授，博士生导师，主要从事桩基础及软土地基处理研究。E-mail: mhzhaohd@21cn.com