基于GLRT零速检测算法的行人室内定位系统*

樊启高,孙 艳,孙璧文,庄祥鹏

(江南大学物联网工程学院,江苏 无锡 214122)

基于GLRT零速检测算法的行人室内定位系统*

樊启高*,孙 艳,孙璧文,庄祥鹏

(江南大学物联网工程学院,江苏 无锡 214122)

针对微机电系统中惯性传感器漂移大、精度低导致室内行人定位精度不高的问题,本系统在惯性导航解算算法的基础上,提出基于广义似然比检验的零速检测算法。该方法是利用广义似然比检验对行人处于站立相或摆动相的概率进行估计以及进行零速更新,提高行人定位精度。基于本文提出的行人室内定位模型,搭建以惯性测量单元为核心的实验平台,评估本文算法的可行性。实验结果表明行人定位的动态误差为-1.814 1 m～1.451 6 m,置信度为97.61%。表明本文的行人室内定位系统满足实际定位的要求。

行人室内定位;惯性导航解算算法;广义似然比检验;零速检测算法;惯性测量单元;

现在的定位与导航技术已经比较成熟,在人们日常的生活中,各种设备中的系统都在为人们提供地理信息服务,如手机导航[1],车载导航系统[2],等,这些定位与导航技术基本是基于全球定位系统GPS(Global Position System)[3]。由于现在城市化进程的加快,大而密封的室内环境日益增多,各种高楼和地下场所也层出不穷。因此基于无线传感器网络[4]、RFID[5]、ZigBee[6]、蓝牙[7]等室内定位技术也日渐兴起。同时这些技术易受室内环境的干扰,因此可克服室内复杂环境的基于微机电惯性测量单元 MEMS IMU(Micro-Electro-Mechanical System-Inertial Measurement Unit)[8]的行人室内定位技术被提出。MEMS IMU不易受外界环境因素的干扰并具有自主性,可满足在封闭的无射频信号的室内环境下定位技术的要求。

目前行人室内定位算法是分为两种,一种是行人航迹推算PDR(Pedestrian Dead Reckoning)算法[9],其主要包括航向估计、布频估计、步长估计以及滤波。PDR算法虽降低对传感器精度的要求,但精度不能满足复杂的室内环境的要求;另一种为基于零速更新ZUPT(Zero Velocity Update)[10]的惯性导航系统INS(Inertial Navgation System)算法[11],其具有精度高,稳定好等特性,可满足室内行人定位要求。

目前,一些学者利用加速度计、陀螺仪输出值,得到其峰值、幅值或方差,与设定的阈值进行比较,提取出行人步态中的零速区间,进行零速更新[12-13]。但易受惯性元器件输出累积误差的影响,存在零速点不能完全被提取以及零速点误判等问题。因此本文提出的基于广义似然比检验法GLRT(Generalized Likelihood Rate Test)[14]的零速更新算法是对行人处在站立相和摆动相的概率进行估计,结合GLRT对速度实时检测并修正,提高捷联惯性导航系统的解算精度。

为验证本文算法的合理性和精确性,分别做3组不同速度下的加速度峰值检测+角速度阈值法,加速度峰值检测+角速度阈值+时间阈值法以及基于GLRT的行人步态零速区间检测法提取零速点的精确度的实验,以及室内行人定位轨迹对比实验。实验结果表明本文的行人定位系统满足实际要求。

1 室内行人定位算法

本文提出的行人定位算法包括惯性导航解算算法、步态区间检测算法以及滤波算法。如图1所示,通过加速度计以及陀螺仪的输出值进行惯性导航系统解算得到速度、姿态以及位置,同时步态区间检测算法判断行人处于何种步态,进行零速更新,结合扩展卡尔曼滤波EKF(Extended Kalman Filter)对速度、姿态、位置进行修正,提高行人定位系统的精度。

图1 室内行人定位算法结构图

1.1 惯性导航解算算法

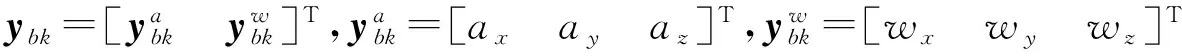
图2 MEMS IMU的三轴方向示意图

IMU的输出误差是随着时间的增加而增加,因此对加速度和角速率减去由EKF估计出的误差值,得到补偿后的角速率值、加速度值:

(1)

(2)

从载体坐标系转换到导航坐标系,需要通过姿态矩阵的过渡,因此:

(3)

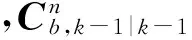
(4)

随后更新在k时刻未经EKF修正的速度、位置值:

(5)

(6)

rn,k|k-1=rn,k-1|k-1+vn,k|k-1×Δt

(7)

经过EKF修正后的速度、位置值为:

(8)

(9)

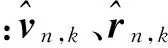
随后更新在k时刻的姿态矩阵:

(10)

式中:∂θk表示小角度的反对称矩阵:

(11)

式中:∂φk表示在k时刻转动的小角度。

1.2 步态区间检测算法

行人的行走的步态可以分为两种情况:摆动相和站立相;摆动相表示此刻行人的脚在运动阶段,站立相表示此刻的行人的脚与地面完全接触阶段。理论上行人处于站立相的时刻,角速度值和水平加速度值应为零以及竖直方向的加速度值应等于重力常量。多数的静态区间检测算法是基于对IMU输出参量的模值、方差以及幅值和已设定的阈值进行比较,提取出步态中的零速点。这类算法一方面易受到IMU的误差积累的影响;另一方面行人在行走过程中,足部与地面的接触时间特别短,这类算法易误判零速区间导致丢失零速点,导致行人的速度、位置误差增加。本文提出的静态区间检测算法是通过对行人处于站立相、摆动相进行概率分配,再根据GLRT算法,确定出行人的站立相。

设行人处于摆动相的状态值为:H0,处于站立相的状态值为:H1。假设H1为真值时,此时行人处于摆动状态的概率表达式为:PFA=Pr{H1|H0},以及假设H0为真值时,行人处于摆动状态的概率表达式为PD=Pr{H1|H1}。根据Neyman-Pearson定理,最大化PD,使PFA=a(a表示显著水平,根据实际情况给定)[15]。若:

(12)

表示此刻行人是处于H1。式中:γ表示检测的阈值,L(#)表示对于每一个Zn的值的似然比(即对于H0、H1假设的可能性)。

阈值γ的确定取决于:

(13)

若假设行人处于H0状态,对比力和角速度进行建模、分析是有难度的。因此通常是假设行人处在H1状态,则以下两种情况是成立:①加速度计测量的比力值,只是由于地面对万有引力的对峙加速度,其大小是已知的。②IMU的姿态是不变的,即它的角速度为零。

即:

(14)

(15)

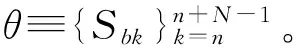
在系统中,θ是不可以忽略的,本文采用了极大似然估计法对θ进行估计,并结合式(12)得到:

(16)

(17)

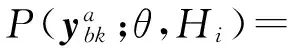
(18)

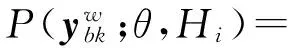
(19)

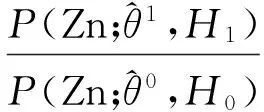
(20)

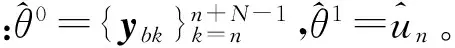
可得:

(21)

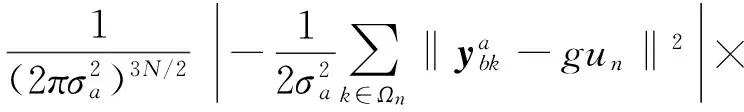
(22)

式中:un∈Ωu。

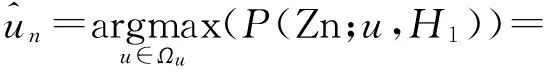
(23)

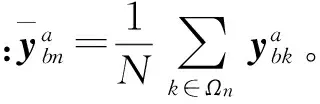
(24)

所以,式(20)变为:

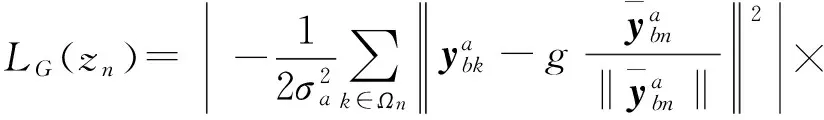
(25)

简化式(25),基于GLRT的行人零速区间检测算法公式如下:

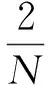
(26)

(27)

式中:γ′=-2ln(γ)/N。γ′根据实际情况而定。

2 扩展卡尔曼滤波

扩展卡尔曼滤波可以运用非线性化的系统[16],因此在惯性导航系统中有着广泛的应用。

在本文中,EKF的状态估计值为:

(28)

状态一步预测方程:

(29)

状态矩阵:

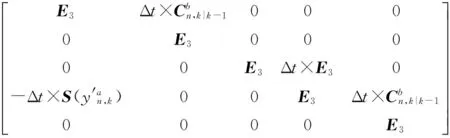
(30)

(31)

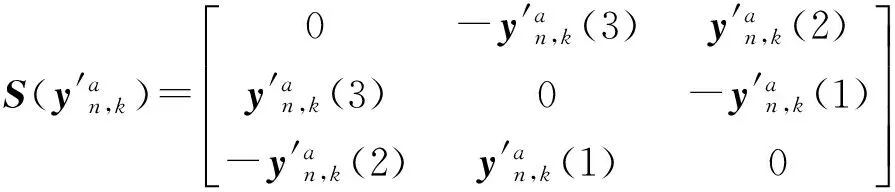
(32)

量测方程:

(33)

式中:Zk表示在k时刻的量测值,H表示量测矩阵,nk表示的量测噪声矩阵。

3 实验验证与结果分析

3.1 实验配置

实验采用荷兰Xsens公司的Mti系列MEMS IMU。它主要由3个相互正交的加速度计、3个陀螺仪及1个三轴磁传感器组成,MEMS IMU中的传感器性能表如表1所示。

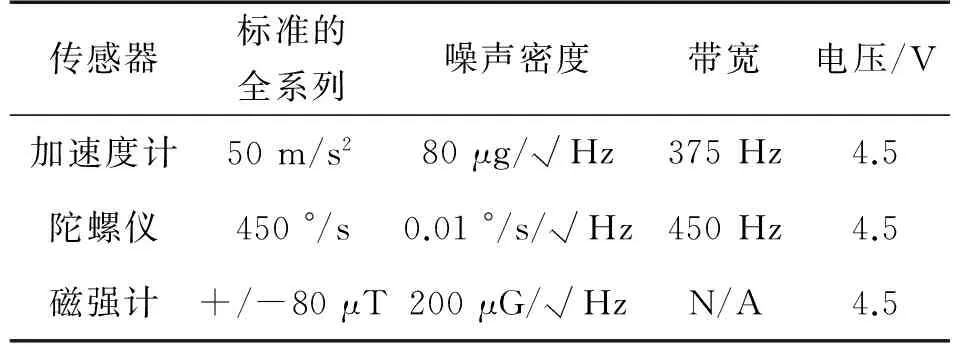
表1 MEMS IMU的性能参数

3.2 实验结果与分析

为验证本文的行人航迹推算算法的正确性,进行3组对比实验进行验证。

3.2.1 静态检测对比实验

实验过程中,将MEMS IMU安装在右脚上进行以下几组实验。

通过MEMS IMU数据的收集,利用加速度峰值检测加角速度阈值的静态检测算法、加速度峰值检测加角速度阈值加时间阈值的静态检测算法以及基于GLRT的零速更新算法分别计算行人在不同速度下的行走的步数。

实验结果如表2所示,通过数据对比说明基于GLRT的零速更新算法更能快速有效的检测出行人行走的步数,其正确性以及精确性得到验证。

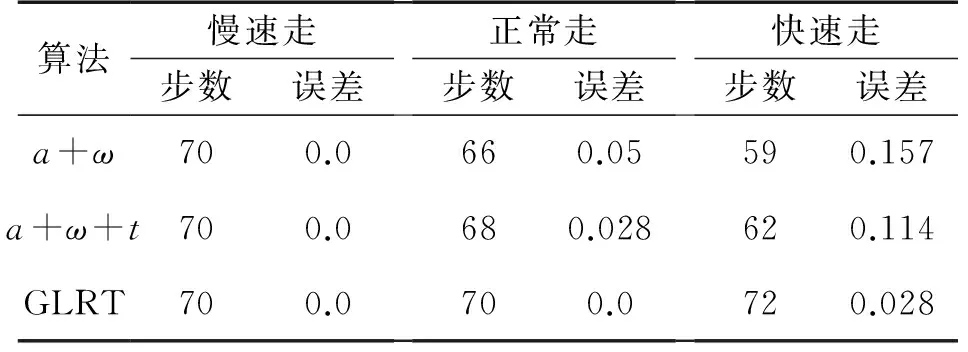
表2 不同方法对不同运动模式的步数检测

3.2.2 零速更新算法验证实验

为了验证基于GLRT的零速更新算法的有效性,进行基于GLRT的零速更新算法的值与加速度、角速度的幅值的对比实验。

在图3和图4中,通过对基于GLRT的零速更新算法的值与加速度、角速度的幅值进行对比,表明基于GLRT的零速更新算法可准确且快速地检测行人的站立相,因此证明该算法可实时进行零速修正。图6表示基于GLRT的零速更新算法对速度进行修正,结果表明速度可得到及时有效的更新,行人定位的精确性得到提高。

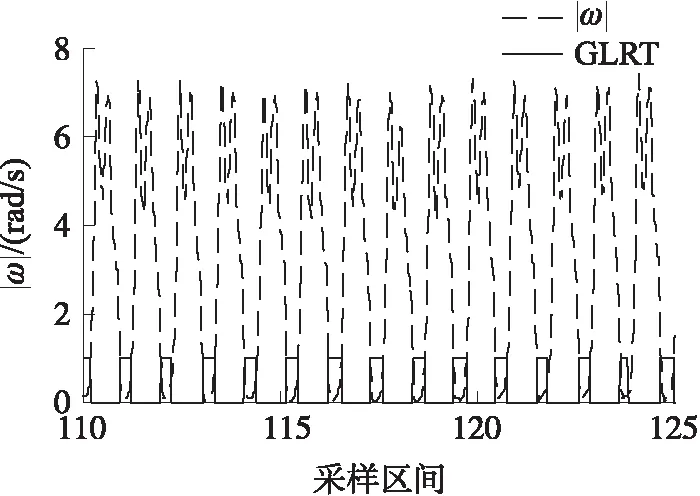
图3 |ω|与GLRT的对比

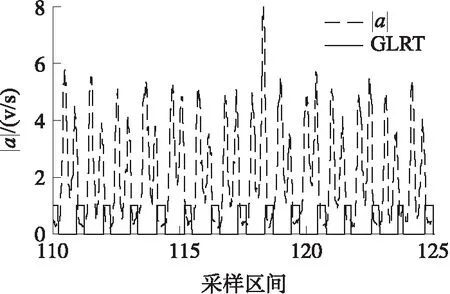
图4 |a|与GLRT的对比

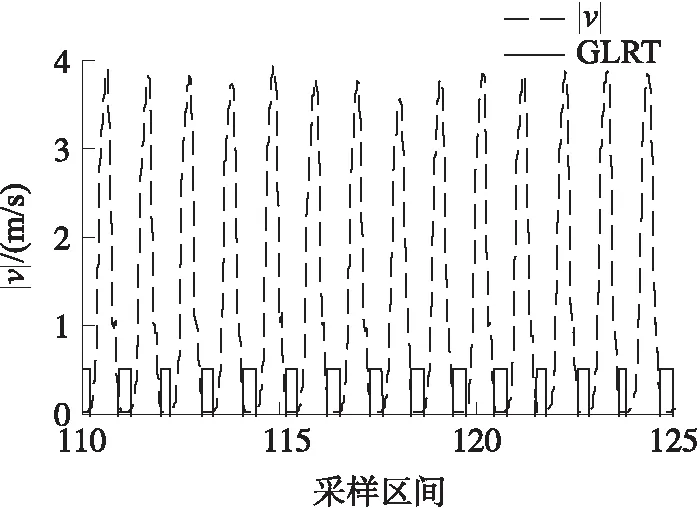
图5 GLRT对|v|的修正

3.2.3 行人定位轨迹对比实验

为了验证本文中的行人定位算法的有效性,在室内的空地处进行行人轨迹对比实验。

图6表示的是各个行人轨迹图,实验结果如表3所示,实验数据表明:提出的基于GLRT零速检测算法的行人定位算法的定位效果稳定且不存在发散问题,同时定位效果优于另两种算法。

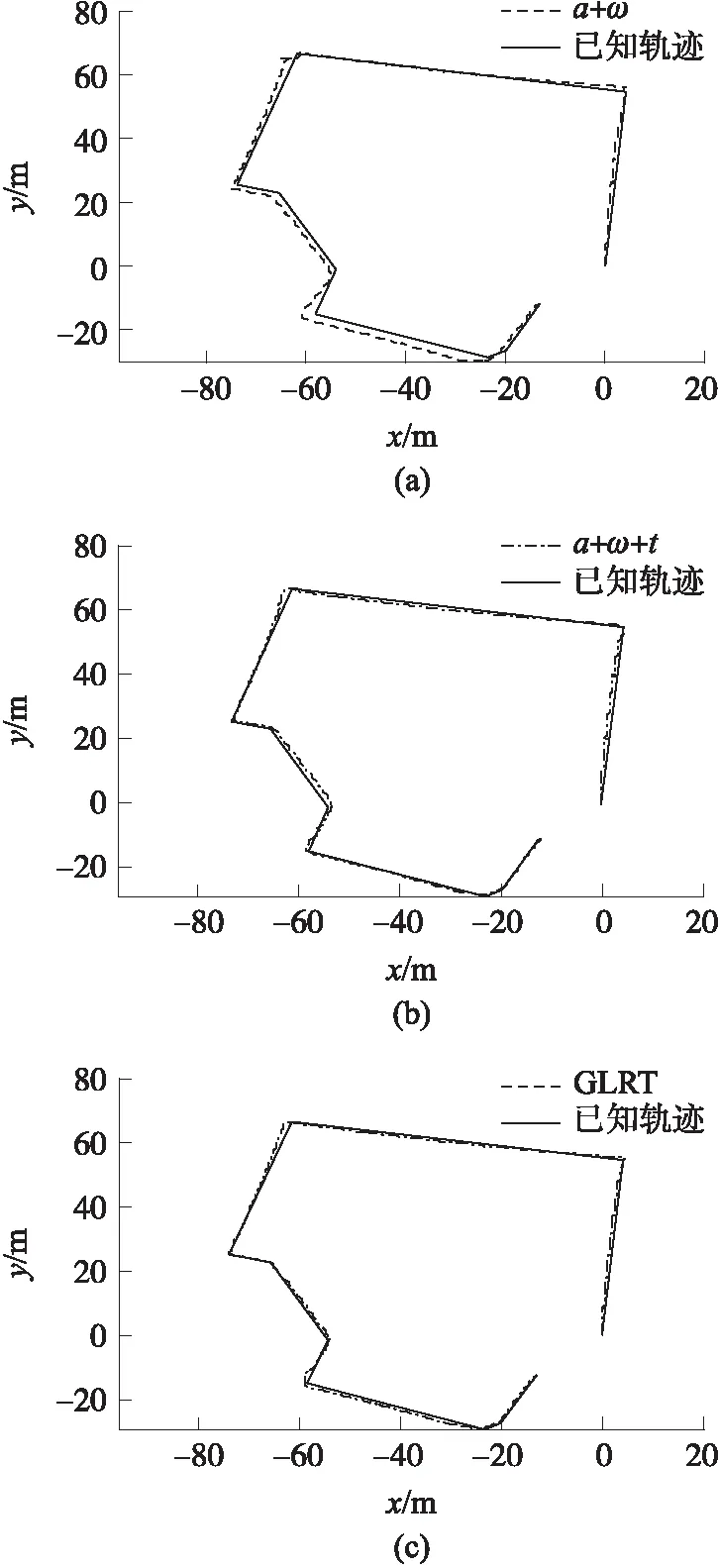
图6 行人定位轨迹图

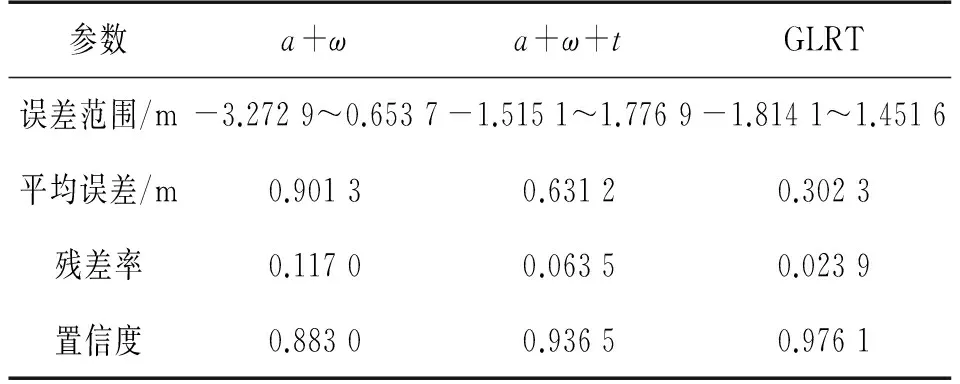
参数a+ωa+ω+tGLRT误差范围/m-3.2729～0.6537-1.5151～1.7769-1.8141～1.4516平均误差/m0.90130.63120.3023残差率0.11700.06350.0239置信度0.88300.93650.9761

4 结束语

本文的基于GLRT的行人步态零速区间检测算法对行人的站立相进行实时的检测,使行人的零速更新的效果更稳定、更精确。因此,基于该零速检测算法的行人定位算法相比较于其他行人定位算法,定位效果最佳。实验结果表明提出的定位算法置信度为0.976 1,定位效果稳定,满足实际生活中定位的要求。

[1] 唐荣年,曾雄梅. 基于北斗卫星和蓝牙技术的Android手机导航系统设计[J]. 武汉理工大学学报,2015,37(6):104-108.

[2] Large D R,Burnett G,Benford S,et al. Crowdsourcing Good Landmarks for in-Vehicle Navigation Systems[J]. Behaviour and Information Technology,2016:1-10.

[3] 吴甜甜,张云,刘永明,等. 北斗/GPS组合定位方法[J]. 遥感学报,2014,18(5):1087-1097.

[4] 朱素文,曾宪华,胡梦. 改进的局部保持典型相关分析的无线传感器网络节点定位方法简[J]. 传感技术学报,2016,29(10):1579-1588.

[5] Ruiz A R J,Granja F S,Honorato J C P,et al. Accurate Pedestrian Indoor Navigation by Tightly Coupling Foot-Mounted IMU and RFID Measurements[J]. IEEE Transactions on Instrumentation and Measurement,2012,61(1):178-189.

[6] Cheon J,Hwang H,Kim D,et al. IEEE 802.15. 4 ZigBee-Based Time-of-Arrival Estimation for Wireless Sensor Networks[J]. Sensors,2016,16(2):203.

[8] 李超,苏中,朱嘉林. 可穿戴式自主定位技术的零速触发算法研究[J]. 传感技术学报,2014,27(5):627-632.

[9] 王亚娜,蔡成林,李思民,等. 基于行人航迹推算的室内定位算法研究[J]. 电子技术应用,2017,43(4):86-89.

[10] Lan K C,Shih W Y. On Calibrating the Sensor Errors of a PDR-Based Indoor Localization System[J]. Sensors,2013,13(4):4781-4810.

[11] 冯培德. 论混合式惯性导航系统[J]. 中国惯性技术学报,2016(3):281-284.

[12] 王普,潘凯,任明荣,等. 基于伪自适应阈值零速检测法的室内个人导航系统[J]. 北京工业大学学报,2015,41(9):1308-1313.

[13] 李超,苏中,朱嘉林. 可穿戴式自主定位技术的零速触发算法研究[J]. 传感技术学报,2014,27(5):627-632.

[14] Sang S,Zhai R,Zhang W,et al. A Self-Developed Indoor Three-Dimensional Pedestrian Localization Platform Based on MEMS Sensors[J]. Sensor Review,2015,35(2):157-167.

[15] Sengijpta S K. Fundamentals of Statistical Signal Processing:Estimation Theory[J]. Technometrics,1995,37(4):465-466.

[16] 安雷,张国良,张维平,等. 移动机器人扩展卡尔曼滤波定位与传感器误差建模[J]. 信息与控制,2012,41(4):406-412.

樊启高(1986-),男,汉族,江西南昌人,江南大学物联网工程学院副教授,主要研究方向为智能传感与控制;

孙艳(1993-),女,汉族,江苏盐城人,无锡江南大学物联网学院在读研究生,主要研究方向为封闭环境内导航定位;

庄祥鹏(1993-),男,汉族,福建泉州人,江南大学物联网工程学院研究生,主要研究方向为智能传感与控制。

PedestrianIndoorPositioningSystemBasedonGLRTZeroSpeedDetection*

FANQigao*,SUNYan,SUNBiwen,ZHUANGXiangpeng

(Jiang Nan University,School of IOT Engineering,Wuxi Jiangsu 214122,China)

Due to the inertial sensors’s large drift and low accuracy in micro electro mechanical system,the accuracy of pedestrian indoor location is low. Based on the inertial navigation,this paper presents the zero speed detection algorithm of the generalized likelihood ratio test. This algorithm uses the generalized likelihood ratio test to estimate the probability of pedestrians standing or swinging,and updates the speed of the standing,in order to improve the accuracy pedestrian location. Based on the proposed indoor pedestrian location model,build an experimental platform with the inertial measurement unit,and evaluate the feasibility of the model. The experimental results show that the dynamic error is -1.814 1 m～1.451 6 m,and the confidence level is 97.61%,and indicate this pedestrian indoor positioning system meets the requirements of practical location.

pedestrian indoor location;inertial navigation;generalized likelihood ratio test;nertial measurement unit

TP212

A

1004-1699(2017)11-1706-06

项目来源:国家自然科学基金项目(51405198);中央高校专项自主科研项目(JUSRP11464);江苏省2016年度普通高校研究生实践创新计划项目(SJZZ16_0219)

2017-03-23修改日期2017-07-07

10.3969/j.issn.1004-1699.2017.11.016