压裂中的流体摩擦阻力及效应分析

孟琪 关元 郝健坤

(西安石油大学， 陕西 西安 71000)

压裂中的流体摩擦阻力及效应分析

孟琪 关元 郝健坤

(西安石油大学， 陕西 西安 71000)

在压裂过程中，由于管柱中流体压力、温度、摩阻等的影响，使得管柱受力与变形较为复杂。本文首先将压裂液作为非牛顿流体处理并假设为典型的幂律流体；其次对压裂过程中流体摩阻对管柱所产生的摩阻力、轴向变形、压降等进行分析；最后，通过算例的验证发现：将压裂液作为非牛顿流体处理比以往基于牛顿流体的分析更合理。

压裂;非牛顿流体;摩阻;轴向变形

0 引言

在计算压裂中的流体摩阻时，一般将压裂液作为牛顿流体来处理，但这样所带来的误差与实际情况相去甚远。本文将压裂液作为非牛顿流体处理，采用非牛顿流体中最典型的幂律流体，在此基础之上分析流体摩阻所产生的各种效应。

1 压裂过程中的摩阻分析

在流体摩阻的分析过程中，做出以下假设：

①管径恒定不变，不考虑管柱组配的装置引起的能量损失；

②压裂液为非牛顿流体，且认为其为幂律流体。

1.1 压裂过程中的流体摩阻力计算

单位重量流体的沿程损失用 表示，称为沿程水头损失。由流体力学达西公式得：

则作用在单位长度的管柱上的流体摩擦阻力为：

其中流体在管中的流动速度可用压裂当日压裂总流量来近似计算为：

式中： λ为流体摩阻系数；l为管柱长度，m；d为管柱内径，m；v为流体在管柱内的平均流速，m/s；g为重力加速度，m/s2；ρ 为流体密度，kg/m3；Q 为当日压裂总量，m3。

1.2 流体摩阻引起的管柱轴向变形

由于流体摩阻力所引起的管柱轴向应力为σf，由材料力学知识可得：

由于流体摩阻力所引起的管柱轴向变形记为ΔLf，由材料力学公式有：

则ΔLf的计算公式为：

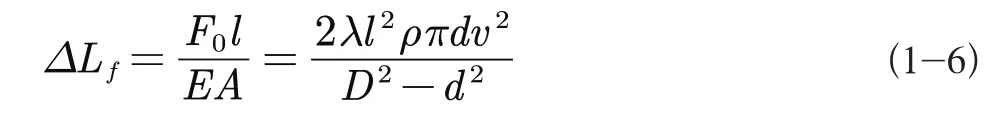
式中：σf为流体摩阻力所引起的管柱轴向应力，MPa； A为管柱的横截面积，m2； D为管柱的外径，m； ΔLf为流体摩阻力所引起的管柱轴向变形，m； E为管柱材料的弹性模量，MPa。

1.3 压裂过程中的压降分析

由流体力学知识可知：将圆管两端的压降记为ΔP，则：

其中，λ的确定可以按照在2．1中幂律流体流态以及摩阻系数确定方法来确定。

2 算例分析

已知某井在压裂过程中所使用的压裂液为非牛顿流体，其流性指数为0．8293，稠度指数为0．4248 Pa·S，密度为1．89g/m3，井深为3200 m，压裂排量为2．5 L/min ，管柱外径88．9mm，管柱内径76mm。则，按照上述公式和数据，使用Mathematica软件进行计算，得如下结果(各个量的单位均与公式中所述一致)：

①计算管柱横截面液体流速：将Q=2．5 L/min，d=76×10-3m，代入公式(1-3)得V=2．29621m/s。

② 计 算 压 裂 液 的 雷 诺 数：将V=2．29621m/s，d=76×10-3m，ρ=1890g/mm3，n=0．8293，k=0．4248 Pa·S，代入幂律流体雷诺数计算公式得Re=1900．45。幂律流体在该流动环境下的层流临界雷诺数为：Re=2333．86，判断流动状态为层流。

③计算压裂液的摩阻系数：将Re=1900．45代入幂律流体摩阻系数计算公式得f=0．00841。

④计算压裂液的沿程水力损失：将f=0．00841，l=3200m，d=76×10-3m，g=9．8m/s2代入公式(1-1)得hf=95．36。

⑤计算压裂时所受到的流体摩阻力：将hf=95．36，ρ=1890g/mm3，d=76×10-3m，g=9．8m/s2代 入 公 式(1-2)得F0=32050．2N。

⑥计算压裂管柱的横截面积为：0．0005318mm3。

⑦计算流体摩阻所产生的应力：将F0=32050．2N代入公式(1-4)得σf=6．026×107N/m2。

⑧计算流体摩阻而造成的管柱轴向变形量：将F0=32050．2N，l=3200m，E0=2×1011Pa代 入 公 式(1-6)得ΔL=0．964m。

⑨计算流体摩阻而造成的压降：将f=0．00841，ρ=1890g/mm3，d=76×10-3m，V=2．29621m/s代 入 公 式(1-7)得ΔP=7．065×106Pa。

3 结论

本文主要对压裂过程中流体对于管柱的摩阻进行了分析。首先，假设压裂液为非牛顿流体，并对使用最为广泛的幂律流体进行了介绍；其次，通过流体力学知识、材料力学知识对流体摩阻进行了分析；最后，通过算例分析以验证上述公式的合理性。本文得出了：

(1)压裂液作为非牛顿流体，采用幂律流体进行处理，给出其摩阻系数、雷诺数的计算公式；

(2)通过流体力学知识，分析得到了压裂过程中流体的沿程水力损失、流体摩阻力、流体摩阻力所产生的轴向变形、流体沿管柱的压降公式等。

[1]李子丰，戴江，于振东.两层压裂井下管柱力学分析及其应用[J].石油钻采工艺.2009，30(1)：81-84.

[2]王毓震，杨文斌，姚顺利，等．浅层水平井管柱摩阻与力学分析[J].钻采工艺，2012，35(4)：80-87.

[3]窦益华，吕维平，张福祥，等.支撑式跨隔测试管柱力学分析及其应用[J].石油钻采工艺，2007，29(4)：106-109.