基于强化学习算法的自适应配对交易模型

胡文伟，胡建强，李 湛，周剑峰

1 上海工程技术大学 管理学院，上海 201620 2 复旦大学 管理学院，上海 200433 3 上海社会科学院 应用经济研究所，上海 200020 4 国泰君安证券公司 固定收益部，上海 200120

管理科学

基于强化学习算法的自适应配对交易模型

胡文伟1，胡建强2，李 湛3，周剑峰4

1 上海工程技术大学 管理学院，上海 201620 2 复旦大学 管理学院，上海 200433 3 上海社会科学院 应用经济研究所，上海 200020 4 国泰君安证券公司 固定收益部，上海 200120

配对交易是统计套利中最主要的交易策略，但随着市场有效性的逐渐提高，该策略的获利机会正变得越来越有限，传统的固定参数交易模型已难以保证配对交易一直获得最大利润，交易模型的参数不仅需要优化，而且还需要动态地、自动地调整优化值，因此有必要研究开发具有人工智能属性的参数动态优化交易模型，这对于提升交易模型的盈利能力和执行效率具有重要意义。

自适应配对交易模型是对传统的协整配对交易策略进行改进，推出一种基于强化学习模式的新型统计套利交易模型；将Sarsa强化学习算法和ε-greedy策略与新模型相结合，把模型参数的确定方法由传统的主观经验法和固定参数法改进为自适应模式的动态参数优化法；编制的计算机程序仿真实现了基于新模型的套利交易全过程，涵盖模型参数的动态优化、套利交易的模拟操作以及交易绩效的测量评估；以中国债市交易量最大的5种债券为样本，构建4组配对组合，采用Johansen协整检验法、T检验和Robust稳健性检验等方法对交易模型和测试结果进行实证分析。

研究结果表明，新模型的运行效果全面优于传统模型。新模型显著提升了交易系统的获利能力，收益率和索提诺比率大幅提高；同时降低了投资风险，最大回撤出现明显下降；还提高了套利交易的执行效率，交易次数明显减少，套利成本下降；具有持续学习的能力，能促进累计收益率不断上升并最后收敛于最大值。研究结果还表明，协整配对交易在中国债券市场同样具有有效性，能够获得显著正收益。

将强化学习思想与协整配对交易策略相结合，设计开发出一种新型配对交易模型，实现了模型参数的自适应动态调整。这种改进型交易模型有助于应对传统配对交易策略获利能力的下降，进一步提高配对交易策略的效率和绩效。在中国融资融券和股指期货等做空机制开闸的市场环境下，新模型可为投资者提供一种有效的套利手段和风控工具。

协整配对交易；Sarsa强化学习算法；自适应；动态参数；优化；仿真；统计套利

引言

配对交易是量化投资和统计套利中最主要的交易策略，目前量化投资已成为成熟市场最主流的投资方式之一，更被视作资本市场成熟与否的一个重要标志。在中国，随着做空机制逐渐放松，尤其是融资融券和股指期货的推出，以协整配对交易为代表的主流量化交易方式也开始出现兴起之势。

大量实证研究证实了协整配对交易策略的有效性，不论是海外还是中国市场，在资产配对组合选择得当的前提下，协整配对交易策略可成功抓住统计套利机会并获取收益。而且，由于套利收益本质上来源于市场的非有效性，因此配对交易在欠成熟市场有着更广阔的前景。

然而，随着配对交易从神秘走向普及以及市场非有效性的逐渐改善，该策略的获利机会正变得越来越有限。在现有的交易模型中，评估时间窗口、交易时间窗口、开仓阈值、平仓阈值等主要参数往往采用经验值或固定常数。已有研究表明，传统的主观经验法和固定参数法虽然方法简单，但却具有局限性，不能保证配对交易一直获得最大利润。另外，传统策略的使用前提(如残差的方差不变性等理想条件)实际上往往难以满足，金融资产价格的时间序列通常存在明显的异方差性，这意味着协整配对交易的最优交易区间和最优止损区间等参数设置不能固定不变，否则，区间过窄会导致交易频率过高并增加交易成本，区间过宽则会造成反应迟钝而错失获利或止损时机。

这些现状导致准确选择交易模型参数被推到越来越重要的位置。已有研究认为，交易模型的参数不仅需要优化，而且更需要动态地调整优化值。为此有学者引入GARCH模型，计算动态的价差标准差，以此作为交易信号；有学者提出基于O-U过程的套利策略；还有学者提出对经验性的选择参数进行遍历性研究，循环查找最优阈值。这些改进方案都在各自特定的数据样本上取得了一定成效，但同时也受到新的适用条件的很大约束，要么需要符合GARCH模型或O-U过程，要么需要预设经验性参数等专家系统，而且不能应对环境发生的超预计变化。

基于上述分析，本研究认为有必要开发无需知识背景、无需预定义的自适应模式的参数动态优化策略。本研究把在人工智能领域得到成功应用的强化学习思想引入配对交易策略，帮助交易模型的参数实现自适应动态优化。这种改进型配对交易系统不必受制于预设模型的约束，不必依赖专家系统的存在和限制，不必担忧环境发生超预计变化，它在分析和处理的过程中能够根据环境变化实时地、高效地、自动地、智能地、自适应地进行参数优化，从而使交易模型的参数始终保持优化状态。

这种改进型交易模型有助于提升协整配对交易的盈利能力和执行效率，在中国融资融券和股指期货等政策开启的环境下，为投资者提供一种新型、有效的低风险投资策略模型。

1 相关研究评述

1.1协整配对交易

配对交易是统计套利和量化投资中最重要、最主流的投资策略[1]，这种新颖的交易策略最早出现于20世纪80年代的美国，一经推出便获得空前成功。GATEV et al.[2]、GRANGER[3]、JOHANSEN[4]最早提出配对交易的思想和基本原理之后，众多学者对协整配对交易展开了多角度和多市场的研究，主要围绕协整配对交易的两个核心问题展开，一是配对组合选择，二是交易模型设计。这两个环节紧密相关，但在研究进程上，前者起步早且研究相对充分，后者起步晚并有难题待解。

第1个环节主要涉及配对组合选择、协整关系检验和配对交易有效性论证，目前已经取得大量成果。VIDYAMURTHY[5]和HUCK[6-7]为配对组合的选择和检验提供了理论和方法，其他众多学者的上百篇文献实证检测了配对交易策略在全球各大宗商品市场、股市个股和股指期货市场的有效性，大量研究结果表明配对交易策略在全球大部分市场皆有效。但是，随着套利交易普及化和市场有效性逐步提高，统计套利的获利机会变得越来越有限。BOTOS et al.[8]研究配对交易策略在东西欧市场的回报情况，结果表明，1993年至2013年西欧和东欧市场的配对交易回报率分别为16.98%和20.74%，投资组合的Sharpe比率分别仅为0.57(西欧)和0.92(东欧)，与之前10年的1.89(西欧)和1.39(东欧)相比明显下降。在中国，由于受到卖空机制的制约，此方面的实践和研究滞后于海外成熟市场数十年，但目前已在迎头赶上，尤其在配对组合选择和配对交易有效性两个方面。相关研究已经很多，在最新的研究中，胡伦超等[9]、赵胜民等[10]和高辉等[11]分别以内地主要指数成份股、融资融券标的股、股指期货交易数据等为对象，实证分析交易的有效性；LIU et al.[12]还研究了中国双重上市股票的套利机会。众多研究结果皆表明，配对交易策略同样适用于中国市场，而且配对交易在中国更多地表现为一种短期策略。

配对交易第2个环节主要涉及交易模型设计和最优参数确定。这部分研究起步较晚，但空间极大，而且随着套利获利机会趋弱，亟须进一步的深入研究。该环节的重点是确定模型参数，包括开仓时间、平仓时间、持仓时间、交易期限、投资仓位等阈值。在早期时，确定参数大多采用主观经验法。之后学者们开始推出各种技术手段对参数进行优选，其中，进场和离场规则的最优参数求解吸引了最多研究者。KUO et al.[13]研究了采用背离策略的配对交易的最优平仓点，并用数值分析案例对其结论给出例证。所谓背离策略是指在配对股票价格走势出现背离时开仓，当价差触及目标线或止损线时进行平仓，该策略的隐含假设是配对股票的价差服从均值回归过程。SONG et al.[14]用HJB方程来刻画价值函数，其研究结果表明，最优平仓问题可以通过一系列quasi-algebraic方程得以解决，给出了数值分析案例；LARSSON et al.[15]研究价差服从Levy过程的含跳跃模型的平仓优化问题，求证了可优化性的必要条件，采用有限元方法对误差给出精确估计模型，并对最优解的存在性和唯一性给出例证。另有学者对交易模型参数进行综合研究。NGO et al.[16]把交易规则简化为3种组合结构之间的最优切换问题，即A和B皆空仓、A长仓B短仓、A短仓B长仓，证明最优切换点的存在，并用数值仿真方法给出例证；ZENG et al.[17]综合研究统计套利中的资产组合选择、参数边界寻优和最优交易策略设计等一系列问题。截至目前，配对交易领域的大部分研究都是基于投资组合理论和统计分析方法，但也有少数学者开始将随机控制[18]、遗传算法[19]、神经网络[20]、粒子群算法[21]、人工蜂群算法[22]等其他领域的研究方法运用进来。此外，学者们也针对中国市场进行类似研究。欧阳红兵等[23]针对中国A+H股的价格数据进行实证分析，采用数值算法研究交易持续期、交易间隔期和交易次数等最优阈值；唐国强等[24]针对中国白糖期货合约数据，利用切比雪夫不等式和夏普比率在回归残差的基础上构建套利阈值统计量，在利润最大化的前提下求得最优阈值；麦永冠等[25]构建折回首日WM-FFBD策略，结合GGR和Herlemont策略，运用3种检验方法，研究在沪深港证券市场交易中建仓策略对配对交易年收益率的影响。

随着参数寻优研究的深入，学者们开始注意到不合适的模型参数对配对交易收益率的不利影响以及固定参数和静态模型的局限性。DO et al.[26]在重新检验最早的GGR模型[2]的收益能力时发现，配对交易的收益率呈下降趋势，背后原因并非交易者增多导致的交易机会减少，而是GGR模型设定的交易期太短，导致很多配对因交易期结束而被强行平仓；HUCK[6]用S&P100成分股进行配对交易，测试了不同的形成期长度和开仓阈值，也发现配对交易的收益率受形成期长度的影响；邵超等[27]对A股历史数据进行实证检验后也发现，配对交易的收益率与形成期和交易期的长度有关。这些研究结果皆说明，交易期和形成期等期限的长短对交易收益率有显著的影响，而固定不变的预定期限无法因应市场情况的变化作出调整，因而注定难以获取最大收益。一些学者的研究为这种变化找到了理论依据，ALEXAKIS[28]在研究了若干股指的长期协整关系后发现，这种长期关系会受到市场表现的影响，当市场趋势显著改变时，投资者应该重新构建套利组合；张河生等[29]从异方差的角度进行分析，对股指期货进行模拟配对交易测试，结果表明经验型模型参数不能保证交易一直获得最大利润，必须考虑异方差的存在，固定的模型参数会丧失很多交易机会，甚至导致巨大的亏损，应该通过不断调试来选择参数最优值。

针对传统模型存在的缺陷，学者们提出一些改进策略和模型。一种思路是考虑异方差和ARCH效应，建立基于GARCH模型的协整套利策略，代表性研究包括李世伟[30]、彭舒怡[31]和何树红等[32]，这些学者的实证检验皆证实其改进型模型比传统策略获得了更好的套利效果。另外一种思路是尝试将固定参数改为动态参数，刘阳等[33]将神经网络与动态GARCH模型相结合，通过挖掘价格偏差中的非线性特征，使动态GARCH模型能够更及时地发现波动性的变动，从而降低传统静态模型的预测偏差；邢恩泉等[34]对协整配对交易策略进行改进，利用计算机快速循环运算的特点，对经验性选择参数进行遍历性研究，循环查找最优配对组合和建仓阈值，从而具有根据数据变化自我动态修正的功能。

上述改进方案都在各自的特定数据样本上取得一定成效，但是这些方案转而又受到新的使用条件约束，要么需要符合GARCH模型或O-U过程等，要么需要预设经验性参数等专家系统，而且不能应对环境发生超预计变化，因而这些方案仍然具有一定的局限性。因此，有必要开发一种无需知识背景、无需预定义并且能够跟随环境变化做出自适应调整的动态优化策略，这应该是进一步提高配对交易效率和绩效的重要突破口。

1.2强化学习

强化学习(reinforcement learning,RL)是机器学习的一种主要模式，强化学习的相关算法在没有知识背景和预定义的情况下通过数值化处理能够表现出强大的学习能力，能够在与环境的交互中学习行为策略。强化学习模式在人工智能和计算机控制领域已经得到较多的实际应用并取得佳绩。Google的Deep Mind公司一直是这方面的领先者，SILVER et al.[35]关于强化学习算法结合人工神经网络应用于游戏开发以及进行人机围棋挑战的研究，其研究成果AlphaGO机器人挑战前围棋世界冠军，并获得举世瞩目的胜利。

强化学习模式在金融领域也得到一些应用。SU-TTON et al.[36]认为，在金融相关问题的求解上，不确定性和动态性是必要的组成部分，因此强化学习算法很适合这类问题的求解。目前强化学习模式在金融领域主要运用于证券交易尤其高频交易和投资组合管理。LEE et al.[37]提出一个基于强化学习算法的股票交易框架，利用多智能体的Q-learning算法，通过定义必要的角色，做出投资决策并进行股票仿真交易，他对韩国股市的测试表明该方法比其他类似方法具有更好的性能。TAN et al.[38]使用自适应网络模糊推理系统的人工智能模型，基于强化学习算法，提出一个非套利型的高频交易系统。不过，强化学习模式虽然已开始在金融领域有所应用，但相对于其他领域，在金融领域的应用还只是处于起步阶段，在配对交易和统计套利上的具体应用和技术开发更是处于空白。

在众多强化学习算法中，Q-learning学习和Sarsa学习是两个重要的算法，前者是一种离策略，后者是一种在策略，后者的效果通常好于前者，不过标准Sarsa算法对状态空间有要求，必须是离散的且空间数较小。在中国，Sarsa算法已开始应用在不少新兴产业，应用最多的是机器人控制[39]，其次是交通信号控制[40]、网络建模[41]和组织运作过程控制[42]等。但是，在金融领域的应用尚有待开发。

2 相关理论和模型

2.1强化学习的基本原理

强化学习又称增强学习、加强学习、再励学习或激励学习，与监督学习、统计模式识别和人工神经网络等构成机器学习的主要模式，是人工智能领域的关键技术。但有别于传统的机器学习，强化学习的一大优点是无需预设专家系统，无需预知被控对象和环境的模型，具有鲜明的自适应能力，具有实时学习和终身学习的能力。

强化学习的目标是在与环境的试探性交互中学习行为策略，以求获取最大长期奖赏。对强化学习过程的描述见图1，强化学习系统涉及两个主体，即作为行动者的智能体和智能体所处的环境，环境拥有各种可能的复杂状态，所有状态构成状态集S。在t时刻，当智能体面对环境状态st(st∈S)及前一时刻(t-1)环境状态改变的瞬时奖赏值rt时，可在其行为集A中选取一个合适的行为或称动作at(at∈A)来执行，于是环境状态转移到st+1，同时智能体立即得到来自环境状态改变的瞬时奖赏值rt+1，根据此奖励，智能体更新其在st状态和at动作上获得的经验，然后决策下一时刻(t+1)的at+1动作。依此循环往复，智能体通过与环境不断地交互作用，不断尝试并调整自身行为，不断学习如何把状态映射到动作以获得最大长期奖赏。

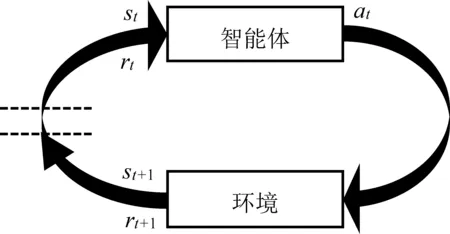
图1 强化学习过程Figure 1 Process of Reinforcement Learning

在上述过程中，强化学习系统还需具备其他几个核心要素，即策略函数、状态转移概率函数、奖赏函数和值函数。

(1)策略函数即决策函数D:S→A，用以确定所有状态下智能体需要进行的动作。Dt(s,a)为在t时刻、s状态下选择a动作的概率，或者说把s状态映射至a动作的概率，此种映射即为策略。

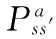
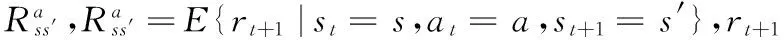
(4)值函数有两种形式，即状态值函数VD(s)和状态行为值函数QD(s,a)。状态值函数用来估计s状态对于智能体来说究竟好到什么程度，其衡量指标采用未来总的期望奖赏。由于未来奖赏还有赖于未来的动作，因此该函数还与具体的策略D有关。VD(s)为从s状态开始一直采用D策略得到的期望奖赏，即

(1)

其中，ED为一直采用D策略所对应的期望值；γ为未来奖赏值折现至现时的折扣率，γ∈[0,1]；rt+k+1为从(t+k)时刻至(t+k+1)时刻的瞬时奖赏值，k=0,1,2,…,∞。

QD(s,a)为状态行为值函数，也称状态-动作对值函数，其函数值称为Q值，表示在s状态下实施a动作并且以后一直采用D策略时的期望奖赏，即

(2)

上述两种值函数是估计未来全部奖赏值折现后的总值，皆是对长期效果的全局性评价，两者都可用作目标函数。强化学习系统的任务就是求得最优策略D*，使值函数达到最大，即

D*=argDmaxVD(s),s∀S

(3)

2.2Q-learning算法和Sarsa算法

强化学习的主流算法目前包括动态规划算法、蒙特卡洛算法和瞬时差分算法，瞬时差分算法因收敛效果好而被广泛采用。比较流行的瞬时差分算法包括Q-learning算法和Sarsa算法，两者均以状态行为值函数Q(s,a)为目标函数，是对马尔科夫决策过程框架下的强化学习问题的求解。Q-learning算法的状态行为值更新过程为

Qt+k+1(st,at)=Qt+k(st,at)+ΔQt+k

(4)

其中，Qt+k(st,at)为(t+k)时刻的Q值，其起始值Qt(st,at)为随机值，也可设置为0；α为学习率，α∈[0,1]，在学习过程中从1到0不断衰减。在一定条件下，Q-learning采用贪心法即可保证收敛。

Sarsa算法是一种基于策略的算法，可视作改进的Q-learning算法，其迭代公式为

Qt+k+1(st,at)=Qt+k(st,at)+ΔQt+k

ΔQt+k=α[rt+γQt+k(st+1,at+1)-Qt+k(st,at)]

(5)

可以明显看出，Q-learning算法是采用最大值进行迭代，是一种离策略，与模型无关。而Sarsa算法则是采用实际Q值进行迭代，是一种在策略，它与模型有关。虽然在策略一般好于离策略，但是标准Sarsa算法对状态空间有一定要求，空间必须是离散的，而且空间数较小。

从迭代公式还可看出，α越大则当前学习对Q值的影响越大。学习过程刚开始时，智能体没有任何经验，α接近于1，用实际累积回报作为Q的估计值；随着时间推移，智能体不断学习，知识的积累越来越多，对状态的评估越来越重要，α就应该下降；最后，α趋近于0，智能体只是通过对状态的评估来选择最好的行动。

2.3协整配对交易基本原理

配对交易是统计套利和量化投资中最重要、最主流的交易策略，在各种投资组合策略中，配对交易具有自融资和市场中性的特点，其收益与大市的相关度很低，牛熊市和横盘市皆可获利。目前主流的配对交易策略包括协整配对交易法(简称协整套利法或协整法)、随机价差法和最小距离法，建立在协整理论基础上的协整法应用最为广泛。协整理论为一些原本不能使用经典回归分析法的非平稳序列开辟了一种建模途径，有些非平稳序列经过线性组合后却可能成为平稳序列，此类构造出来的平稳的“协整组合”或称协整方程可以用来解释变量之间长期稳定的均衡关系，而且资产组合短期的暂时偏离可被视为统计套利的机会。

协整法的核心是，认为协整组合的资产价格具有均值回复性，即价差围绕均值水平上下波动，并会以很高概率向均值回归。当组合资产的价差偏离历史均值时，预期这种背离在未来会得到纠正，因而认为出现了套利机会，从而做空价格较高资产并买入价格较低资产，等价差回归长期均衡水平时再反向平仓操作，由此赚取价差收敛带来的收益。

由此可见，协整配对交易主要涉及两大工作，一是选择配对资产，二是设计交易模型。首先，从市场上找出相关性较高的资产进行配对，并检验其间是否存在协整关系，常用方法有两种，即Engle-Granger两步协整检验法和Johansen协整检验法。两种方法都是首先将两个时间序列做回归，然后针对残差项做平稳性检验，若是平稳的，就认为存在协整关系。两种方法的主要差别在于，前者采用一元线性回归方程，后者采用多元方程技术，因此Johansen检验法在假设和应用上的限制较少。

协整配对交易的第2个重要环节是设计交易模型，其核心工作是设计和确定模型参数。最重要的参数有4个，即评估时间窗口、交易时间窗口、开仓阈值和平仓阈值。评估时间窗口主要用于协整测试，以评估协整参数和系数，重新评估价差方程；交易时间窗口是止损触发器，如果时间序列超过了交易时间窗口仍然没有收敛到均值，那么就会进行强行止损；开仓阈值是开仓指示器，当配对资产的价差超越开仓阈值时，将产生交易信号和开仓动作；平仓阈值是另一个止损触发器，平仓阈值宽于开仓阈值，当配对资产的价差不断远离长期的价格中枢，并超越平仓阈值时，就将强行平仓止损，这是配对交易最重要的风控措施。4个参数的优化原则是投资组合的综合绩效最大化，目前常用的绩效评定指标包括夏普指标、特雷诺指标、詹森指标、特雷诺-布莱克估价比率和索提诺比率等。

3 模型设计和仿真测试

3.1基于强化学习模式的协整配对交易模型

如前所述，在传统的协整配对交易模型中，模型参数往往采用静态常数，但由于金融资产价格的时间序列存在明显的异方差性，因此该方法具有相当大的局限性。针对此传统模型的缺陷，一些参数调整型改进方案已取得一定成效，但是又受到新的使用条件的约束，而且不能应对环境发生的超预计变化，因此仍然具有不可忽视的局限性。为此，本研究将强化学习的思想和算法引入交易模型设计，不仅帮助模型实现参数调整，而且助其实现自适应模式的动态优化。

基于强化学习模式的改进型配对交易系统见图2，在该系统中交易决策系统承担交易指令的决策和执行，是整个配对交易系统的核心，对应于强化学习系统中的智能体；证券市场和证券价格是配对交易系统中的环境及环境状态；投资绩效评估指标被用作奖赏值；评估时间窗口、交易时间窗口、开仓阈值、平仓阈值4个参数构成智能体的行为，并以实时动态调整的方式进行工作。

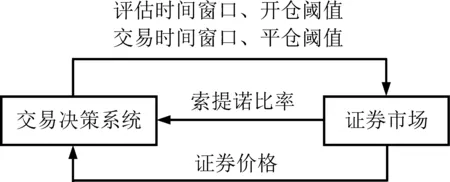
图2 基于强化学习模式的配对交易决策过程Figure 2 Workflow of RL Pairs Trading System

整个系统的工作流程从预设4个参数初始值开始，智能体密切监控环境状态，当配对资产的价差偏离长期价差中枢并触及开仓阈值时,智能体将指示对配对资产组合进行相应的开仓操作；在持仓建立后,智能体继续不断地监控和评估环境状态，并实时动态地调整参数值；一旦配对资产的价差缩小并回到价差中枢以下，或者价差继续扩大并触及平仓阈值，二者中发生任意一个便会触发平仓止损操作，同时输出奖赏值作为奖励；然后，当前的信息和值函数被更新,算法重新进行迭代，智能体继续密切关注环境状态，等待下一次投资组合建仓；如此循环往复，直至投资期终结。在整个决策运行过程中，智能体不断地根据每次投资组合的开仓和平仓获得的经验以及环境状态的变化动态调整最优参数。

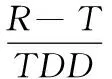
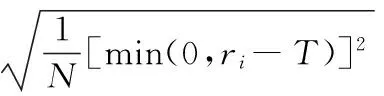
(6)

其中，ri为第i期的收益率，N为总期数。(6)式表明，当交易策略定为最大化收益且同时防范回撤风险时，索提诺比率是一个很好的交易策略性能评定指标。

在目前使用最广的两个强化学习算法(即Q-learning算法和Sarsa算法)中，Q-learning是一种与模型无关的离策略算法，Sarsa算法则与模型有关，是一种在策略。虽然Sarsa算法对状态空间在数量和离散性上有一定的要求，但配对交易涉及的状态空间能够比较容易地符合这些要求。考虑到在策略的效果一般好于离策略，而且本研究主要是验证模型的有效性，因此采用Sarsa算法进行研究。

在配对交易模型涉及的4个参数中，开仓阈值和平仓阈值属于连续型参数，本研究通过均分处理为其做离散化，每0.1个单位抽取一个数值，这样处理后，所有参数皆为离散型，所有参数的每一种排列组合被视为一个动作。Sarsa算法的迭代公式为

Qk(st,at)=Qk-1(st,at)+α[rt+γQk-1(st+1,at+1)-

Qk-1(st,at)]

(7)

此外，为了避免陷入局部最优，本研究采用ε-greedy探索策略，在选取动作时引入一定程度的随机变化来解决开发与利用之间的平衡问题，即以概率1-ε(ε∈[0,1])利用已有策略，以概率ε搜索新的策略。在学习初期，ε可选较大值，随着时间推移，智能体的学习在加深，经验在丰富，随机性便可逐渐降低，ε逐渐减小。

在本研究编制的算法中，首先对动作进行初始化，为评估时间窗口、交易时间窗口、开仓阈值和平仓阈值4个参数设定初始值；然后，选择足够数量的迭代来训练智能体；最后，依据ε-greedy策略优化上述4个参数的具体值来作为智能体的动作。根据前面提出的方法，索提诺比率作为计算奖励的指标，其返回值(即奖赏值)在学习过程中通过环境不断反馈给智能体，最后，索提诺比率在完成所有任务后还要作为最终数据输出。交易模型所对应的计算机流程图见图3。

3.2仿真测试的数据和样本

为了更好地结合中国市场的实际情况，本研究以产品品种多、流动性好、可借券卖空的中国债券市场为研究对象。在具体品种上，本研究选择交易量最大的3年期国债、5年期国债、7年期国债、3年期金融债和3年期AAA信用债，按照期限相同或发行主体相同的原则，将上述债券组成3年期国债-5年期国债、5年期国债-7年期国债、3年期国债-3年期金融债、3年期国债-3年期AAA信用债4组配对组合。

由于债券的日收盘价存在局部不连续现象，因而本研究选择中债收益率估值曲线作为具体研究数据，该数据源的截面数据不仅连续，而且与真实成交价最为贴近。本研究以每日估值收益率作为离散时间序列进行实验测试，原始数据来自于WIND数据库，选取2004年至2016年全部数据，数据的统计信息见表1。鉴于债券在某些特定日期会出现单日大幅跳跃但次日复原的特殊情况，该现象虽然对交易模型影响巨大，但在实际操作中可以人为地主动预判并加以控制，因此对实盘交易的影响并不大，因而本研究将这类数据作为异常点进行过滤处理。

3.3协整关系检验

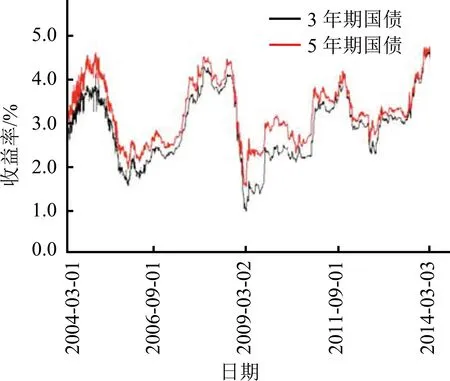
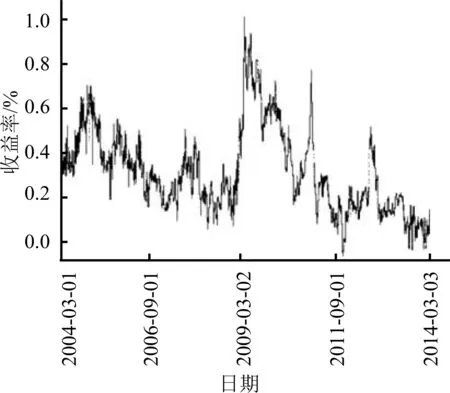
从直观看，以3年期国债-5年期国债这组配对组合为例，两个债券的收益率随时间推移向同一方向移动，见图4(a)。图4(b)为其收益率差值图，更直观地反映出两者之间的协整关系，价差围绕均衡位置上下波动。其他3组配对组合也存在类似现象。

本研究采用Johansen协整检验法进行协整检验。以3年期国债-5年期国债配对组合为例，检验结果显示，似然比检验值为31.90，0.10、0.05、0.01水平的临界值分别为17.85、19.96、24.60。31.90均大于这些临界值，表示在90%、95%、99%置信水平上拒绝了不存在协整关系的假设，即3年期国债与5年期国债的价格之间存在协整关系。其他3组配对组合也都得到类似的检验结果，在90%置信水平上全都存在显著的协整关系。

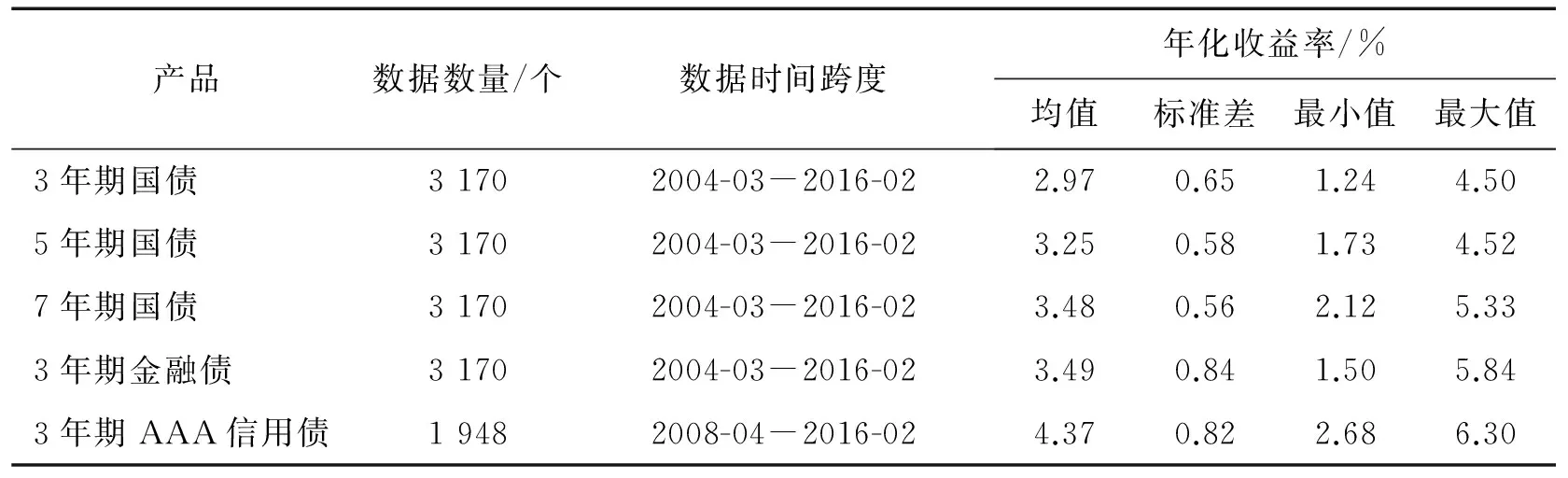
表1 样本数据的统计信息Table 1 Statistics of the Sample

注：3年期AAA信用债上市较晚，因而数据相对较少。

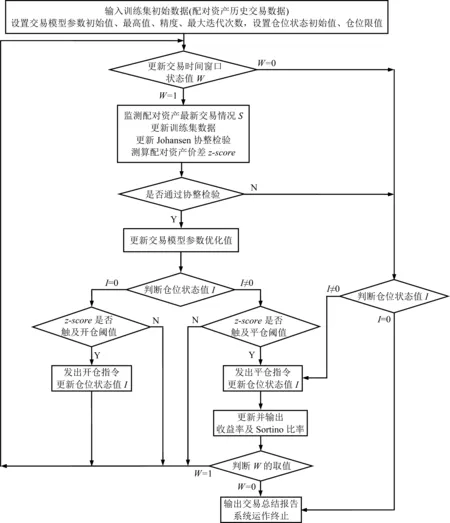
图3 基于强化学习模式的配对交易模型计算机流程图Figure 3 Computer Flow Chart of the RL Pairs Trading Model

3.4仿真配对交易结果和分析

在强化学习算法的操作中，需要提供训练集用于配对交易模型的学习，为此本研究选择样本中的75%数据作为样本训练集，其他数据作为测试集，见表2。整个训练过程迭代1 000次，在训练阶段α=1，ε=1。 4个参数的集合(即动作)通过ε-greedy策略进行选择，同时依据状态更新对应的值函数。在之后的测试阶段，智能体选择最优参数进行仿真交易。

以3年期国债-5年期国债这组配对组合为例，分别采用传统的静态参数协整配对交易模型(cointegration pairs model,CPM)和本研究提出的强化学习型动态参数协整配对交易模型(reinforcement learning model,RLM)进行仿真交易，测试在训练集和测试集中的效果。对于训练集，本研究通过传统的梯度寻优方法，为其选取表现最好的一组数值作为最优参数；对于测试集，本研究只是设定4个参数的选取范围和精度，由系统依据当前状态以及本研究设计的模型自动地、动态地选择出最优参数。

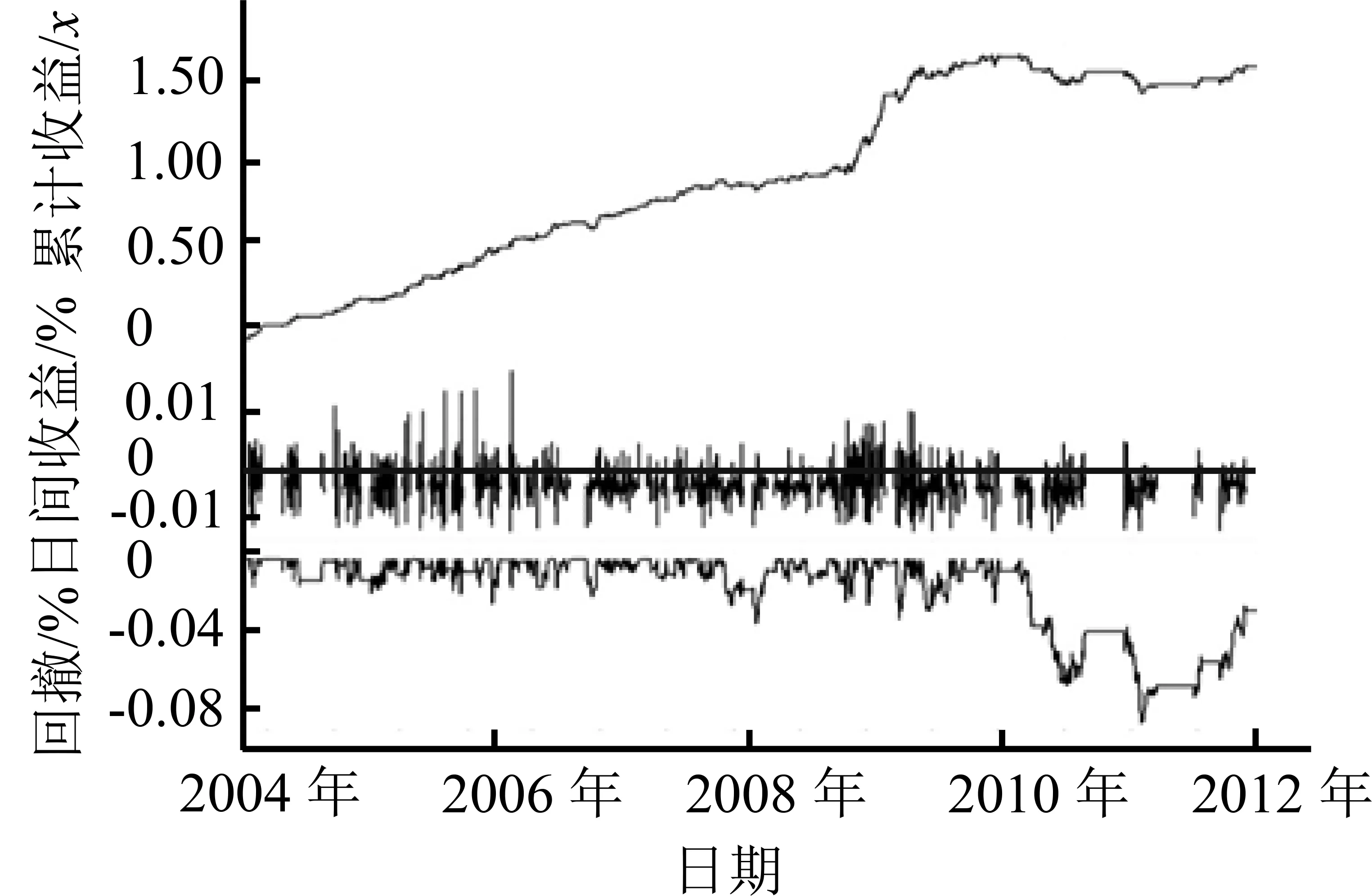
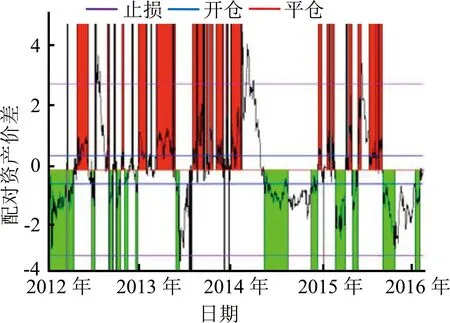
为了全面展示和比较两种交易模型的运行效果，本研究分别给出两种交易法在训练集和测试集的交易信号图和收益表现图。图5(a)和图5(b)给出传统配对交易法在训练集中的效果，图6(a)和图6(b)给出强化学习型配对交易法在训练集中的表现，图7(a)和图7(b)、图8(a)和图8(b)分别为两种方法在测试集中的表现。在交易信号图中，蓝色为开仓信号线，红色为平仓信号线，紫色为止损线，红色区块(上半部阴影区)表示持有组合多头，绿色区块(下半部阴影区)表示空头。在收益表现图中，可以看到累计收益率、日均收益率和最大回撤的动态情况。

(a)收益率 (b)收益率差值

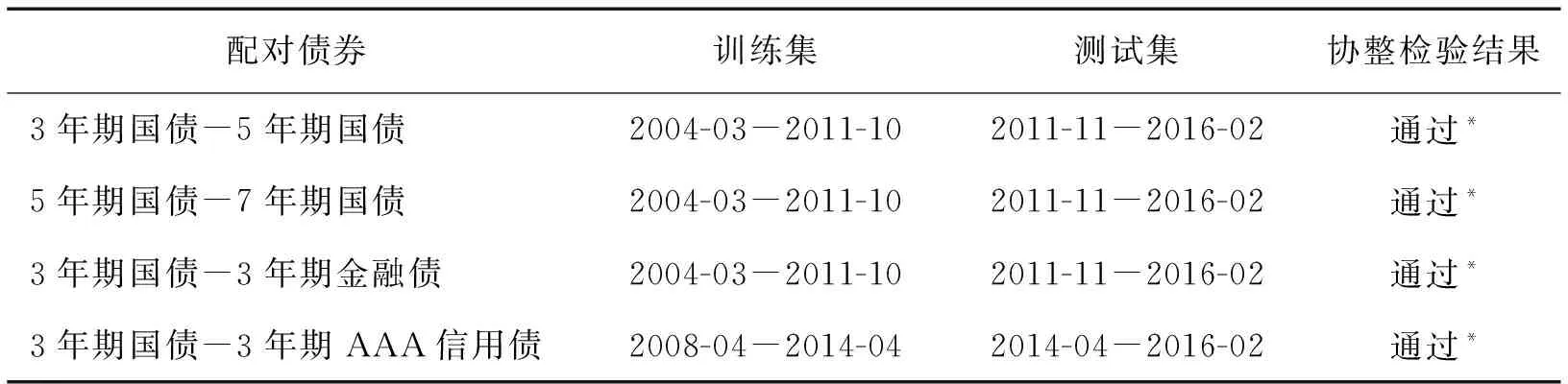
图4 3年期国债和5年期国债的收益率Figure 4 Historical Yields of 3Y Treasury and 5Y Treasury

注：*为在0.10水平上显著。

表3的上半部分第2列～第5列数据汇总了CPM和RLM在训练集和测试集中各项性能表现。在训练集上，RLM在收益和风险上的表现已经全面超越CPM。在测试集上，RLM的性能提高程度则更大，年化复合收益率从1.80%大幅提高至4.30%，索提诺比率也从0.04大幅提升至0.09；与此同时，承受的市场风险和操作风险不仅没有同步上升，反而明显下降，反映市场风险的最大回撤从6.50%降至5.70%，影响操作风险的交易次数从45次降至37次。

由于强化学习算法具有学习功能，因此在训练过程中，随着迭代次数的增多，会不断获得经验，最终可使累计收益率收敛于最大值。本研究的测试中，经过8 000次迭代后，系统的累计收益率达到最大值，见图9。

3.5稳健性检验

把新模型推广运用到本研究的全部4个配对组合，比较CPM与RLM两种方法的实施效果，仿真结果见表3。由表3可知，在测试集上，RLM的收益率比CPM算法大幅提高76%～383%；索提诺比率提高50%～125%；最大回撤也获得不同程度的下降，降幅最高达到62%。显然，RLM改进模型的运行效果全面地、显著地优于传统CPM模型。

为了对测试结果进行更严格的检验和分析，本研究进一步对两种方法在测试集上的收益率差异性进行显著性检验。各做15组测试，然后采用t检验对收益率均值之差进行假设检验，CPM和RLM的收益率及其差异的显著性检验结果见表4。检验结果表明，在95%甚至99%的置信水平上，基于强化学习算法的配对交易模型在收益率上显著优于传统的协整配对交易模型。

4 结论

4.1研究结果

本研究设计一种基于强化学习模式的配对交易模型，主要模型参数能够自动地进行动态优化，同时为该新模型设计并构建一个计算机交易系统，并进行仿真交易。仿真交易的测试结果表明，新模型的运行效果全面超越传统模型。新模型能够显著提升交易系统的获利能力，收益率和索提诺比率获得大幅提高；还能降低投资风险，最大回撤出现明显下降；提高了套利交易的执行效率，交易次数明显减少，套利成本得以下降；具有持续学习的能力，能促进累计收益率不断上升并最后收敛于最大值。测试结果还表明，协整配对交易在中国债券市场同样具有有效性，能够获得显著正收益。

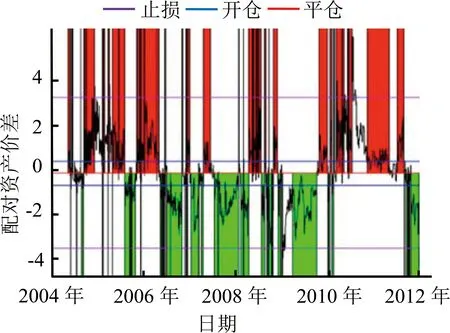
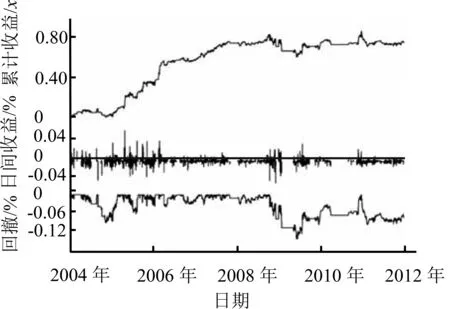
(a)交易信号图 (b)收益表现图

图5CPM在3年期国债-5年期国债配对组合上的仿真交易(训练集)
Figure5CPMSimulatedTradingon3YTreasury-5YTreasuryPair(inSample)

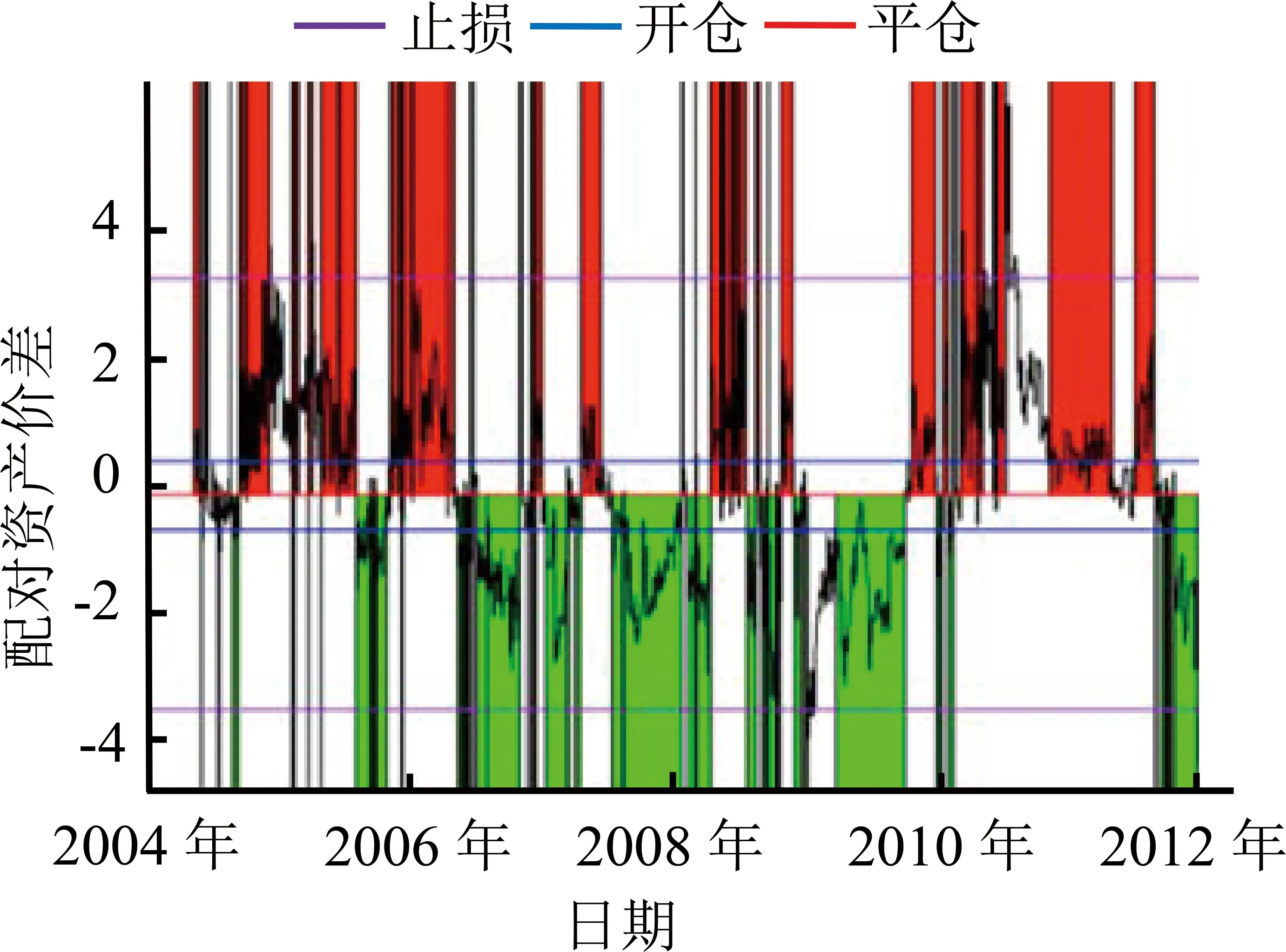
(a)交易信号图 (b)收益表现图

图6RLM在3年期国债-5年期国债配对组合上的仿真交易(训练集)
Figure6RLMSimulatedTradingon3YTreasury-5YTreasuryPair(inSample)

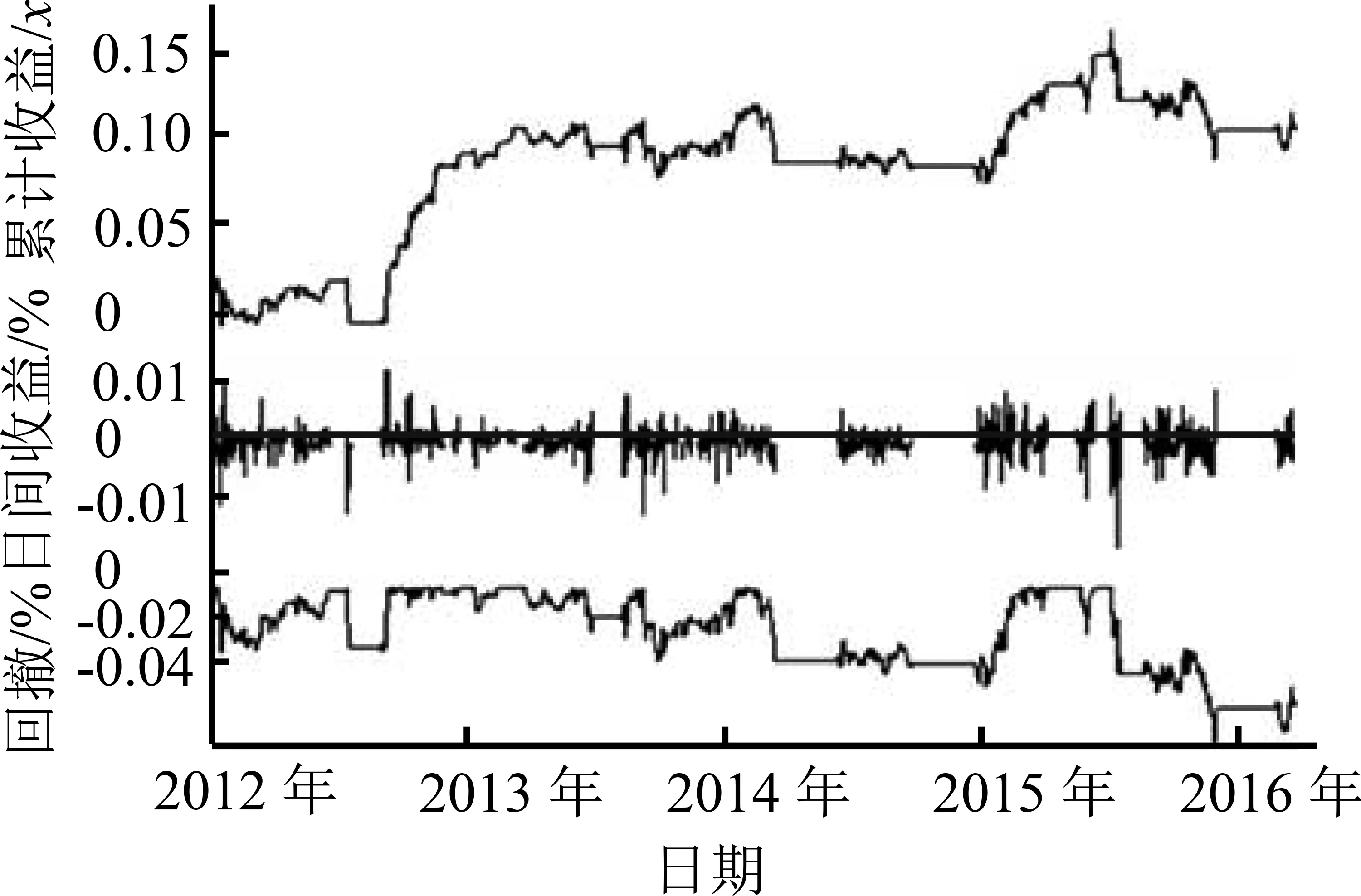
(a)交易信号图 (b)收益表现图

图7CPM在3年期国债-5年期国债配对组合上的仿真交易(测试集)
Figure7CPMSimulatedTradingon3YTreasury-5YTreasuryPair(outSample)

4.2技术贡献和应用价值

①本研究设计的新模型具有较大的应用价值，新模型为证券自动交易领域增添了一个新的交易策略和模型，有助于应对传统配对交易模型获利能力的下降，提升配对交易日渐式微的获利机会。②对传统交易模型进行了一次较大程度的改进，将强化学习思想与配对交易策略相结合，设计开发出一种新型配对交易模型，实现了模型参数的自适应动态调整。③随着中国融资融券和股指期货等做空机制和相关产品的不断开闸，新模型可为投资者提供一种新兴有效的套利手段和风控工具。④选择中国债券市场中交易量最大的5种债券为研究对象，填补了配对交易研究在国内债券市场上的空白。

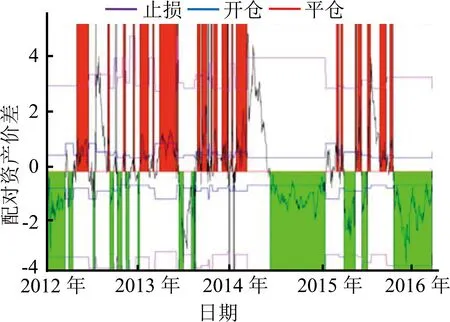
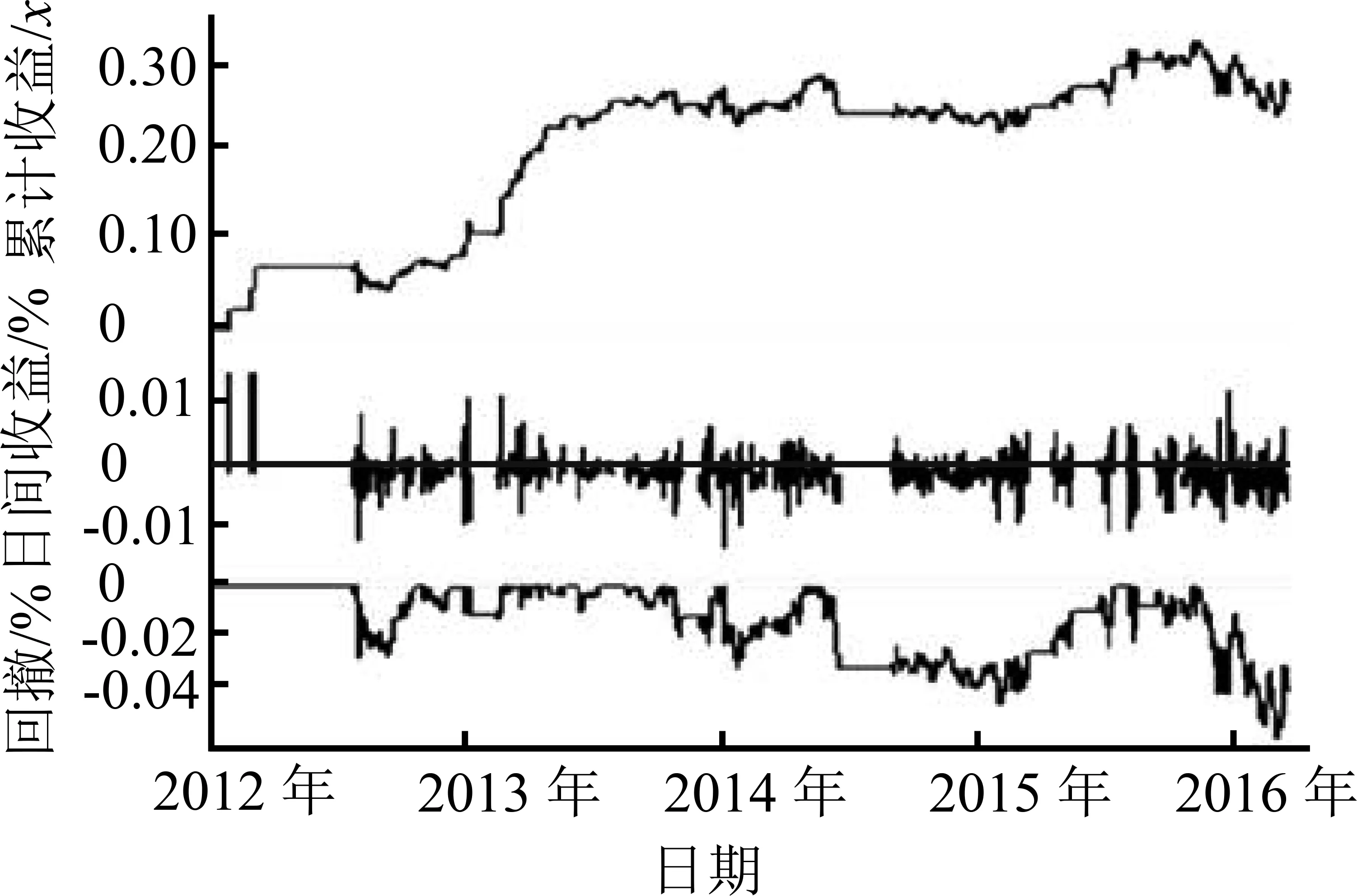
(a)交易信号图 (b)收益表现图

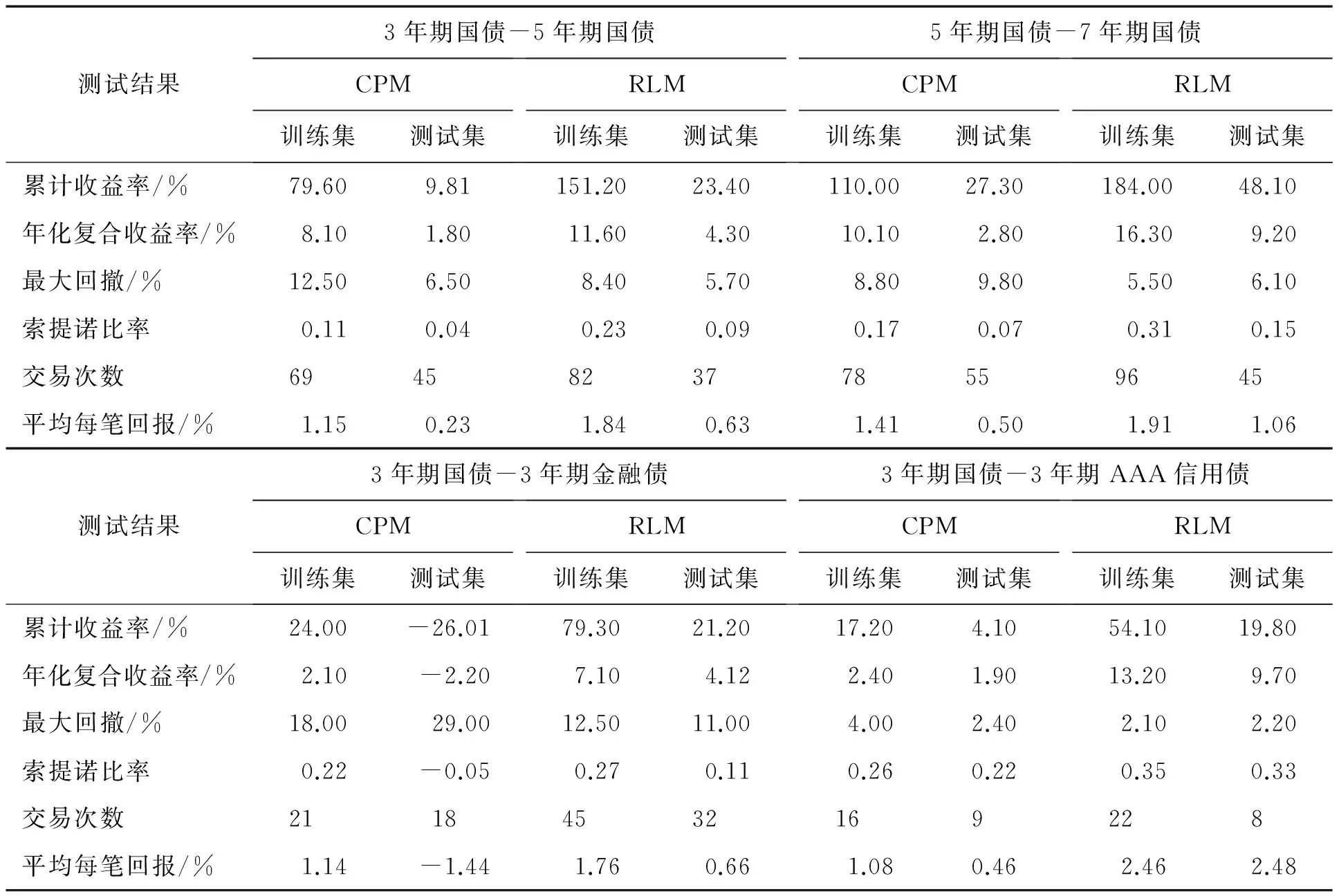
图8 RLM在3年期国债-5年期国债配对组合上的仿真交易(测试集)Figure 8 RLM Simulated Trading on 3Y Treasury-5Y Treasury Pair(out Sample)

表4 CPM和RLM收益率差异的显著性检验Table 4 Significance Tests for the Performance Difference Between CPM and RLM

注：**为在0.050水平上显著，***为在0.010水平上显著。

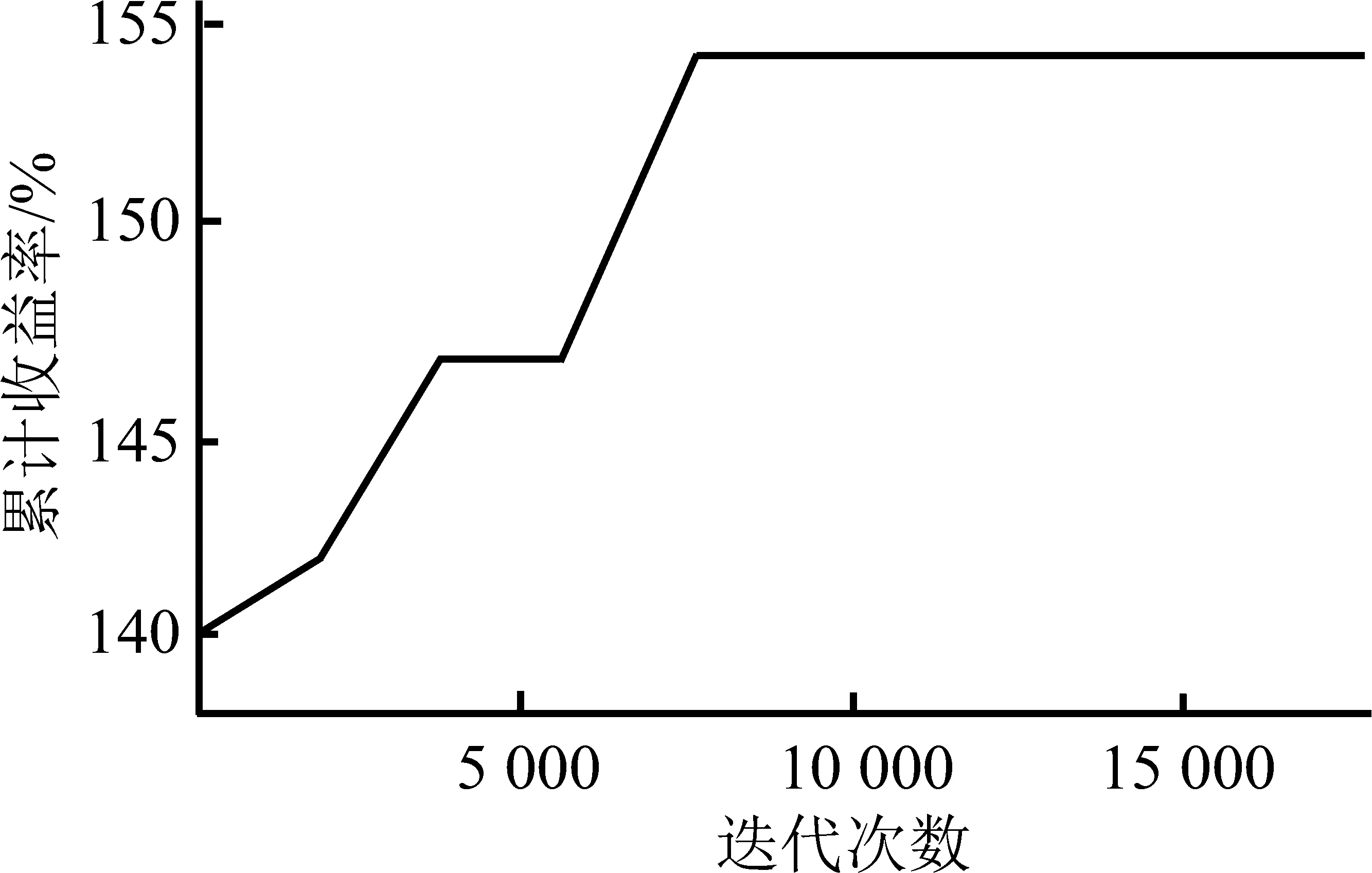
图9 RLM在3年期国债-5年期国债配对组合测试集上的学习过程Figure 9 Learning Process of RLM on 3Y Treasury-5Y Treasury in Sample Data

4.3局限和展望

①受到样本条件的限制，虽然选择中国市场上交易量最大的5种债券作为研究对象，但研究数据未能覆盖更多债券品种，尤其是低级债，这将令本研究结论具有一定的局限性，未来研究可以进一步对更多债券进行全面检验；②本研究采用一种指标作为投资组合绩效的评定标准，未来研究可以尝试多种指标，以进一步明确研究结论的适用范围；③本研究对交易模型初始参数采取的是主观设定，虽然自适应模型的最大特点就是自动优化参数，但若未来研究能对初始参数进行高效初选，将有助于提高模型的收敛速度。

[1]吴晓求.证券投资学.北京:中国人民大学出版社,2014:445-492.

WU Xiaoqiu.Securitiesinvestment.Beijing:China Renmin University Press,2014:445-492.(in Chinese)

[2]GATEV E,GOETZMANN W N,ROUWENHORST K G.Pairs trading:performance of a relative-value arbitrage rule.TheReviewofFinancialStudies,2006,19(3):797-820.

[3]GRANGER C W J.Some properties of time series data and their use in econometric model specification.JournalofEconometrics,1981,16(1):121-130.

[4]JOHANSEN S. Statistical analysis of cointegration vectors.JournalofEconomicDynamicsandControl,1988,12(2/3):231-254.

[5]VIDYAMURTHY G.Pairstrading:quantitativemethodsandanalysis.Hoboken,NJ:Wiley,2004:73-136.

[6]HUCK N.Pairs selection and outranking:an application to the S&P 100 index.EuropeanJournalofOperationalResearch,2009,196(2):819-825.

[7]HUCK N.Pairs trading and outranking:the multi-step-ahead forecasting case.EuropeanJournalofOperationalResearch,2010,207(3):1702-1716.

[8]BOTOS B,NAGY L,ORMOS M.Pairs trading arbitrage strategy in the old and new EU member states∥Proceedingsofthe14thInternationalConferenceonFinanceandBanking.Ostrava,2013:21-31.

[9]胡伦超,余乐安,汤铃.融资融券背景下证券配对交易策略研究——基于协整和距离的两阶段方法.中国管理科学,2016,24(4):1-9.

HU Lunchao,YU Lean,TANG Ling.Pairs trading strategy research considering short selling and margin trading:a two-stage approach based on cointegration and distance methods.ChineseJournalofManagementScience,2016,24(4):1-9.(in Chinese)

[10] 赵胜民,闫红蕾.A股市场统计套利风险实证分析.管理科学,2015,28(5):93-105.

ZHAO Shengmin,YAN Honglei.Empirical study on the risk of statistical srbitrage in A-share market.JournalofManagementScience,2015,28(5):93-105.(in Chinese)

[11] 高辉,赵进文.沪深300股指套期保值及投资组合实证研究.管理科学,2007,20(2):80-90.

GAO Hui,ZHAO Jinwen.Empirical research for hedge ratio and shares portfolio of Shanghai-Shenzhen 300 Shares Index Futures.JournalofManagementScience,2007,20(2):80-90.(in Chinese)

[12] LIU L,BOGOMOLOV T.The law of one price and arbitrage on China′s dual-listings.TheInternationalJournalofBankingandFinance,2012,9(2):58-76.

[13] KUO K,LUU P,NGUYEN D,et al.Pairs trading:an optimal selling rule.MathematicalControlandRelatedFields,2015,5(3):489-499.

[14] SONG Q,ZHANG Q.An optimal pairs-trading rule.Automatica,2013,49(10):3007-3014.

[15] LARSSON S,LINDBERG C,WARFHEIMER M.Optimal closing of a pair trade with a model containing jumps.ApplicationsofMathematics,2013,58(3):249-268.

[16] NGO M M,PHAM H.Optimal switching for the pairs trading rule:a viscosity solutions approach.JournalofMathematicalAnalysisandApplications,2016,441(1):403-425.

[17] ZENG Z,LEE C G.Pairs trading:optimal thresholds and profitability.QuantitativeFinance,2014,14(11):1881-1893.

[18] CHARALAMBOUS K,SOPHOCLEOUS C,O′HARA J G,et al.A deductive approach to the solution of the problem of optimal pairs trading from the viewpoint of stochastic control with time-dependent parameters.MathematicalMethodsintheAppliedSciences,2015,38(17):4448-4460.

[19] 陈艳,王宣承.基于变量选择和遗传网络规划的期货高频交易策略研究.中国管理科学,2015,23(10):47-56.

CHEN Yan,WANG Xuancheng.A study on high-frequency futures trading strategy based on variable selection and genetic network programming.ChineseJournalofManagementScience,2015,23(10):47-56.(in Chinese)

[20] 李栋,张文宇.基于FAM-ELM股票价格预测研究.计算机仿真,2014,31(8):209-212,316.

LI Dong,ZHANG Wenyu.Stock price prediction based on FAM and ELM.ComputerSimulation,2014,31(8):209-212,316.(in Chinese)

[21] 李锋刚,骆林,陈亚波,等.求解均值-CVaR投资组合模型的改进粒子群算法.计算机工程与科学,2016,38(9):1870-1877.

LI Fenggang,LUO Lin,CHEN Yabo,et al.An improved particle swarm optimization algorithm for portfolio based on mean-CVaR model.ComputerEngineering&Science,2016,38(9):1870-1877.(in Chinese)

[22] 刘永波.投资组合优化的可行性规则人工蜂群算法.智能系统学报,2014,9(4):491-498.

LIU Yongbo.An artificial bee colony algorithm with the feasibility rule for portfolio investment optimizations.CAAITransactionsonIntelligentSystems,2014,9(4):491-498.(in Chinese)

[23] 欧阳红兵,李进.基于协整技术配对交易策略的最优阈值研究.投资研究,2015,34(11):79-90.

OUYANG Hongbing,LI Jin.The optimal threshold of pairs trading strategy based on co-integration analysis.ReviewofInvestmentStudies,2015,34(11):79-90.(in Chinese)

[24] 唐国强,高伟,覃良文,等.基于切比雪夫不等式的白糖高频数据统计套利.统计与决策,2016,445(1):87-90.

TANG Guoqiang,GAO Wei,TAN Liangwen,et al.The statistical arbitrage strategy of high frequency sugar data based on Chebyshev inequality.Statistics&Decision,2016,445(1):87-90.(in Chinese)

[25] 麦永冠,王苏生.WM-FTBD配对交易建仓改进策略及沪深港实证检验.管理评论,2014,26(1):30-40.

MAI Yongguan,WANG Susheng.WM-FTBD improved pairs trading open strategy and the empirical tests in Shanghai,Shenzhen and Hong Kong stock markets.ManagementReview,2014,26(1):30-40.(in Chinese)

[26] DO B,FAFF R.Does simple pairs trading still work?.FinancialAnalystsJournal,2010,66(4):83-95.

[27] 邵超,范宏.时间参数的设定对配对交易收益率的影响.经济管理学刊,2013,2(5):183-188.

SHAO Chao,FAN Hong.The influence between the time parameters and the return of pairs trading.EconomicManagementJournal,2013,2(5):183-188.(in Chinese)

[28] ALEXAKIS C.Long-run relations among equity indices under different market conditions:implications on the implementation of statistical arbitrage strategies.JournalofInternationalFinancialMarkets,InstitutionsandMoney,2010,20(4):389-403.

[29] 张河生,闻岳春.基于参数调整的协整配对交易策略:理论模型及应用.西部金融,2013,455(1):11-16.

ZHANG Hesheng,WEN Yuechun.The co-integration pairing trading strategy based on the parameter adjustment:the theory model and application.WestChinaFinance,2013,455(1):11-16.(in Chinese)

[30] 李世伟.基于协整理论的沪深300股指期货跨期套利研究.中国计量大学学报,2011,22(2):198-202.

LI Shiwei.Research on the calendar spread arbitrage of CSI 300 stock index futures based on Co integration theory.JournalofChinaUniversityofMetrology,2011,22(2):198-202.(in Chinese)

[31] 彭舒怡.基于GARCH模型银行股配对交易研究.知识经济,2013(5下):61-63.

PENG Shuyi.Research of bank stocks pairs trading based on GARCH model.KnowledgeEconomy,2013(5-3):61-63.(in Chinese)

[32] 何树红,张月秋,张文.基于GARCH模型的股指期货协整跨期套利实证研究.数学的实践与认识,2013,43(20):274-279.

HE Shuhong,ZHANG Yueqiu,ZHANG Wen.Empirical study on calendar spread arbitrage of CSI 300 stock index futures based on cointegration theory and GARCH model.MathematicsinPracticeandTheory,2013,43(20):274-279.(in Chinese)

[33] 刘阳,李艳丽, 陆贵斌.基于信息更新NN-GARCH模型的统计套利研究.统计与决策,2016,445(2):169-171.

LIU Yang,LI Yanli,LU Guibin.Research of statistical arbitrage strategy based on NN-GARCH model.Statistics&Decision,2016,445(2):169-171.(in Chinese)

[34] 邢恩泉,尹涛.协整模型的配对交易策略优化.经济数学,2015,32(1):65-69.

XING Enquan,YIN Tao.The improvements in pairs trading strategy of the cointegration model:ergodic research on the basis of computer technology.JournalofQuantitativeEconomics,2015,32(1):65-69.(in Chinese)

[35] SILVER D,HUANG A,MADDISON C J,et al.Mastering the game of Go with deep neural networks and tree search.Nature,2016,529(7587):484-489.

[36] SUTTON R S,BARTO A G.Reinforcementlearning:anintroduction.Cambridge,MA:MIT Press,1998:42-56.

[37] LEE J W,PARK J,JANGMIN O,et al.A multi-agent approach toQ-learning for daily stock trading.IEEETransactionsonSystems,Man,andCybernetics,PartA:SystemsandHumans,2007,37(6):864-877.

[38] TAN Z,QUEK C,CHENG P Y K.Stock trading with cycles:a financial application of ANFIS and reinforcement learning.ExpertSystemswithApplications,2011,38(5):4741-4755.

[39] 李静静.基于模糊K均值聚类和Sarsa(λ)算法的自适应爬壁机器人路径规划.计算机测量与控制,2014,22(9):2879-2881,2885.

LI Jingjing.Adaptive path planning of wall-climbing robot based on MIP and improved fuzzyK-means algorithm and Sarsa(λ).ComputerMeasurement&Control,2014,22(9):2879-2881,2885.(in Chinese)

[40] 戈军,周莲英.基于SARSA(λ)的实时交通信号控制模型.计算机工程与应用,2015,51(24):244-248.

GE Jun,ZHOU Lianying.Real-time traffic signal control model based on SARSA(λ).ComputerEngineeringandApplications,2015,51(24):244-248.(in Chinese)

[41] 刘小峰,陈国华,李真.零售网络的结构建模与演化分析.管理科学,2009,22(4):23-30.

LIU Xiaofeng,CHEN Guohua,LI Zhen.The structure of the retail networks:simulation modeling and evolution analysis.JournalofManagementScience,2009,22(4):23-30.(in Chinese)

[42] 石春生,梁洪松.组织运作过程中的自适应机理.管理科学,2004,17(1):12-16.

SHI Chunsheng,LIANG Hongsong.Self-adaptation mechanism in the organizational process.JournalofManagementScience,2004,17(1):12-16.(in Chinese)

FundedProject:Supported by the National Natural Science Foundation of China(71571048)

Biography:HU Wenwei, doctor in management, is an associate professor in the School of Management at Shanghai University of Engineering Science. Her research interests include financial engineering and securities investment. Her representative paper titled “Pricing value difference between barrier and vanilla options with binomial pricing method” was published in theJournalofShanghaiJiaotongUniversity(Issue 5, 2012). E-mail：huwenwei@sues.edu.cn

HU Jianqiang, doctor in management, is a professor in the School of Management at Fudan University. His research interest includes financial mathematics. His representative paper titled “Efficient simulation resource sharing and allocation for selecting the best” was published in theIEEETransactionsonAutomaticControl(Issue 4, 2013). E-mail：jqhu@fudan.edu.cn

LI Zhan, doctor in management, is a professor in the Institute of Applied Economics at Shanghai Academy of Social Sciences. His research interest includes investment management. His representative paper titled “A comparative research of average risk of portfolio on different strategies and risk diversification” was published in theJournalofShanghaiJiaotongUniversity(Issue 12, 2011). E-mail：zli@sjtu.edu.cn

ZHOU Jianfeng, is an investment manager in the Fixed-income Division at Guotai Junan Securities Group. His research interest includes quantitative investment. E-mail：zhoujianfen012977@gtjas.com

□

Self-adaptivePairsTradingModelBasedonReinforcementLearningAlgorithm

HU Wenwei1，HU Jianqiang2，LI Zhan3，ZHOU Jianfeng4

1 School of Management, Shanghai University of Engineering Science, Shanghai 201620, China2 School of Management, Fudan University, Shanghai 200433, China3 Institute of Applied Economics, Shanghai Academy of Social Sciences, Shanghai 200020, China4 Fixed-income Division, Guotai Junan Securities Group, Shanghai 200120, China

Pairs trading is one of the major statistical arbitrage trading strategies. However, its profit opportunity has become scarcer due to the improvement of the market efficiency. The traditional fixed parameter trading models are no longer sufficient for eternal profit maximization. The parameters of the trading models need not only to be optimized but also to be done so dynamically in an automatic manner. Therefore, it is necessary to develop a trading model of which parameters are dynamically optimized with artificial intelligence, as it may be of significance in improving the profitability and efficiency of trading models.

A new type of statistical arbitrage trading model is proposed based on the reinforcement learning mode, improving the traditional cointegration trading strategy; Applying the Sarsa algorithm andε-greedy strategy to the new model, the key parameters in the new trading model can self-adapt to reach the optimal values, instead of judging from professional experience or insisting on determined parameters just like the traditional strategy; A computer simulation is designed to run through the complete process of the new trading model including model parameters self-adapting adjustment, securities transaction, and trading performance evaluation. The trading simulation and empirical tests such as Johansen cointegration test, t-test, and Robustness test are conducted on four bond pairs that are composed of the top five bonds with the largest trading volumes in the mainland markets.

The results show that the new model outperforms the traditional one in all aspects. It significantly enhances the profitability of the trading system while reducing the drawdown risks; It improves the efficiency of arbitrage trading as it reduces the number of transactions and thus transaction costs; It possesses ability to learn continuously so that it increases the accumulated return step by step and eventually converges to the highest level. The results also reveal that the cointegration trading strategy is efficient in the Chinese bond markets.

The new model unprecedentedly adapts reinforcement learning to pairs trading, realizing the self-adapted adjustment of the model parameters. The improved model is helpful to halt the decrease in the profitability of the traditional pairs trading strategy. It may provide a new powerful arbitrage tool for investors in the Chinese markets, who now may have already adopted the short sale tools like stock index futures and margin trading.

cointegration pairs trading；Sarsa reinforcement learning algorithm；self-adaption；dynamic parameters；optimization；simulation；statistical arbitrage

Date:August 10th, 2016AcceptedDateJanuary 25th, 2017

F830.9

A

10.3969/j.issn.1672-0334.2017.02.012

1672-0334(2017)02-0148-13

2016-08-10修返日期2017-01-25

国家自然科学基金(71571048)

胡文伟，管理学博士，上海工程技术大学管理学院副教授，研究方向为金融工程和证券投资等，代表性学术成果为“基于二叉树方法的障碍期权与标准期权价差分析模型”，发表在2012年第5期《上海交通大学学报》，E-mail：huwenwei@sues.edu.cn

胡建强，管理学博士，复旦大学管理学院教授，研究方向为金融数学等，代表性学术成果为“Efficient simulation resource sharing and allocation for selecting the best”，发表在2013年第4期《IEEE Transactions on Automatic Control》，E-mail：jqhu@fudan.edu.cn

李湛，管理学博士，上海社会科学院应用经济研究所教授，研究方向为投资管理等，代表性学术成果为“不同策略条件下的投资组合平均风险比较与分散”，发表在2011年第12期《上海交通大学学报》，E-mail：zli@sass.org.cn

周剑峰，国泰君安证券公司固定收益部经理，研究方向为量化投资等，E-mail：zhoujianfen012977@gtjas.com