矩阵方程的一个二次收敛迭代算法*

刘 健，孙洪春

(1.鲁南技师学院信息工程系，山东 临沂 276021；2. 临沂大学数学与统计学院，山东 临沂 276005)

矩阵方程的一个二次收敛迭代算法*

刘 健1，孙洪春2

(1.鲁南技师学院信息工程系，山东 临沂 276021；2. 临沂大学数学与统计学院，山东 临沂 276005)

提出了求解一类矩阵方程的一个收敛算法, 在较宽松的条件下, 证明了所给算法的全局收敛性和二次收敛率,也给出了算法的数值试验,试验表明算法是有效的.

矩阵方程；全局收敛性；二次收敛率

引言

考察的矩阵方程是：

(1)

其中Ai∈Cm×p,Bi∈Cq×n,C∈Cm×n为已知矩阵,X∈Cp×q为未知矩阵.为叙述方便，令

(2)

F(X):Cpq→Cmn.在本文中,假设方程(1)的解集非空,记为Ω*.

矩阵方程是代数学中重要的问题之一, 广泛应用于计算数学、量子力学、计算机安全、自动控制理论、系统识别、振动理论、图像处理等.近年来，无论在实际背景应用还是在学术前景研究方面，矩阵方程解的存在性和求解算法的设计已成为数值代数研究的一个热门课题，引起了国内外许多学者浓厚的研究兴趣.Xu等[1]给出了矩阵方程最小二乘解的表达式和解的存在唯一性的充分必要条件. Sheng等[2]提出了求解矩阵方程的对称解和斜对称解的两种有效的迭代方法. Liao等[3]给出了矩阵方程的一种最小二乘解的最小范数解析表达式，并给出了求解该类解的算法和数值实验. Peng[4]提出了两种求解矩阵方程的迭代方法，相比较该迭代方法的收敛速度更快、精度更高. Liao[5]基于广义奇异值分解探讨了半正定矩阵集上的矩阵方程最小二乘解. 彭亚新[6]用迭代法研究了矩阵方程AXB=F的一般解、对称解、(反)中心对称解、双对称解与对称次反对称解等问题. Li等[7]基于Moore-Penrose逆和Kronecker积，提出了求解矩阵方程解的一般表达式和相应的数值算法. 本文提出了求解矩阵方程的一个新矩阵迭代算法, 在较宽松的条件下, 证明了所给算法的全局收敛性和二次收敛率，也给出了算法的数值试验,试验表明算法是有效的.

本文所用符号含义：用‖·‖ 表示向量的2范数，‖·‖F表示矩阵的Frobenius范数，dist(X,Ω*)表示矩阵X到解集Ω*的最近距离，AT表示矩阵A的转置.

1 预备知识

为分析所给下面迭代算法， 回顾如下的一些知识.

定义1 设矩阵A=(aij)m×n∈Rm×n,B=(bij)s×t∈Rs×t, 则A和B的Kronecker积定义为

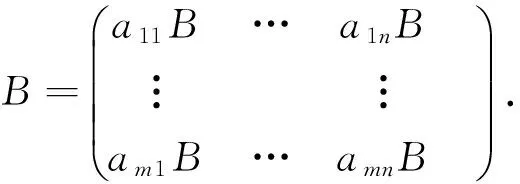
定义2 设矩阵A=(aij)m×n∈Rm×n， 则A的拉直就是按矩阵A的列的先后顺序进行上下叠放，记为vec(A)，即

对于以上两种运算，有以下性质.

命题1 对可乘矩阵A,B,C,D,下述结论成立

(A1) (A⊗B)T=AT⊗BT； (A2) vec(ABC)=(CT⊗A)vec(B)

由式(2)和命题1的(A2)知:

(3)

vecF(X)=AvecX-vecC=0

(4)

因此，Ω*和Ω是等价的，其中Ω={vecX∈Rpq|AvecX=vecC}.

设矩阵M,N∈Rm×n,定义矩阵的内积为:

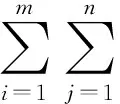
因此，可定义矩阵M∈Rm×n的Frobenius范数：

(5)

命题2 对于集合W={x∈Rn|Dx=d}，D∈Rl×n,d∈Rl. 则

PW(x)=(I-D+D)x+D+d, ∀x∈Rn,

式中PW(x)是向量x∈Rn在集合W上的投影，D+是矩阵D的广义逆.

由命题2，结合(4)可得:

(6)

根据式(5)的定义，可得:

dist(X,Ω*)≤‖A+‖‖F(X)‖F

(7)

还可得到如下性质. 基于(3)，容易得vecF′(X)=A. 对于(4)，有:

(8)

式中a>0为常数.

∀X,Y∈Rpq.由(3)得：

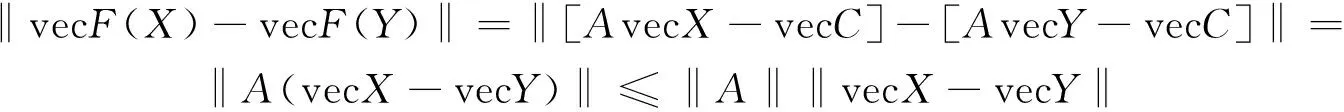
(9)

再根据(5)的定义方式，∀X,Y∈Rpq.进一步可得：

(10)

2 算法和收敛性

本节，给出解(1)的一个新矩阵迭代算法，基于预备知识中的分析，证明所给算法的全局收敛性和二次收敛率.

算法1

第一步:选择参数ε≥0，初始点X0∈Rp q. 令k=0.

第二步:若‖F(Xk‖)≤ε，停止；否则，转第三步 3.

第三步:求方程组的解Dk作为在点Xk处的一个搜索方向

(ATA+μkI)vecDk=-ATvecF(Xk)

(11)

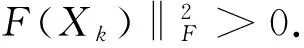
下面，给出算法1的收敛性和收敛率分析. 首先分析算法1的可行性.

对于方程(11)，由μk>0，则矩阵(ATA+μkI)是正定的，所以(11)有唯一解Dk. 而且vecDk也是下面无约束优化的一个下降方向，

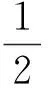
(12)

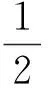
▽φ(Xk)TvecDk=[vec′F(Xk)TvecF(Xk)]TvecDk=-[ATvecF(Xk)]T(ATA+μkI)-1[ATvecF(Xk)]<0.

定义θk(D)=‖AvecD+vecF(Xk)‖2+μk‖vecD‖2，函数θk为严格凸函数,因此,无约束极小化问题

minθk(D)

(13)

等价于(11). 事实上，

▽θk(Dk)=2AT[AvecDk+vecF(Xk)]+2μkvecDk=2[ATA+2μkI]vecDk+2ATvecF(Xk)=0.

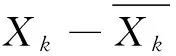
引理1 对于算法1产生的Xk,X*∈Ω*，则由(11)求得的解Dk满足

‖Dk‖≤dist(Xk,Ω*)

(14)

‖AvecDk+vecF(Xk)‖≤c1dist2(Xk,Ω*)

(15)

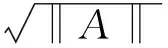
证明 因为vecDk是最小化问题(13)的解,从而有：

(16)

根据θk的定义及(16)、(8)有：

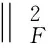
同理可证第二个不等式

3.1.4 猪的室间隔缺损模型 这类模型非常重要，由于这类疾病模型属于自然发生，能够有效模拟人类收缩功能正常的心力衰竭模型[18-19]。

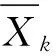
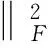
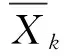
引理2 对于算法1产生的Xk-1,Xk,有:

dist(Xk,Ω*)≤c2dist2(Xk-1,Ω*)

(17)

式中c2=c1‖A+‖.

证明 由式(8)得

0 = ‖vecF'(Xk-1)vecDk-1-(vecF(Xk-1+Dk-1)-vecF(Xk-1))‖≥

‖vecF(Xk-1+Dk-1)‖-‖vecF'(Xk-1)vecDk-1+ vecF(Xk-1)‖

即‖vecF(Xk-1+Dk-1)‖≤‖vecF'(Xk-1)vecDk-1+ vecF(Xk-1)‖.再由Xk=Xk-1+Dk-1知：

dist(Xk,Ω*) = dist(Xk-1+Dk-1,Ω*)≤‖A+‖‖F(Xk-1+Dk-1)‖F=

‖A+‖‖vecF(Xk-1+Dk-1)‖≤‖A+‖‖AvecDk-1+ vecF(Xk-1)‖≤c1‖A+‖dist2(Xk-1,Ω*).

式中第一个不等式是根据式(7)而得，最后不等式成立是因为式(15).令c2=c1(A+),有式(17)成立.

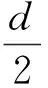
证明 首先证明l=1时结论成立.

‖X1-X*‖≤‖X0+D0-X*‖ ≤‖X0-X*‖ + ‖D0‖ ≤

‖X0-X*‖ + dist(X0,Ω*) ≤‖X0-X*‖ + ‖X0-X*‖ ≤2r.

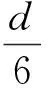
(18)

再由(13)式得：

(19)

于是有：

(20)

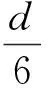
基于以上引理,下面给出点列{Xk}的收敛定理.

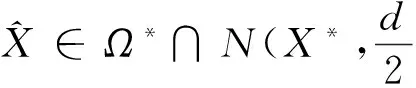
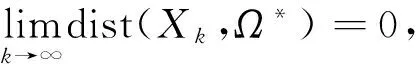
{dist(Xk,Ω*)}二次收敛于0.

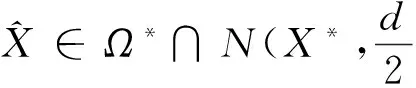
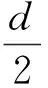
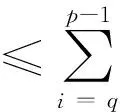
从而{Xk}为柯西点列, 因此点列{Xk}收敛.

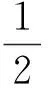
算法2

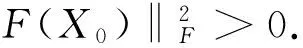
第二步: 若‖F(Xk)‖≤ε，停止；否则，转第三步.

第三步: 求下面方程组的解Dk使得(ATA+μkI)vecDk=-ATvecF(Xk).

若

‖F(Xk+Dk)‖F≤γ‖F(Xk)‖F

(21)

第四步: 令mk是使得下面不等式成立的最小非负整数m,

φ(Xk+βmDk)-φ(Xk)≤αβm▽φ(Xk)TDk

(22)

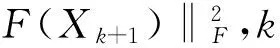
下面，给出算法2的全局收敛性和二次收敛率.

定理2设{Xk}是算法2产生的序列,则序列{Xk}的任一聚点都是方程(12)的解,即是方程(1)的解. 进一步有{dist(Xk,Ω*)}二次收敛于0.

证明假设方程(12)在Xk点的稳点▽φ(Xk)≠0, 则ATvecF(Xk)≠0, 又由(11)知Dk≠0, 且

▽φ(Xk)TvecDk=[vec′F(Xk)TvecF(Xk)]TvecDk=-[vecDk]T(ATA+μkI)-1[vecDk]<0.

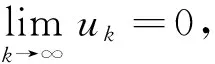
▽φ(Xk)TvecDk=[vec′F(Xk)TvecF(Xk)]TvecDk

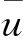
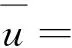
(1-βmk)‖(ATA+μkI)-1AT‖≤c2‖A‖‖A+‖

(21)

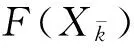
(22)

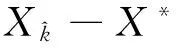
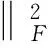
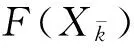
3 数值试验

下面给出算法1的数值试验,实验表明所提算法是有效的.

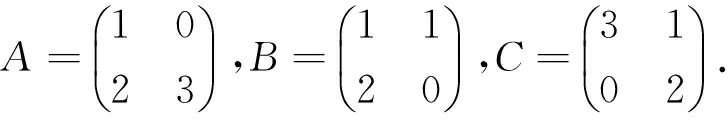
例2 令F(X)=AXB-C=0, 其中:

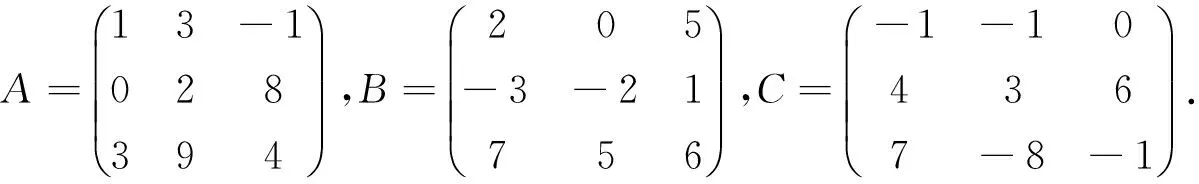
此时‖F(X*)‖F=5.9669e-014.

[1]Xu Guiping, Wei Musheng, Zheng Daosheng. On solutions of matrix equation.AXB+CYD=F[J]. Linear Algebra and its Applications, 1998, 279: 93-109.

[2]Sheng Xingping, Chen Guoliang. An iterative method for the symmetric and skew symmetric solutions of a linear matrix equationAXB+CYD=E[J]. Journal of Computational and Applied Mathematics, 2010, 233: 3030-3040.

[3]Liao Anping, Lei Yuan. Least-Squares Solution with the Minimum-Norm for the Matrix Equation (AXB,GXH)=(C,D)[J]. Computers and Mathematms with Apphcatmns, 2005 ,50: 539-549.

[4]Peng Zhenyun. New matrix iterative methods for constraint solutions of the matrix equationAXB=C[J]. Journal of Computational and Applied Mathematics, 2010, 235:726-735.

[5]Liao A P, Bai Z Z. Least squares solutions ofAXB=Dover symmetric positive semidefinte mareices [J]. Journal of Computational Mathematics. 2003,21(2):175-182.

[6]彭亚新.求解约束矩阵方程及其最佳逼近的迭代法研究[D]. 长沙: 湖南大学数学与计量经济学院, 2004.

[7]Li Hongyi, Gao Zongsheng, Zhao Di. Least squares solutions of the matrix equationAXB+CYD=Ewith the least norm for symmetric arrowhead matrices[J]. Applied Mathematics and Computation, 2014, 226(1): 719-724.

[8]程云鹏，矩阵论[M].西安：西北工业大学出版社，1999.

[9]王宜举，修乃华.非线性最优化理论与算法[M].北京:科学出版社, 2016.

[10]Facchinei F. Minimization of SC1 functions and the Maratos effect [ J ]. Operations Research Letters, 1995, 17(3):131-137.

AQuadraticConvergenceIterativeAlgorithmforMatrixEquations

LIU Jian1, SUN Hong-chun2

(1.Department of Information Engineering, Lunan Technician University, Linyi Shandong 276021, China;2. School of Mathematics and Statistics, Linyi University, Linyi Shandong 276005, China)

This paper presents a convergence algorithm to solve matrix equations. Under relaxed conditions, the global convergence and quadratic convergence rate of the given algorithm are proved. The numerical experiment is also given to show that the algorithm is effective.

matrix equations; global convergence; quadratic convergence rate

1673-2103(2017)05-0001-06

2017-08-05

国家自然科学基金项目(11671228)；中国物流学会与中国物流与采购联合会计划项目 (2015CSLKT3-199)

刘健(1968-)，男，山东临沂人，副教授，研究方向：最优化算法及其应用.

孙洪春(1968-), 男, 山东费县人, 教授, 硕士，研究方向：最优化理论与算法.

O 221

A