基于对角递归神经网络的小区用电负荷预测研究

徐建军 杜蔷楠 闫丽梅

(东北石油大学电气信息工程学院)

基于对角递归神经网络的小区用电负荷预测研究

徐建军 杜蔷楠 闫丽梅

(东北石油大学电气信息工程学院)

为了提高小区用电负荷预测的准确度，在研究对角递归神经网络的基础上，分析比较几种优化算法，提出基于粒子群算法的对角递归神经网络预测方法。通过对小区用电负荷影响因素的分析以及对大量历史数据进行训练，最后经Matlab仿真分析，结果表明：该方法预测的准确度较高。

对角递归神经网络 用电负荷预测 粒子群算法

负荷分析是实现当地电力规划的前提和基础，尤其对研究小区用电负荷的变化趋势和特点具有重要意义。小区用电负荷预测按照预测期限可以分为即期预测(日或周)、短期预测(12～24个月)、中期预测(5～10年)和长期预测(10～30年)[1]。笔者对小区用电负荷的预测属于短期预测。长期以来，中外学者以及相关的电力工作人员在丰富的研究与实际工作中积极探索精确度更高、效果更好的用电负荷预测方法，主要分为传统的数学统计类预测方法和新型的人工智能预测方法。

人工神经网络(Artificial Neural Network，ANN)是采用数学手段来模拟人类大脑或生物神经元网络的非线性系统，包含了大量人工神经元，每个简单的神经元通过不同的拓扑结构组合，形成的神经网络却十分复杂，功能也变得很强大。它通过比较多个不相关的因子来得到最佳的参数，用于分析自变量与因变量两者的联系，它的优势在于能够很好地解决非线性问题，即使在学习的过程中出现了特殊情况，增加了特殊变量，这些都不影响它的学习能力，反而能够使得最优参数经过对比学习后得到进一步的优化和调整。所以将ANN技术运用到电力负荷预测中十分适合。它不需要假定输入变量的相关信息，也无需依靠专家经验，仅利用现有数据即可通过训练抽取和逼近输入输出之间隐含的非线性关系[2]。

1 对角递归神经网络

对角递归神经网络(Diagonal Recurrent Neural Network，DRNN)是一种反馈神经网络，它依赖神经元之间内部的反馈来描述动态行为，使神经网络具有反馈的性能，且能生动形象地反映出系统的动态特性，不用存储所有的输入信息，用较少的记忆单元就可反映出非线性系统的动力学特性[3]。

1.1DRNN模型结构

DRNN神经网络算法可表示为：

(1)

Xj(k)=f(Sj(k))

(2)

(3)

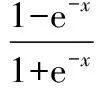
(4)

DRNN神经网络辨识结构如图1所示[4]。图中k是网络的迭代步数，DRNN为网络辨识器，u(k)为辨识器的输入，y(k)为被控对象实际输出，ym(k)为DRNN的输出结果，将y(k)和u(k)的差值作为DRNN的调整信号，则有：

逼近误差e(k)=y(k)-ym(k)

(5)

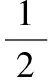
(6)

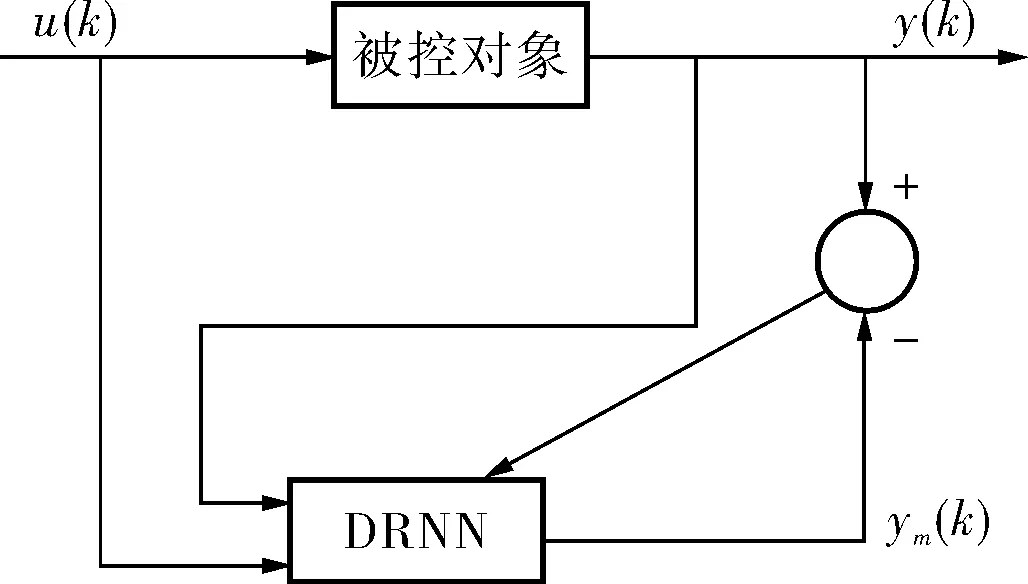
图1 对角递归神经网络结构

1.2BP算法训练DRNN网络

神经网络中应用最为常见的是BP算法。该算法的学习规则是最小均方误差准则，学习过程由正反向传播共同组成。正向传播指的是信号经过一系列的分析计算，最后在输出端得到了正确的结果，如果结果错误，则开始反向传播，即将前面所得的结果和期望结果作差处理后作为反向的输入信号，反过来从输出端输入。

假设一个非线性系统的数学模型为：

(7)

输入信号为：

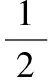
(8)

这里笔者所用到的对角神经网络的拓扑结构为2-7-1，即两个输入神经元，7个中间隐含层神经元，一个输出神经元；迭代次数为100，采样频率为1kHz，学习速率设为0.35，最后加入动量因子α来调整，α=0.1。

测试信号为：

u(k)=0.7sin(4πkt/25)+0.3sin(4πkt/1000)

(9)

采用BP算法训练对角递归神经网络的具体步骤为：

a. 初始化各项基本参数，提供足够的样本。

b. 正向传播计算，得到该过程中各层网络参数值。

c. 根据式(5)计算逼近误差。

d. 根据权值调整算法调整各层网络的权值。

e. 判断步骤d所得的误差精度是否合格。

f. 如若符合要求，将权值保存起来并且训练到此结束；如果不符合要求，则返回步骤b重新开始下一轮计算。

仿真结果如图2所示，从图中可以看出，虚线的逼近输出随着迭代次数的增多，出现逐渐偏离实际输出(实线)的现象，尤其是峰顶毛刺突出极为严重，总体效果一般。逼近误差图(图3)表明，毛刺出现在中间的概率较大，当迭代次数接近100时，均方差几乎收敛于0.000 1。这主要是由于训练初期各项参数的初始值选取不当，使网络辨识不稳定，参数的正确与否是DRNN的核心问题，初始权值的选择会对DRNN的性能产生很大影响，所以笔者采用粒子群算法来优化对角递归神经网络。

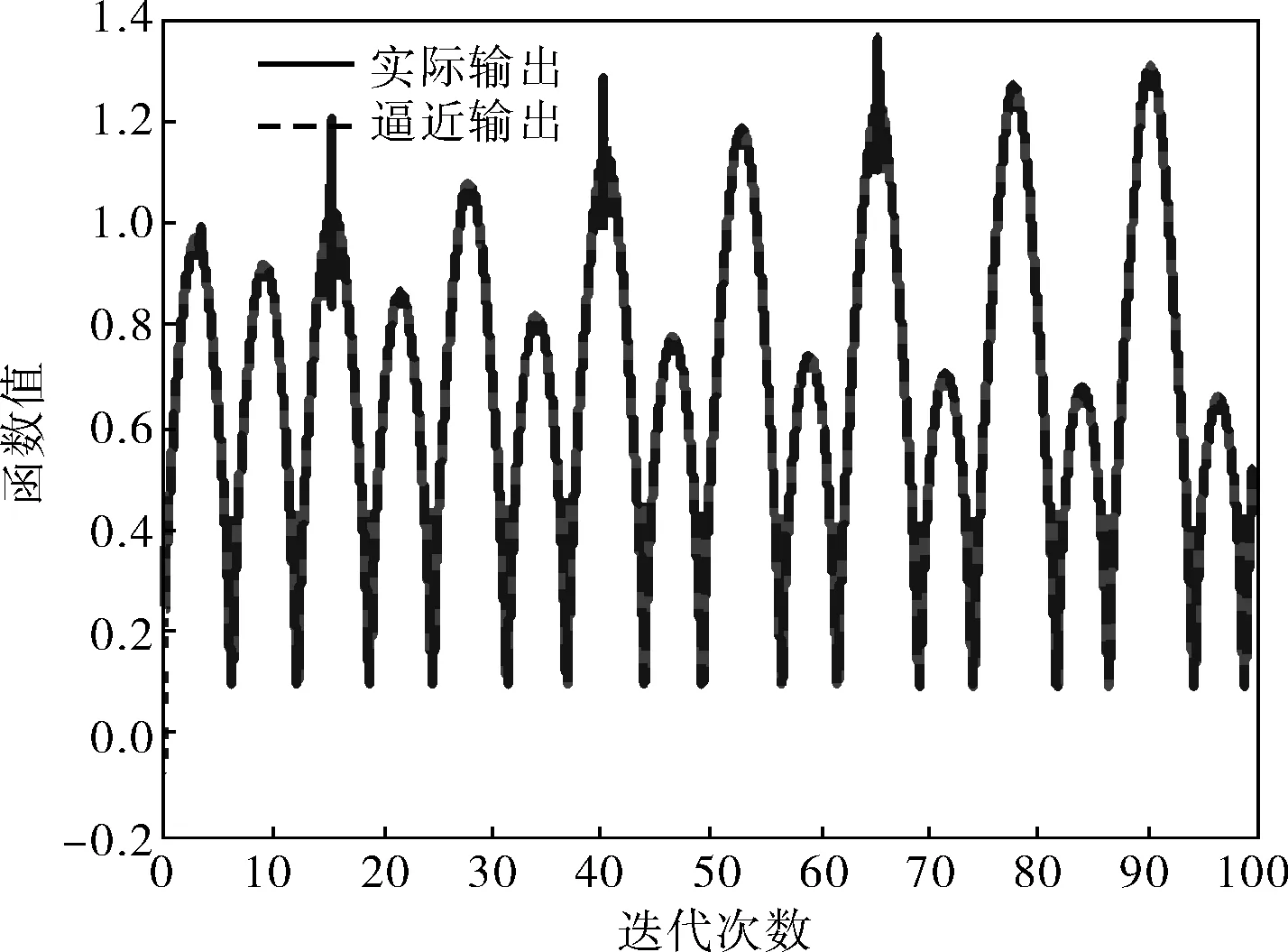
图2 BP训练DRNN网络的仿真结果

图3 BP训练DRNN网络的逼近误差

2 粒子群优化算法

粒子群优化算法(Particle Swarm Optimizer，PSO)作为一种全局优化算法，它的基础是迭代模式，这种算法通过鸟群的觅食来体现，鸟群外出集体觅食时，往往有一只头鸟带头，其他的鸟跟着头鸟，当头鸟找到食物后，通过动物独特的方式将信息发给鸟群，鸟群收到信息后就会朝着头鸟的方向靠近，最终到达目的地，与头鸟汇合。

2.1粒子群算法运算流程

根据外部变化的因素，随时修正移动的方向和速度，通过不断地搜索与修正，以寻找最佳的目标。每进行一次计算，粒子根据个体极值pbest寻找出最佳个体，并继续进行重复计算迭代，个体极值寻找出全体极值gbest，此时找到目标，完成迭代过程，具体计算迭代公式如下：

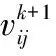
(10)

(11)

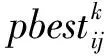
a. 粒子群初始化。任意产生的m维粒子(x1,x2,…,xm)作为最初的起始种群X(t)；各粒子初始速度定义为以(vi1,vi2,…,vim)构成的速度矩阵V(t)。

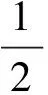
c. 调整惯性权重ω。将每一个粒子适应值和上一步的最佳个体值作出对比，若是当前粒子的适应值更好，则用当前粒子适应值代替个体最优值pbest并修改ω；同时，将该粒子的适应值和全体最优值进行比较，如果前者更好，也替换全体最优值并修改ω。

e. 停止条件。当粒子适应度达到预先要求的精度或者迭代结束时，停止迭代，反之跳转到步骤b继续迭代。

2.2粒子群算法寻优性能测试

寻优算法的寻优能力、性能是衡量这个算法是否可行的关键标准。首先针对常用的优化算法进行分析比较，这里选取遗传算法(GA)和蚁群算法(ACO)与粒子群算法进行寻优性能测试对比。通常的方法是选取测试函数来进行测试，笔者选择rosenbrock函数：

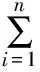
(12)

|xi|≤30 min(f(x))=0

迭代次数设为1 000，粒子每一维数的最大值为30，最小值为-30，学习因子c1、c2为2，惯性权重ω为0.5。仿真测试后得出的对比结果如图4所示。

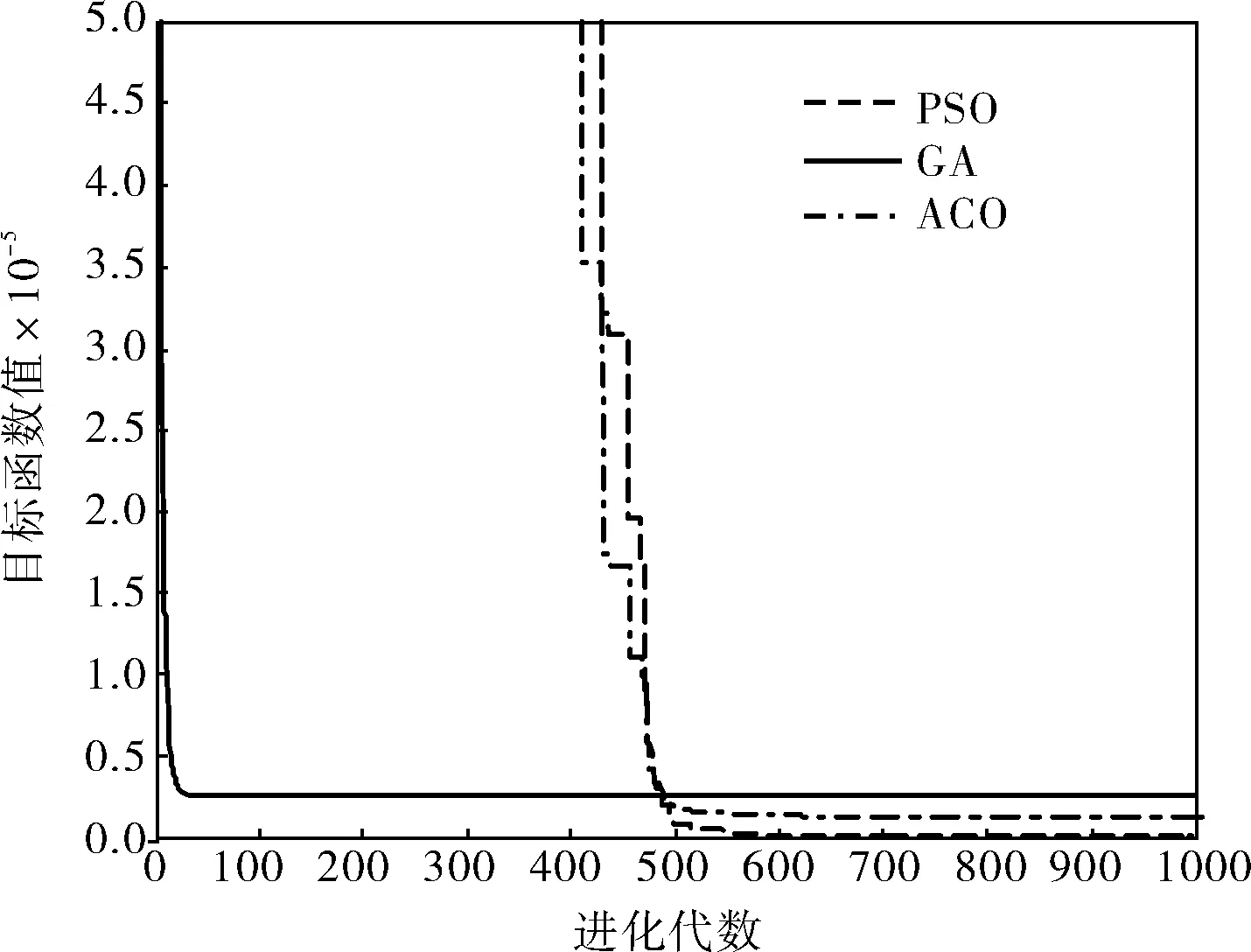
图4 rosenbrock测试函数性能对比

仿真结果显示对于rosenbrock函数,PSO寻优的最优目标值为5 607.4，GA寻优的结果为25 700.0，同时ACO的结果为10 832.5。从各方面来看仍然是PSO全面占优。

从上述测试函数的仿真对比来看，PSO在寻优精度和全局寻优能力上都是完全领先GA和ACO的，并且不会陷入局部最优。因此笔者采用PSO优化DRNN是完全科学可取的。

3 基于PSO-DRNN网络的模型在小区用电负荷预测中的应用

前文已经确立了基于粒子群算法的对角递归神经网络的预测方法，在进行预测前，要先考虑各种不确定因素对用电负荷的影响，分析每个因素的相关性特点以及对用电负荷影响所占的权重比例，为后面更精确地进行负荷预测奠定基础。

根据分析，影响小区用电负荷的因素有许多，把影响因素归纳为以下几个方面：人口因素、经济收入因素、季节因素、节假日因素、电器因素和电价因素，这些因素对小区用电负荷都会产生或多或少的影响。笔者将这6个因素作为影响小区用电量的因素数据，与所采集的历史数据一起进行训练。训练样本采用2015年某些天的用电量数据。

图5为模型建立的流程。图6为粒子群优化算法的适应度曲线(c1=1.5,c2=1.7,种群数量为20)。从曲线中可以发现，适应度曲线在全局都有不断的收敛，说明粒子群通过不断改变位置使得适应度更优，从而得到更优的网络权值。

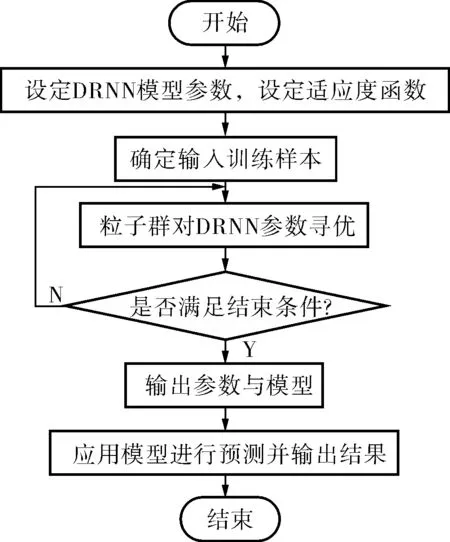
图5 粒子群优化对角递归神经网络建模流程

图6 粒子群优化对角递归神经网络适应度曲线

将2016年度的数据输入到对角神经网络模型中预测该小区每个月份的用电量，预测效果如图7所示，反映了该小区一年中每个月的用电量变化，测试的误差精度对于用电量的数量等级来说已经很低了，可以作为工作中评估用电量的参考。

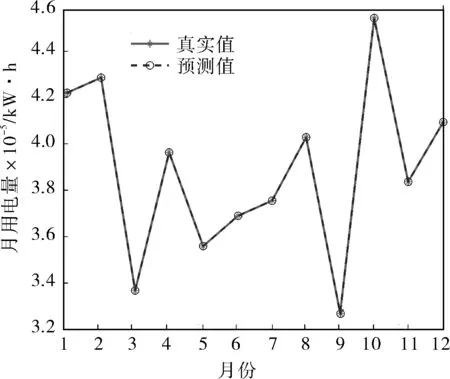
图7 基于PSO-DRNN模型预测某小区一年用电量对比

4 结束语

笔者提出基于对角递归神经网络的用电负荷预测方法，通过3种优化算法的对比，选定了全局寻优能力最好的粒子群算法来优化对角递归神经网络。经实例验证，基于PSO-DRNN的预测模型能够通过训练历史数据预测未来一段时间内小区的用电量变化情况，可以认为笔者建立的PSO-DRNN模型对于小区的用电负荷预测有较好的效果。

[1] 林承就.福州市住宅小区用电负荷计算的研究[D].长沙：中南大学，2008.

[2] 王乐.基于灰色理论和神经网络的电力系统短期负荷预测研究及其比较[D].南宁：广西大学，2012.

[3] 龚文杰，段晓燕，张智晟.基于分布估计算法的对角递归神经网络短期负荷预测模型研究[J].青岛大学学报，2012，27(2)：43～47.

[4] 戴晟.基于DE算法的DRNN网络非线性系统辨识研究[D].成都：西南交通大学，2011.

ResearchonPowerLoadForecastingofResidentialDistrictsBasedonDiagonalRecurrentNeuralNetwork

XU Jian-jun, DU Qiang-nan, YAN Li-mei

(CollegeofElectricalEngineeringandInformation,NortheastPetroleumUniversity)

In order to improve the accuracy of predicting power consumption of residential districts, having the study of diagonal recurrent neural network based to analyze and compare several optimal algorithms was implemented, including the proposal of diagonal recurrent neural network predicting method based on the particle swarm algorithm. Analyzing the factors which influencing the power consumption of residential districts and the training a large number of historical data and Matlab simulation show that, this predicting method has higher accuracy.

diagonal recurrent neural network, power consumption prediction, particle swarm optimization

黑龙江省自然科学基金项目(E2017011)。

徐建军(1971-),教授, 从事电力理论与新技术的研究。

联系人闫丽梅(1971-)，教授，从事电力系统安全稳定分析与控制的研究，565735794@qq.com。

TP18

A

1000-3932(2017)11-1052-05

2017-06-16，

2017-09-19)