一类二阶中立型Emden-Fowler方程的振动条件

于海芳，韩 滢，武全胜，朱一峰

(1. 朝阳师范高等专科学校 数学计算机系，辽宁 朝阳 122000；2. 朝阳师范高等专科学校 教务处，辽宁 朝阳 122000)

一类二阶中立型Emden-Fowler方程的振动条件

于海芳1，韩 滢1，武全胜1，朱一峰2

(1. 朝阳师范高等专科学校 数学计算机系，辽宁 朝阳 122000；2. 朝阳师范高等专科学校 教务处，辽宁 朝阳 122000)

考虑带有两个参数α和β的二阶中立型Emden-Fowler方程 (r(t)|z′(t)|α-1z′(t))′+q(t)|x[σ(t)]|β-1x[σ(t)]=0 ，利用广义Riccati变换、积分不等式等方法给出了两个新的振动结论，所得条件推广了文献中的结论.给出两个例子进一步证明振动条件的正确性.

振动；中立型；时滞；Emden-Fowler方程

本文考虑二阶中立型Emden-Fowler方程：

(r(t)|z′(t)|α-1z′(t))′+q(t)|x[σ(t)]|β-1x[σ(t)]=0,t≥t0,

(E)

其中z(t)=x(t)+p(t)x[τ(t)],r(t)∈C1([t0,∞),R),p(t),q(t)∈C([t0,∞),R)，α和β是两个常数,且满足下列条件：

A1:α>0,β>0,

A2：0≤p(t)≤1,q(t)≥0,r(t)>0,r′(t)≥0

近年来，随着数值计算，生物数学，计算机科学，自动控制技术的发展，用时滞微分方程描述的模型越来越多，Emden-Fowler方程的理论越来越完善.而对于Emden-Fowler方程解的振动性研究早在20个世纪60年代就已经开始.1963年I·T·Kiguradze[1]考虑普通的Emden-Fowler

u″=a(t)un=0 ，

(E1)

与此同时给出了该方程的几个经典的振动结论.

1975年，Wong[2]对方程(E1)进行改进，对方程(E2)进行了研究，同时给出了此振动的一系列条件.

x″(t)+q(t)|x(t)|α-1x(t)=0,t≥t0,

(E2)

之后，人们对方程(E2)又做了进一步的改进，加入了时滞项，并且二次导数项的系数也由一变为不定的，即

(r(t)|x′(t)|α-1x′(t))′+q(t)|x[σ(t)]|α-1x[σ(t)]=0,t≥t0.

(E3)

对于方程，Dzurina、Sun等学者都证明了它的一系列振动结论[3-8].

2012年，Liu等[9]人再次改进方程，讨论广义Emden-Fowler方程(E)，并且给出了当α>β>0时方程振动的条件.

定义1：方程的解为最终正解(或最终负解)是指，如果存在常数t0>0，使当t≥t0时，方程的解x(t)>0(或x(t)<0).

定义2：若方程的有界解既不是最终正解也不是最终负解，则称方程的有界解是振动的，否则方程的有界解是非振动的.

定义3：方程的解x(t)是振动的，如果它有任意大的零点，否则称为非振动的.若方程所有的解都是振动的，则称该方程是振动的.

1 主要结果

定理1：假设A1-A4均成立，且α>1，β>1，若存在ρ(t)∈C1([t0,∞),(0,∞))，使

则方程(E)振动.其中Q(t)=q(t)(1-p[σ(t)])β.

证明：假设方程E有非振动解x(t).不失一般性，我们可设x(t)>0(x(t)<0的证明方法与x(t)>0的相似)，则存在t2≥t1，使得τ(t2)≥t1,σ(t2)≥t1所以x[σ(t)]>0，x[τ(t)]>0，z(t)=x(t)+p(t)(x[τ(t)])>0,t≥t1≥t0.

由方程(E)知：(r(t)|z′(t)|α-1z′(t))′=-q(t)|x[σ(t)]|β-1x[σ(t)]<0，

(1)

则r(t)|z′(t)|α-1z′(t)是单调递减函数，所以z′(t)定号，即z′(t)>0或z′(t)<0.

我们断言z′(t)<0不存在，这是因为假设z′(t)<0，则

(r(t)(-z′(t))α-1z′(t))′<0 ，

(-r(t)(-z(t))α)′<0即，所以-r(t)(-z′(t))α是单调递减函数，由此可以推出当t≥T时，我们有-r(t)(-z′(t))α≤-r(T)(-z′(T))α=-k,k>0，

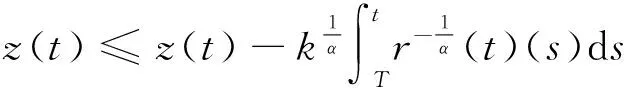
当t→∞时，由A4知z(t)<0，这与z(t)>0矛盾，所以z′(t)>0.

接下来讨论α与β的关系(任意的ρ(t)∈C1([t0,∞),(0,∞)))：

(2)

1)当α>β时

由z(t)=x(t)+p(t)(x[τ(t)]) ，得x(t)=z(t)-p(x)(x[τ(t)]).又因为x[τ(t)]≤z[τ(t)]≤z(t)，所以x(t)≥z(t)-p(t)z(t)=z(t)(1-p(t)) ，

即

(x[σ(t)])β≥(z[σ(t)])β(1-ρ[σ(t)])β.

由(r(t)(z′(t))α)′+q(t)(x[σ(t)])β=0可得

(r(t)(z′(t))α)′+q(t)(1-p[σ(t)])β(z[σ(t)])β=(r(t)(z′(t))α)′+Q(t)(z[σ(t)])β≤0，

即

(3)

由w(t)的定义知

(4)

因为(r(t)(z′(t))α)′=r′(t)(z′(t))α+αr(t)(z′(t))α-1z″(t)≤0，所以z″(t)≤0,即z′(t)是单调递减函数，由此可推出

z′[σ(t)]≥z′(t) .

(5)

对w(t)求导，并结合式(3)～(5)式得：

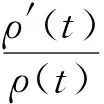
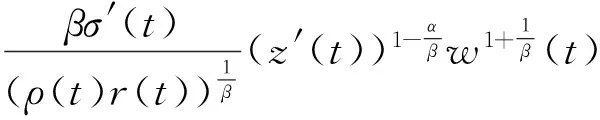
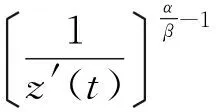
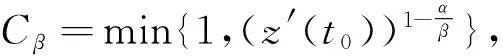
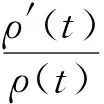
(6)

2)当β≥α时

因为r(t)(z′(t))α是单调递减函数，所以r(t)(z′(t))α≤r[σ(t)](z′[σ(t)])α.

由此可得

(7)

由w(t)的定义知

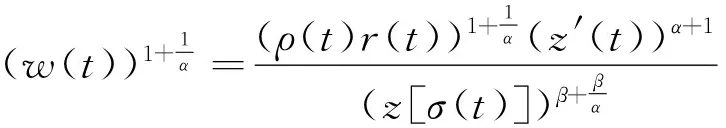
(8)

对w(t)求导，并结合式(3)、(7)、(8)得：

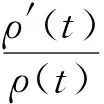
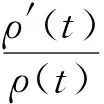
(9)

因为z′(t)>0，所以z(t)是单调递增函数，即对任意的t≥t0，有z(t)≥z(t0).

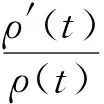
(10)

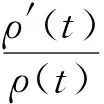
(11)

即对任意的ρ(t)∈C1([t0,∞),(0,∞))，式(11)均成立，所以

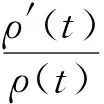
(12)

其中b是常数.

对不等式两边在[T,t]上同时积分得

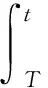
(13)

(14)

定理2：假设A1-A4均成立，且β>α>0，若

证明：假设方程(E)有非振动解x(t).不失一般性，我们可设x(t)>0(x(t)<0的证明方法与x(t)>0的相似).

取ρ(t)=1，则由式(9)得w′(t)≤-Q(t)，对不等式两边同时积分得

(15)

(16)

所以

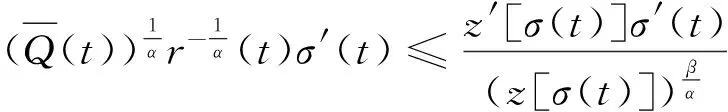
(17)

对不等式两边从[T,t]同时积分得

(18)

2 算 例

例1：考虑下面的方程

(19)

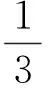
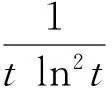
由定理1知方程(19)是振动的.

例2：考虑下面的方程：

(20)

由定理2知，方程(20)振动.

3 结 语

本文考虑的是一类广义二阶中立型Emden-Fowler方程解的振动性问题，利用广义Riccati变换、积分不等式以及一些常用的不等式等方法得到了方程的两个新的振动结论.其中定理1是对文献[9]的一个推广，即在不限制和的大小的情况下得到的振动条件.定理1.2是在当时方程解振动的结论.文章的最后给出两个例子说明振动条件的正确性.

[1] KIGURADZE I T. On the asymptotic properties of solutions of the equation[J]. Sobbsc. Akad. Nauk. Gruzin SSR, 1963(30): 129-136.

[2] WONG J S W. On the generalized Emden-Fowler equation [J]. SIAM Rev, 197(17): 339-360.

[3] DZURINA J, STAVROULAKIS I P. Oscillation criteria for second-order delay differential equations [J]. Appl. Math.Comput, 2003, 140(2-3): 445-453.

[4] SUN Y G, MENG F W. Note on the paper of Dzurina and Stavroulakis [J]. App.Math.Comput, 2006, 174(2): 1634-1641.

[5] LI H J, YEH C C. Nonoscillation criteria for second-order half-linear differential equations [J]. Appl. Math. Lett, 1995, 46(3): 194-215.

[6] HSU H B, YEH C C. Oscillation theorems for second-order half-linear differential equations [J]. Journal of Mathematical Analysis & Applications, 2005, 9(4): 845-861.

[7] WANG Q R. Oscillation and asymptotics for second-order half-linear differential equations [J]. App. Math. Comput, 2004, 48(1): 61-72.

[8] AGARWAL R P. Oscillation criteria for second-Order retarded differential equations [J]. Mathl. Comput. Modelling, 1997, 26(4): 1-11.

[9] LIU H D, MENG F W, LIU P C. Oscillation and asymptotic analysis on a new generalized Emden-Fowler equation [J]. Appl. Math. Comput, 2012, 219(5): 2739-2748.

Oscillationcriteriaforaclassofsecond-orderneutralEmden-Fowlerequations

YU Hai-fang1, HAN Ying1, WU Quan-sheng1, ZHU Yi-feng2

(1. Department of Mathematics and Computer Science, Chaoyang Normal College, Chaoyang 122000, China; 2. Academic Affairs Office, Chaoyang Normal College, Chaoyang 122000, China)

In this paper, the second-order neutral Emden-Fowler equations with two parametersαandβ(r(t)|z′(t)|α-1z′(t))′+q(t)|x[σ(t)]|β-1x[σ(t)]=0 was considered.This paper used the generalized Riccati transformation technique and integral inequality to establish two new oscillation criteria. Some well-known results in the literature were extended. At the end of the paper, two examples will be given to show the sharpness of our results.

oscillation; neutral; delay; Emden-Fowler equations

2016-12-13

辽西北职业教育联盟2016年职业教育集团化办学专项研究课题(LM201620)；朝阳师范高等专科学校职业教育研究专项课题(ZJZX1713).

于海芳(1980-)，女，硕士，讲师，研究方向：应用数学.

O175

A

1672-0946(2017)05-0621-05