基于TDOA定位的阵列布放结构研究

金博楠，徐晓苏，张 涛，李 瑶

(东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室，南京 210096)

基于TDOA定位的阵列布放结构研究

金博楠，徐晓苏，张 涛，李 瑶

(东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室，南京 210096)

不同结构阵列在TDOA定位中对定位精度有较大影响。为了掌握和减小阵列带来的影响，从TDOA定位解算方程组的角度分析了平面阵列在空间定位中高度方向产生较大误差的原因；又从单个基线的角度分析了影响基线定位敏感度的因素，而为分析阵列定位效果提供了理论依据。然后对七种代表性的平面阵列进行对比，验证了阵列结构对定位精度的影响关系。根据平面阵列的经验又设计了三种空间阵列，通过仿真实验证明了对阵列结构研究的正确性。

TDOA; 阵列结构;传感器布放;长基线定位

E-mail:jinbonan@seu.edu.cn

0 引言

基于到达时间差(Time Difference of Arrival，TDOA)的长基线定位技术作为水下声学定位中的重要研究方向，受到了越来越多的关注。由于接收端不需要与发射端进行时钟同步[1]，在接收端完全可以被动地探测和定位正在发射信号的目标，因此在反潜、追踪、勘探、搜救等领域有着广泛的应用[2-4]。影响TDOA定位精度的因素主要分为前端接收和后端解算两个部分，前端误差指水听器接收信号并分析时间差过程中产生的误差，主要包括噪声干扰、多途效应、信号衰减等带来的观测误差以及声速变化，时延提取过程中的计算误差；后端误差主要包括选用算法的估计误差、阵列布放结构和安装误差未补偿等造成的误差。长基线定位发展至今，基于TDOA的定位算法层出不穷，涌现出包括SI、SX、Chan、Taylor等许多经典算法，还有神经网络、蚁群算法、二阶锥规划以及基于概率论的滤波算法[5]。关于水听器阵列布放规则对定位精度的影响的研究并不深入，文献[6-7]研究针对平均圆周分布的中心平面阵进行了对比，这种阵列有一定的局限性。本文主要针对阵列的布放阵型的布放准则，从单个基线的角度进行了研究，并基于此在二维平面下对多个代表性的阵列结构进行了对比仿真。分析了三维方向上的灵敏度问题，对空间定位中的三维阵列布放问题进行了研究设计，并对通用阵型的布放准则提出一些建议。

1 灵敏度分析

1.1 高度方向灵敏度

很多算法将三维问题简化至二维平面进行分析，虽然这种过渡理论上没有问题，但实际应用上由于条件限制，空间定位往往还是以平面阵列居多，这就带来了高度方向上的误差。

设待测目标MS的坐标为zp=[x,y,z]T，第i个基元BS的坐标为si=[xi,yi,zi]T，i=0,1,2,3，…，N，其中0号BS为参考，MS与BS之间的距离关系为

i=0,1,2,3，…，N

(1)

取BS0为公共参考基元，得到一组TDOA观测量τi,1(i=0,1,2,3，…，N)，分别表示BSi和BS0之间的信号到达时间差

ri0=cτi0=ri-r0，i=1,2,3，…，N

(2)

式(2)展开是一个双曲线方程，假设为视距环境下，且声波传播速度不变为c，则可建立N个关于zp的双曲面方程。求解该方程组即可得到MS的坐标。因此，如图1所示，二维TDOA定位从几何上可归结为双曲线定位，在三维空间就是双曲面定位。在没有误差的理想情况下，3个方程就可以求解3个未知数，即3个曲面的交点就是MS的位置。然而因为时间差存在误差且可能较大，使得3个曲面不交于一点，曲面的多个交叉处又可能出现模糊解，所以往往需要5个以上的BS建立多于3个的方程来寻求最优解。

图1 TDOA定位原理示意图Fig.1 The scheme of TDOA localization

i=0,1,2,3，…，N

(3)

当i=0时，ri0=0，因此

(4)

用式(3)减去式(4)可得

i=1,2,3，…，N

(5)

考虑到实际中的噪声，稍加整理，可得

i=1,2,3,…,N

(6)

将式(6)写成矩阵形式

(7)

对式(7)的方程组求解，即可得出MS的坐标[8]。

1.2 基线方向灵敏度

下面从另一个角度建模分析。MS、BS0和任意一个BS可组成一个三角形，如图2所示，zp为MS位置，s0为BS0位置(设为原点)，si为BSi位置，r0为中心斜距，ri为MS和BSi的斜距，di为基线长度(假设和X轴重合)。

图2 单个基线与MS的三角关系Fig.2 The triangular relationship between single baseline and MS

根据余弦定理可知

(8)

将式(2)代入式(8)，整理可得

(9)

其中,x=r0cosα，为基线方向的投影。

根据式(9)可以得到ri0在3个方向上的偏导数，即灵敏度：

(9)

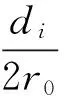
(10)

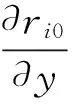
对于空间中任意方向的基线，对应坐标轴方向上的灵敏度为：

(11)

其中，A、B、C分别是基线与坐标轴夹角，则dicosA、dicosB、dicosC为基线在各坐标轴上的投影分量。α、β、γ分别是中心斜距与坐标轴夹角。

此外，基线方向的灵敏度和基线长度、距离差成正相关，和斜距成负相关。因此往往MS在阵列内部时，定位精度比远离阵列时的定位精度高。

1.3 阵型类型

结合上面的计算分析，就可以对空间中可能出现的几种阵列布放(或者近似型)做出一定的判断。

1.3.1 直线阵

所有基元集中在一条直线上，即基线方向重合(假设为x方向)，阵列为直线型，这种摆放在一个方向上(x方向)有很高的精度，而在另外2个方向(y,z方向)上的精度则表现很差。如图3(a)所示。

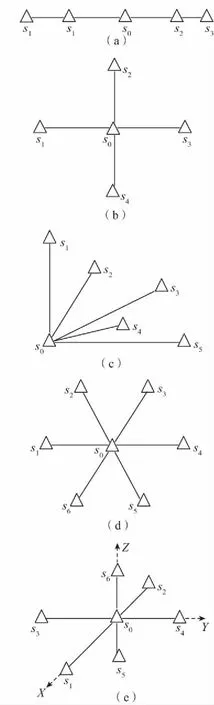
图3 不同阵列示意图Fig.3 The scheme of different sensor array placements

1.3.2 平面阵

所有基元都集中在一个平面上，即基线都在同一平面内。三维空间定位中，若高度方向没有基线，则在高度方向的定位精度将较差。平面阵具体又可分为中心阵和扇形阵。

中心阵正中放置参考基元，其他基元分布四周，如十字阵(图3(b))、六角阵(图3(d))、星型阵等。

扇形阵参考基元放在一侧，其他基元分布于另一侧，如L阵、爪字阵、兀字阵等(图3(c))。

1.3.3 空间阵

种类和平面阵类似，在x、y、z3个方向上均有基线或明显的基线分量，这种阵型能够对3个方向的精度提供保障。个别基线集中的布放可视为极端情形为直线阵，平面阵进行分析，如图3(e)所示。

2 仿真对比

通过计算机仿真出平面下不同阵型对相同目标的定位误差。结合之前的理论推导，对不同阵型的效果进行对比分析。之后根据平面条件下多种阵型的定位效果设计空间中的三维阵列结构并仿真验证其设计的可行性。采用Chan估算初值并用Taylor算法修正的定位算法来得到MS位置估计[9]。

2.1 平面实验

对平面直角坐标系下x∈[-500,500]，y∈[-500,500]的方形区域布放阵列，在x=200,y∈[-600,600]的线段上均匀地选取13个点作为MS的位置。距离差观测量上叠加均值为1.5的白噪声。每个位置以5000次的蒙特卡罗试验的定位误差均值作为最终结果。本次仿真设计了7种阵型[10]，具体如表1所示。

表1 平面阵型参数

实验结果如图4、图5所示，图4是估计位置和真实位置的距离误差曲线；图5是在X方向和Y方向的误差分量，图中横坐标是各个MS的纵向距离。

由图4可知，直线阵列的定位误差较大，尤其当MS在远离阵列时Y方向阵列发散明显，而阵列中心位置时X方向阵列也会发散。两端发散的现象在各阵列中都存在，只不过爪字型阵列的抑制效果稍好。无论是长基线定位还是短基线定位，工作范围都是有限的，一般与基线长度相当，对基阵外较远距离的目标定位时，定位结果就不是那么精确了。这一实际情况与本文上面提到的定位误差两端发散现象是一致的，就阵列内部的定位效果看，L字阵列定位误差存在不对称的大幅增长，十字阵列效果一般，非垂直阵列和爪字阵列精度较高。下面具体从X和Y2个方向的误差来分析导致上述区别的原因。

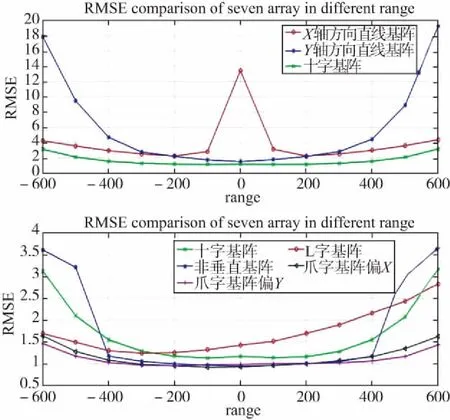
图4 七种阵型定位误差对比图Fig.4 The error comparison of seven placements

图5 七种阵型定位误差：(a)X方向对比图;(b)Y方向对比图Fig.5 The error comparison of seven placements： (a) in X direction; (b) in Y direction

2个不同指向布放的直线阵列，很显然X向阵列在X方向表现很好，它的误差主要来自Y方向定位能力不足，当MS靠近基线时，计算过程容易出现奇异导致Y方向定位发散；相反，Y向阵列在X方向定位能力不足，Y方向两端发散是因为SM处于基线范围以外，由式(9)可知，大部分基线的灵敏度都变得很低，因此误差变大。见图5(a)上和(b)上。

2个爪字阵列的区别在于第4条基线分别靠近2个轴，因此在轴向的基线分量彼此各有优势。图5(a)中和(b)中如实地反映出这一现象，偏X轴的爪字阵列在X方向精度更高，而偏Y轴的爪字阵列则在Y方向精度更高。此外，MS大部分位置对于爪字阵列的每一条基线来说都属于内部，即使两端边缘位置也不会超出基线太远，因此爪字阵列两端发散现象抑制得较好。基于式(9)所体现的设计原则，在所有七种阵列中，爪字阵列也是效果最好的。

与爪字阵列类似的L字阵列则没有那么好的效果，相比之下主要原因是2条较短的基线没有充分发挥基线补充的作用，当MS在靠近(200,600)时，基线灵敏度降低效益凸显，所以定位误差呈不对称增长且主要发生在X方向。见图5(a)下和(b)下。

同理，对于十字阵列来讲，MS在大部分位置都会处于2条基线外，且其4条基线长度都较短，因此灵敏度不会很高，两端发散的现象和爪字阵列比还是较明显的。见图5(a)下和(b)下。

设计非垂直阵列是为了观察基线垂直与否对定位效果的影响。从图5(a)下和(b)下来看，并没有太大影响，MS在基线内部时的定位精度反而非常好。将非垂直阵列的4条基线投影到轴线方向，Y方向的基线分量很小，因此非垂直阵列在Y方向上出现了两端发散的现象。

2.2 空间实验

在三维情况下，根据平面实验结果，在阵型选取时应当避开某一方向基线分量不足的情形，本文设计了三种阵型进行比较，分别是：顶角辐射阵列、中心辐射阵列和面心辐射阵列，如图6所示。定位误差对比结果如图7所示。

图6 顶角辐射阵列(○)，中心辐射阵列(*)和面心辐射阵列(△)Fig.6 Corner radiation array(○);center radiation array(*);centroid radiation array(△)

实验结果表明，三种阵列都能提供较高的定位精度。从选取的MS测试位置的定位效果来看，同样是8条基线，中心辐射阵列要比面心辐射阵列效果略好。顶角辐射阵列在只有7条基线的情况下表现出和中心辐射阵列同样的效果，表明顶角辐射阵列具有较好的定位效果，基线数量不是决定定位精度的唯一因素，合理的阵型布放能够有效改善定位精度。根据上述三种阵列的对比，在待测区域一定、基线数目一定的条件下，顶角辐射阵列可以作为优先选择。

图7 (a)距离误差;(b)X方向误差;(c)Y方向误差;(d)Z方向误差Fig.7 (a) The error in distance; (b) The error in X direction; (c) The error in Y direction; (d) The error in Z direction

3 结论

由理论推导和平面仿真可知，某一方向若没有基线分量或分量很小时，定位结果在该方向上容易发散。因此空间定位时，在高度方向上不能布放基元的情况下，由于条件限制，外部高度信息辅助显得十分必要。基线方向的敏感度直接影响着该方向的定位精度、敏感度与基线长度、距离差成正相关，和参考基元外的基元斜距成反比。尽可能增大基线长度，避免距离基元过远的位置情况出现，这样能充分发挥阵列定位性能。增加基线数目可以提高定位精度，但合适的基线结构不仅能节约成本，还能进一步提高定位效果。

文献[6-7，10]主要对几种平均圆周分布的中心平面阵进行了研究比较，阵列的基本组成结构始终没有太大改变。本文从基线角度出发，在几何理论上推导了阵列的影响因素，从本质上分析研究影响阵列差异的原因，从而能够对平面乃至空间上所有可能存在的阵列布放形式作出判断，并对多种代表性的阵列进行了仿真验证。

有些阵型对于某些位置具有较高的局部精度，不能就此判断好坏。MS在不同位置，定位精度各不相同，实验中只是选取了一些具有代表性的位置，通过多个位置的平均表现初步认为文中的爪字阵列和顶角辐射阵列较为优秀。然而阵列的结构不胜枚举，没法得到最优阵列的结论，只能通过上述准则和使用需要去设计更好更合适的阵列。在今后的研究中将对各个阵列整个测量区域的精度分布进行分析，并采取一定措施进一步提高阵列的定位效果。

[1] Xu B, Sun G, Yu R, et al. High-accuracy TDOA-based localization without time synchronization[J]. IEEE Transactions on Parallel and Distributed Systems,2013, 24(8): 1567-1576.

[2] Yu X, Wu C, Cheng L. Indoor localization algorithm for TDOA measurement in NLOS environments[J]. IEICE Transactions Fundamentals, 2014, 97(5): 1149-1152.

[3] Nosal E M. Methods for tracking multiple marine mammals with wide-baseline passive acoustic arrays[J]. The Journal of the Acoustical Society of America, 2013, 134(3): 2383-2392.

[4] Zhang T, Chen L, Li Y. AUV underwater positioning algorithm based on interactive assistance of SINS and LBL[J]. Sensors, 2016, 16(1):42.

[5] Li X, Deng Z D, Rauchenstein L T, et al. Contributed Review: Source-localization algorithms and applications using time of arrival and time difference of arrival measurements[J]. Review of Scientific Instruments, 2016, 87(4):041502.

[6] Meng W, Xie L, Xiao W. Optimal TDOA sensor-pair placement with uncertainty in source location[J]. IEEE Transactions on Vehicular Technology, 2016,65(11): 9260-9271

[7] Kim S H, Park J H, Yoon W, et al. A note on sensor arrangement for long-distance target localization[J]. Signal Processing, 2017, 133: 18-31.

[8] Xu B,Qi W D,Wei L, et al. Turbo-TSWLS: enhanced two-step weighted least squares estimator for TDOA-based localization[J]. Electronics Letters, 2012, 48(25): 1597-1598.

[9] Chen D, Tang H, Wu J. Research of TDOA cooperative location algorithm based on Chan and Taylor[J].Computer Scienc, 2011, 38(10):406-411.

[10] Lui K W K, So H C. A study of two-dimensional sensor placement using time-difference-of-arrival measurements[J]. Digital Signal Processing, 2009, 19(4): 650-659.

StudyofArrayStructureforSensorPlacementinTDOA-BasedLocalization

JIN Bo-nan, XU Xiao-su, ZHANG Tao, LI Yao

(Key Laboratory of Micro-Inertial Instrument and Advanced Navigation Technology of Ministry of Education, School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China)

Different sensor placements have a great influence on the accuracy in TDOA-based localization. In order to grasp and decrease the influence brought by the array, the causes of the large errors in the vertical direction are analyzed with TDOA localization equations when the planar array is used in the spatial orientation. Then, the factors affecting the localization sensitivity of the baseline are deduced from the perspective of a single baseline, which provides the theoretical basis for analyzing the positioning accuracy of the sensor arrays. Then the positioning errors of seven representative planar arrays are compared to verify the relationship between the array structure and the positioning accuracy. According to the application experience of planar array, three kinds of spatial sensor array placements are designed. The simulation results demonstrated the correctness of the study on array structure.

TDOA; Array structure; Sensor placements; Long baseline localization

10.19306/j.cnki.2095-8110.2017.06.005

TN961

A

2095-8110(2017)06-0029-08

2017-03-14；

2017-03-28

国家自然科学基金(61473085，51175082，51375088，61273056)

金博楠(1990-)，男，博士研究生，主要从事声学定位和组合导航方面的研究。