基于简化Mohr模型的光纤陀螺温度补偿方法研究

那永林

(北京自动化控制设备研究所，北京 100074)

基于简化Mohr模型的光纤陀螺温度补偿方法研究

那永林

(北京自动化控制设备研究所，北京 100074)

为了提高光纤陀螺温度补偿精度，采用Mohr理论建立了光纤环圈的热传递模型，准确分析了光纤环圈内部的温度变化和分布情况，计算得到了光纤环圈的Shupe误差。根据Shupe理论误差和陀螺仪输出的相关性分析，得到了最优的光纤环圈热传递参数。根据热传递参数建立了光纤陀螺温度补偿模型，完成了光纤陀螺的实时温度补偿，实际补偿后光纤陀螺仪变温精度提高了约3.4倍。

光纤陀螺；温度补偿；Mohr模型

0 引言

光纤陀螺是一种基于Sagnac效应的角速率传感器，具有动态范围大、可靠性高、启动时间短，体积小、成本低等优点，广泛应用于武器系统、潜艇舰船、飞机导航、卫星定位等领域。高精度光纤陀螺易受各种环境条件的影响，其工程应用的精度往往低于其理论精度。温度变化条件下的精度是光纤陀螺工程应用的一个重要指标，也是光纤陀螺工程化过程中的一个技术难点。

提高光纤陀螺的变温精度主要方法是降低光纤陀螺自身的温度敏感度，对光纤陀螺进行温度控制或温度补偿。其中温度补偿技术是导航级(0.1(°)/h～0.01(°)/h)光纤陀螺普遍采用的技术途径之一。通常温度补偿多采用多项式补偿方法，多项式补偿方法存在较大的残余误差，不能满足高精度光纤陀螺的使用需求。

本文提出了一种基于简化Mohr模型的光纤陀螺温度补偿参数确定方法，首先建立了光纤环圈Mohr理论模型，得到光纤环圈内部的温度分布和温度变化规律，进而计算出光纤陀螺在温变条件下的Shupe误差。根据Shupe理论误差和陀螺仪输出的相关性分析，得到了最优的光纤环圈热传递参数，实现了高精度的温度补偿。

1 光纤陀螺的Shupe效应

Shupe效应误差是干涉式光纤陀螺存在的主要误差源之一，在环圈内部顺、逆时针方向传播的两束光受到时变温度梯度的影响，经历了不同的光程，从而产生了寄生相位差，称之为Shupe效应误差。Shupe效应误差可以表示为

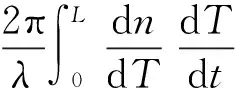
(1)

Shupe误差的典型输出曲线如图1所示。图中红色曲线是陀螺仪内部温度变化情况，温度变化速率为0.5℃/min，温度变化范围-40℃～+60℃。黑色曲线是变温情况下陀螺仪的零位输出。从图1中可以看出，当温度发生变化时，陀螺仪的零位会随着温度的变化而产生漂移，这种漂移引入的零位误差就是Shupe误差。

图1 Shupe效应误差和温度变化关系图Fig.1 The shupe error and the temperature in the FOG

通过在陀螺仪内部放置温度传感器，可以实时监测陀螺内部温度变化，进而实现Shupe误差补偿。图2所示为根据Shupe误差理论，对图1的陀螺仪零位输出曲线进行温度补偿，补偿前的陀螺仪零偏稳定性为0.174(°)/h，补偿后的零偏稳定性为0.0134(°)/h。补偿后陀螺精度提高了1个数量级，但从图2中可以看出，补偿后还存在较大的零位残差。

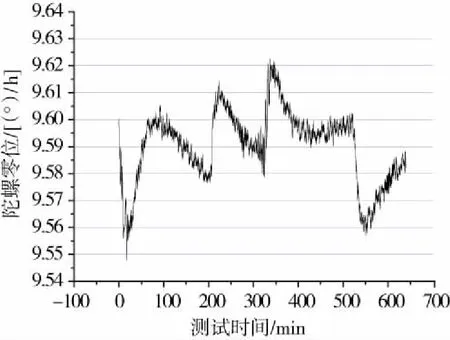
图2 Shupe效应误差温度补偿结果Fig.2 The compensation of the Shupe error

由于Shupe误差是环圈内部温度变化引起的，受到光纤环圈制作工艺以及温度传感器的尺寸所限，不可能将温度传感器放置到环圈的内部，只能采用一个光纤传感环圈外部的温度传感器，这个传感器所采集的温度不能真正反应环圈内部温度，因此无法真实准确地监测环圈内部温度，而采用这个温度数据对陀螺仪零位变化进行温度补偿，两者之间存在的温度差异是补偿残差存在的主要原因。

2 光纤传感环圈的Mohr模型

Mohr用电路传输线中的电流流动模拟光纤环圈内的热传递过程，采用电容模拟环圈内部的比热容，采用电阻模拟热导率。Mohr模型能够很好地反应环圈内部热传递过程。本文主要研究了基于轴向传热的无骨架光纤环圈。图3所示为某光纤传感环圈内部热传递过程的示意图，在陀螺仪内部光纤环圈和外界的热交换主要包括环圈底面的热传导以及其他几个表面的热辐射过程。对于有骨架的光纤环圈，只需要修改其中的几个热传递参数，传热模型依然适用。

图3 无骨架光纤环圈热传递示意图Fig.3 The thermal transfer model of fiber loop

图3中光纤环圈由m层n匝光纤组成，根据图中的传热路径建立一个基于热容和热阻参数的简化Mohr模型，如图4所示。

图4 光纤传感环圈简化热传递Mohr模型Fig.4 Simplified Mohr model of fiber loop

采用计算机仿真分析方法，根据图4的模型，可以计算出光纤环圈内部第i层第j匝光纤在t时刻的温度T(i,j,t)。T(i,j,t)是由外界的温度变化以及环圈内部的热容、热阻等参数共同决定的。

为了得到温度变化引起的Shupe误差，还必须确定第i层第j匝光纤沿光传播方向的坐标值。以四级对称缠绕为例，图5给出了四级对称缠绕的光纤排列示意图。

图5 四级对称缠绕光纤排列示意图Fig.5 The model of quadrupe-winding

根据四级缠绕光纤的排列关系，可以得到第i层第j匝光纤的位置坐标z(i,j)

将T(i,j,t)和z(i,j)代入式(1)中，可以仿真得到环境温度变化引起的光纤陀螺Shupe误差，如图6所示。图中黑色曲线是光纤陀螺的实际输出曲线，而红色曲线是采用Mohr模型仿真得到的Shupe误差曲线。

图6 Mohr模型仿真曲线和实际输出对比图Fig.6 The simulation graph of Mohr model and output of FOG

从图6中可以看出，理论计算得到的Shupe误差和陀螺仪实际零位具有很高的相似度，能够很好地反应陀螺仪的零位变化，因此可以根据Mohr模型的计算结果实现光纤陀螺零位的温度补偿。

3 基于Mohr模型的温度补偿方法

采用Mohr模型对光纤陀螺进行温度补偿，必须根据光纤传感环圈材料的热容、热组参数序列{r,c,R1,C1,R2,C2,…,Rn,Cn}，计算出光纤环圈内部各个时刻的温度分布情况，再根据Shupe误差公式计算出光纤陀螺仪零位的变温漂移，从而实现温度补偿。图7所示为采用普通方法进行温度补偿和采用Mohr模型进行温度补偿的补偿结果对比，采用Mohr模型补偿后精度由采用普通方法的0.0134(°)/h提高到0.0088(°)/h，提高了约35%。

图7 采用Mohr模型温度补偿对比图Fig.7 The comparison of compensation with Mohr model

从图7中可以看出，采用Mohr模型进行温度补偿后补偿结果仍然存在较大的残差。这是由于实际的热容、热阻参数序列{r,c,R1,C1,R2,C2,…,Rn,Cn}会受到生产工艺的影响，和理论结果存在较大的差异，对补偿结果产生影响，不能达到最优的补偿结果。

4 Mohr模型最优参数拟合

为了进一步提高温度补偿精度，本文采用Pearson相关系数(式(3))方法来寻找最优补偿参数。

(3)

通过计算Mohr模型和陀螺输出的Pearson线性相关系数，可以得到采用不同的热容、热阻参数序列的相关性曲线，如图8所示。

图8 不同参数序列对应的相关系数Fig.8 The correlation graph of parameters

可以看出相关系数具有单调特性，相关系数的极值位置对应的参数序列就是这只陀螺仪温度补偿的最优温度参数。采用此参数对陀螺仪进行温度建模和补偿可以得到最优效果。最优参数序列得到的Mohr模型和陀螺仪输出的对比曲线如图9所示。图10给出了采用最优参数序列进行温度补偿的补偿结果曲线。

图9 Mohr模型曲线和陀螺输出曲线Fig.9 The output curve of Mohr and FOG

图10 温度补偿结果图Fig.10 The graph of compensation result based on Mohr model

采用最优参数序列，对陀螺仪进行温度补偿，补偿后精度由补偿前的零偏稳定性0.174(°)/h提高到0.0035(°)/h。

这种方法不需要精确测定环圈的热容、热阻等温度参数，而是通过试验的方法得到一个综合的温度参数序列，根据陀螺仪的温度变化规律得到仿真的输出曲线，计算仿真输出和实际输出相关系数，由相关系数极值确定最优的温度参数序列。这个参数序列保证了陀螺补偿效果最优。

5 试验结论

根据这个补偿算法，本文对9只陀螺进行了温度补偿，补偿结果如表1所示，采用基于简化的Mohr模型温度补偿方法，可以将光纤陀螺仪的精度提高约3.4倍左右。

表1光纤陀螺实际补偿效果统计表

Tab.1ThecompensationeffectsstatisticaltableofFOG

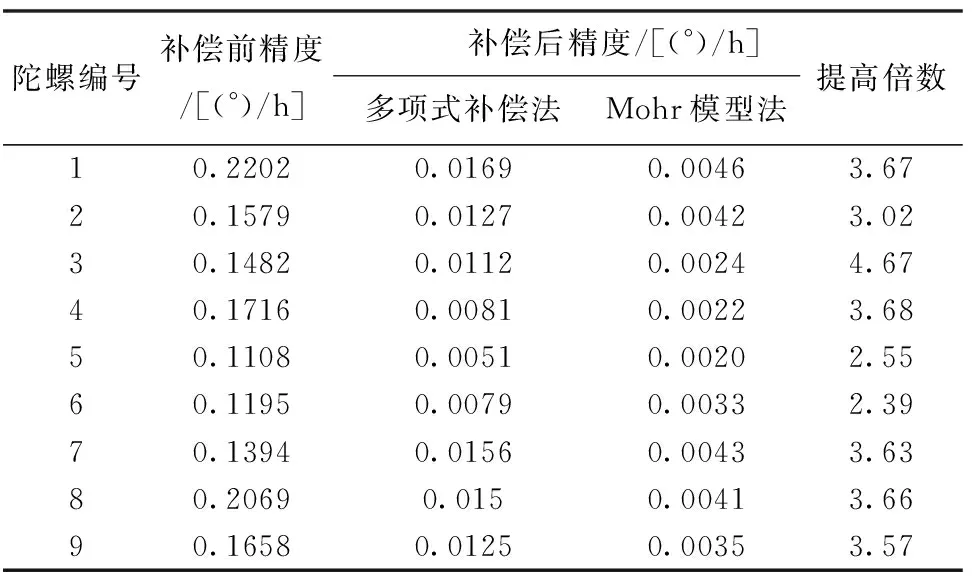
陀螺编号补偿前精度/[(°)/h]补偿后精度/[(°)/h]多项式补偿法Mohr模型法提高倍数10.22020.01690.00463.6720.15790.01270.00423.0230.14820.01120.00244.6740.17160.00810.00223.6850.11080.00510.00202.5560.11950.00790.00332.3970.13940.01560.00433.6380.20690.0150.00413.6690.16580.01250.00353.57

6 结论

本文采用简化的Mohr模型，估算了光纤陀螺传感环圈内部的温度变化趋势，实现了光纤陀螺温度Shupe误差补偿，补偿后光纤陀螺仪的精度和传统补偿方法相比提高了3.4倍左右。采用这种方法，只需要在光纤陀螺仪内部放置一个温度传感器，补偿算法复杂度低、可靠性高，工程实用性强。

[1] 张桂才,王巍.光纤陀螺仪[M]. 北京: 国防工业出版社,2002.

[2] Shupe D M. Thermally induced nonreciprocity in the fiber-optic interferometer[J]. Applied Optics, 1980, 19(5): 654-655.

[3] Lefère H C. Fundamentals of the interferometric fiber-optic gyroscope[J]. Optical Review, 1997, 4(1): 20-27.

[4] 张桂才,王巍.光纤陀螺敏感线圈的温度漂移特性与绕圈技术研究[J].中国惯性技术学报, 1998,6(1):41-45.

[5] Mohr F. Thermooptically induced bias drift in fiber optical Sagnac interferometers[J]. Journal of Lightwave Technology, 1996, 14(1): 27-41.

[6] 冯文帅,王学锋,王巍.光纤环的每层匝数不同对光纤陀螺温度性能影响[J]. 中国惯性技术学报,2011,19(4):487-493.

TemperatureCompensationResearchforFOGBasedonMohrModel

NA Yong-lin

(Beijing Institute of Automatic Control Equipment, Beijing 100074,China)

To improve compensation precision of FOG, thermal transfer model of fiber loop based on Mohr theory was established. The temperature changing and thermal distribution of fiber loop was analyzed, and Shupe error of fiber loop was computed. The correlation of the output of FOG and Shupe error is simulated. The optimum thermal transfer parameters of fiber loop was attained.The Shupe error compensation models are established. The real-time compensation of FOG error is designed to verify the effect, the bias stability is 50 times higher than the original one.

Fiber optic gyro; Temperature compensation; Mohr model

10.19306/j.cnki.2095-8110.2017.06.016

V241.5

A

2095-8110(2017)06-0098-04

*

2017-09-30；

2017-10-31

装备发展部预先研究项目

那永林(1976-)，男，博士，研究员，主要从事光纤陀螺技术研究。Email：16289351@qq.com