结合总变差和组稀疏性的压缩感知重构方法

朱 俊, 陈长伟

(1.金陵科技学院 计算机工程学院， 南京 211169； 2.南京晓庄学院 信息工程学院， 南京 2111711；3.江苏省社会安全图像与视频理解重点实验室(南京理工大学)， 南京 210094)

结合总变差和组稀疏性的压缩感知重构方法

朱 俊1,3, 陈长伟2

(1.金陵科技学院 计算机工程学院， 南京 211169； 2.南京晓庄学院 信息工程学院， 南京 2111711；3.江苏省社会安全图像与视频理解重点实验室(南京理工大学)， 南京 210094)

为了提高图像重建的质量，基于压缩感知理论，提出了一种基于总变差和组稀疏性的图像重建方法，同时考虑图像像素灰度值的梯度稀疏性和重叠图像块的非局部相似性两种先验知识。为了准确挖掘先验知识，本文选择非凸lp范数描述，并利用交替方向乘子法求解产生的重构模型。实验结果表明，与当前主流的重建算法相比，所提算法能够获得更高的图像重构结果。

压缩感知；总变差；组稀疏性；交替方向乘子算法

压缩感知(Compressive Sensing，CS)理论[1]能够以非常少的采样数目准确重构出原始信号，采样数目远远少于传统奈奎斯特采样定理所需求的数量(信号带宽的两倍以上)，因此CS技术逐渐取代了传统的采样和恢复方法，成为图像处理领域的热门研究方向，并且广泛的应用在卫星遥感、医学成像等多个领域。

图像作为现实中频繁使用、结构复杂的一种二维信号，如何准确重构出图像信号是近年来压缩感知理论应用的研究热点和难点。传统的思路是挖掘图像在某一字典下的稀疏性先验[2]。字典选择的合适与否直接影响着图像的重建质量，自适应字典可以好的重建结果，但是学习自适应字典需要一定的复杂度开销。图像中都会存在或多或少的相似结构，如果对图像进行分块处理，那么对一个参考图像块来说，在图像中的不同位置上可以找到跟它相似的许多图像块。因此，许多学者基于上述先验设计出了许多更优秀的压缩感知算法[3-5]，实验也证明这些算法的有效性。董伟生等提出了一种基于非局部低秩约束的图像压缩感知重建算法，利用非局部相似图像块构成的群组矩阵的低秩性，进而重建图像。张健等提出了一种基于组稀疏性的图像复原方法，约束构造的群组矩阵满足组稀疏性，既考虑了单个图像块的稀疏性，又考虑了相似块稀疏表示系数之间的关系，在图像复原领域取得了很好的效果。

为了获得高质量的重建图像，本文基于压缩感知理论，提出了一种基于总变差和群组稀疏性的图像重建方法，同时考虑图像像素灰度值的梯度稀疏性和重叠图像块的非局部相似性两种先验知识。为了准确挖掘先验知识，本文选择非凸lp范数描述，并利用交替方向乘子法求解产生的重构模型。实验结果表明，本文算法可以显著提高图像重构质量，峰值信噪比优于其他算法0.86 dB以上。

1 基于总变差和组稀疏性的图像压缩感知重建算法

1.1模型构造

令图像为x∈Rn，测量矩阵为Φ∈5m×n(mlt;lt;n), 压缩感知旨在从少量的测量值y∈Rm恢复出图像x。因为mlt;lt;n，因此存在无数多解x∈Rn满足y=Φx。为了准确重构出图像，需要利用图像的先验知识。本文提出了一种基于总变差和组稀疏性的图像压缩感知方法，同时考虑图像像素灰度值的梯度稀疏性和重叠图像块的非局部相似性两种先验知识，重建模型为

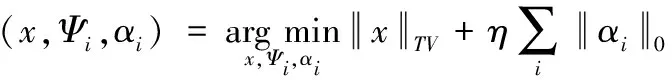
s.t.y=Φx,Pix=Ψiαi

(1)

其中Pix=[Pi1x,Pi2x,…,Pihx]表示由图像块xj∈Rd的h个相似块组成的群组矩阵，αi是群组矩阵在变换域Ψi下的稀疏表示系数，η是正则化参数。本文选择l0范数的总变差||x||TV=||Dx||0约束图像局部信息，其中D=[D1,D2]，D1和D2分别是横轴和纵轴的有限差分算子。因此，上式可以重新定义为：

s.t.y=Φx,Pix=Ψiαi

(2)

1.2 数值求解算法

由于式(2)很难直接求解，选择交替方向乘子算法将上述复杂问题转化成简单子问题，然后迭代求解这些子问题。添加辅助变量g，式(2)重新定义为：

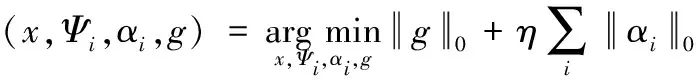
s.t.y=Φx,Pix=Ψiαi,g=Dx

(3)

引入拉格朗日乘子，上述约束问题的等价形式为

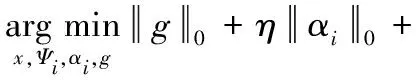
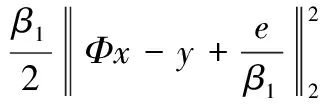
(4)

由于式(4)包含l0范数，它是一个非确定多项式问题，因此选择lq范数近似l0范数，上式转化为

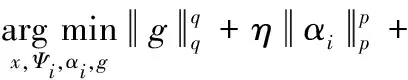
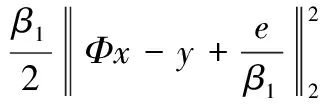
(5)

式(5)的优化包含如下三个子问题:

(6)

(7)

(8)

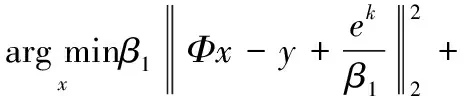
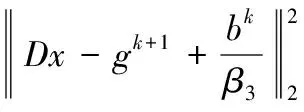
(9)

1.2.1g子问题

g子问题是一个非凸问题，无法获得全局最优解，但可以通过一种迭代加权方法去求解。令

(10)

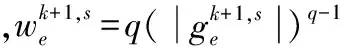
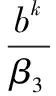
(11)

1.2.2Ψi子问题

由于固定的字典不能保证对所有的图像最优，因此，构造自适应的字典。受文献[15]的启发，对每个群组矩阵的估计值Pixk进行奇异值分解

Pixk=URV

(12)

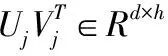
1.2.3αi子问题

类似于g子问题，采用相同的处理方式，可以得到如下的迭代解析解：

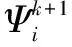
(13)

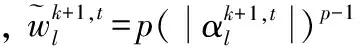
1.2.4x子问题

对x求导，令其导数为0，则图像x重建问题转化为

(14)

因此，可以获得图像估计值xk+1。

(15)

算法流程总结如下：

算法1 基于总变差和组稀疏性的图像压缩感知重建算法输入：测量矩阵Φ，测量向量y；初始化：x0=g0=b0=e0=c0=zeros(n，1)，Li=zeros(d，h)。主迭代：当图像x不满足收敛 (a)利用估计图像xk对每个图像块xki计算提取矩阵Pi；(b)通过式(11)估计gk+1；(c)通过式(12)估计Ψk+1i；(d)通过式(13)估计αk+1i；(e)通过式(15)估计xk+1；(f)更新拉格朗日乘子； bk+1←bk-τβ3(gk+1-Dxk+1)； ek+1←ek-τβ1(y-Φxk+1)； ck+1←ck-τβ2(Ψk+1iαk+1i-Pixk+1)；输出：估计图像x。

2 仿真实验

在本节中，通过多组实验来证明本文算法的优越性。选取6幅自然灰度图像Barbara、House、Lena、Cameraman、 Foreman、Parrots(如图1)进行测试，图像大小均为256×256。算法中的参数设置如下：采样率为m/n；群组矩阵的大小为36×45，即图像块的维数为36，对每一个参考图像块寻找45个最相似的图像块；沿着横轴和纵轴方向，每隔5个像素点选取重叠参考块xi∈Rd；图像的重建质量由峰值信噪比(PSNR)来评价，PSNR值越高，则重构图像与参考图像就越逼近，算法效果越好。

图1 六幅测试图像

将本文算法分别与总变差(Total Variation，TV)方法[16]，基于BM3D(Block Matching and 3D filtering，BM3D)的CS方法[17]，非局部低秩约束(Nonlocal Low-rank Regularization，NLR)方法[11]进行比较。TV方法是利用梯度域的稀疏性进行图像重建；BM3D是一种基于块匹配三维变换迭代收缩的图像重构算法，它是目前已公开发表文献中去噪性能优秀的算法之一；NLR方法利用图像非局部低秩先验知识，获得了当前文献中最好的重建结果。

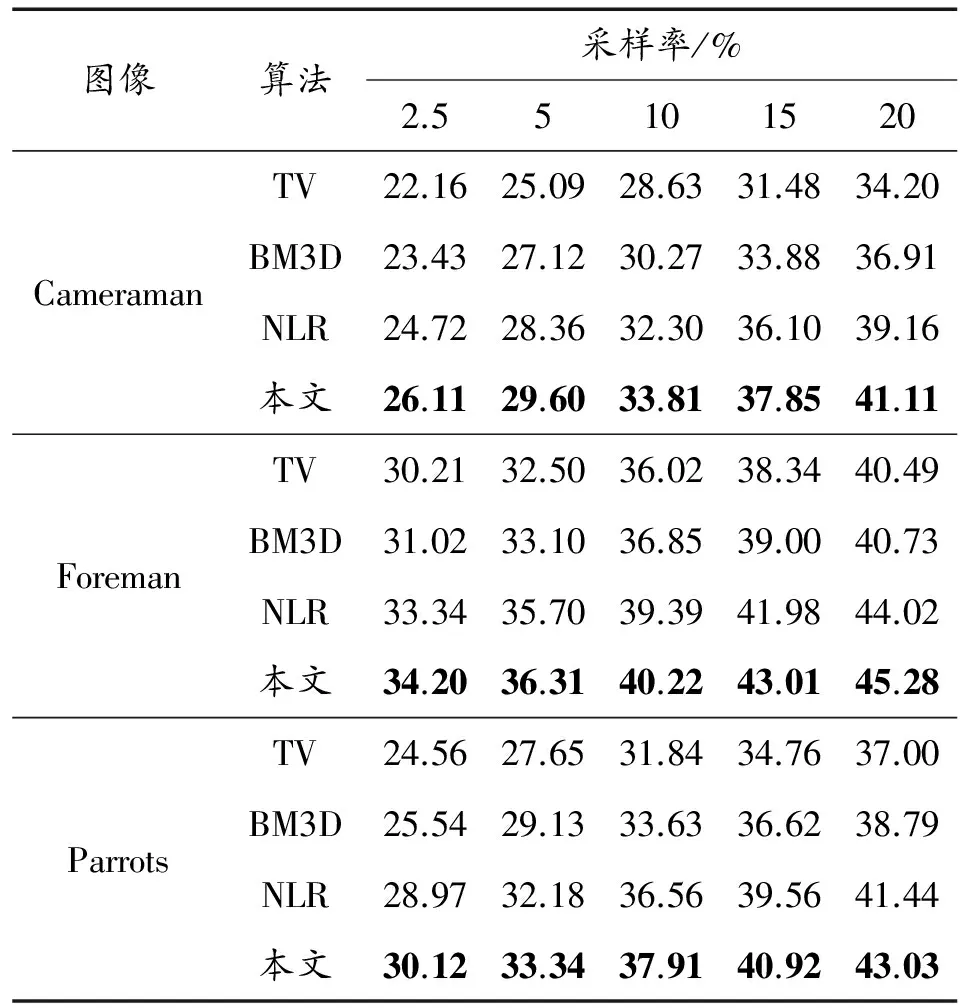
为了公平比较这些方法，调整每种算法的参数使得它们获得最优重构结果。本文方法测试20次取平均值。六幅测试图像在采样率分别为2.5%、5%、10%、15%、20%的重建结果如表1所示。由表1可以看出，1)TV重构算法由于仅采用了图像的梯度稀疏先验，忽略了图像的非局部相似性，难以重建复杂纹理信息。虽然BM3D重构算法的PSNR值明显高于TV算法，但在边缘部分的失真非常大，而且每次迭代过程中会引入噪声，所以比NLR算法和本文算法低；2)本文算法同时考虑了图像的梯度稀疏性和组稀疏性两种先验知识，获得了最好的重构结果，相比其他算法平均至少有0.86 dB的提升；3)在测试图像Foreman上，采样率为20%的情况下，本文算法的PSNR值分别比TV、BM3D和NLR高出7.67 dB、4.67 dB和1.67 dB。

表1 不同算法在不同图像上的峰值信噪比

图像算法采样率/%2．55101520CameramanTV22．1625．0928．6331．4834．20BM3D23．4327．1230．2733．8836．91NLR24．7228．3632．3036．1039．16本文26．1129．6033．8137．8541．11ForemanTV30．2132．5036．0238．3440．49BM3D31．0233．1036．8539．0040．73NLR33．3435．7039．3941．9844．02本文34．2036．3140．2243．0145．28ParrotsTV24．5627．6531．8434．7637．00BM3D25．5429．1333．6336．6238．79NLR28．9732．1836．5639．5641．44本文30．1233．3437．9140．9243．03

图2 图像Barbara在2.5%采样率下的重建结果

图3 图像House在2.5%采样率下的重建结果

图4 图像Foreman在2.5%采样率下的重建结果

3 结论

本文在利用图像总变差的基础上，提出了基于总变差和组稀疏性的压缩感知图像重建算法，同时挖掘图像像素灰度值的梯度稀疏性和重叠图像块的非局部相似性两种先验知识，并选择非凸lp范数近似l0范数准确挖掘先验信息。另外，选择交替方向乘子法将复杂的优化模型分解成多个简单的子问题，准确求解产生的非凸优化问题。实验结果表明，与主流的重建算法相比，本文算法在客观指标PSNR和主观视觉效果方面都有显著地提高。

[1] DONOHO D L.Compressed sensing[J].IEEE Trans.Inf.Theory.2006,52(4): 1289-1306.

[2] FENG L,SUN H.Blind compressive sensing method via local sparsity and nonlocal similarity[J].Journal of Nanjing University of Science amp; Technology,2017,41(4):399-404.

[3] FENG L,SUN H,SUN Q,et al.Compressive sensing via nonlocal low-rank tensor regularization[J].Neurocomputing,2016,216(C):45-60.

[4] FENG L,SUN H,SUN Q,et al.Image compressive sensing via truncated schatten-p,norm regularization[J].Signal Processing Image Communication,2016,47:28-41.

[5] 朱俊,陈长伟,苏守宝等.基于局部和非局部正则化的图像压缩感知[J].数据采集与处理,2016(6):1148-1155.

(责任编辑杨继森)

CompressiveSensingReconstructionMethodViaTotalVariationandGroupSparstiy

ZHU Jun1，3, CHEN Changwei2

(1.Jinling Institute of Technology College of Computer Engineering, Nanjing 211169, China; 2.Information Engineering Institute, Nanjing Xiaozhuang University, Nanjing 211171, China;3.Key Laboratory of Image and Video Understanding for social Safety (Nanjing University of Science and Technology), Nanjing 201194, China)

In order to improve the quality of the recovered image, based on the theory of compressive sensing (CS), this paper proposes a total variation and group sparsity based image reconstruction method toward exploiting the local gradient sparsity of image pixels and nonlocal similarity of overlapped image patches. In order to accurately exploit the prior knowledge, this paper selects nonconvexlpnorm and takes alternating direction method of multipliers method (ADMM) to solve the resulting nonconvex optimization model. The experimental results have demonstrated that the proposed approach outperforms current mainstream CS algorithms.

compressive sensing (CS); total variation; group sparsity; alternating direction method of multipliers

2017-08-20；

2017-09-10

金陵科技学院博士启动金项目“基于聚类融合特征配准图像鲁棒拼接算法”(Jit-b-201508); 江苏省社会安全图像与视频理解重点实验室创新基金项目(30916014107)；江苏省高等学校自然科学研究面上资助项目(16KJB520014)

朱俊(1981—)，男，博士研究生，讲师，主要从事模式识别、图像特征处理研究。

信息科学与控制工程

10.11809/scbgxb2017.11.025

本文引用格式：朱俊，陈长伟.结合总变差和组稀疏性的压缩感知重构方法[J].兵器装备工程学报，2017(11):114-117,128.

formatZHU Jun, CHEN Changwei.Compressive Sensing Reconstruction Method Via Total Variation and Group Sparstiy[J].Journal of Ordnance Equipment Engineering,2017(11):114-117,128.

TN911.73

A

2096-2304(2017)11-0114-04