串级控制系统两步整定法的仿真研究

杨海勇

摘要：过程控制系统的PID参数整定问题，是系统运行过程中的重要问题，只有合适的PID参数，才能确保系统具有较高的控制质量。本文介绍利用仿真软件MATLAB/Simulink对串级控制系统的参数整定进行仿真研究的方法和步骤，具体给出了串级系统的仿真模型，按两步整定法，结合每一步中所用的经验凑试法，得出控制质量良好的仿真结果。

关键词：串级系统；两步整定法；MATLAB仿真

一、引言

过程控制作为自动化的一个重要方向，其控制策略是非常丰富的，在过程控制实际工程应用中，不仅要选用恰当的控制方案，还需要整定好调节器的 PID参数，才能得到令人满意的控制质量。因此，整定PID参数，是系统投运后的重要事项，需要我们足够的重视，相关的整定方法有两种。

理论计算法需要获取对象的动态特性，采用频率特性法或根轨迹法等计算，费时费力，在工程实际中并不适用。工程整定法是一种相对比较方便实用的方法，无需对象的特性，可以在闭合回路中整定，包括衰减曲线法、凑试法。

在具体过程控制的教学和实训时，因为过程控制生产设备的安全性要求和限制，使得控制器的参数整定方法并不能实际操作训练；而过程控制实验装置的小型化简易化，则使得参数整定的实验效果不理想。利用仿真技术的快捷有效，可以解决这类参数整定问题，有助于我们高效的学习训练。

单回路系统的衰减曲线法和经验凑试法是基础整定方法，相关仿真研究已经比较多，这里只作简要介绍。本文主要针对串级系统，利用MATLAB软件，对两步整定法进行分析仿真。

二、常用整定方法简介

衰减曲线法和凑试法都是单回路系统的主要整定方法，两种方法的首要步骤很相似，都是在纯比例作用下，给定值为阶跃扰动，将系统投入闭环运行，并逐步增大比例控制作用（即增大 Kp），直到得到衰减比为 4：1的响应曲线。一般认为，衰减率为0.75的系统的稳定性已经足够，此时衰减比为4：1，能达到整定要求。

后续对于衰减曲线法，是根据第一步记录下来的比例带以及衰减周期 ，查询相关的数据经验表，再求出δ、Ti 、Td三者的参数值。

对于经验凑试法，则是逐步加入适当的积分作用和微分作用，看响应曲线的表现调整PID参数，直到达到较高的控制质量。当然，这种方法比较灵活快速，但需要一定的熟练经验。

三、两步整定法的仿真

MATLAB是当前应用广泛的仿真软件， Simulink则是 MATLAB内嵌的一个功能完善的仿真建模环境，因为内含大量标准功能模块，能快捷地根据需要选用模块并构成仿真模型。

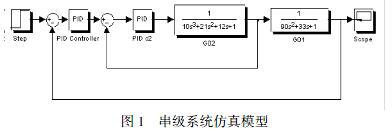
在MATLAB软件正常运行后，利用Simulink 命令打开库浏览器，再创建一个新的空白模型窗口。在各个子模块库中，根据需求，选出相关的各个标准模块，拖进新建窗口中，按图1所示连接，构成串级控制系统的模型。

图1中的Step模块的阶跃值设成1，作为系统的给定值信号。 用到的PID 模块并不在Simulink的标准库里，而是在附加库里，即Simulink Extras 库里的 Additional Linear 子模块库中。PID 模块内的三个参数分别为Kp、Ki、Kd，系数越大，相关控制作用越强。

对串级系统来说，按照两步整定法操作比较合适，具体方法是首先只针对副回路，整定好PID参数，再将副回路看成整体中的一个部分，只针对主回路，对主调节器参数进行整定。

具体在每一步每个回路的参数整定方法，都還是按基本的单回路系统的参数整定方法，具体如4：1衰减曲线法或者经验凑试法，本文采用更接近工程实际应用的经验凑试法，这样可以避免烦琐的计算，加快参数调试的速度。

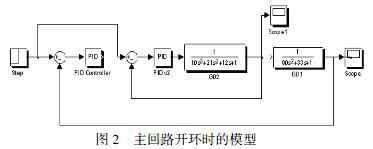
第一步，将主回路处于开环状态，只针对副回路，按照衰减曲线法，整定副调节器参数。构造的模型见图2。

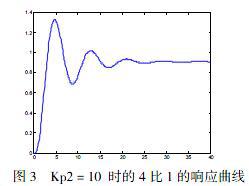
不断试验，逐步调大副调节器的 Kp值，当 Kp2=10， 可以得到衰减比为4比1的响应曲线，见图3。这里的副调节器一般只选用比例控制规律就足够了，不用加入积分和微分控制规律， 因此设置积分系数 Ki2=0，微分系数 Kd2=0。

第二步，主回路闭环时，见图1。 此时按前面的整定结果，将参数设置为 Kp2=10， Ki2=0， Kd2=0，然后只针对主回路，整定其中的PID参数。

不断试验，当主调节器的Kp1 = 13 时，得到的响应曲线大约为4比1的衰减比，符合要求。 然后用凑试法加入适当积分作用Ki1=0.125后，仿真结果如图4所示，此时的超调量还是很大，控制效果不够理想。

为了进一步减小超调量，接下来考虑应该减小比例控制作用。经过不断调小Kp1参数并仿真实验，当Kp1 = 4， Ki1=0.125 ， 能大幅减小超调量，控制质量有所提高。

最后加入适当微分作用，Kp1 = 4， Ki1=0.125 ， Kd1 = 2， 仿真结果见图5。

从图5可以看出，系统的响应速度快，在较短的过渡过程时间内趋于稳定，没有余差，超调量约为2%，说明这个串级系统取得了预期的较好整定效果。

四、结语

利用MATLAB软件对串级控制系统的两步整定法进行仿真研究，步骤清楚，方法可靠，能得出良好的仿真结果，适用于过程控制课程的课堂教学演示和实验，也可以用于相关过程控制系统的培训工作。

参考文献：

[1]王正林，郭阳宽. 过程控制与SIMULINK应用[M]. 北京：电子工业出版社，2006.

[2]邵裕森，戴先中. 过程控制工程[M]. 北京：机械工业出版社，2000.

[3]李国勇，程永强. 计算机仿真技术与CAD [M]. 北京：电子工业出版社，2012.