基于等效磁路法的轴向磁场磁通切换型永磁电机静态特性分析*

徐 妲, 赵旭鸣, 林明耀, 付兴贺, 郝 立, 李欣哲

(1. 东南大学 电气工程学院,江苏 南京 210096;2. 国家电网江苏省电力公司检修分公司,江苏 南京 210096;3. 国家电网江苏省无锡供电公司,江苏 无锡 214100)

基于等效磁路法的轴向磁场磁通切换型永磁电机静态特性分析*

徐 妲1, 赵旭鸣2, 林明耀1, 付兴贺1, 郝 立1, 李欣哲3

(1. 东南大学 电气工程学院,江苏 南京 210096;2. 国家电网江苏省电力公司检修分公司,江苏 南京 210096;3. 国家电网江苏省无锡供电公司,江苏 无锡 214100)

轴向磁场磁通切换型永磁(AFFSPM)电机是一种轴向长度短、转矩密度高的新型永磁电机。该电机磁场呈三维分布，与径向磁场电机不同，需要对该电机进行三维有限元分析，从而增加了电机分析和优化时的计算时间和成本。基于等效磁路法分析了AFFSPM电机的静态特性，建立了AFFSPM电机的非线性等效磁路模型，采用该模型计算、分析了气隙磁密、空载永磁磁链、反电动势和电感等特性，并与采用三维有限元方法的计算结果进行比较，验证了AFFSPM电机等效磁路模型的准确性，表明等效磁路模型适用于AFFSPM电机初始设计和分析。

轴向磁场；磁通切换；等效磁路法；电磁特性

0 引 言

双定子或双转子结构的轴向磁场磁通切换型永磁(Axial Field Flux-Switching Permanent Magnet,AFFSPM)电机因其结构紧凑、体积小、工作稳定、转矩密度高和效率高等优点备受国内外研究人员的关注和研究[1-7]。AFFSPM电机较短的轴向长度使得该电机更适用于直接驱动控制系统如风力发电、电动汽车等。

电机静态特性的准确分析是电机设计和优化的前提条件。目前分析电机电磁性能的计算方法主要为数值法和解析法。其中，解析法计算繁琐，需要推导大量公式，并在特定的简化条件下求解方程组，而计算过程中诸如磁路饱和、漏磁等因素无法精确地考虑在解析式中，导致计算准确度较低，一般只用于定性分析。故定量分析时一般采用数值法，常用方法包括有限元法和等效磁路法。三维有限元法可同时考虑多种效应的影响，结合功能强大的有限元计算软件，实现精度较高的电磁场分析，但分析计算时间较长，较适合对于结构参数已确定的电机进行分析计算，对于需要多次计算不同结构参数下的初始设计和静态特性分析来说，有限元法较不便且计算成本较高。等效磁路法是电机工程中常用的磁场近似计算方法，将场化路，可以兼顾磁路饱和、永磁及电枢磁场相互作用等影响，实现电机磁场分布和参数的快速求解，适用于电机初始设计。等效磁路法在不同类型永磁电机的电磁设计中应用广泛[8-14]。文献[9-10]基于等效磁路模型对径向磁场磁通切换电机的电磁特性进行研究。文献[11-14]对轴向磁场表贴式盘式电机的等效磁路模型进行了研究和优化。

与径向磁场类型的电机不同，AFFSPM电机的转子旋转方向与永磁磁通方向垂直，且同时存在轴向和周向路径的磁通，电机磁场呈三维非线性分布，难以将其简化为二维磁场分析计算，使得其分析设计过程难度加大。因此，对于AFFSPM电机来说，电机的性能预估分析和优化设计需建立一个简单、准确的等效磁路模型。

本文针对三相12/10极AFFSPM电机，推导并建立该电机的考虑磁路饱和以及气隙漏磁影响的等效磁路模型。在等效磁路模型的基础上，求解、分析该电机的静态特性，包括气隙磁密、空载永磁磁链、反电动势和绕组电感，并将计算结果与三维有限元法分析结果进行对比验证。

1 电机结构

AFFSPM电机由两个定子和一个转子组成，如图1所示，转子置于中间，与两个外定子形成双气隙。12/10极AFFSPM电机每个定子由12个U型铁心、12块永磁体和12个线圈组成。线圈绕于两个相邻U型铁心齿上，中间嵌入永磁体，每4个线圈串联成一相绕组。单个定子上永磁体沿切向交替充磁，两侧定子正对的永磁体充磁方向相反。电机转子无磁轭，结构与开关磁阻电机类似。10个转子齿均匀设置在非导磁圆环的外圆周上，转子齿为卷绕式冲片叠压而成。该电机轴向长度短，槽满率高，具有较高的功率密度和效率。

图1 三相12/10极AFFSPM电机结构图

2 等效磁路模型

等效磁路法适用于不同类型电机的磁场近似计算。对于AFFSPM电机来说，其等效磁路模型包括定子铁心、永磁体、转子铁心和气隙4个部分。AFFSPM电机的盘式结构使得磁通密度沿径向近似均匀分布，故电机的静态特性可以简化在平均半径处计算。

图2 定、转子铁心与永磁体等效磁路模型

定、转子铁心和永磁体的局部等效磁路模型如图2所示。考虑磁路饱和的影响，铁磁材料采用非线性磁阻Rsy、Rst、Rrt。定子齿槽之间的漏磁通以及端部漏磁由磁阻Rstl1、Rstl2和Rstl3体现；转子齿距较长，其齿间漏磁通不予考虑。等效磁路模型中永磁体等效为磁动势源Fm和内磁阻Rm，同时采用漏磁阻Rml体现永磁体端部漏磁。对于定、转子铁心来说，其相对磁导率随铁心内磁通密度而变化，故等效磁路建模过程中依据软磁复合材料的磁化曲线进行迭代计算非线性磁阻，从而考虑磁路饱和现象。

以上各磁阻和磁动势可由式(1)～式(9)计算：

式中:μ0、μr——真空磁导率、相对磁导率；

hst、hm、hsc、hrt——定子齿宽、永磁体磁化厚度、定子单元宽度、转子齿宽，如图3所示；

le——AFFSPM电机径向有效长度，定义为le=(Dso-Dsi)/2；

ls、lsy、lst——定子轴向长度、定子轭部厚度、定子齿轴向长度；

lr、g——转子轴向长度、气隙长度；

Ps——定子单元数;

Dso、Dsi——定子外径、内径；

HC、Br——永磁体矫顽力、剩余磁通密度。

图3 AFFSPM电机结构参数标示

在AFFSPM电机等效磁路模型中，定、转子之间的气隙磁阻是关键参数。由于空气的磁导率远远小于导磁材料的磁导率，气隙磁阻的计算精度对电机等效磁路模型的准确性有很大影响。AFFSPM电机是双凸极结构，定、转子齿间存在明显的边缘效应和局部饱和现象，且与定、转子齿的相对位置、电枢绕组电流大小相关，因此气隙磁阻很难用数学式精确表达。

从计算精度和实用性角度考虑，本文采用分割法研究AFFSPM电机的气隙磁阻近似表达式。根据AFFSPM电机气隙磁场的分布规律，利用磁力线把AFFSPM电机气隙分成若干规则形状的磁通管，并使各个磁通管中的磁力线规律尽可能相同，如图4所示。在满足一定计算精度的情况下，假定气隙磁通仅沿着轴向分布，即垂直进入定、转子铁心端面。求出图4中各个磁通管的磁阻后，根据各个磁阻之间的串、并联关系可得整个气隙的总磁阻。根据电机转子转动过程中所在的位置，将转子位置划分为若干个区间，如图5所示。每个区间内磁通分布规律基本一致，故区间内气隙磁阻可根据相同磁阻公式进行计算。定转子齿间气隙磁阻可以表示为基本气隙磁阻类型的组合，根据各磁通管的形状参照基本类型的公式进行计算[9]。

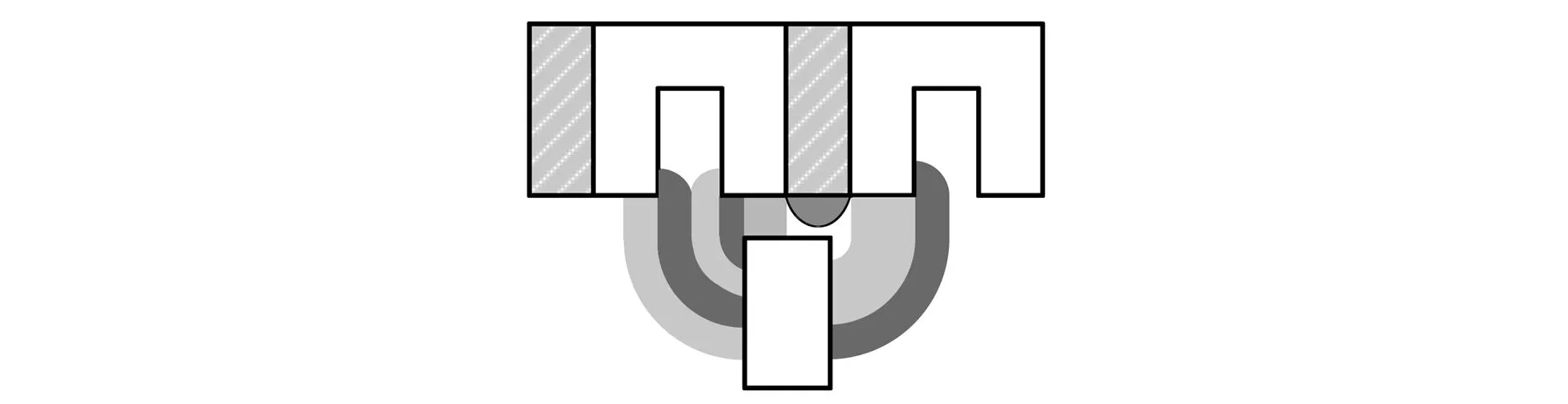
图4 气隙磁阻组成局部示意图

图5 电机转子位置区间划分示意图

根据AFFSPM电机的磁场分布和磁导分类，将以上各个不同部分的等效磁路结合在一起，可建立AFFSPM电机的等效磁路模型，如图6所示。

图6 局部结构等效磁路图

AFFSPM电机等效磁网络中，等势面的磁势节点位置可分别固定在定子和转子中，与转子位置角θr无关，也即定、转子极间磁通路径的改变可等效为定、转子极磁势节点之间的并联支路发生改变，这样转子运动过程中定子、转子的等效磁网络不需要重新建立。

3 静态特性分析与验证

通过对AFFSPM电机等效磁网络的求解，可以得到电机的静态特性，包括气隙磁密、空载永磁磁链、反电动势和绕组电感。为了验证上述等效磁路模型的准确性，对AFFSPM电机采用Ansys有限元分析软件进行仿真，并与等效磁路分析结果进行比较。电机主要结构参数如表1所示。

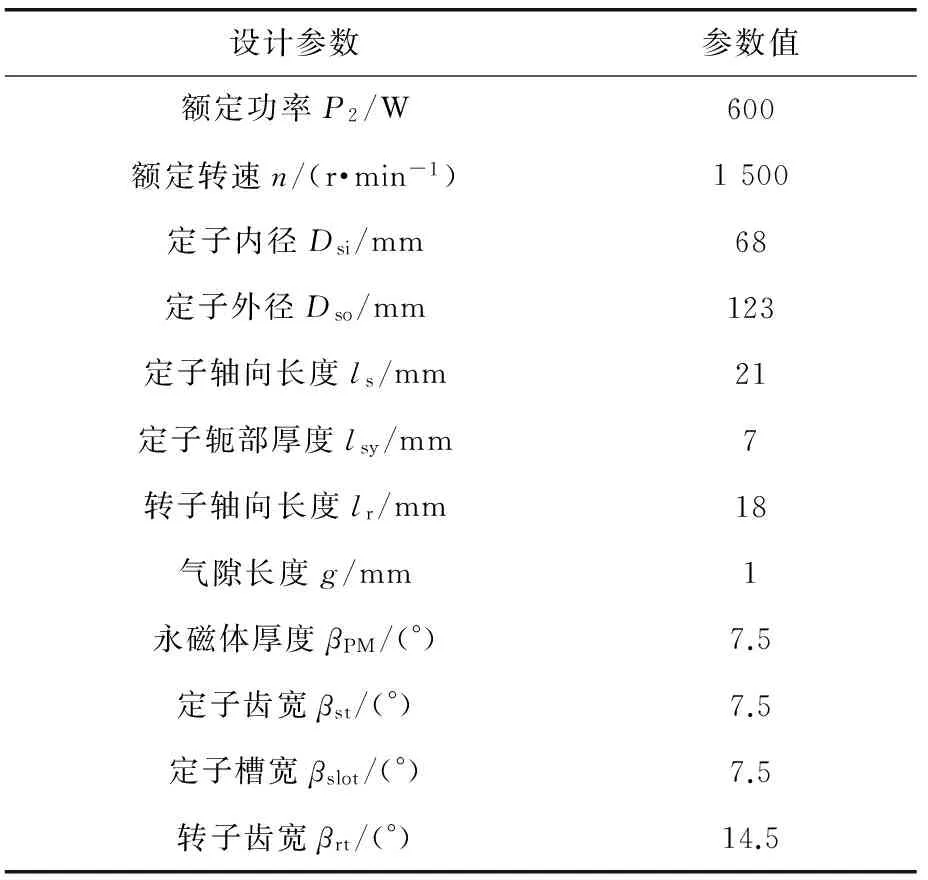
表1 AFFSPM电机结构参数

3.1气隙磁密

气隙磁通密度分布对电机特性分析很重要，图7为由有限元法和等效磁路法计算得到的半个圆周上平均半径处气隙磁密分布情况。由图7可见，磁路法分析与有限元分析的波形基本重合，峰值处数值有所差别，磁路法计算的磁密峰值比有限元计算结果略高,这是由于等效磁路法建模过程中假设气隙磁通均为垂直转子齿面(即轴向分布)且进行二维计算，有限元分析时对于AFFSPM建立了三维有限元模型，实际平均半径处气隙磁通存在其他方向的分量。

图7 半圆周平均半径处空载气隙磁密

3.2空载永磁磁链

对于AFFSPM电机来说，以A相为例，单相绕组的空载永磁磁链ΦpA为

ΦpA=ΦA+ΦA′=

式中:ΦA、ΦA′——定子1、2上A相绕组的磁链；

ΦA1、ΦA2、ΦA3、ΦA4、ΦA1′、ΦA2′、ΦA3′、ΦA4′—— 定子1、2上A相绕组每个线圈的磁链。

图8所示为由有限元法和等效磁路法计算得到的A相绕组空载永磁磁链波形。两种方法分析的结果基本吻合，等效磁路法计算所得的磁链幅值比有限元分析所得结果略大，在可接受的误差范围内。两者偏差原因是假定气隙磁通仅沿着轴向分布所致，引入漏磁系数可使计算结果更为精确。

图8 单匝空载永磁磁链

3.3空载反电动势

A相反电动势由A相磁链求导可得：

如图9所示为由有限元法和等效磁路法计算得到的A相绕组空载反电动势波形。两种方法计算结果基本重合，但在反电动势峰值位置，等效磁路法的计算值明显低于有限元法的计算值。此外，磁路法计算所得反电动势谐波含量较高，使得波形平滑度明显低于有限元法分析结果。

图9 单相空载反电动势

3.4电感特性

以A相为例，AFFSPM电机电枢相绕组的自感La和互感Man的计算方法如下：

式中:ΦpmA——A相绕组匝链的空载永磁磁链；

ΦpA——某相绕组通入电流后A相绕组匝链的磁链；

ia、in——A相和B相(或C相)绕组通入的电流。

图10为由有限元法和等效磁路法计算得到的A相绕组不饱和电感和饱和电感波形。由图10可见，两种方法计算所得的A相绕组不饱和自感和互感的波形具有较好的一致性，而磁路法计算所得的A相绕组饱和自感和互感均低于有限元法分析结果，电感的计算结果与磁通计算值相关。

图10 相绕组自感和互感

4 结 语

本文基于等效磁路法提出了三相12/10极AFFSPM电机的简单而准确的磁场计算模型。该模型考虑了铁心磁路饱和以及各部分漏磁的影响。对于铁心饱和的影响，该模型采用迭代法计算非线性铁心磁阻；对电机定转子各部分分别建立磁路模型，通过改变气隙串联磁路来反映电机转子运动过程中气隙磁场的分布，有效简化等效磁路模型。在电机等效磁路模型的基础上，求解了电机的静态特性，包括气隙磁密、空载永磁磁链、反电动势和电枢绕组电感。将三维有限元法分析结果与等效磁路法分析结果进行对比，验证了所建立的等效磁路模型的准确性。本文所建立的等效磁路模型能在保证较高计算精度的前提下，有效节省计算时间，适用于该种电机的初始设计和电磁优化，对其他类型的轴向永磁电机的分析设计有一定参考价值。

[1] LIN M Y, HAO L, LI X, et al. A novel axial field flux-switching permanent magnet wind power generator[J].IEEE Transactions on Magnetics,2011,47(10): 4457-4460.

[2] HAO L, LIN M Y, XU D, et al. Static characteristics of a novel axial field flux-switching permanent magnet motor with three stator structures[J].IEEE Transactions on Magnetics,2014,50(1): 1-4.

[3] HAO L, LIN M Y, LI W, et al. Novel dual-rotor axial field flux-switching permanent magnet machine[J].IEEE Transactions on Magnetics,2012,48(11): 4232-4235.

[4] ZHAO W L, LIPO T A, KWON B I. A novel dual-rotor, axial field, fault-tolerant flux-switching permanent magnet machine with high-torque performance[J].IEEE Transactions on Magnetics,2015,51(11): 1-4.

[5] 郝立,林明耀,徐妲,等.轴向磁场磁通切换型永磁电机齿槽转矩抑制[J].电工技术学报,2015,30(2): 21-26.

[6] KABIR M A, AHMED A, HUSAIN I. Axial flux segmental rotor flux-switching synchronous motor[C]∥ IEEE Conference on Energy Conversion Congress and Exposition (ECCE),2015: 2148-2152.

[7] 裴召刚,林明耀,赵纪龙,等.轴向磁场磁通切换型永磁电机矢量控制[J].电机与控制应用,2013,40(7): 37-42.

[8] 葛笑,张琪,黄苏融.磁极分割型混合励磁电机等效磁路法分析[J].电机与控制应用,2006,33(1): 11-16.

[9] ZHU Z Q, PANG Y, HOWE D, et al. Analysis of electromagnetic performance of flux-switching permanent magnet machines by non-linearadaptive lumped parameter magnetic circuit model[J].IEEE Transactions on Magnetics,2005,41(11): 4277-4287.

[10] WEI H, GAN Z, MING C, et al. Electromagnetic performance analysis of hybrid-excited flux-switching machines by a nonlinear magnetic network model[J].IEEE Transactions on Magnetics,2011,47(10): 3216-3219.

[11] QU R H, LIPO T A. Analysis and modeling of air-gap and zigzag leakage fluxes in a surface-mounted permanent magnet machine[J].IEEE Transactions on Industrial Applications,2004,40(1): 121-127.

[12] 黄允凯,周涛.基于等效磁路法的轴向永磁电机效率优化设计[J].电工技术学报,2015,30(2): 73-79.

[13] KANO Y, KOSAKA T, MATSUI N. A simplenonlinear magnetic analysis for axial-flux permanent-magnet machines[J].IEEE Transactions on Industrial Electronics,2010,57(6): 2124-2138.

[14] 宫晓,徐衍亮.轴向磁场盘式永磁电机等效磁路网络及气隙漏磁的分析计算[J].电机与控制学报,2013,17(10): 59-64.

ElectromagneticPerformanceAnalysisofAxialFieldFlux-SwitchingPermanentMagnetMachineUsingEquivalentMagneticCircuitMethod*

XUDa1,ZHAOXuming2,LINMingyao1,FUXinghe1,HAOLi1,LIXinzhe3

(1. Department of Electrical Engineering, Southeast University, Nanjing 210096, China;2. Jiangsu Electric Power Maintenance Branch Company, State Grid, Nanjing 210096, China;3. Wuxi Power Supply Company of Jiangsu Province, State Grid, Wuxi 214100, China)

Axial field flux-switching permanent magnet (AFFSPM) machine was a novel machine with short axial length and high torque density. The 3-D distributed magnetic flux of the AFFSPM machine required the 3-D field analysis which increased the calculation time and cost of analysis and optimization. A nonlinear equivalent magnetic circuit model of the AFFSPM machine was built, and the static characteristics of the AFFSPM machine, including the air-gap flux density, permanent magnetic flux linkage, back electromotive force and inductance characteristics were calculated and analyzed based on equivalent magnetic circuit model. The calculated results were compared with those predicted by 3-D finite element method. The analysis results with two methods consist well, the feasibility of the proposed equivalent magnetic circuit model were verified.

axialfiled;flux-switching;equivalentmagneticcircuit;electromagneticperformance

国家自然科学基金项目(51277025，51577024)；江苏省自然科学基金项目(BK20161425)

徐 妲(1989—)，女，博士研究生，研究方向为永磁电机设计、分析。赵旭鸣(1987—)，男，硕士，中级工程师，研究方向为电机设计，电网运维。林明耀(1959—)，男，教授，博士生导师，研究方向为电机系统及其控制技术。

TM 301.2

A

1673-6540(2017)11- 0079- 06

2017 -03 -14