面向线性光谱混合分解的邻域像元集螺线型构建方法

刘博宇，陈 军，邢华桥,3，武 昊，张 俊

1.吉林大学地球探测科学与技术学院，吉林 长春 130026; 2.国家基础地理信息中心，北京 100830; 3.中国矿业大学(北京)地球科学与测绘工程学院，北京 100083

面向线性光谱混合分解的邻域像元集螺线型构建方法

刘博宇1,2，陈 军2，邢华桥2,3，武 昊2，张 俊2

1.吉林大学地球探测科学与技术学院，吉林 长春 130026; 2.国家基础地理信息中心，北京 100830; 3.中国矿业大学(北京)地球科学与测绘工程学院，北京 100083

高时间分辨率遥感影像在地表景观破碎区域易形成混合像元，难以发挥其高时间维度优势。现有方式多是基于线性光谱混合模型，借助邻域像元所构成的像元集合组成线性方程组，求出组分光谱值的最小二乘解，提高其空间分辨率。然而，现有方法依赖窗口形式来构建邻域像元集合，在某些区域易造成方程组无解的欠定问题。本文在分析其问题原因的基础上，引入阿基米德螺线代替传统的矩形窗口，对邻域各像元依次遍历，构建空间邻近、组分相近的邻域像元集合来解决该问题。在GlobeLand 30数据上的试验表明，螺线型构建方法对5种混合尺度上多种类型地物均具有稳定的精度，与传统窗口构建方法相比，可从构建邻域像元集合方面将总体理论精度提高2%,分解结果精度提高近1个数量级。

线性光谱混合分解;混合像元;邻域像元;螺线;窗口

环境变化监测、地表覆盖数据更新、土地资源动态管理等迫切需要兼具高时间和高空间分辨率的遥感影像[1-3]，但限于运行轨道、硬件等因素制约，遥感传感器还难以同时满足该高分辨率需求[4-5]。国内外通常是借助高空间分辨率的地表分类图，对多期低空间分辨率影像分别进行光谱分解，进而组成高空间分辨率影像序列[6-9]。设低空间分辨率像元P的光谱值为SP，对应高空间分辨率地物组分为Ci(i=1,2,…,n),其光谱值为SC，光谱分解是将SP看作由n个SC混合而成，基于表征两者之间关系的光谱混合模型，由SP推算出对应的SC[10-12]。常用的线性光谱混合分解方式是基于地理学第一定律。假设邻近地物有较强相关性，取当前和邻近的m个像元，构建其光谱值SP与组分光谱值SC之间的线性方程组L，在观测数(像元数)m大于等于未知数(组分数)n的条件下，按最小二乘法求解出当前像元P内的SC[13-14]。然而，当邻近地物类别相差较大时，邻域内某些像元的组分明显不同于当前像元，属于无效观测，这往往致使L在观测数m大于未知数n时仍然引发导致SC无解的欠定问题。组成非欠定的光谱分解线性方程组，需确保所选择的邻域像元均为有效观测，邻域范围像元集合的构建是解决此问题的关键。

通常，邻域像元集主要采用规则窗口来构建[15]。例如，文献[16]直接使用以待分解像元为中心的窗口来收集邻域像元；在文献[16]的基础上，文献[17]通过结合空间距离权重，减小窗口中较远处的像元对中心待分解像元组分值的影响；文献[18]通过增加光谱权重，进一步改善了窗口内部参与解算的像元种类，以此来提高分解精度；文献[19]提出使用限制性最小二乘法来保障组分值位于合理区间；文献[4]采用了一个移动窗口来收集周围邻域像元，来处理影像场景内的不同地方的光谱可变问题,并通过减少解算的部分类数，使得窗口中像元数大于组分数，来保障顺利分解；文献[20]通过对比不同大小的窗体下的计算精度，先验性地确定最佳窗口，构建邻域像元集。窗口型的邻域像元集构建方法原理简洁而易于实现，其效率较高，获得了广泛的应用。然而，这些在窗口基础上作出的改进，以及在其后的分解中所采取的保障措施并不是构建邻域像元集的根本解决方案。究其原因，是由于窗口的覆盖形状难以顺应地物分布走势，在部分区域不能从邻域内界定出各组分相近像元分布的准确范围，从而引发欠定问题。

螺线是一种具有非规则空间形态的几何曲线[22-23]。相较于窗口，螺线更加贴近邻域周围的非规则地表。沿其展开的轨迹，根据当前像元内的组分分布，对其四周地物类别相近的像元范围可进行最佳逼近，可构建空间相邻、组分相近的邻域像元集合，有望在一定程度上解决欠定难题。本文第1节分析线性光谱分解理论将混合像元分解为组分值时面临的问题，揭示传统窗口邻域像元集构建方式的缺陷，提出基于螺线构建非欠定的邻域像元集合的解决思路；第2节介绍螺线在二维笛卡尔坐标系中的参数公式，推导出其在影像栅格空间上的离散化形式，进而提出螺线形式的邻域像元集合构建算法；第3节以GlobeLand 30地表覆盖数据产品为基础，对比不同像元混合尺度上螺线型方法与窗口方法的试验结果；最后，总结并指出有待进一步研究的问题。

1 相似地物的螺线逼近

1.1 问题分析

在线性光谱混合模型中，将混合像元的值R表达为该像元内部各种地类(组分)值r与各地类所占面积比例(丰度)f的线性组合，如式(1)(n为组分总数；ε为非线性残差)。基于已有的地表分类图提取得到丰度后，采用线性光谱混合模型将混合像元分解为组分值，即求解以r为未知数的式(1)的过程。

(1)

按方程组求解的一般要求，方程数m应大于等于未知数的数量n(式(2))，此时属于适定、超定问题，可用最小二乘方法求最优解；当m小于n时，会发生无唯一解的欠定问题，求不出未知数。对线性光谱分解过程而言，即需列出满足式(2)的多个线性方程，组成线性方程组(如式(3))。为此，通常是依据地理学第一定律的观点，收集待分解像元空间附近的其他像元共同组成邻域像元集合[13,20]，以构成待分解像元的解算线性方程组[24-26]。

m≥n

(2)

(3)

邻域像元集的窗口构建方式，就是收集一定矩形空间范围内的像元，组成邻域像元集合。窗口的数学形式如式(4)，大小为2s+1(s为自然数，一般以像元为单位)，l为其所能解算的最大组分数。已知地表分类图的l为确定值，由式(4)即可计算窗口大小。由于地物类型多样，分布形式复杂，邻近地物的相关性难以一致，使得邻域中的其他像元与待分解像元组分类型构成并不完全相同。这些像元增大了中心像元方程组的方程数m，使得常出现方程数m远多于组分数n，但仍然解不出组分值的情况。规则的窗口不能顺应地物的分布形状，造成其邻域像元集合中常出现与待分解中心像元组分无关的其他像元，增加了解算方程组中无效方程的规模，给组分值的解算带来困难；部分均质像元因受到其他像元多种组分的影响，增加了分解其组分光谱值的复杂性。图1示例列举了窗口构建邻域像元集的4类典型情况：①像元A包含森林、草地、耕地3种组分类型，窗口代入了人造地表组分类型，其邻域像元集组分与丰度分布如表1-1所示，以丰度为系数的解算方程组中混入了无关光谱，增加了方程组的分解难度；②像元B包含水体、湿地、耕地3种组分类型，其窗口代入了含有无关组分的像元d5，其对应的线性方程组无法分解d5内的组分，如表1-2所示；③像元C包含5种组分类型，其窗口可收集6个像元(即m为6)，其邻域像元集总共包含6种组分类型(即n为6)，但由于其周围像元均不包含人造和裸地类型的光谱，造成对应方程组无法分解这两类光谱值，如表1-3所示；④像元D仅包含耕地一种组分类型，其窗口引入了包括人造、草地其他无关组分的像元。

(4)

表1 图1中邻域像元集组分及丰度分布一览表(子表1-1、1-2、1-3、1-4分别对应A、B、C、D的邻域像元集)Tab.1 The endmembers and abundance of adjacent pixel sets in fig.1(sub-table 1-1，1-2，1-3，1-4 correspond to A，B，C，D) (%)

1⁃31⁃4序号像元编码耕地森林草地人造覆盖裸地水体序号像元编码耕地人造覆盖草地1C6095141201D100002a85423600172g793073a10801830003g8771224b832253100124g993525b96912120085h798206b10871030006h982180

1.2 螺线逼近

阿基米德螺线(本文简称螺线)是一种沿中心向外逐渐旋转展开而形成的曲线，呈现出非规则的几何形态(图2)。其形态更加贴近非规则的邻域地表(图3)，沿其几何轨迹可对邻域内周围分布有多种地物的地表进行逼近，适于对各种空间尺度大小的对象进行局部遍历，以螺线中心为起点，沿其展开轨迹，顺次遍历其周围各空间位置的对象。这种由近及远地遍历周围对象的方式，较符合地理学第一定律关于空间邻近地物相关的假设对选择邻近地物的要求。螺线的极坐标形式如式(5)，其中a为极径，极角θ属于[0，2π]区间。

ρ=aθ,a>0

(5)

图2 地表极坐标上的螺线Fig.2 Polar Archimedean spiral in land surface

在与图1相同背景下，图3示例采用螺线对像元A、B、C、D周围顺次遍历，在较近的区域选择出组分类型相近的像元。结合表2可知，在像元A周围，其构建的邻域像元集包含了均有耕地、林地、草地3种组分类型的A和a1、a2、b1、c1共5个像元，即其线性方程组的观测方程均为有效观测，观测数m为5，组分值未知数n为3，较窗口方法构建的线性方程组规模更小，易于解算；在像元B处，螺线构建的像元集避开了像元d5的影响，利用该方程组可更加高效地分解出其内的耕地、水体、湿地组分值；对像元C构建的邻域像元集还包含了该区域内最邻近的a10、b10、c10、c9共4个组分相关像元，其线性方程组能有效地解算出像元C的组分值；由于像元D内部仅含有一种耕地组分类型，螺线构建的邻域像元集仅包含一个D像元。

图1 窗口构建邻域像元集示例(该窗口大小为3，A、B、C、D为待分解像元，背景为地表分类图)Fig.1 A window-based construction example(window size is 3，A，B，C，D are low spatial pixel，background is a class map)

图3 螺线对地表各地物类别的逼近示例(沿螺线轨迹选定的其他像元用黑点标记)Fig.3 An example of fitting similar pixels with Archimedean spiral in land surface (the similar pixels labeled by black dot)

表2 图3中螺线逼近的邻域像元集组分及丰度分布一览表(A、B、C、D分别对应表2-1、2-2、2-3、2-4)Tab.2 The endmember and abundance of spiral-based adjacent pixel sets in Fig.3(sub-table 2-1,2-2,2-3,2-4 correspond to A,B,C,D) (%)

2⁃32⁃4序号像元编码耕地森林草地人造覆盖裸地序号像元编码耕地1C609514121D1002a1080183003b1087103004c108710575c9441915815

1.3 螺线型构建思路

在异质地表上,顾及地理学第一定律关于邻近地物相关性强的假设，以及光谱分解线性方程组的解算要求，生成栅格化的螺线轨迹，在当前像元的周围邻域内进行遍历，并判别像元组分的相关性，发展螺线型的邻域像元集构建算法，以此来构建空间邻近、组分相近的邻域像元集，是解决欠定问题的可取途径。

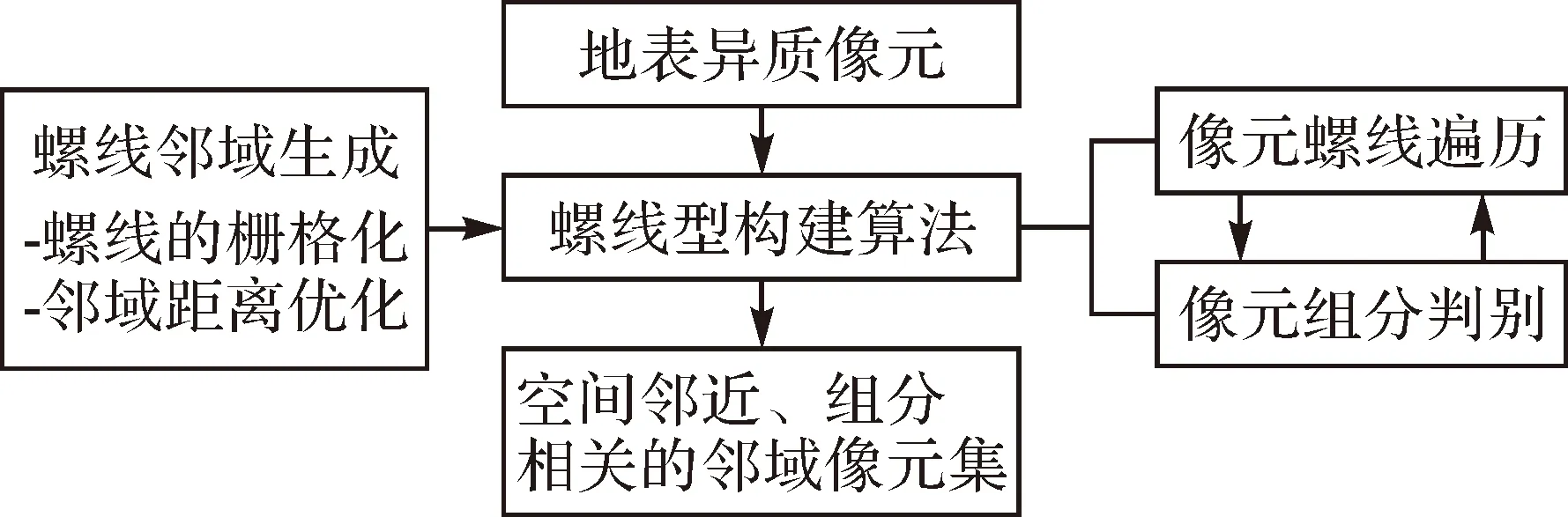
图4 基于螺线的领域像元集构建思路Fig.4 Strategy of constructing adjacent pixel sets with Archimedean spiral

2 邻域像元集的螺线构建

2.1 螺线轨迹的栅格化生成算法

遥感影像是以矩阵组织像元的栅格格式，研究螺线在二维笛卡尔坐标系下的离散化形式形式，有助于螺线在影像处理中的应用。在二维笛卡尔坐标系下，螺线极坐标公式的参数形式为式(6)，a=vt,θ=wt,v为线速度，w为角速度。

(6)

由式(6)可推导出螺线在矩阵空间上的离散化形式，如式(7)，r为半径，f1(θ)、f2(θ)为函数，如式(8)，θ为由0到2π周期性变化的角度，其定义域如式(8)和(9)所示，r是自然数,k为整数。由该离散化的螺线公式，以一个像元为单位，以某像元中心为螺线的原点， 沿其几何轨迹顺次确定出周围各像元的中心位置， 取其上离散化的整数为坐标值，周围邻域像元如图5(b)所示。

图5 螺线在二维笛卡尔坐标系向矩阵空间转换示例Fig.5 Archimedean spiral conversion from two dimensional Cartesian coordinate system to matrix system

(7)

(8)

2.2 基于螺线轨迹的邻域像元集生成

在低空间分辨率影像上，采用螺线构建邻域像元集，需按低空间分辨率影像与该区域地表分类图的空间位置，提取各像元范围内的组分类型C、组分数n和丰度f。螺线型算法的原理如图6所示，设邻域像元集中各像元丰度组成的矩阵为F,其秩记为rankF,其形式化描述如下：

第1步，在影像栅格上，建立每个像元P的邻域像元集SP，并将P加入SP。

第2步，以P为螺线中心，沿离散化的螺线顺次遍历P邻域内的其他像元P′。

第3步，判别P′内的组分类型C′，若均为相似组分则将其加入SP，进入下一步骤；否则，继续按当前的次序遍历。

第4步，判断当前邻域像元集的丰度矩阵的秩rankF是否等于待分解像元的组分数n,即rankF=n；若满足，则完成构建邻域像元集SP过程；否则，按当前次序顺次加1，继续第2步过程。

图6 螺线构建算法原理Fig.6 Archimedean spiral-based adjacent pixel sets construction approach

3 试验与分析

3.1 试验区与数据

采用30 m空间分辨率的2010期GlobeLand 30地表覆盖产品作为分类图，按混合像元分别为4、6、8、10和12倍于分类像元的混合尺度关系，检验了螺线型方法对混合像元构建领域像元集与分解时的精度及效率，并与窗口型方法相应结果对比。试验区是面积约为1300 km2的北京地区，其内部广泛分布有耕、林、草、灌丛等共8种地物类型(图7)。各尺度的混合像元值按式(1)残差为零，根据分类图生成，值域为[0.1,0.9]；由式(4)计算，窗口大小为3；螺线邻域像元集像元数规模设为中心像元组分数的2倍。

图7 GlobeLand 30北京区域地表覆盖图Fig.7 GlobeLand 30 class map in Beijing area

3.2 试验结果与分析

对试验区主要地表覆盖上的构建统计结果如图8所示。总体上，人造地表、水体与湿地、耕地、林地与灌丛分布区域的欠定像元比例，随混合尺度变大而逐渐增加；窗口型方法存在不同程度的欠定问题，且其比例随着混合尺度呈线性增加趋势；螺线型方法在各尺度上基本持平，均处于较低水平，说明其对多种尺度的混合像元均具有稳定的解算像元集合构建能力，可显著减少欠定问题的发生。综合5种混合尺度的欠定像元统计结果，窗口方法在构建非欠定的线性解算方程组方面精度约为97%，而螺线方法达到99%以上。

基于所构建的邻域像元集，对5种混合尺度的低空间分辨率像元值进行光谱分解，得出的部分高空间分辨率灰度图像如图9所示。可见，随着混合尺度增加，窗口型方法分解结果中越来越多像元值的误差超出了辨识不同地物类别的界限(试验中各地物类别最小光谱差值为0.1，绝对误差超出其一半即意味着难以提供准确的光谱信息)；螺线型方法分解效果较好。通过统计试验区分解灰度图像绝对误差的绝对值，显示螺线型方法均值处于[4.4×10-4,1.3×10-3],标准偏差处于[0.4,1.2]；窗口型方法相应指标分别为[3.1×10-3，131.9]和[5.3×10-2，1.2×105]，表明螺线型方法对分解结果精度提高作用显著。水体、湿地类型广泛地与其他类型地物交错分布且数量较少，造成邻域像元集构建及分解难度较大；人造地表类型分布相对集中，具有较规则的形状，对这些区域的混合像元构建邻域像元集及分解的难度较小；灌丛地类型零星分布于林地周围，易造成欠定问题，但由于面积较大，其对整体精度的影响适中。通过对比两种方法在5种混合尺度上构建邻域像元集及分解的精度可知，螺线型构建方法在处理多种地表类型、复杂的地类分布上具有优势。

图8 试验区主要地表覆盖类型总体欠定像元比例Fig.8 The whole underdetermined pixels ratio among class map

对每个混合像元及试验区总体图幅构建邻域像元集合与进行混合像元分解所需的时间如图10所示。结果表明，螺线型方法构建邻域像元集合所需时间是窗口型方法的1.63倍，基于其构建的邻域像元集合进行解混，所需时间是窗口型方法的2.16倍，其构建及分解效率均低于窗口型方法。

图9 部分分解灰度图像(分解值的绝对偏差大于0.05的像元标记为黑白方块)Fig.9 The grey unmixed images of the test area (unmixed pixels that absolute deviation of values greater than 0.05 are marked as black and white block)

4 结 论

利用线性光谱混合模型分解低空间分辨率的像元光谱值时，在部分地表区域会发生解算方程组欠定问题，解不出组分的光谱值。传统基于窗口的邻域像元集构建方式难以解决该问题，其原因在于：一是规则的矩形区域难以应对地表上多种地物分布形态，使该构建方式难以准确获得相似的像元；二是其构建过程缺少对像元组分类型的判别，其邻域像元集未达到线性方程解算要求。螺线作为一种非规则的几何曲线，其形态更加贴近非规则的地表。基于螺线栅格化形式的邻域像元集构建方法，在邻域内遍历到足够的相似像元时，可在异质性不同的各地表区域构建出空间邻近、组分相似的邻域像元集，即可组建非欠定的线性方程组。本质上，螺线与窗口方式均是通过逼近混合像元的邻域，来获取其周围像元组成邻域像元集，其区别在于用来逼近邻域地表的是面状的窗口还是线状的螺线。螺线以一种细粒度的方式对分布于邻域地表的像元进行由内而外，并顾及四周的顺序遍历方式，这是面状的窗口所不具备的。邻域像元多是以非规则的分布方式位于混合像元周围，因此，细粒度的螺线较粗粒度的规则窗口在拟合邻域地表方面更加灵活。通过结合对遍历的各像元进行取舍，构建的邻域像元集可极大地避免欠定问题，进而提高分解精度。

在北京区域GlobeLand 30地表覆盖数据上的试验表明，相较于传统窗口构建方法，螺线型构建方法将欠定像元比例减少了近两个数量级，从构建邻域像元集合方面可将总体理论精度提高2%；基于该方法的混合像元分解结果精度提高近一个数量级；其构建邻域像元集及进而分解所需时间约为原窗口构建方法的2倍。在本次试验中，所用螺线并未以不同旋转方向逼近实际的地表分类图，但应注意到，其在邻域上的旋转方式可能对构建及分解结果产生影响。同时，螺线型构建方法的作用主要是逼近地物在地表分布形式，当地表两种以上的地类仅存在于极少稀疏分布的混合像元中时，该方法仍难以成功构建邻域像元集；在其他地表覆盖数据产品和几何光学、概率等其他光谱混合模型中的应用效果还不明确，这些问题仍需深入研究。

[1] 陈军，陈晋，廖安平，等.全球30 m地表覆盖遥感制图的总体技术[J].测绘学报，2014，43(6)：551-557.DOI：10.13485/j.cnki.11-2089.2014.0089.

CHEN Jun，CHEN Jin，LIAO Anping，et al.Concepts and Key Techniques for 30 m Global Land Cover Mapping[J].Acta Geodaetica et Cartographica Sinica，2014，43(6)：551-557.DOI：10.13485/j.cnki.11-2089.2014.0089.

[2] CHEN Xuehong，YANG Dedi，CHEN Jin，et al.An Improved Automated Land Cover Updating Approach by Integrating with Downscaled NDVI Time Series Data[J].Remote Sensing Letters，2015，6(1)：29-38.

[3] CHEN Jun，CHEN Jin，LIAO Anping，et al.Global Land cover Mapping at 30 m Resolution：A POK-based Operational Approach[J].ISPRS Journal of Photogrammetry and Remote Sensing，2015，103(1)：7-27.

[4] GEVAERT C M，GARCíA-HARO F J.A Comparison of STARFM and an Unmixing-based Algorithm for Landsat and MODIS Data Fusion[J].Remote Sensing of Environment，2015，156(1)：34-44.

[5] GAO Feng，MASEK J，SCHWALLER M，et al.On the Blending of the Landsat and MODIS Surface Reflectance：Predicting Daily Landsat Surface Reflectance[J].IEEE Transactions on Geoscience and Remote Sensing，2006，44(8)：2207-2218.

[6] PERERA K，TSUCHIYA K.Experiment for Mapping Land Cover and It’s Change in Southeastern Sri Lanka Utilizing 250 m Resolution MODIS Imageries[J].Advances in Space Research，2009，43(9)：1349-1355.

[7] SAVTCHENKO A，OUZOUNOV D，AHMAD S，et al.Terra and Aqua MODIS Products Available from NASA GES DAAC[J].Advances in Space Research，2004，34(4)：710-714.

[8] 吴波，熊助国.基于光谱最佳尺度分割特征的高光谱混合像元分解[J].测绘学报，2012，41(2)：205-212.

WU Bo，XIONG Zhuguo.Unmixing of Hyperspectral Mixture Pixels Based on Spectral Multiscale Segemented Features[J].Acta Geodaetica et Cartographica Sinica，2012，41(2)：205-212.

[9] ASNER G P，WESSMAN C A，PRIVETTE J L.Unmixing the Directional Reflectances of AVHRR Sub-pixel Landcovers[J].IEEE Transactions on Geoscience and Remote Sensing，1997，35(4)：868-878.

[10] 李慧，张金区，曹阳，等.端元可变非线性混合像元分解模型[J].测绘学报，2016，45(1)：80-86.DOI：10.11947/j.AGCS.2016.20140520.

LI Hui，ZHANG Jinqu，CAO Yang，et al.Nonlinear Spectral Unmixing for Optimizing Per-pixel Endmember Sets[J].Acta Geodaetica et Cartographica Sinica，2016，45(1)：80-86.DOI：10.11947/j.AGCS.2016.20140520.

[11] 张良培，沈焕锋.遥感数据融合的进展与前瞻[J].遥感学报，2016，20(5)：1050-1061.

ZHANG Liangpei，SHEN Huanfeng.Progress and Future of Remote Sensing Data Fusion[J].Journal of Remote Sensing，2016，20(5)：1050-1061.

[12] 邬明权，王洁，牛铮，等.融合MODIS与Landsat数据生成高时间分辨率Landsat数据[J].红外与毫米波学报，2012，31(1)：80-84.

WU Mingquan，WANG Jie，NIU Zheng，et al.A Model for Spatial and Temporal Data Fusion[J].Journal of Infrared and Millimeter Waves，2012，31(1)：80-84.

[13] RAO Yuhan，ZHU Xiaolin，CHEN Jin，et al.An Improved Method for Producing High Spatial-resolution NDVI Time Series Datasets with Multi-temporal MODIS NDVI Data and Landsat TM/ETM+ Images[J].Remote Sensing，2015，7(6)：7865-7891.

[14] 陈晋，马磊，陈学泓，等.混合像元分解技术及其进展[J].遥感学报，2016，20(5)：1102-1109.

CHEN Jin，MA Lei，CHEN Xuehong，et al.Research Progress of Spectral Mixture Analysis[J].Journal of Remote Sensing，2016，20(5)：1102-1109.

[15] 何青，熊桢.基于邻域的混合象元解译[J].北方交通大学学报，1999，23(4)：118-121.

HE Qing，XIONG Zhen.Neighbor-field-based Mixed Pixel Interpretation[J].Journal of Northern Jiaotong University，1999，23(4)：118-121.

[16] ZHUKOV B，OERTEL D，LANZL F，et al.Unmixing-based Multisensor Multiresolution Image Fusion[J].IEEE Transactions on Geoscience and Remote Sensing，1999，37(3)：1212-1226.

[17] MASELLI F.Definition of Spatially Variable Spectral Endmembers by Locally Calibrated Multivariate Regression Analyses[J].Remote Sensing of Environment，2001，75(1)：29-38.

[18] BUSETTO L，MERONI M，COLOMBO R.Combining Medium and Coarse Spatial Resolution Satellite Data to Improve the Estimation of Sub-pixel NDVI Time Series[J].Remote Sensing of Environment，2008，112(1)：118-131.

[19] ZURITA-MILLA R，CLEVERS J G P W，SCHAEPMAN M E.Unmixing-based Landsat TM and MERIS FR Data Fusion[J].IEEE Geoscience and Remote Sensing Letters，2008，5(3)：453-457.

[20] 谢登峰，张锦水，孙佩军，等.结合像元分解和STARFM模型的遥感数据融合[J].遥感学报，2016，20(1)：62-72.

XIE Dengfeng，ZHANG Jinshui，SUN Peijun，et al.Remote Sensing Data Fusion by Combining STARFM and Downscaling Mixed Pixel Algorithm[J].Journal of Remote Sensing，2016，20(1)：62-72.

[21] 张建，李宗南，谢静.亚像元定位之邻域像元选取问题研究[J].华中师范大学学报(自然科学版)，2013，47(3)：404-409.

ZHANG Jian，LI Zongnan，XIE Jing.Research on Neighbor Pixels Choosing Issue of the Sub-pixel Mapping[J].Journal of Huazhong Normal University (Natural Sciences)，2013，47(3)：404-409.

[22] 王明华，杨继绪.阿基米德螺线的性质与应用[J].数学通报，1989(7)：11-12.

WANG Minghua，YANG Jixu.The Properties and Application of Archimedean Spiral[J].Bulletin des Sciences Mathematics，1989(7)：11-12.

[23] 姚建武.螺线与生物体上的拟螺线[J].科学，2004，56(4)：61-63.

YAO Jianwu.On Spiral and Organism Draft Spiral Research[J].Science，2004，56(4)：61-63.

[24] XU Mingming，ZHANG Liangpei，DU Bo.An Image-based Endmember Bundle Extraction Algorithm Using both Spatial and Spectral Information[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2015，8(6)：2607-2617.

[25] DU Bo，ZHANG Liangpei.A Discriminative Metric Learning Based Anomaly Detection Method[J].IEEE Transactions on Geoscience and Remote Sensing，2014，52(11)：6844-6857.

[26] DU Bo，ZHANG Liangpei.Target Detection Based on a Dynamic Subspace[J].Pattern Recognition，2014，47(1)：344-358.

A Spiral-based Construction of Adjacent Pixel Sets for Linear Spectral Unmixing

LIU Boyu1,2，CHEN Jun2，XING Huaqiao2,3，WU Hao2，ZHANG Jun2

1.College of Geo-exploration Science and Technology，Jilin University，Changchun 130026，China; 2.National Geomatics Center of China，Beijing 100830，China; 3.Geoscience and Surveying Engineering College，China University of Mining and Technology (Beijing)，Beijing 100083，China

The problem of spectral mixing in fragmented landscape prevents the potentiality of high temporal resolution image from land surface detail dynamic monitoring.The general way is unmixing the spectrum to components based on linear spectral mixing model，with the aid of neighborhood pixels and the least squares method.However，constructing the neighborhood pixel set by a window leads to the underdetermined problem in some areas.This paper analyses the cause of the problem，and introduces spiral to construct optimal neighborhood pixel set as a solution.Experiment on GlobeLand 30 shows that the spiral method has a good applicability for each land surface type.Compared with the traditional method，the overall accuracy can be enhanced by 2%，the accuracy of unmixed results can be improved by nearly one order of magnitude.

linear spectral unmixing; mixed pixel; adjacent pixel; spiral; window

The State Key Program of National Natural Science Foundation of China (No.41231172)

LIU Boyu(1987—)，male，PhD candidate，majors in spatio-temporal data fusion and land cover mapping.

刘博宇，陈军，邢华桥，等.面向线性光谱混合分解的邻域像元集螺线型构建方法[J].测绘学报，2017,46(11)：1841-1849.

10.11947/j.AGCS.2017.20170109.

LIU Boyu，CHEN Jun，XING Huaqiao，et al.A Spiral-based Construction of Adjacent Pixel Sets for Linear Spectral Unmixing[J].Acta Geodaetica et Cartographica Sinica,2017,46(11):1841-1849.DOI:10.11947/j.AGCS.2017.20170109.

P237

A

1001-1595(2017)11-1841-09

国家自然科学基金重点项目(41231172)

(责任编辑：丛树平)

2017-03-09

修回日期：2017-07-12

刘博宇(1987—)，男，博士生，研究方向为遥感时空数据融合与地表覆盖制图。

E-mail：liuby10@mails.jlu.edu.cn