过阻尼布朗棘轮的斯托克斯效率研究∗
吕明涛 延明月 艾保全 高天附 郑志刚
1)(沈阳师范大学物理科学与技术学院,沈阳 110034)2)(华南师范大学物理与电信工程学院,广州 510006)3)(华侨大学信息科学与工程学院,厦门 361021)
过阻尼布朗棘轮的斯托克斯效率研究∗
吕明涛1)延明月1)艾保全2)高天附1)†郑志刚3)
1)(沈阳师范大学物理科学与技术学院,沈阳 110034)2)(华南师范大学物理与电信工程学院,广州 510006)3)(华侨大学信息科学与工程学院,厦门 361021)
(2017年6月27日收到;2017年8月27日收到修改稿)
根据随机能量理论解析得到阻尼环境中布朗粒子的概率流和斯托克斯效率,并进一步研究布朗粒子的输运性能.详细讨论了空间的不对称性、外偏置力及外势结构等对棘轮定向输运的影响.研究发现,合适的外偏置力能使棘轮的定向输运达到最强.通过调节外势的不对称性可使棘轮中粒子的运动反向,当选择合适的空间不对称性时布朗粒子的反向输运可获得最强.此外,一定条件下合适的外势高度也能增强棘轮输运,且能使粒子克服黏滞阻力的斯托克斯效率达到最大.所得结论能够启发实验上设计合适的外势及外偏置来优化布朗棘轮的定向输运性能,并为生物纳米器件的研制提供一定的理论参考.
概率流,黏滞阻力,斯托克斯效率,输运性能
1 引 言
生命体内部的细胞活动中分子马达扮演了重要角色.由于马达能够把化学能直接转化为机械能,所以这一独特的能量转换形式对细胞内的物质输送至关重要.为了研究分子马达的定向输运,人们提出了各种模型[1],包括物理上简单的布朗棘轮模型[2−4].通过研究不同棘轮中布朗粒子的运动情况,不但能了解布朗棘轮产生定向输运的机制,找到其定向输运的最优条件,而且能够提高棘轮对输入到系统中能量的有效利用.
对于不同棘轮的研究,如何增强棘轮的定向输运一直广受学者的关注[4−7].早期研究中,如Bao等[8]发现了在黏滞阻力及双噪声环境下布朗粒子的定向输运可被优化,说明黏滞阻力在一定条件下能够增强布朗粒子的定向输运.同时,Ai等[9]根据Fick-Jacobs方程解析得到了二维通道中布朗粒子概率流的表达式,并讨论了棘轮热泵的性能.此外,我们早期也研究了不同时空不对称度下布朗马达的定向输运性能,发现通过改变外势的不对称性粒子的输运能够增强[10].此外,文献[11]最新研究发现,改变外力的变化频率能够增强粒子的概率流,且当棘轮输入合适的外力时棘轮的能量利用率能够获得提高.
随着棘轮定向输运问题的深入研究,如何有效利用棘轮系统的能量已引起人们的极大兴趣.Sekimoto等[12]首先根据随机能量理论提出了不同环境中棘轮能量的分析方法,并计算了三种不同情况下棘轮的输入、输出功.有趣的是,卓益忠等[8]研究发现通过外偏置力的作用,布朗马达的能量利用率能够得到提高.此外大量实验表明,布朗马达拖动负载做功时会降低棘轮系统的输入能[10].同时,实验结果还表明,生物体内仍存在一类没有拖动负载却能产生定向运动的生物分子马达,并且这类马达克服阻尼环境运动时的定向输运效率非常高[13].因此,研究无负载下马达的能量利用问题也至关重要.然而这种情况下,若仍采用传统热力学效率的研究方法分析马达的能量转化问题,该计算方法将失去其物理意义.因此,无负载条件下布朗粒子的定向输运效率问题目前仍是人们研究的热点.理论上,根据Wang的分析,无负载情况下布朗粒子克服黏滞阻力运动时的输运效率称为斯托克斯效率[14].目前关于斯托克斯效率虽有一定研究[11,14],但并不是十分深入.如文献[15]中研究了时空不对称势下棘轮的输运特性,并对棘轮的热力学效率和定向输运效率(斯托克斯效率)分别进行了讨论.此外也对耦合布朗粒子的能量转化问题做了初步探讨,发现在一定条件下耦合粒子拖动负载做功时的能量转化效率能够获得提高[10].同时文献[11]对摇摆棘轮中概率流和斯托克斯效率的随机行为进行了讨论.在上述棘轮效率的研究中,人们大都采用数值方法研究不同棘轮的定向输运及能量转换问题.然而关于斯托克斯效率的解析求解至今还不够深入.因此,本文进一步采用解析方法讨论棘轮势中布朗粒子的定向输运效率问题.
根据Sekimoto[12]随机能量理论,研究了黏滞阻力作用下布朗粒子的定向输运及斯托克斯效率问题[16−20].研究发现,在一定不对称性下随外偏置力振幅的变化粒子可产生反向运动,且存在合适的外力振幅使概率流达到最强.此外,本文还发现合适的外势结构能够使粒子克服黏滞环境时的定向输运效率达到最强.应用本文所得结论实验上可以启发人们设计合适的外势及外偏置来增强棘轮的定向输运性能.
2 模 型
本文研究了处在过阻尼环境下的布朗粒子在空间不对称周期势中的运动,同时粒子受周期外力以及热噪声的作用,其动力学行为可由如下过阻尼朗之万方程描述[21,22]:
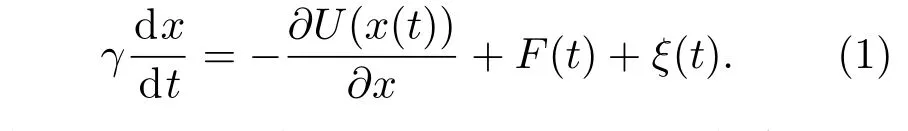
其中,x(t)表示粒子t时刻的位置,γ为介质阻尼系数,ξ(t)为高斯白噪声,且满足〈ξ(t)〉=0,〈ξi(t)ξj(t′)〉=2Dδijδ(t−t′), δ(t)是高斯噪声的关联函数,D表示噪声强度,F(t)为t时刻布朗粒子受到的非对称周期外力:
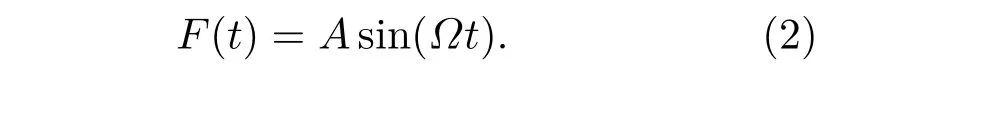
上式中A为外力振幅,2π/Ω为外力周期.此外,U(x)为周期外势,如图1所示,其表达式为

其中a为周期外势高度,L为外势的周期且满足U(x)=U(x+L),∆表示外势的不对称性,因此通过调节∆可改变外势的结构.
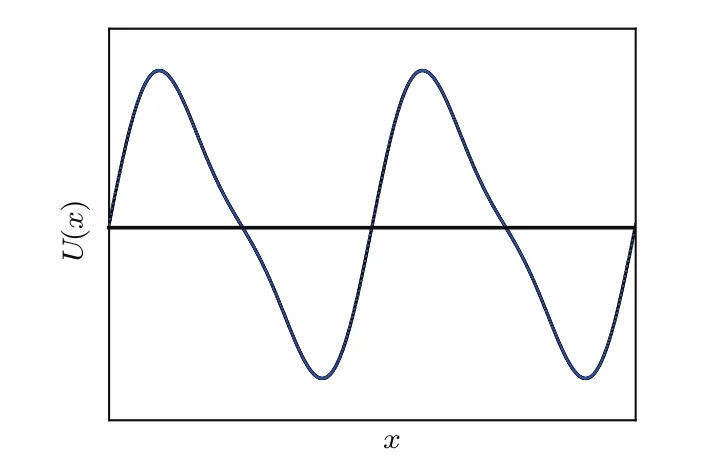
图1 外势U(x)的结构示意图Fig.1.The schematic diagram of U(x).
为讨论方便,令V′(x)=∂U(x)/∂x,根据文献[23]理论,与方程(1)对应的Fokker-Planck方程和概率密度流守恒方程为

其中kB是玻尔兹曼常数,T为热浴温度,且噪声强度D=kBT,P(x,t)表示在t时刻在位置x处的概率密度,并满足P(x,t)=P(x+L,t),j(x,t)为概率流,由上式可得:

如果F(t)变化很慢即系统为准静态,则
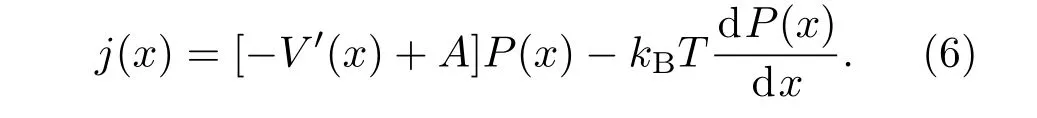
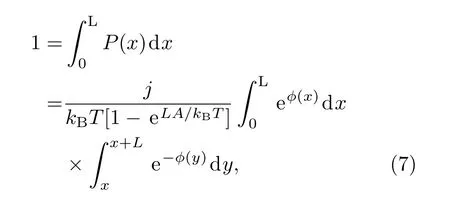
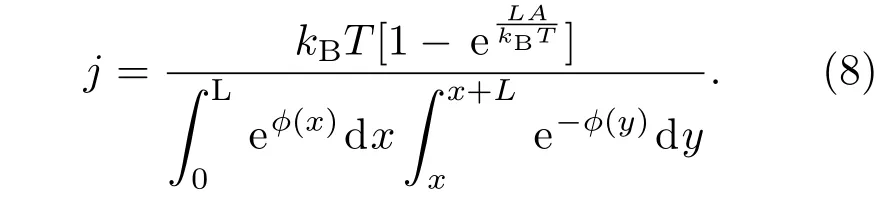
根据上式和已知条件可得系统概率流表达式:
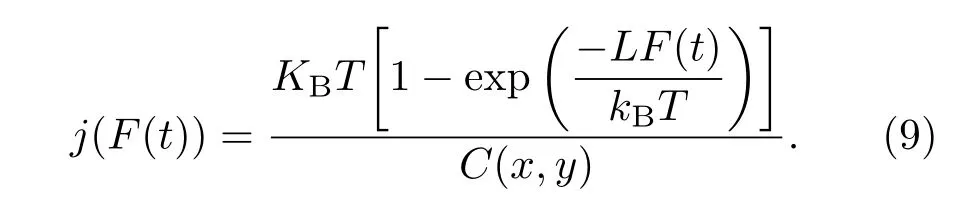
其中
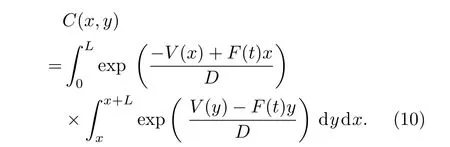
由于外力F(t)变化很慢,所以概率流也可表示为[23,25,26]
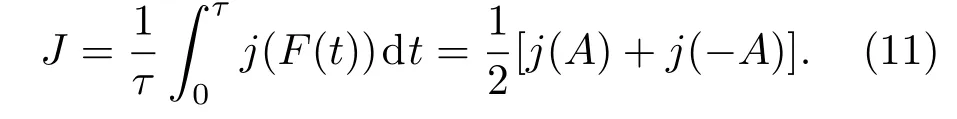
根据Sekimoto随机能量理论[12],释放到热浴中的能量为

其中ti和tf为积分始末时刻,且积分区间τ=ti−tf,单位时间内势能的变化为∆U,由能量守恒关系R=∆U+E,输入到系统中的总能量R可表述为
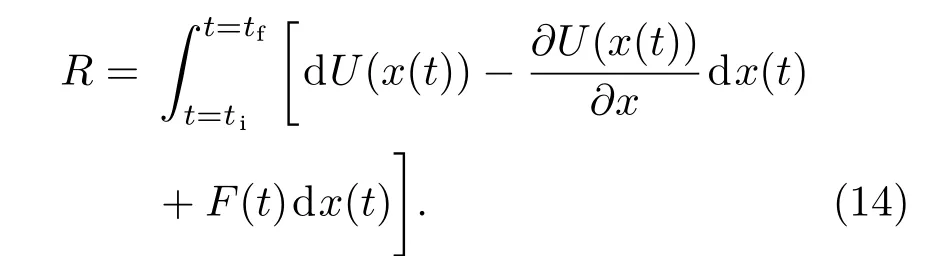
根据dU=(∂U/∂x)dx+(∂U/∂t)dt, 上式化简为[12]

由于外势的变化与时间t无关,∂U(x,t)/∂t=0,上式可写为[23,25]
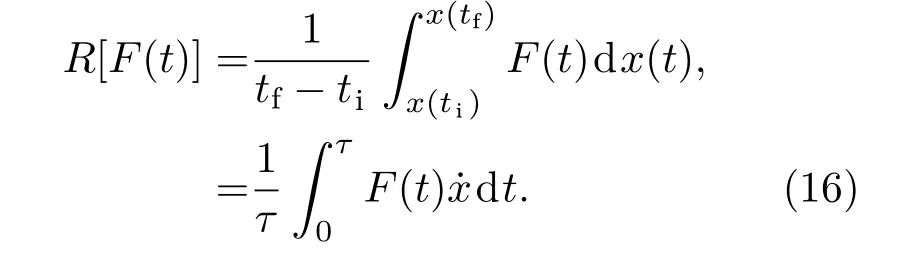
在准静态下,根据文献[24]理论,上式可进一步化简:

根据Mamata理论,斯托克斯效率定义为[11]

由(16)式可知输入到系统的能量:
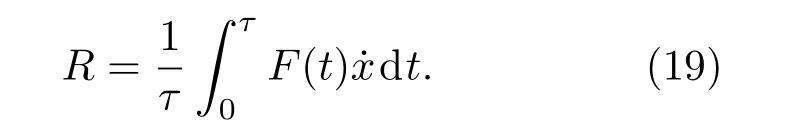
粒子克服阻尼力做功[15]:
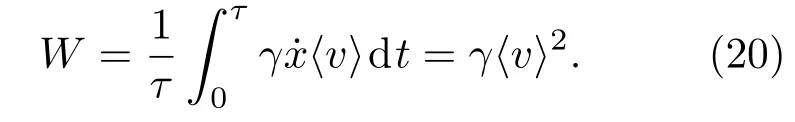
其中平均速度

所以斯托克斯效率的解析表达式为
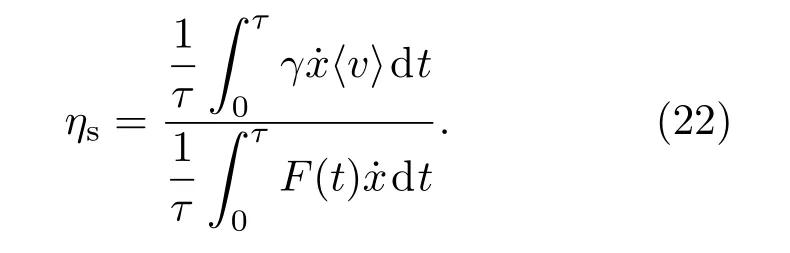
将(11),(17),(20)及(21)式代入(22)式可得:
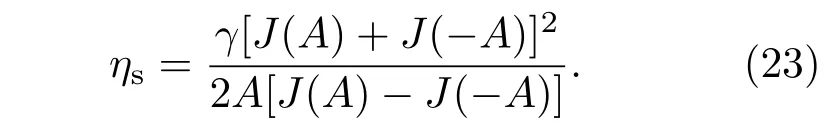
根据(11)及(23)式,本文主要研究阻尼环境中布朗棘轮的输运性能随系统各参量的变化关系,且所有物理量已采用无量纲化处理.如无特殊说明,文中参量取L=1.0,γ=1.0,D=0.01,∆=1.0,a=1/2π,A=1.0,Ω=2π.
3 结果与讨论
3.1 外力振幅A的影响
为了解棘轮的定向输运,研究了概率流随各参量的变化.首先讨论了当外势不对称度较小时,即∆=1.0时不同噪声强度下概率流J随外偏置力振幅A的变化关系,如图2(a)所示.当A较小时,概率流为负,且随A的增加棘轮产生的反向概率流逐渐增大.此时由于外偏置力振幅A较小,所以棘轮不容易产生定向输运.随着A的继续增加,反向概率流均存在峰值,该现象表明合适的外偏置力振幅能够促进棘轮的定向输运.当A继续增加时,|J|逐渐减小并趋于零.然而当A大于某一临界值且增大时,J>0,此时概率流与外偏置力呈类似正比关系,如图2(a)插图所示.说明此时外偏置力较大并占主导作用,因此粒子产生的定向输运更强.研究发现随噪声强度D的增加,概率流峰值逐渐减小,该现象表明较大的噪声并不利于粒子的定向输运.可见除外偏置力,噪声强度仍能影响粒子的定向输运.下文将深入讨论噪声强度对概率流的影响.
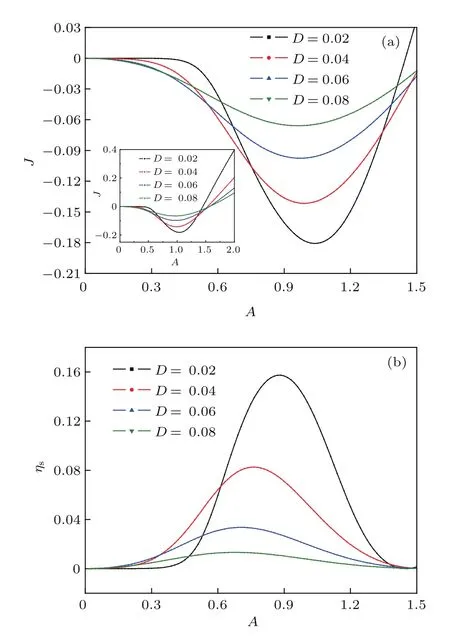
图2 (网刊彩色)∆=1.0时(a)概率流J和(b)斯托克斯效率ηs随外力振幅A的变化Fig.2.(color online)The curves of(a)particle flow J,(b)Stokes efficiency ηsvarying with the amplitude of external force A,where∆=1.0.
由(22)式分析可知,斯托克斯效率ηs反映了布朗粒子克服黏滞阻力产生定向输运的性能.因此本文研究了ηs随外偏置力振幅A的变化关系,如图2(b)所示.结果表明随着A的增加,不同噪声强度下的斯托克斯效率均逐渐增大且出现峰值.以D=0.02为例,发现在图2(a)和图2(b)中两组曲线的变化趋势类似.例如在A=1.0附近,反向概率流最大时相对应的斯托克斯效率也接近最大.根据(22)和(23)式可知,在一定条件下概率流越大,斯托克斯效率也越大,因此当过阻尼棘轮的定向输运达到最强时,相对应地粒子克服黏滞阻力的斯托克斯效率也会增强.此外研究还发现随D的增加ηs峰值也会减小,说明过大的热噪声不利于棘轮定向输运效率的提高,下文将继续讨论热噪声对棘轮输运性能的影响.
3.2 热浴环境中噪声强度D的影响
由于噪声强度对粒子输运有一定影响,研究了不同不对称度∆下概率流J随热噪声强度D的变化关系,如图3(a)所示.研究结果表明随D的增加,概率流也会小于零,说明在一定条件下热噪声可以使棘轮产生反向输运,该结论与文献[27,28]中所得结论类似,但产生机制并不完全相同.当D继续增加,棘轮存在合适的噪声强度使概率流达到最强.这一现象说明合适的热噪声也能增强棘轮的定向输运.随着D的进一步增大,|J|→0.说明当温度较高时,粒子在做自由扩散运动,所以此时棘轮不容易产生定向输运.有趣的是随不对称度∆的增大,反向概率流的峰值逐渐减小.该现象表明在一定条件下,较大的外势不对称度会抑制粒子的定向运动.通过(3)式分析,∆越大外势高度越大,因此粒子较难跨越势垒产生定向输运.由图2(a)可知,∆=1.0时,概率流可为负.为了深入研究粒子的输运方向问题,进一步研究了∆较小时,如∆=0.1,0.01时粒子的输运行为,如3(a)插图所示.研究发现,∆较小时概率流可为正,说明棘轮的定向输运对外势的不对称度有较强的敏感性,因此当∆较大时图3(a)中J-D会呈现反向概率流.因此该现象与文献[27]中噪声诱导棘轮产生流反转的机制并不完全相同.
如上述讨论,噪声强度能增强棘轮的定向输运.因此进一步研究了斯托克斯效率ηs随温度D的变化关系,如图3(b)所示.结果表明,在一定条件下存在合适的噪声强度使斯托克斯效率ηs达到最大.对照图3不难发现,J-D图像和ηs-D图像均出现峰值.这是因为合适的热噪声强度能够增强粒子输运并能提高棘轮的定向输运效率,所以布朗粒子克服黏滞阻力产生定向输运的性能也会获得提高.此外研究还发现随着外势不对称性的增大,斯托克斯效率的峰值逐渐减小.同样由(3)式可知这是由于∆越大,外势高度a越大,导致粒子不容易跨越外势产生定向运动.因此粒子克服黏滞阻力运动时的性能也被减弱.
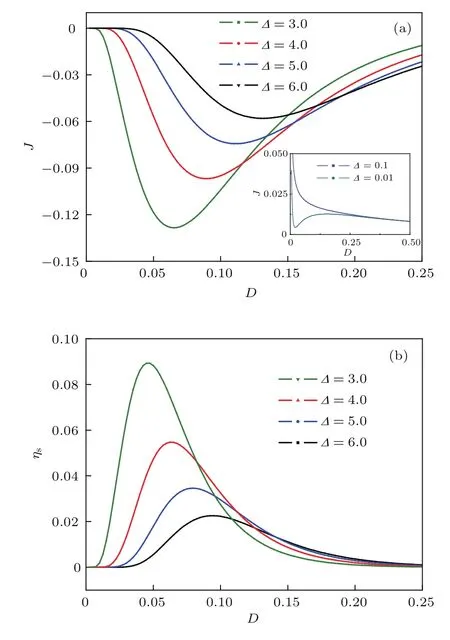
图3 (网刊彩色)A=1.0时(a)概率流J和(b)斯托克斯效率ηs随热噪声强度D的变化Fig.3.(color online)The curves of(a)particle flow J,(b)Stokes efficiency ηsvarying with the noise intensity D,where A=1.0.
3.3 外势不对称参数∆的影响
为了深入了解外势不对称性对棘轮输运性能的影响,本文研究了不同外力振幅下概率流J随外势不对称度∆的变化关系,如图4(a)所示.当∆较小时概率流为正且逐渐减小.当∆达到某一临界值时,即∆=∆c(如A=1.6),J=0.随着∆增加J<0且开始反向增大.当∆继续增大到另一临界值∆=∆m时,棘轮的反向输运最强.最终随着∆增加,|J|→0.产生上述输运现象主要是由于当外势不对称度∆<∆c时,∆越大,外势高度越大,粒子越难跨越外势产生正向输运;当∆>∆c时,概率流开始反向增加,这是由于随∆的继续增加,粒子将开始反向运动;有趣的是当∆=∆m时反向概率流最大,说明在一定条件下,合适的外势不对称性可增强粒子的定向输运;当∆>∆m时|J|→0,这是由于较大的外势不对称度占主导作用,导致粒子很难形成定向流.此外研究还发现,在一定∆范围内,J>0时的概率流与外偏置力振幅呈正比例变化,该结论与图2(a)中∆=1.0时的结论一致.因此只有在合适的外势不对称性和外偏置力共同作用下,棘轮的定向输运才能增强.
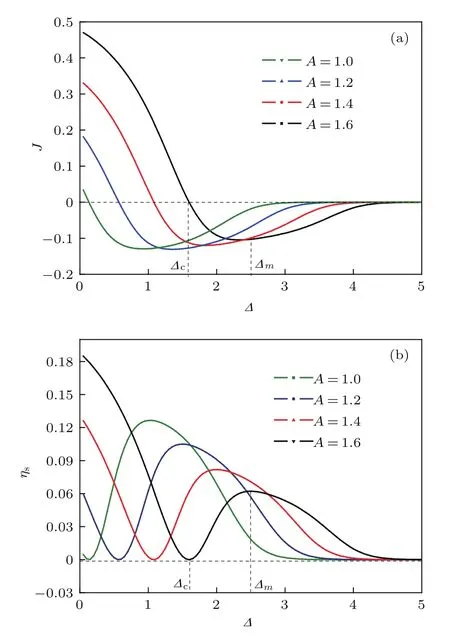
图4 (网刊彩色)D=0.01时(a)概率流J和(b)斯托克斯效率ηs随不对称参量∆的变化Fig.4.(color online)The curves of(a)particle flow J,(b)Stokes efficiency ηsvarying with the barrier asymmetric parameter∆,where D=0.01.
由于棘轮输运对外势不对称度有一定敏感性,讨论了斯托克斯效率ηs随外势不对称度∆的变化,如图4(b)所示.随∆的增加不同外偏置力振幅A下的ηs均逐渐减小,如A=1.6,当∆增加到某一临界值∆=∆c时,ηs→0.随∆继续增加,ηs开始逐渐增大,当外势的不对称度取某一合适值时,即∆=∆m,ηs达到峰值.研究发现,∆<∆c时ηs→0的现象主要是由于在图4(a)中相对应的J随不对称度的增加也逐渐减小,根据类似的讨论,由于ηs与概率流呈类似正比关系,所以ηs逐渐降低并趋于零;斯托克斯效率在∆=∆m处达到峰值说明合适的外势不对称度能够增强棘轮的定向输运性能;当∆>∆m,ηs逐渐减小并趋于零是由于外势的不对称度过大,外势过高,粒子更不容易产生定向运动,所以粒子克服阻尼力的定向输运效率减小并趋于零.此外研究还发现,ηs的峰值随外偏置力振幅的增大而减小,这一结论仍与图2(b)结论一致.
3.4 外势高度a的影响
由(3)式分析可知,外势不对称性可通过改变外势的高度影响粒子的定向输运.因此进一步研究了概率流随外势高度a的变化关系,如图5(a)所示.研究发现随a的增加概率流逐渐减小,当a达到某一临界值,a=ac时,J=0.当a继续增加J<0且反向增大,并在a=am处反向概率流达到峰值.最终随着a的增加,J→0.结果表明,以A=3.0为例,当a<ac时外势高度越小,粒子越容易跨越外势产生正向输运;当a>ac时J<0,说明当外势高度达到某一临界值后,粒子将反向输运;有趣的是概率流在a=am处达到峰值,说明外势高度仍存在一个合适值使粒子的输运达到最强;当a>am后概率流减小且|J|→0,这是由于外势过高,布朗粒子很难跨越外势产生定向输运.此外,随着外偏置力振幅A的增加,反向概率流的峰值也逐渐增大,说明一定条件下外偏置力越大,越促进粒子的定向运动,该结论与图2(a)中结论一致.因此,为了增强棘轮的定向输运,实验上可设计合适的外势结构及外偏置力使布朗粒子的定向输运达到最强[27].
由上述分析可知,外势高度能够影响粒子输运.因此进一步研究了不同外偏置力振幅下ηs随a的变化关系,如图5(b)所示.研究发现ηs随a的变化仍会出现极值,即在波峰a=am处和波谷a=ac处.结果表明,仍以A=3.0为例,a<ac时斯托克斯效率逐渐减小,说明一定条件下a越大粒子克服黏滞阻力的定向输运效率越低;当a>ac时ηs在a=am处出现峰值,说明合适的外势高度能促使粒子产生较强的定向输运,从而使粒子克服介质阻尼力的输运效率达到最强;然而当a>am时ηs逐渐减小并趋于零,该现象表明当外势较高时,粒子想要跨过外势形成定向输运的能力减小并逐渐消失.此外,研究还发现随外偏置力振幅的增加,粒子定向输运效率的峰值逐渐增大.该结论能够启发人们设计合适的外势结构来优化棘轮的定向输运性能.

图5 (网刊彩色)D=0.1时(a)概率流J和(b)斯托克斯效率随外势高度a的变化Fig.5.(color online)The curves of(a)Particle flow J,(b)Stokes efficiency ηsvarying with the barrier height a,where D=0.1.
4 结 论
研究了阻尼环境中处在时变外偏置力以及噪声作用下布朗棘轮的定向输运.深入分析了外势的空间不对称度、外偏置力振幅、外势高度及热噪声强度对棘轮定向输运的影响.研究结果表明,在合适的外势结构下,布朗粒子能够产生反向运动.同时存在合适的空间不对称度使概率流达到最强,并且当外偏置力振幅为某一合适值时,棘轮定向输运的能力能够获得提高.除此之外,合适的外势高度也能够使粒子克服黏滞阻力时的定向输运效率达到最强,从而有效地提高了棘轮的输运性能.本文所得结论不但能够启发人们设计不同类型的棘轮以增强粒子的定向输运并提高布朗粒子的输运效率,还可为医学上的药物输送及纳米器件的控制提供一定的理论指导作用[29−32].
[1]Xie P 2010Int.J.Biol.Sci.6 665
[2]Doering C R 1995Nuovo Cimento17 685
[3]Astumian R D,Bier M 1994Phys.Rev.Lett.72 1766
[4]Gao T F,Chen J C 2009J.Phys.A:Math.Theor.42 065002
[5]Ai B Q,He Y F,Zhong W R 2011Phys.Rev.E83 051106
[6]Zhang H W,Wen S T,Zhang H T,Li Y X,Chen G R 2012Chin.Phys.B21 078701
[7]Gao T F,Liu F S,Chen J C 2012Chin.Phys.B21 020502
[8]Zhan Y,Bao J D,Zhuo Y Z 1997Acta Phys.Sin.46 1880(in Chinese)[展永,包景东,卓益忠 1997物理学报461880]
[9]Ai B Q,He Y F,Li F G,Zhong W R 2013Phys.Rev.E138 154107
[10]Fan L M,Lü M T,Huang R Z,Gao T F,Zheng Z G 2017Acta Phys.Sin.66 010501(in Chinese)[范黎明,吕明涛,黄仁忠,高天附,郑志刚2017物理学报66 010501]
[11]Sahoo M,Jayannavar A M 2017Physica A465 40
[12]Sekimoto K 1997J.Phys.Soc.Jpn.66 1234
[13]Parrondo J M R,Cisneros B J D 2002Physics A75 179
[14]Wang H,Oster G 2002EPL57 134
[15]Li Y X,Wu X Z,Zhuo Y Z 2000Physica A286 147
[16]Chueshov I,Kuksin S 2008Physica D237 1352
[17]Winkler M,Abel M 2015Phys.Rev.E92 063002
[18]Anders M 2013Phys.Rev.E92 063002
[19]Sztuk E,Przekop R,Gradoń L 2012Chem.Process Eng.33 279
[20]Spiechowicz J,Luczka J,Machura L 2016Physics2016 054038
[21]Zheng Z G,Cross M C,Hu G 2002Phys.Rev.Lett.89 154102
[22]Li C P,Han Y R,Zhan Y,Hu J J,Zhang L G,Qu J 2013Acta Phys.Sin.62 230051(in Chinese)[李晨璞,韩英荣,展永,胡金江,张礼刚,曲蛟 2013物理学报 62 230051]
[23]Zeng C H,Wang H 2012Chin.Phys.B21 76
[24]Ai B Q 2004Ph.D.Dissertation(Guangzhou:Sun Yatsen University)(in Chinese)[艾保全 2004博士学位论文(广州:中山大学)]
[25]Kamegawa H,Hondou T,Takagi F 1998Phys.Rev.Lett.80 5251
[26]Ai B Q,Xie H Z,Liao H Y,Liu L G 2006J.Stat.Mech.50 09016
[27]Bartussek R,Hanggi P,Lindner B,Schimansky Geier L 1997Physica D109 17
[28]Kula J,Czernik T,Luczka J 1998Phys.Rev.Lett.80 1377
[29]Linke H 2002Appl.Phys.A:Mater.Sci.Process.75 167
[30]Heuvel MGLVD,Dekker C 2007Science317 333
[31]Braun O M,Kivshar Y S 1998Phys.Rep.306 1
[32]Landa P S,McClintock P V E 2000Phys.Rep.323 1
PACS:05.40.–a,05.40.Jc,02.30.Yy,02.50.–rDOI:10.7498/aps.66.220501
*Project supported by the National Natural Science Foundation of China(Grand Nos.11475022,11347003),the Scienti fic Research Funds of Huaqiao University,China and the Excellent Talents Program of Shenyang Normal University,China(Grand No.91400114005),and the Teaching Research Program of Thermodynamics and Statistical Physics in the Institution of Higher Education,China.
†Corresponding author.E-mail:tianfugao@synu.edu.cn
Stokes efficiency in the overdamped Brownian ratchet∗
Lü Ming-Tao1)Yan Ming-Yue1)Ai Bao-Quan2)Gao Tian-Fu1)†Zheng Zhi-Gang3)
1)(College of Physical Science and Technology,Shenyang Normal University,Shenyang 110034,China)2)(School of Physics and Telecommunication Engineering,South China Normal University,Guangzhou 510006,China)3)(College of Information Science and Engineering,Huaqiao University,Xiamen 361021,China)
27 June 2017;revised manuscript
27 August 2017)
Molecular motors in life activities of cell are known to operate efficiently.They could convert molecular-scale chemical energy into macroscopic-scale mechanical work with high efficiency.In order to acquire the transport mechanism of the molecular motor,the Brownian ratchet has been proposed to explore the property of directed transport and energy conversion.There are di ff erent kinds of Brownian ratchet models like flashing ratchets,rocking ratchets,and time-asymmetric ratchets and so on.Through investigating the performance of Brownian ratchet moving in periodic potential,the directed transport of ratchet could be explained,and the e ff ective usage of ratchet energy for directed transport could also be improved.Recently,optimizing the transport of Brownian ratchet has aroused the interest of researchers.It is found that the viscous resistance could reinforce the directed transport of the Brownian particle in damping liquid.Meanwhile,a large number of conclusions indicate that the transport of Brownian ratchets would be enhanced if the asymmetry of the potential is changed.Those results show that the in fluences of the external potential and the damping force on the particle flow cannot be neglected.Hence in this paper,the e ff ects of the potential structure and the temperature of heat bath on transport are discussed.
Furthermore,how to use the ratchet energy e ff ectively has been investigated in recent years.When the Brownian motor operates with load,the input energy is reduced.More importantly,the energy transformation efficiency de fined as the ratio of the useful work done against the load to the input energy is assumed to be a zero value in the absence of load.With the help of stochastic energetic theory proposed by Sekimoto,the Stokes efficiency has been used to explore the performance of the Brownian ratchet.So far,the numerical solution has been used extensively in most theoretical investigations.Nevertheless,in our work,the Stokes efficiency is discussed analytically for explaining the mechanism of directed transport.We consider the transport performance of the Brownian ratchet described by the Fokker Planck equation which is corresponding to the Langevin equation under time-varying external force and thermal noise.Mainly,the e ff ects of potential asymmetry,external force,height of the barrier,and intensity of the thermal noise on transport are discussed in detail.It is found that the transport direction of Brownian ratchet will be reversed under the condition of appropriate potential structures,and the probability current can reach a maximal value by changing the asymmetry of potential.It is worthwhile to point out that the performance of directed transport of the ratchet can be improved when an appropriate amplitude of the external force is applied.Meanwhile,there is an optimal value of the barrier height at which the Stokes efficiency reaches a maximal value and the directed transport of ratchet is enhanced.Through our conclusions,the ratchets of di ff erent structures could be designed for improving the transport property of Brownian motor.And the results have helpful theoretical guidance not only in the aspect of medical delivery but also in the control of nano-devices.
probability current,viscous resistance,Stokes efficiency,transport property
10.7498/aps.66.220501
∗国家自然科学基金(批准号:11475022,11347003)、华侨大学科研启动费项目和沈阳师范大学优秀人才支持计划 (批准号:91400114005)和高等学校热力学与统计物理课程教学研究项目资助的课题.
†通信作者.E-mail:tianfugao@synu.edu.cn

