圆环结构磁光光子晶体中的拓扑相变∗
沈清玮 徐林 蒋建华2)
1)(苏州大学物理与光电.能源学部,苏州 215006)2)(苏州大学,2011苏州纳米科技协同创新中心,苏州 215006)
圆环结构磁光光子晶体中的拓扑相变∗
沈清玮1)徐林1)蒋建华1)2)†
1)(苏州大学物理与光电.能源学部,苏州 215006)2)(苏州大学,2011苏州纳米科技协同创新中心,苏州 215006)
(2017年8月30日收到;2017年11月8日收到修改稿)
二维圆环结构的三角晶格磁光光子晶体中可以呈现多重拓扑相.在不同的几何参数和磁场下,这些拓扑相包括正常光子带隙相、量子自旋霍尔相和反常量子霍尔相.与文献[1]类似,该结果展现了二维光子晶体丰富的拓扑相变现象.
光子晶体,拓扑相变,拓扑边界态
1 引 言
1879年,美国物理学家Hall发现电流通过有垂直磁场的导体时会产生侧向电压,这一现象被称为霍尔效应[2].大约在100年后,也就是1980年,德国物理学家von Klitzing实验观测到在强磁场下,二维电子气的霍尔电导呈现出阶梯化的变化,被称为整数量子霍尔效应[3].1982年,Thouless等[4]指出这种整数化的霍尔效应是由于能带的非平庸拓扑性质导致的.根据他们的理论,量子霍尔效应中的整数对应一种被称为第一类陈数的拓扑量子数.1988年,Haldane提出了在周期交错的磁场下获得量子化电导的方法.由于该方法总的磁通量为零,因而被称为反常量子霍尔效应(quantum anomalous Hall e ff ect,QAH e ff ect)[5].反常量子霍尔效应通常用来指没有朗道能级图像的量子霍尔效应系统,特别是有磁性系统的量子霍尔效应[6].虽然这个办法不需要外加磁场,但是局域范围内体系的时间反演对称性是被破坏的(time-reversal broken,TRB).2005年和2006年,Kane和Mele[7],以及Zhang等[8]分别提出了受时间反演对称性保护的二维量子自旋霍尔效应(quantum spin Hall e ff ect,QSHE)和三维拓扑绝缘体.量子自旋霍尔效应和三维拓扑绝缘体由一种新的拓扑量子数描述,称为Z2拓扑数(有时可以表示为“自旋陈数”,实际上是第二类陈数).随后,在2011年拓扑晶体绝缘体[9]和Floquet拓扑绝缘体[10]相继被提出.
从量子霍尔效应和反常量子霍尔效应到量子自旋霍尔效应,体系的时间反演对称性质从无到有.在量子霍尔效应中,由于时间反演不对称,只有单向传输的手性边界态(chiral edge state).而在量子自旋霍尔效应中,由于电子是费米子,时间反演对称性保证了Kramers二重简并(自旋简并),从而导致了自旋反向的双向导通螺旋边界态(helical edge states):自旋上的电子朝一个方向运动,自旋下的电子朝相反的方向运动.如果在自旋量子霍尔效应中引入微小的时间反演不对称,原有的Kramers二重简并将会出现分裂,但只要体系的带隙不闭合,双向导通的边界态仍然存在.这样的体系可称之为时间反演破坏的量子自旋霍尔效应(TRB QSHE).如果进一步加大时间反演不对称性,体系将会发生拓扑相变,带隙会先闭合再打开,进入一个新的拓扑相,反常量子霍尔效应相(QAH).QAH相存在单向导通的边界态,所以拓扑相变的一个重要结果就是边界态性质的改变.通过改变时间反演对称性破坏的程度,体系可以经过QSHE到TRB QSHE,再到QAH的转变过程.
在光子晶体学领域中,光子能带的拓扑现象最早由Haldane和Raghu在2008年提出[11,12].他们在磁光光子晶体系统给出了实现光学的量子霍尔效应的方案.随后更多的光学的量子霍尔效应和单向边界态被人们广泛地研究并在实验上实现[13−15].由于光子属于玻色子,没有Kramers二重简并,无法直接将量子自旋霍尔效应和拓扑绝缘体的概念推广到光子晶体.虽然如此,但是人们还是通过其他对称性质加上玻色系统的时间反演对称构造了类似电子系统的赝时间反演对称和对应的赝自旋1/2态.这样的赝自旋1/2态有利用光子偏振特性的TE+TM/TE-TM混合模式[16,17]和TE/TM模式[18]实现的二重简并,也有利用空间对称性质的顺时针/逆时针能流态[19]构成的.因为时间反演对称操作在电子自旋1/2态的作用数学上等价于赝时间反演对称操作在赝自旋1/2态的作用,所以可以将电子的自旋量子霍尔效应的拓扑上的结论映射到光子晶体体系中来.与此同时,通过连续破坏时间反演对称性,也可以研究在光子体系中的拓扑相变的问题.
最近,Chen等[1]报道了在二维蜂窝状晶格磁光光子晶体中,通过调控原胞的几何结构和外加磁场破坏时间反演对称性质,可以实现光学中的自旋量子霍尔效应相到时间反演破坏的自旋量子霍尔效应相,再到反常量子霍尔效应的相变过程.本文研究了在二维圆环结构的磁光光子晶体中的拓扑相变问题.根据之前的工作[20]可知,无外磁场时,在三角晶格C6点群和真实的TR对称构造的赝TR对称的保护下,通过调节圆环内外径大小,可以实现二维光子晶体的自旋量子霍尔态或者普通的绝缘态.基于此,当逐渐增加外磁场时,由于磁光介质的法拉第效应,破坏了体系的时间反演对称,二维光子晶体将经历自旋量子霍尔效应到时间反演破坏的自旋量子霍尔效应,再到反常量子霍尔效应的相变过程.数值计算的能带和拓扑边界态证实了相变过程.本文的工作丰富了调控二维光子晶体的拓扑相变的方法.
2 光子晶体的结构和相变
考虑的二维光子晶体是圆环磁光材料摆成的三角晶格体系.如图1(a)所示,晶格常数为a,磁光材料的圆环内外半径分别为R1和R2.磁光材料为钇铁石榴石(YIG),它的介电常数是它的磁导率张量为.这个张量取决于外磁场和光子频率.它的取值由Drude模型决定[21],其中饱和磁化率4πMs=1884.通常在1600 Gauss的磁场和4.28 MHz下,YIG磁导率的张量元分别取κ=12.4u0和u=14u0.
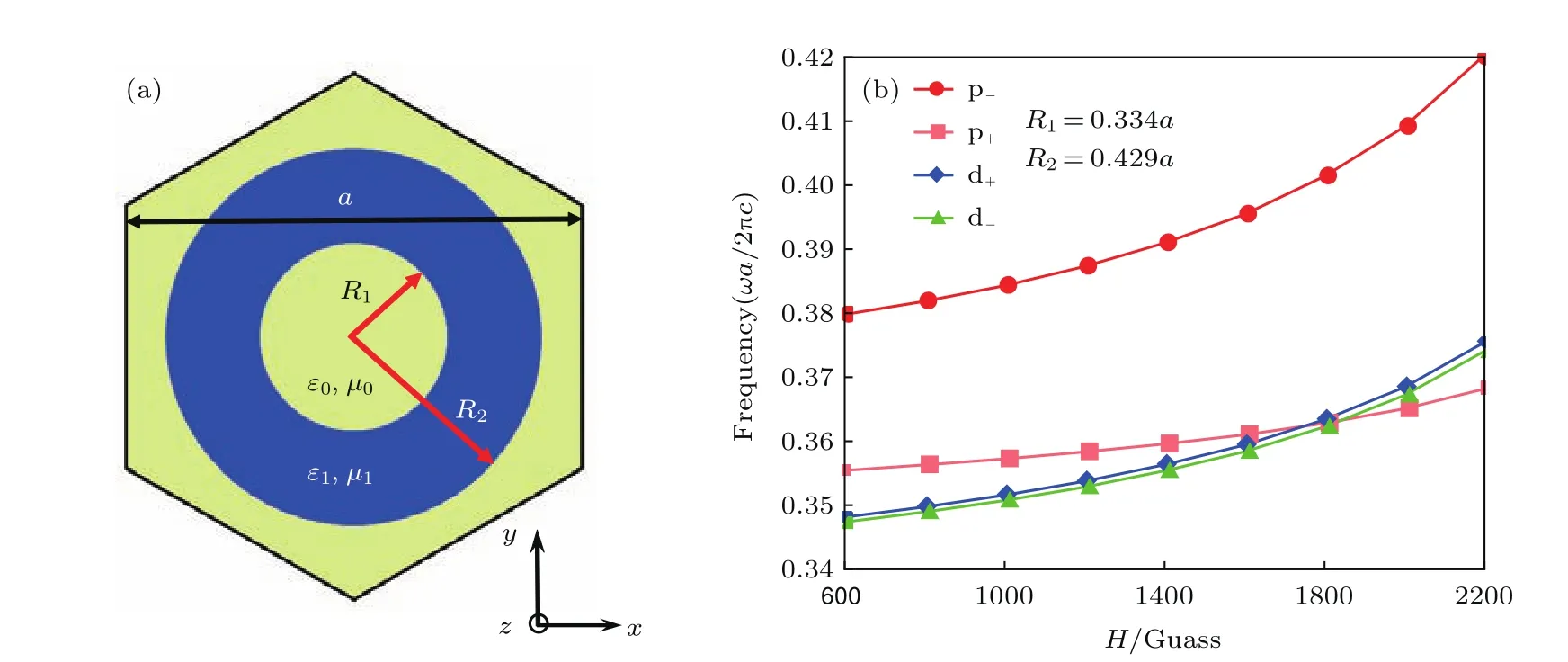
图1 二维光子晶体原胞结构示意图和能带相变图 (a)三角晶格晶格常数为a,背景是空气,介电常数和真空磁导率分别为ε0和µ0,圆环结构的内外半径R1和R2是可调控的;(b)在R1=0.334a和R2=0.429a(a=0.013 m)的原胞结构时,无外加磁场下,光子晶体是QSHE的相,随着外加磁场H的增大,体系发生了拓扑转变Fig.1.The structure of unit cell and phase transition of two dimensional photonic crystal:(a)Lattice constant is a,dielectric constant and permeability of vacuum is ε0and u0respectively,the radius of ring structure R1and R2are tunable;(b)When R1=0.334a and R2=0.429a(a=0.013 m)without external magnetic field,photonic crystal is in QSHE When external magnetic field is increasing,the topology of this system is changing.

图2 不同二维光子晶体能带 (a)在无外磁场、R1=0.005a和R2=0.388a的原胞结构A时,光子晶体在频率为0.46附近是普通的绝缘相;(b)在外磁场H=600,R1=0.357a和R2=0.450a的原胞结构B时,光子晶体在频率为0.46附近是时间反演破坏的自旋量子霍尔效应相;(c)在外磁场H=2200,R1=0.284a和R2=0.425a的原胞结构C时,光子晶体在频率为0.46附近是QAH相Fig.2.Di ff erent band structures in two dimensional photonic crystal:(a)When R1=0.005a and R2=0.388a without external magnetic field,photonic crystal is conventional insulator phase near the frequency of 0.46;(b)when R1=0.357a and R2=0.450a with external magnetic field H=600,photonic crystal is TRB a quantum spin Hall phase near the frequency of 0.46;(c)when R1=0.284a and R2=0.425a with external magnetic field H=2200,photonic crystal is QAH near the frequency of 0.46.
现在考虑横向磁场(TM)模式的光子晶体本征态问题.由于三角晶格具有C6对称性,所以光子晶体的能带在Γ点处存在两个二维不可约表示,分别为E1和E2[22].根据宇称的不同,E1的两个本征基态函数记为px和py,简并频率对应ω1;而E2的两个本征基态函数为记为dxy和dx2−y2,简并频率对应ω2.两个p态和d态可以分别构成两个赝自旋1/2态,即和对于普通的绝缘相而言,d态的频率高于p态.但是通过调节内外半径大小和材料的电介质参数,可以实现p态和d态的偶然简并,甚至能带的反转[20],这样就实现了光子的自旋量子霍尔相.如果普通的绝缘相和自旋量子霍尔相具有共同的带隙,那么在它们的边界上可以找到受体态拓扑性质保护的拓扑边界态.
加入外加磁场后,原来简并的赝自旋态的能级会劈裂.如图1(b)所示,在H=0时,光子晶体是自旋量子霍尔效应相,p态的频率高于d态.随着外加磁场的增加,体系变成时间反演破坏的自旋量子霍尔效应相.在H到达1700 Gauss时,体系变成了反常量子霍尔效应相.本文的能带结构和边界态是由商业软件COMSOL MULTPHYSICS计算的.考虑到所关心的能带频率处于10 GHz到14 GHz之间,对于有效的Drude参数,采取该频率段的平均值.晶格常数选取a=0.013 m来讨论能带结构的拓扑相变.
图2展现了3种不同拓扑相的能带图.其中A和B分别为普通的绝缘相和时间反演破坏的自旋量子霍尔效应相,它们在0.46附近有共同的带隙.体系C是QAH相.
3 拓扑边界态
图2所示的三种不同拓扑相A,B和C有共同的带隙.由于A和B的能带具有不同的陈数,根据拓扑能带理论中体态边界态的对应关系,如果A和C放在一起,将会在它们的边界上出现受拓扑性质保护的单向传输的手性边界态.我们用32个原胞构成长条状的超原胞,如图3(a),并计算得到该超原胞的投影能带图.在投影能带图中可以看出0.46频率点附近有表面态的色散关系.图3(b)和图3(c)分别展示了在s1和s2交面处ky=∓0.2π/a表面态的Ez的场分布.可以看出两者是同一种模式,只是在不同的交面而已,它们是单向传输的.因而单向传输的边界态的存在说明了A和B的能带陈数的不同.

图3 投影能带和陈数不同所导致的拓扑边界态 (a)计算由图2中A和C两种光子晶体各16个原胞构成的长条状的超原胞的投影能带,s1和s2为左右两个界面;(b)在能带P1点处,ky= −0.2π/a时,s1界面处拓扑边界态Ez的场分布;(c)在能带P2点处,ky=0.2π/a时,s2界面处拓扑边界态Ez的场分布Fig.3.Projected band structure and topological edge states induced by the di ff erence of Chern number:(a)Super cell consists of 16 unit cell A and 16 unit cell C of Fig.2.Projected band structure is calculated with two di ff erent interfaces s1and s2;(b)Ez field of topological edge state at interface s1of P1with ky= −0.2π/a;(c)Ez field of topological edge state at interface s2of P2with ky=0.2π/a.
类似地,由于A和B分别为普通的绝缘相和时间反演破坏的自旋量子霍尔效应相,因而它们的能带具有不同的Z2拓扑数.如果A和B放在一起,将会在它们的边界上出现受拓扑性质保护的一对螺旋边界态.我们用32个原胞构成长条状的超原胞,如图4(a),并计算得到该超原胞的投影能带图.在投影能带图中可以看出0.46频率点附近有表面态的色散关系.图4(b)和图4(c)分别展示了在s1交面处ky=∓0.2π/a表面态的Ez的场分布,构成该体系的一对螺旋边界态.通常该对螺旋边界态的能量是一样的,但是本文的体系中由于s1交面和s2交面并非完全等价,且在边界上的赝TR对称性被破坏,因而造成两个边界态的能量的不同.

图4 投影能带和Z2拓扑数不同所导致的拓扑边界态(a)计算由图2中A和B两种光子晶体各16个原胞构成的长条状的超原胞的投影能带,s1和s2为左右两个界面;(b)在能带P1点处,ky= −0.2π/a时,s1界面处拓扑边界态Ez的场分布;(c)在能带P2点处,ky=0.2π/a时,s1界面处拓扑边界态Ez的场分布Fig.4.Projected band structure and topological edge states induced by the di ff erence of Z2topological number:(a)Super cell consists of 16 unit cell A and 16 unit cell B of Fig.2.Projected band structure is calculated with two di ff erent interfaces s1and s2;(b)Ez field of topological edge state at interface s1of P1with ky= −0.2π/a;(c)Ez field of topological edge state at interface s1of P2with ky=0.2π/a.
4 结 论
利用磁光材料在三角晶格光子晶体中实现了多重拓扑相变.通过改变原胞的结构和外磁场的大小,三角晶格光子晶体可以具有正常光子带隙、量子自旋霍尔相和反常量子霍尔相,并且得到了手性边界态和螺旋边界态.本文空心圆环的结构比文献[1]的结构更为简单,因此为实现光子晶体的拓扑相变提供了更多的方法.
[1]Chen Z G,Mei J,Sun X C,Zhang X,Zhao J,Wu Y 2017Phys.Rev.A95 043827
[2]Hall E H 1879Am.J.Math.2 287
[3]Klitzing K,Dorda G,Pepper M 1980Phys.Rev.Lett.45 494
[4]Thouless D,Kohmoto M,Nightingale M,den Nijs M 1982Phys.Rev.Lett.49 405
[5]Haldane F D M 1988Phys.Rev.Lett.61 2015
[6]Xiao D,Chang M C,Niu Q 2010Rev.Mod.Phys.82 1959
[7]Kane C L,Mele E J 2005Phys.Rev.Lett.95 226801
[8]Bernevig B A,Hughes T L,Zhang S C 2006Science314 1757
[9]Fu L 2011Phys.Rev.Lett.106 106802
[10]Lindner N H,Refael G,Galitski V 2011Nat.Phys.7 490
[11]Haldane F,Raghu S 2008Phys.Rev.Lett.100 013904
[12]Raghu S,Haldane F 2008Phys.Rev.A.78 033834
[13]Lu L,Joannopoulos J D,Soljačić M 2014Nat.Photon.8 821
[14]Wang Z,Chong Y,Joannopoulos J,Soljačić M 2009Nature461 772
[15]Wang Z,Chong Y,Joannopoulos J D,Soljačić M 2008Phys.Rev.Lett.100 013905
[16]Chen W J,Jiang S J,Chen X D,Zhu B,Zhou L,Dong J W,Chan C 2014Nat.Commun.5 5782
[17]Khanikaev A B,Mousavi S H,Tse W K,Kargarian M,MacDonald A H,Shvets G 2013Nat.Mater.12 233
[18]Ma T,Khanikaev A B,Mousavi S H,Shvets G 2015Phys.Rev.Lett.114 127401
[19]Wu L H,Hu X 2015Phys.Rev.Lett.114 223901
[20]Xu L,Wang H X,Xu Y D,Chen H Y,Jiang J H 2016Opt.Express24 18059
[21]Pozar D M 2009Microwave Engineering(Hoboken:John Wileyamp;Sons)
[22]Sakoda K 2004Optical Properties of Photonic Crystals(Berlin:Springer Scienceamp;Business Media)
PACS:41.20.Jb,03.65.Vf,42.25.GyDOI:10.7498/aps.66.224102
*Project supported by the National Natural Science Foundation of China(Grant Nos.11675116)and the Faculty Startup Funding of Soochow University.
†Corresponding author.E-mail:jhjiang@hotmail.com
Topological phase transitions in core-shell gyromagnetic photonic crystal∗
Shen Qing-Wei1)Xu Lin1)Jiang Jian-Hua1)2)†
1)(Department of Physics,Optoelectronics and Energy,Soochow University,Suzhou 215006,China)2)(Collaborative Innovation Center of Suzhou Nano Science and Technology,Soochow University,Suzhou 215006,China)
30 August 2017;revised manuscript
8 November 2017)
We found that core-shell gyromagnetic photonic crystal of two-dimensional triangular lattice exhibit topological phases.In a certain parameters and magnetic field,those phases could be a conventional insulator phase,a quantum spin Hall phase,and a quantum anomalous Hall phase.Di ff erent from the structure of Ref[1],phase transitions in our core-shell structure does not involve changes of space symmetry,which depend on parameters of our structure and the broken of time reverse symmetry.Our result shows the variety of topological phase transitions in photonic crystals.
photonic crystal,topological phase transition,topological edge state
10.7498/aps.66.224102
∗国家自然科学基金(批准号:11675116)和苏州大学科研启动基金资助的课题.
†通信作者.E-mail:jhjiang@hotmail.com

