拓扑声子与声子霍尔效应∗
邢玉恒 徐锡方 张力发
(南京师范大学物理科学与技术学院,南京 210023)
拓扑声子与声子霍尔效应∗
邢玉恒 徐锡方 张力发†
(南京师范大学物理科学与技术学院,南京 210023)
(2017年9月28日收到;2017年11月6日收到修改稿)
拓扑学与物理的结合是近几十年物理学蓬勃发展的一个新领域,它不仅活跃在量子场理论以及高能物理中,更广泛地存在于凝聚态物理体系中,包括量子(反常、自旋)霍尔效应和拓扑绝缘体(超导体)等.声子是凝聚态体系中热输运的主要载体;最近由于各种声子器件的发现,声子学得到了广泛的关注.本文介绍了声子的拓扑性质以及声子的霍尔效应现象,分别评述了在破坏时间反演对称、破坏空间反演对称、以及同时破坏时间和空间反演对称三种情况下所产生的声子霍尔效应、声子谷霍尔效应等相关物理研究进展.最后对拓扑学在其他声学体系中的应用做了简单介绍,并进一步讨论了其未来的发展方向.
拓扑学,Berry相位,Berry曲率,声子霍尔效应
1 引 言
拓扑学是近代发展起来的一个数学分支,主要研究几何图形或空间在连续改变形状后还能保持不变的一些性质的学科.早在十七世纪科学家就提出了“位置几何学”和“相位分析”学说.1984年,英国布里斯托大学的科学家Michael Berry就提出了关于量子力学中的“几何相”概念[1],主要描述了当一个量子体系在参数空间沿着闭合路径缓慢变化时,系统本征态所发生的变化,即系统的哈密顿量在参数空间发生绝热演化时体系的本征态的变化.Berry相在拓扑物理学领域是一个重要的概念[2],Berry曲率由于揭示了量子力学中绝热过程的奥秘且最近因其在量子计算机的实现中的重要用途而引起了科学家们的广泛兴趣[3].Berry曲率最早出现在带有布洛赫电子的单带的动力学中,在应用于量子霍尔体系时,其半经典理论可以解释霍尔电流和量子霍尔电导率[4].近几年来,Berry相效应在解决铁磁材料中的反常霍尔效应时起到了重要的作用[5,6],这也使Berry曲率在拓扑材料应用中的研究得到科学家们的广泛关注.由于在拓扑物理方面原创性的贡献,Thouless,Haldane和Kosterlitz被授予2016年诺贝尔物理学奖.拓扑和物理的巧妙结合,带动了凝聚态物理的快速发展,比较有代表性的就是其近十年来逐渐兴起的一个分支——拓扑绝缘体[7,8],即在绝缘体中带隙中存在拓扑保护的边界态.
由于热二极管、热晶体管、热逻辑门等[9−11]的相继提出,最近几十年我们见证了声子学的飞速发展,从而使得利用声子进行热流控制和信息处理成为可能.由于声子作为一种中性的准粒子不能像电子一样可以通过洛伦兹力直接和磁场耦合,因此当Rikken等[12]科学家在顺磁介质样品中发现声子霍尔效应现象时,物理学家们普遍感到很惊奇,即在有热流通过的样品薄膜的垂直方向上施加磁场时可以观察到横向热流,由于电子对热流贡献可以忽略,所以把这种现象称之为声子霍尔效应.此实验被Inyushkin和Taldenkov[13]所重复.从那以后,科学家们提出了几种理论来解释这一现象[14].对于各种量子、自旋或反常霍尔效应的电子输运性质,拓扑理论已经成功地解释了一些潜在的机理,那么对于声子的输运性质是否也可以运用拓扑理论来进行研究呢?
2010年,Zhang等[15]将声子的霍尔热导率和声子谱的Berry曲率联系起来,揭示了声子的拓扑性质,并发现了其中的拓扑相变,从而开创了拓扑声子学的研究.其后,在2012年,Qin等[16]从能量磁化的角度对声子霍尔热导提出了修正.当磁场作用在具有自旋声子相互作用的体系上时,时间反演对称性会发生破缺,从而产生声子霍尔效应.在非磁性体系中,空间反演对称破缺而时间反演对称性得到保护,可以观察到谷声子霍尔效应[17].在2016年,Zhang研究组又继续通过半经典波包动力学方法统一研究了电子、声子、磁子等热霍尔效应,并得出了霍尔热导率在拓扑理论框架下的通用公式[18].最近Liu等[19]研究了时间反演对称性和空间反演对称性同时破缺的体系中的拓扑声子输运现象.
本文以Berry曲率为切入点,着重讨论Berry相以及Berry曲率的基本理论与性质.通过研究在单独破坏时间反演对称、破坏空间反演对称以及同时破坏时间反演对称和空间反演对称的声子体系中Berry曲率的变化对声子输运的影响.在本文的第二部分介绍了Berry相的基本理论知识,了解Berry曲率与拓扑结构之间的关系;第三部分介绍了破坏时间反演对称时所产生的声子霍尔效应,研究其中的Berry曲率对拓扑结构性质的一些影响;第四部分介绍了破坏空间反演对称后形成的声子谷霍尔效应;第五部分主要介绍同时破坏时间和空间反演对称时对拓扑结构的影响;第六部分简单介绍了Berry相效应在其他声学体系中的应用;第七部分对拓扑声子学的应用做了简单展望.
2 Berry相及拓扑结构
Berry相位由三个至关重要的部分构成,这三个关键的特性决定了其在拓扑学中的重要地位.第一,Berry相位是规范不变的,其本征波函数由线性齐次方程定义,这个性质使得Berry相位更加的物理化,早期的实验研究也是通过这个性质进行的.第二,Berry相位具有独特的几何性质,Berry相可以表示为在闭合参数空间的线性积分,且与实际路径的变化率无关,Berry曲率的这种独特的性质使得其得到了广泛的应用.第三,Berry相位与规范场论和微分几何有着密切的联系,这使得Berry相成为一种直观且意义十分重大的物理概念,尤其在今天的霍尔效应以及拓扑物理学的研究中具有重要的意义[7].
2.1 绝热循环演化
波函数的整体相位不会对物理观测造成影响,然而量子态之间的相对相位与很多的物理现象有关系.1984年,英国布里斯托大学的科学家Michael Berry提出了关于量子力学中的“几何相”概念,为了更好地诠释这个相位的物理意义,以下对这个相位进行简单的推导.
当物理系统沿着参数空间中任意闭合回路做绝热演化,其非简并本征态的变化除了一个额定的相位之外,必然回到其本身,该相位就称为Berry相位.设体系的哈密顿量算符是一组参量的R(R1,R2,···,RD)函数:

而R随着时间做周期性变化
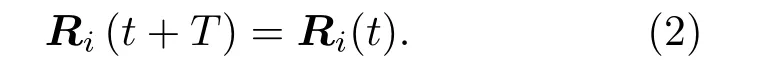
R(t)的周期变化在参量空间定义了一条闭合曲线C,假设此时周期T足够大,以致哈密顿算符随时间的变化非常缓慢,从而使得这一过程被称为绝热演化过程,致使系统在每一瞬间都是静止的.于是,对于某一瞬时t,瞬时定态薛定谔方程成立.在绝热条件下,瞬时本征波函数的含时薛定谔方程为
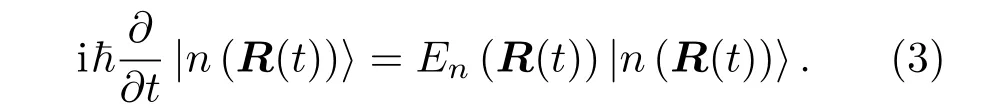
乘以〈m(R(t))|化简后得
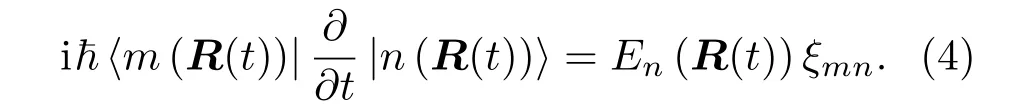
考虑一般含时薛定谔方程
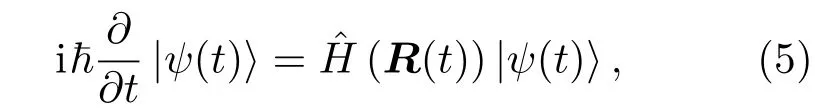
在绝热近似条件下,将本征函数归一化条件求导可得
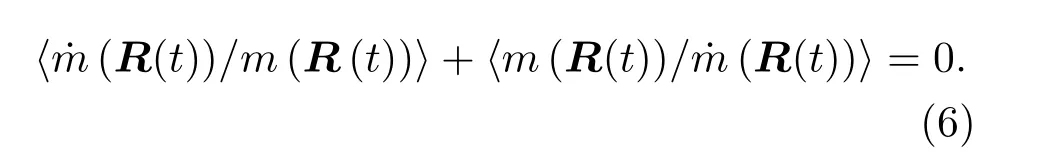
所以绝热近似下式含时薛定谔方程的解为
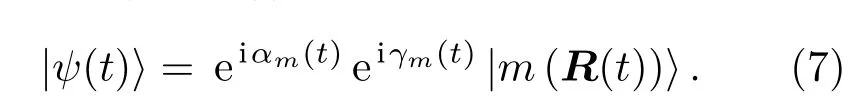
在引入R(t)的空间“矢势”后,Berry相位可以写成

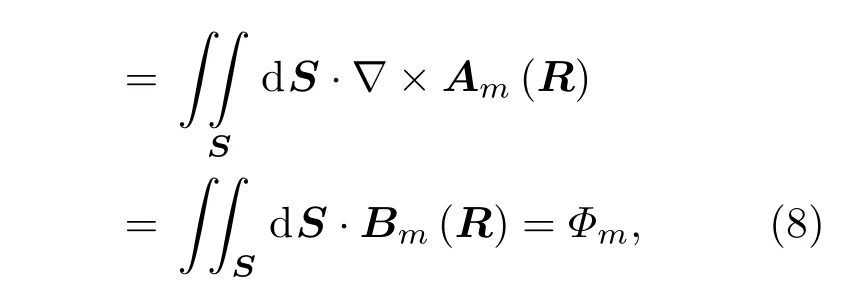
其中Bm(R)=∇R×Am(R)称为参数空间的“磁场强度”.
从上式可以看到:第一,Berry相位γm是实量;第二,Berry相位是一个规范不变的量,即在物理上是一个可以观测的量;第三,Berry相位不依赖于系统参数演化的快慢,只与演化的路径有关;第四,对于一维的参数空间,Berry相位为零,但是对于高维的参数空间,Berry相位不为零;第五,Berry相位是不可积的,也就是说它不能写成一个关于参数R的连续函数[20].故Berry相位仅与闭合回路或者闭合曲面的几何性质有关,与参数随时间的变化率无关,因此,Berry相位又称为几何相位.
2.2 Berry曲率
通过(8)式以及下面恒等式:
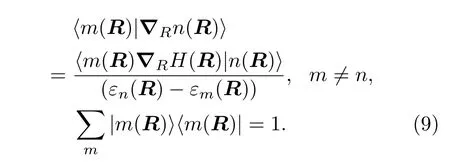
所以Berry曲率可以写成本征态的求和[21]:
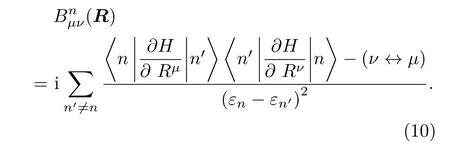
在这里,通常将A称为Berry联络(Berry connection),将B称为Berry曲率(Berry curvature).
在上述的公式推导过程中,最重要的就是绝热假设,即参数变化的足够缓慢从而使体系一直约束在某个能级上.也就是说此时的取值空间已经从整个完备的希尔伯特空间投影到某一个特定的能级上,这就是产生Berry相位的本质.
2.3 Berry曲率与对称性的关系
上述已经写出的Berry曲率的表达式
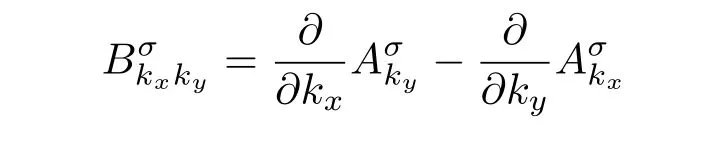
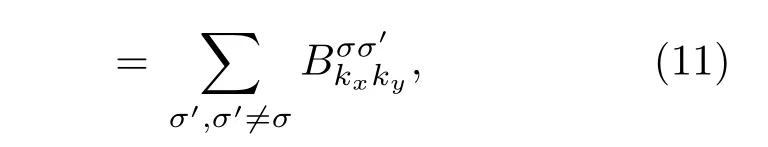
满足时间反演对称时
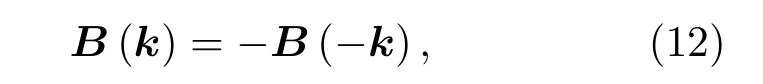
满足空间反演对称时
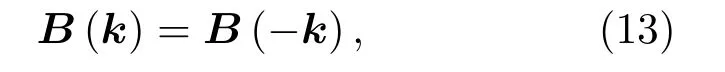
若同时满足空间和时间反演对称

2.4 布洛赫能带中的Berry相位
以上介绍了用哈密顿算子描述通用体系Berry相位的基本概念,现在考虑它在晶体中的实现.我们知道,晶体的能带结构为研究Berry相效应提供了一个天然的平台.在孤立电子近似下,首先可以写出单电子情况下的哈密顿量:
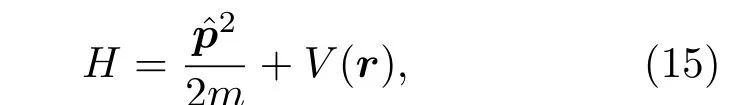
其中V(r+a)=V(r),a是布拉伐晶格的格矢,通过布洛赫定理,周期性的哈密顿量的本征态满足以下条件:
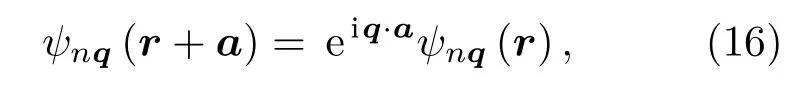
这里n是能带的数目,ħq是晶体的动量,通过进一步变换可得
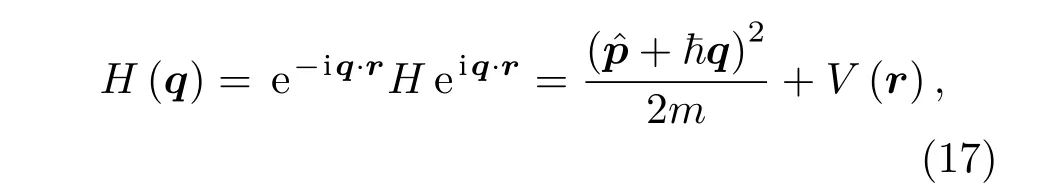
在这里,unq(r)=e−iq·rψnq(r) 是布洛赫函数的周期性部分,满足严格的周期性边界条件unq(r+a)=unq(r).Berry相位以及Berry曲率可以写成:
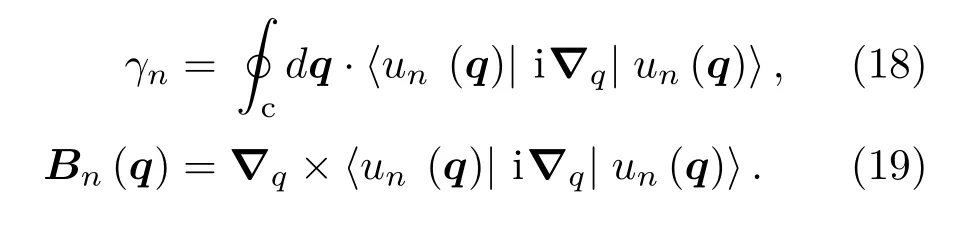
3 声子霍尔效应
3.1 霍尔效应的发现
霍尔效应是电磁效应的一种,这一现象是美国物理学家霍尔于1879年在研究金属的导电机理时发现的:即当电流垂直于外磁场通过导体时,载流子发生偏转,在垂直于电流和磁场的方向会产生一附加电场,从而在导体的两端产生电势差,这个电势差也被称为霍尔电势差.
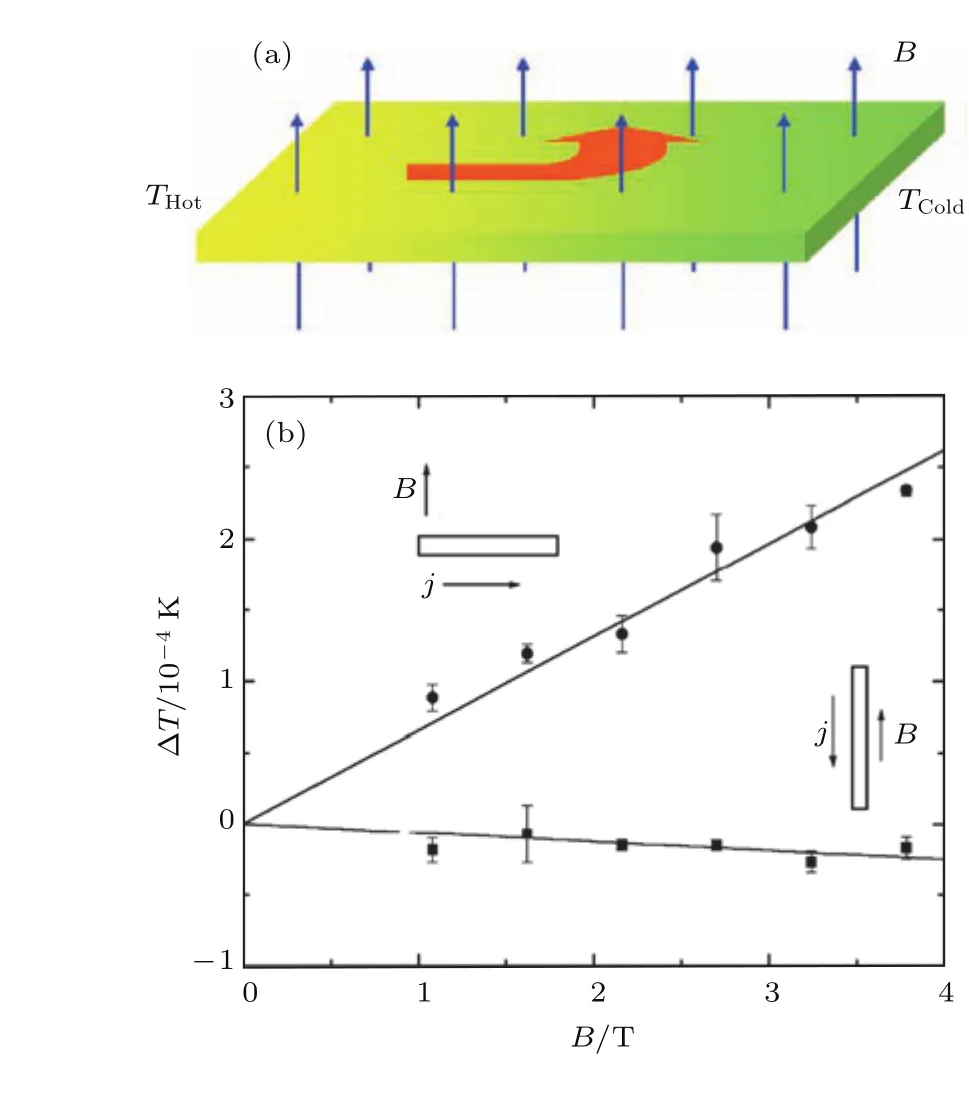
图1 (a)声子霍尔效应示意图,热流方向在磁场作用下发生偏转[24];(b)在Tb3Ga5O12薄膜样品测得的横向温差随磁场大小和方向的变化关系[12]Fig.1.(a)Phonon Hall e ff ect:the direction of the heat flow is de flected by the magnetic field[24];(b)magnetotransverse temperature di ff erence in a nonoriented sample of Tb3Ga5O15for heat currents perpendicular(circles)and parallel to the field(squares)[12].
近些年来,半导体材料和低维物理学的发展推动了许多霍尔效应的发展.在电绝缘的晶体中,声子是热流的载体,由于声子不能直接和磁场相互作用,所以通常认为不存在声子霍尔效应.最近,Strohm等[12]在顺磁介质Tb3Ga5O12薄膜样品中发现了声子霍尔效应现象,如图1所示,即在有纵向温度梯度的顺磁绝缘体薄膜上,加上垂直于薄膜平面的磁场后,测得横向温度差.当磁场方向平行于纵向热流时,横向温度差可以忽略,然而当磁场方向垂直于纵向热流(纵向温差为1 K)时,可以观察到200µK的温度差.由于电子不参与热输运,所以Strohm等将之命名为声子霍尔效应.此后该实验并被Inyushkin和Taldenkov[13]所重复.科学家们试图提出几种理论来解释这一现象[14,22],但是相对复杂并且有相互矛盾之处.另外,文献[23]利用非平衡态格林函数方法研究了具有自旋声子相互作用的四终端的二维薄膜的声子霍尔温差,从另一角度解释了声子霍尔效应.Zhang等[15]的工作从拓扑特性的角度首次对对声子霍尔效应进行了揭示,下面首先从声子霍尔体系的哈密顿量讲起.
3.2 哈密顿量以及二次量子化
在有磁场存在的情况下[14],离子晶体中晶格格点的动能可以写成
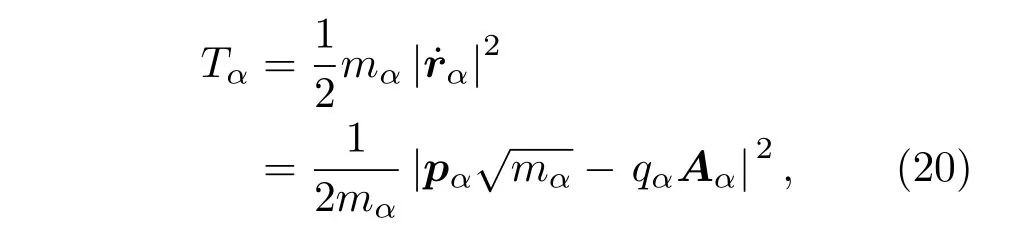
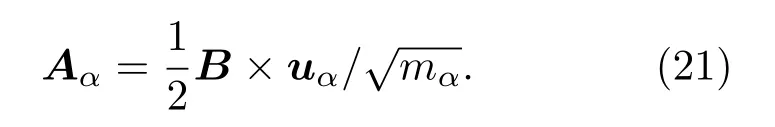
所以,上式可以写成
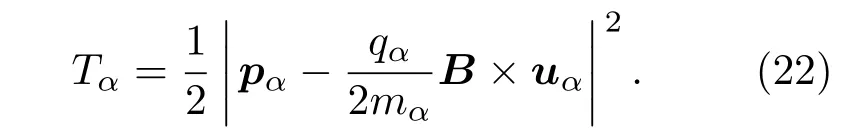
如果此时沿z方向施加强度为B的磁场,前提是只考虑二维情况下的运动(即只沿x和y方向),此时离子α的动能可以写成:
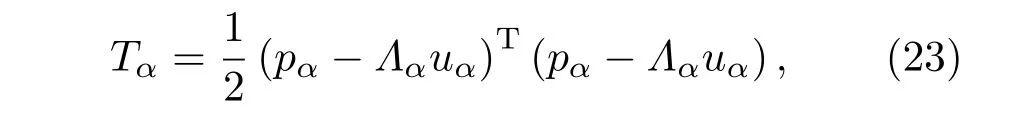
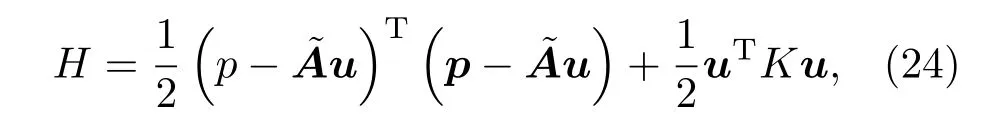
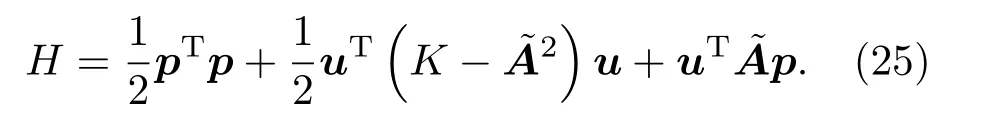
之前的理论中,科学家们考虑到拉曼相互作用的影响,基于量子理论和基本对称性的自旋-声子相互作用[26−28],得到了HI=h.(u×p),这里h=gcM,M与磁场B成正比.如果磁场沿z方向的作用,此时自旋-声子相互作用可以写成所以整个晶格的哈密顿量可以写成[29]
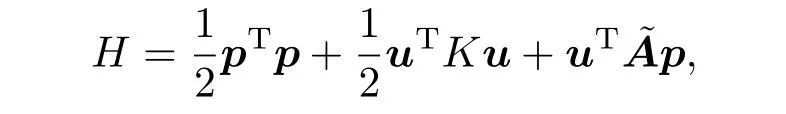
这和(25)式类似.然而此哈密顿量并不总是正定的,我们应该选用(25)式,其始终是正定的.
哈密顿量是关于u和p二次型方程,可以写出线性运动方程:
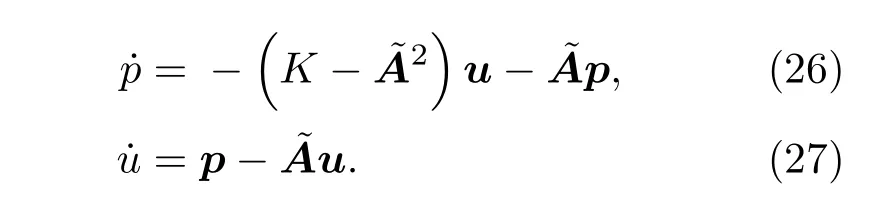
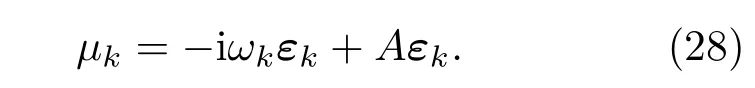
上式并不是标准的本征值问题,重新定义一个新的向量x=(µ,ε)T.然后,通过布洛赫定理,(28)式可以写成[15]:
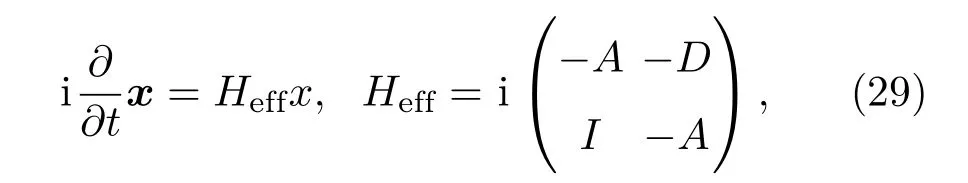
I是单位矩阵.因此,上式的本征值问题可以写成
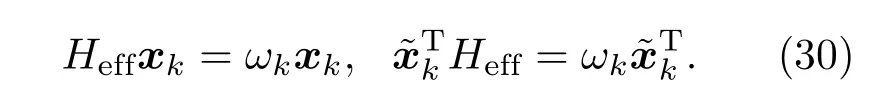
在这里,由于该有效哈密顿量是非厄米的,需要计(算右本征矢量为xk和左本征矢量对于本征矢εk的归一化条件即为
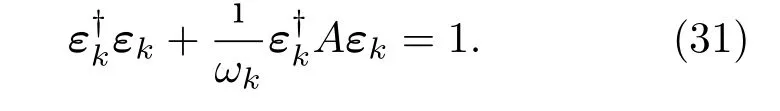
对于上式中的本征值问题,可知完备基包括负的分支等.从声子霍尔效应的拓扑性质可知[15],声子霍尔热导率的公式可以写成包括正负频的所有分支的贡献形式,为了简化符号,对于所有的分支,定义含时算子变换为变换关系为故由以上可以得到[15]:
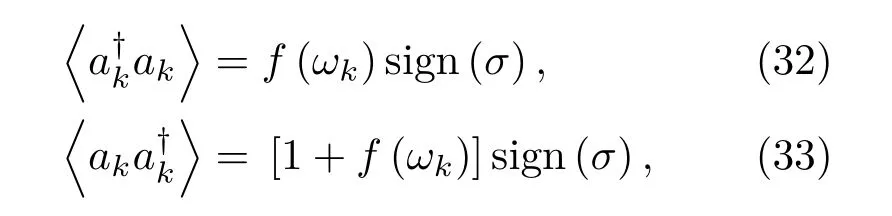
这里的f(ωk)为玻色-爱因斯坦分布方程.
在上述变化后,位移和动量运算符可以用二次量子化算符写成[30]:
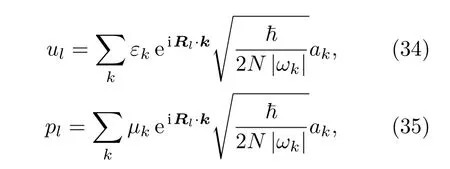
这里|ωk|=ωksign(σ).通过上述,系统的哈密顿量可以写成
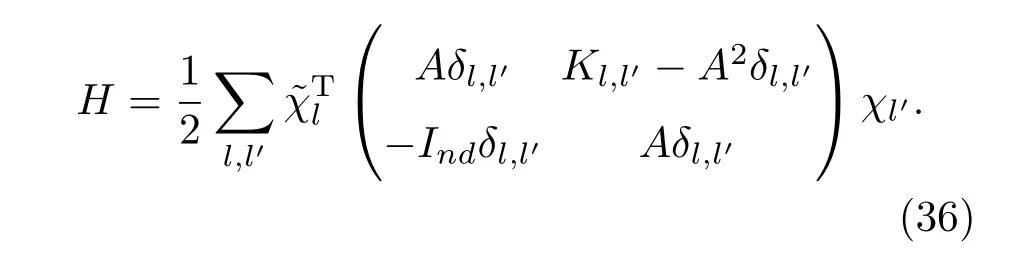
通过一系列变换后,哈密顿量最终可以化为[30]
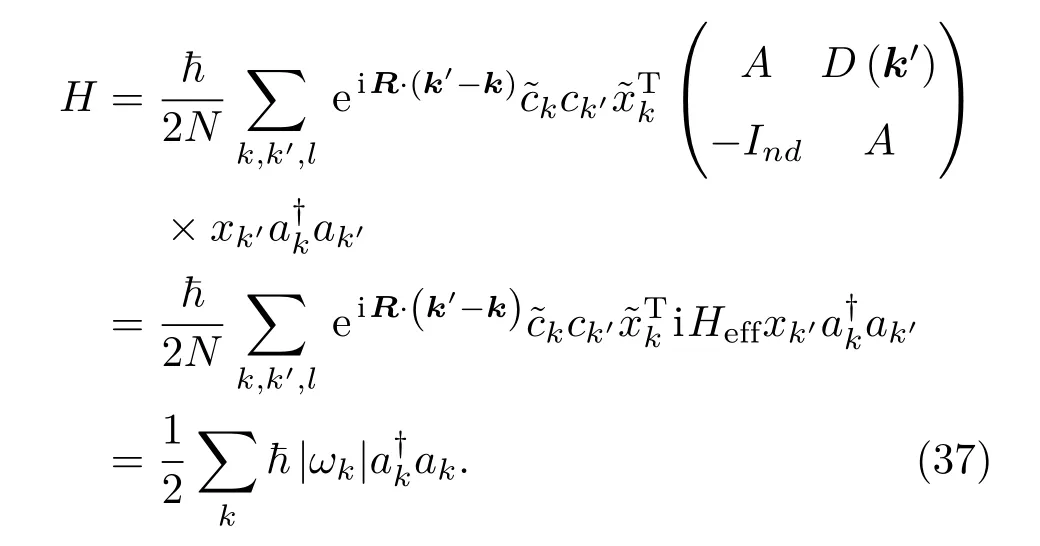
系统的热流可以写为[30]
这里V是N个基本原胞的总体积.通过对上述式的求导并引入Berry联络得出最终的热流公式:
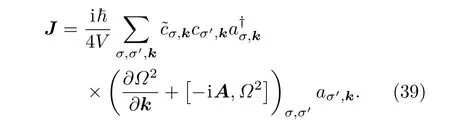
通过格林-库珀公式,可以计算得到霍尔热导线性响应贡献κKubo:
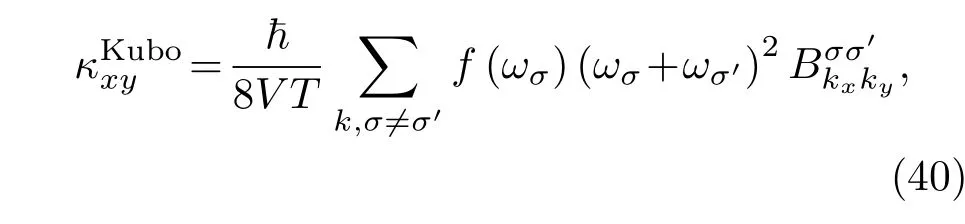
其中:
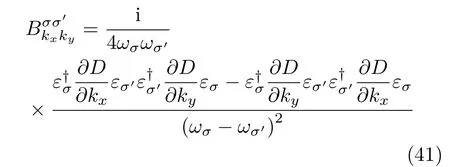
是σ带到σ′带的对Berry曲率的贡献.另外我们还必须考虑能量磁化贡献ME[16],总的霍尔热导率可以写为
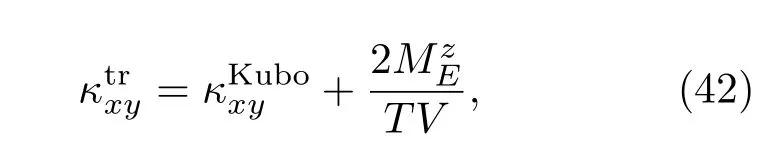
最终可以得到声子热导率公式[16]
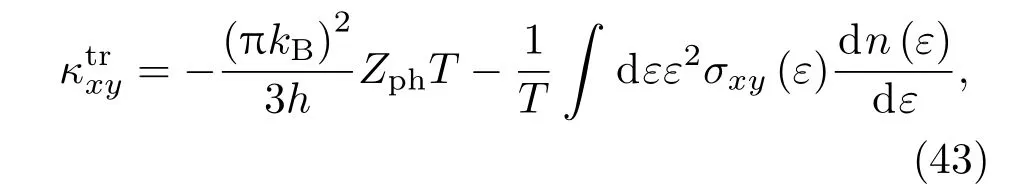
这里[16]
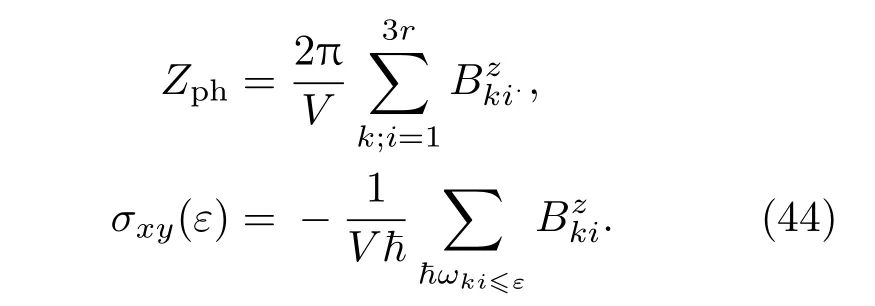
从上述公式中可以看出声子的霍尔热导率由其色散关系和Berry曲率所决定,这与量子霍尔电导有一定的类比性[4].
此外,通过半经典的波包动力学方法,可以研究热霍尔效应,包括电子热霍尔效应、磁振子霍尔效应以及声子霍尔效应.在热霍尔效应中,可以定义粒子磁矩为
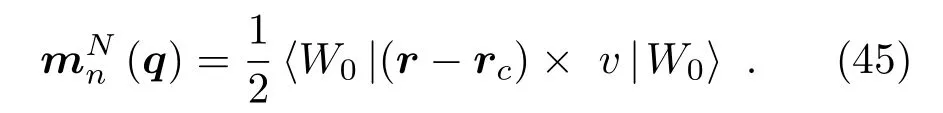
故体系的能量和热磁矩分别为
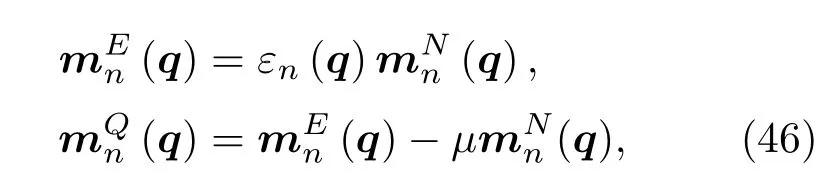
这里εn是布洛赫能带的能量,µ是化学势.类比于电子轨道磁化,热轨道磁化MQ有两个部分,一个来自于波包的自转有关,记为;另一个是波包中心的运动的贡献,将其表示为[18].
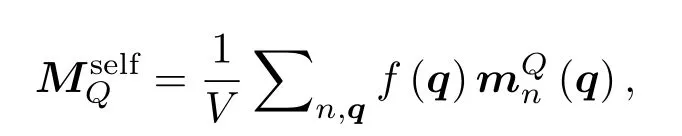
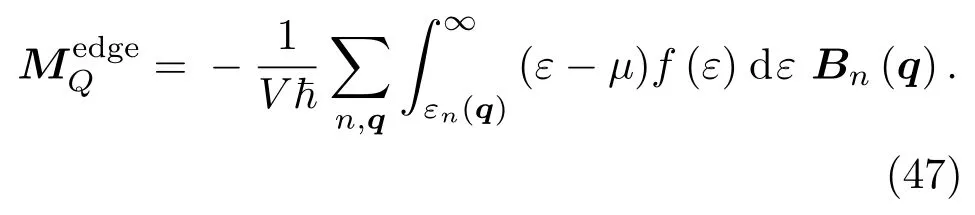
可以得到总的热流为
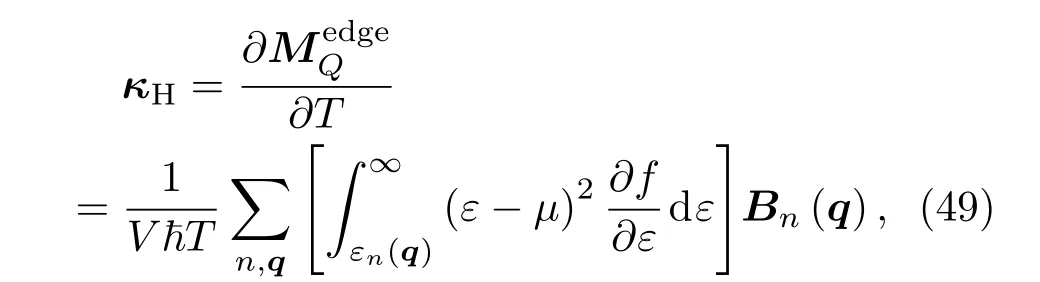
此公式是电子霍尔热导、磁振子霍尔热导以及声子霍尔热导的通用公式.其中对于声子可以进一步写成:
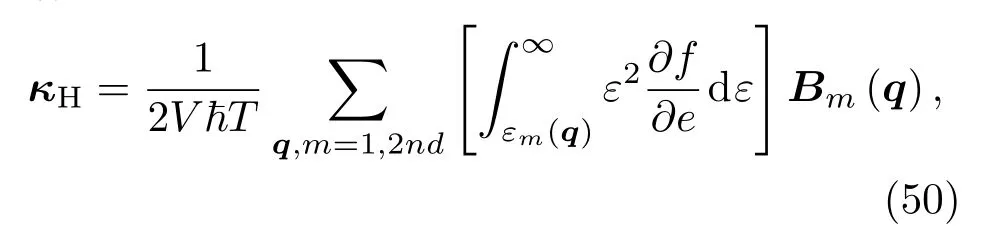
其中n,d分别是原胞内的原子数和每一个原子的自由度.
3.3 声子霍尔效应的拓扑性质
由于本证矢量的波矢依赖性,可以计算其Berry相效应.通过 Berry近似,首先设x(t)=, 并代入上式中. 由于 Berry相,所以Berry曲率可写成
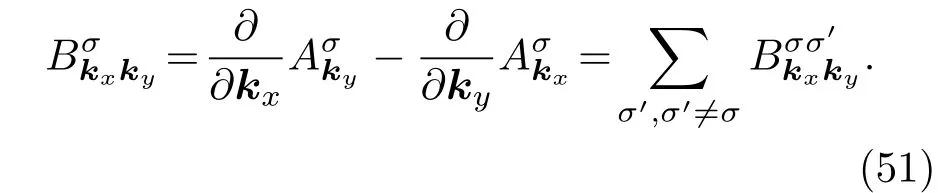
然后通过将第一布里渊区域上的Berry曲率整合得到相关的拓扑陈数:
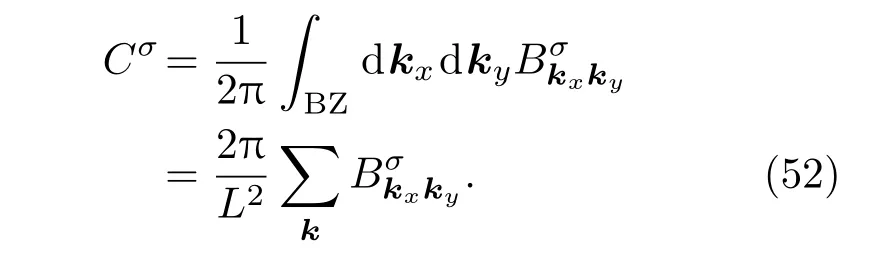
如果没有拉曼自旋声子的影响,也就是说当h=0时,此时 Berry曲率处处为零,声子的霍尔热导率消失.当外加磁场作用时,Berry曲率不为零,因此,声子霍尔效应也随之出现.另外研究发现,如果体系出现对称性满足SDS−1=D,SAS−1=−A,此时声子的霍尔热导为零[31],此时如果磁场改变了,Berry曲率也会改变,但是陈数在很大的范围内并不改变.尽管陈数被量化了,但是由于(40)式中f(ωσ)(ωσ+ωσ′)2项的存在,声子的霍尔热导率并没有被量化.

图2 (a)—(d)当临界磁场hc− =hc−10−2rad/ps时能带1到4的Berry曲率轮廓图;(e)—(h)当临界磁场hc+=hc+10−2rad/ps时能带1到4的Berry曲率轮廓图;从(a)—(h)水平轴和垂直轴分别对应于波矢kx和ky;(i)在不同磁场中的Berry曲率,实线和虚线分别对应于在临界磁场为hc−时Ω2和Ω3,相应的实点和虚点分别对应于临界磁场为hc+时Ω2和Ω3;(j)四种能带的陈数C1(实线),C2(虚线),C3(点线),C4(虚点线);(k)在临界磁场为hc附近的不同磁场下能带2和能带3的色散关系图,其中虚线、实线以及点线分别对应于在临界磁场为hc−,hc,hc+时的带[15]Fig.2.(a)–(d)The contour map of Berry curvatures for bands 1–4 at hc− =hc− 10−2rad/ps;(e)–(h)the contour map of Berry curvatures for bands 1–4 at hc+=hc+10−2rad/ps;for(a)–(h),the horizontal and vertical axes correspond to wave vector kxand ky;(i) Ω at di ff erent magnetic fields,the solid and dashed lines correspond to Ω2and Ω3at hc−,respectively,while dotted and dash-dotted lines correspond to those at hc+;(j)Chern numbers of four bands,C1(solid line),C2(dashed line),C3(dotted line),and C4(dashdotted line);(k)the dispersion relation of bands 2 and 3 at di ff erent magnetic fields in the vicinity of hc,the dashed,solid and dotted lines correspond to the bands at hc−,hcand hc+,respectively[15].
随着磁场的增加,在临界磁场hc的附近,发现存在拓扑相变.不同频带在靠近临界磁场的Berry曲率由图2(a)—(f)给出,当hc附近磁场变化非常小时,在Γ点附近的能带2和能带3的Berry曲率几乎是完全不同的,而能带1和能带4却保持不变.如图2(i)所示,在临界磁场上方和下方Berry曲率发生了急剧的变化,从而导致能带2和3的陈数发生跳跃,如图2(j)所示,这个跳跃表明两条带的拓扑结构在临界磁场下突然改变,这与能带结构的相变有着重要的联系[15].
为了进一步研究声子拓扑带结构变化的机理,同样给出了在临界磁场附近的声子的色散关系图,如图2(k)所示,可以看到当磁场增加到hc时,在Γ点附近能带2和能带3彼此的相互靠近.同样,在临界磁场区域,两条能带发生了简并且两条带的形状出现了锥形.而在临界点hc上方,两条能带发生了分裂.也就是说在临界磁场附近的声子的色散关系直接影响了Berry曲率,从而导致拓扑相变.
这里提出的声子霍尔热导率的拓扑学方法是一般的,可以应用于低温下的真实材料.最近的研究发现它也可以用于磁霍尔效应[32].从拓扑性质和色散关系来解释的声子霍尔效应相变也可以推广到研究其他霍尔效应或非平衡运输中的相变.
4 声子谷霍尔效应
4.1 谷电子霍尔效应
由于空间反演对称性的破坏,动量空间里分开的不等价的能谷K,K′,通过Berry曲率或轨道磁矩可以来描述这种不等价性.因此这两处不等价的能谷便构成了除电荷和自旋以外电子的另一个自由度,这也导致了能谷电子学的出现.
自然界大量存在类似于石墨烯的六角蜂窝状晶格层状材料,例如氮化硼、硒化镓、过渡金属二硫化物等.不同于石墨烯,这些材料中的A和B子格是由不同的原子构成,从而体系破坏了空间反演对称性.这些材料也为研究能谷电子学提供了条件.
在A/B堆积的双层石墨烯材料中,通过施加垂直与二维平面的电场来打破石墨烯的空间反演对称性,从而在K和K′能谷处产生大小相等但反向的并且与能谷相关的Berry曲率及轨道磁矩[33].因此也带来了一系列新奇的效应,如能谷霍尔效应[34].如图3,在非零的Berry曲率和外加面内电场的作用下,谷电子获得反常的大小与Berry曲率成正比[35,36]的横向速度,不同的谷电子偏转方向相反.因此在样品两端可探测到谷极化电流,图中Berry曲率的反差使得K和K′能谷电子在垂直外加电场方向的运动发生横向相反方向的偏转,这就是谷电子霍尔效应.最近,实验上已经在单层二硫化钼三极管[37]和石墨烯超晶格[38]中观测到了谷电子霍尔效应.
通过对称性分析可知,破坏时间反演对称性或破坏空间反演对称性的系统中声子携带非零的角动量.在这一部分,我们引入非磁性的六角AB晶格体系,即破坏空间反演对称性,但保留时间反演对称性.在两个不等价的能谷处手性的声子大量集中,即谷上的声子是左旋或者右旋圆极化的,且非简并的声子模可以用量子的赝角动量标记[17].所以,类比谷电子霍尔效应,对于谷声子,自然要提出两个问题:谷声子的Berry曲率是否为零?如果Berry曲率是非零的,是否存在谷声子霍尔效应?
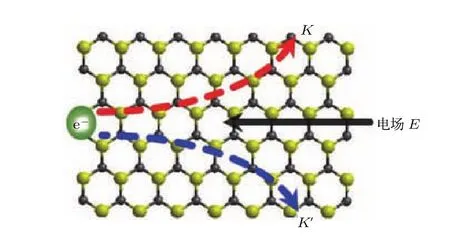
图3 谷电子霍尔效应示意图[34]Fig.3.Valley electronic Hall e ff ect diagram[34].
4.2 声子Berry曲率
之前计算声子的Berry曲率,采用传统的晶格动力学周期解
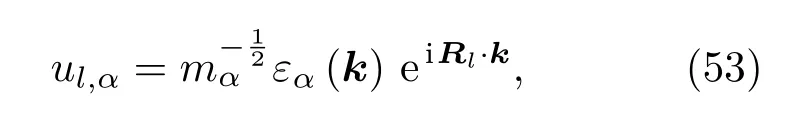
这里的u和ε是维度为2(二维运动)或3(三维运动)的列向量.接着可以得到运动方程
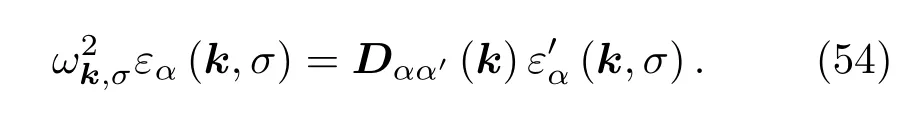
而实际上,为了准确地得到声子的Berry曲率,必须考虑到原胞内格点的相位差,因此这里采取布洛赫波形式的声子波函数
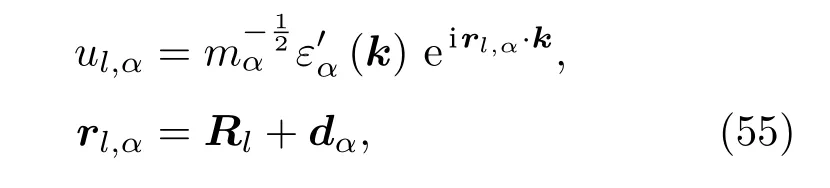
其中dα是第α原子相较于第l个原胞的平衡位置,因此可以得出
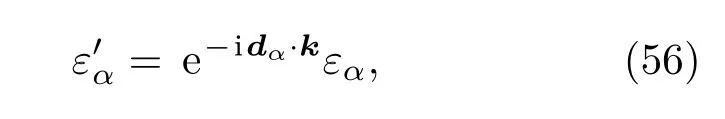
所以动力学矩阵变为
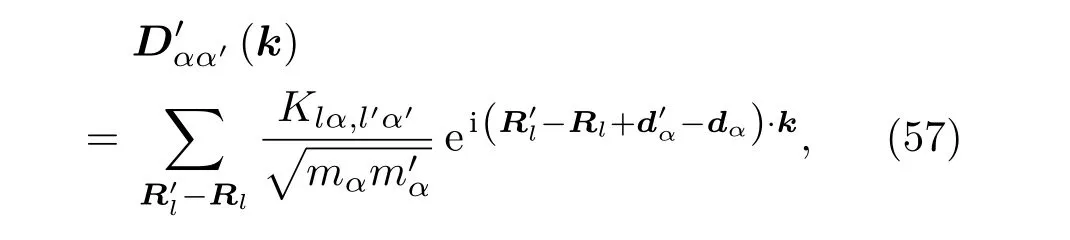
此时的运动方程为
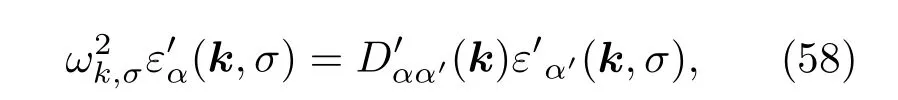
这与之前的运动方程是等价的,它们具有相同的色散关系,仅仅是波函数相差了一个相位.
在第二节已经计算过声子的Berry曲率,这里由于具有时间反演对称性,只需考虑所有正的声子模.
由于ε(k,σ)=ε∗(−k,−σ), 在时间反演对称性的保护下, 有ε(k,σ)=ε∗(−k,σ), 所以因此
类比于电子的Berry曲率计算Hψn=Enψn,声子的Berry曲率为
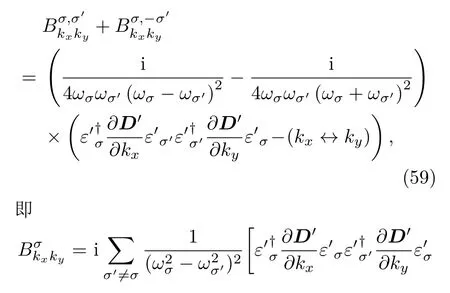

这一形式也与第二节所给的声子Berry曲率相符合.
4.3 谷声子霍尔效应
非磁性的六角A/B晶格体系破坏了空间反演对称性,如图4(a),在能谷处观察到了非零的声子Berry曲率.能带1和能带4在能谷处拥有较大的Berry曲率,而能带2和能带3在能谷处的Berry曲率较小.正因为能谷处存在非零的Berry曲率,施加纵向的应变梯度Estrain,类比于谷电子霍尔效应,会出现与应变梯度和Berry曲率的叉矢成正比的反常速度,νanom∝−Estrain×B.因此,被左旋或者右旋极化光子激发的位于不同能谷处的声子会沿横向移动.如图4(b)和图4(c),如果光子的极性反转,那么横向声子流的方向也会翻转.随着声子在某条边的积累,可以测得横向的温度差.很显然,如果圆极化的受激光子极性反转,则横向温差也会相反.
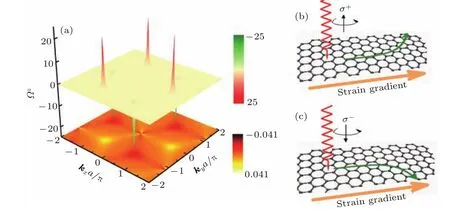
图4 六角A/B晶格的声子贝里曲率和谷声子霍尔效应 (a)能带1(底部二维图)和能带2(顶部三维图)的Berry曲率;(b),(c)谷声子被右旋或左旋极化光激发(霍尔热流由红色箭头标出),在应力梯度下产生相应的声子[17]Fig.4.Phonon Berry curvature and valleyphonon Hall e ff ect in a honeycomb of A/B lattice:(a)Berry curvatureof band 1(bottom contour plot)and band 2(top 3D plot);(b),(c)schematic of the valley phonon hall e ff ect(the Hall current denoted by the olive curve arrows)undera strain gradient(the orange arrows),where valley phononsare excited by a ray of right-handed or left-handed polarizedlight(the red wave lines)[17].
声子霍尔效应已在实验上证实[39],在顺磁绝缘体中,磁场可以改变声子的输运,因此可以测得横向的温度差,但是其效应受限于及其微弱的自旋声子相互作用.在破坏空间反演对称性而保持时间反演对称性的体系中,非零的Berry曲率诱发的谷声子霍尔效应确实广泛存在于六角晶格中,将会有更大范围的应用.
5 同时破坏时间和空间反演对称的声子模型
由于时间反演对称破缺会产生具有非零拓扑陈数的声子态,即声子霍尔效应,其具有单向导通的不受散射的声子边界模式;空间反演对称破缺会产生具有非零的Berry相的谷,可用作调控声子输运的新型量子自由度,即谷声子霍尔效应;如果两种对称性破缺同时存在,则能产生新的拓扑相变并演生出丰富的声子拓扑量子态.

图5 (a)由A/B晶格组成的蜂窝状晶格示意图,以及在K和K′声子谷附近的狄拉克锥;(b)当同时破坏掉时间反演和空间反演对称两个谷的频率不变,其中A/B晶格声子态A由红色标出,B由蓝色标出[19]Fig.5.(a)A honeycomb lattice composed of A/B sublattices,and the Dirac cones of phonons near the K and K′valleys;(b)the two valleys that arenondegenerate in frequency caused by breaking P and T simultaneously[19].
Liu等[19]的最新研究中,利用类似于Haldane蜂窝晶格模型,研究并探索Berry相与声子的拓扑效应.在这种晶格中,纵向光学和声学模式在K处形成线性交叉条带和 Dirac点,如图5所示.当破坏空间反演对称性以及时间反演对称时,哈密顿量可以写成:
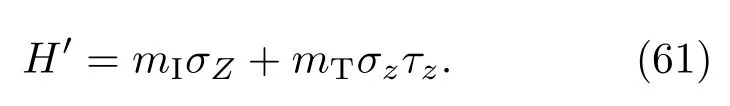
在上述的介绍中,我们已经了解了单独破坏时间反演对称或者空间反演对称对Berry曲率的影响,此时Berry通量在每个谷中的值为±π,且陈数CK(K′)=±1/2. 由于C=CK+CK′,故在单独破坏时间反演时,Berry曲率B(k)=B(−k),陈数为C=±1,此系统中可以观测到声子霍尔效应;在单独破坏空间反演对称时,B(k)=−B(−k),陈数C=0,可以观测到谷声子霍尔效应.如图5所示,当同时破坏时间反演和空间对称性时,两声子谷之间的频率简并消失,K和K′之间的能带带隙打开且相互独立,即在极端情况下,只能在一个谷中实现零带隙能带,这种发现可以应用在声子谷滤波器中.
6 Berry相效应在其他声学体系中的应用
近几年,关于Berry曲率在声学体系中的应用的研究很多,例如在低温的情况下,磁绝缘体中的自旋激发的热导率可超过声子的自发激发的热导率,但由于其电荷为中性的,故自旋波不会产生相应的热霍尔效应.然而,在戈薇晶格,Berry曲率与热导率之间有着紧密的联系,在实验中观察到κ随着温度或磁场的变化而发生符号反转,其与金属带之间的陈数通量的符号交替相关[40].其次,在电子和声子相互作用的系统中,量子霍尔效应与无耗散电流情况下霍尔电导率之间也有着紧密的联系,最近已经观察到,当电流增加到一个临界值时,对应于声速的载波漂移速度出现了一个戏剧性的耗散[41].在反转对称性破坏的非磁性系统中,Berry曲率诱导横向谷声子霍尔效应将产生一些新的应用.
对于谷赝自旋,由于其作为新型信息载体的潜力巨大且在动量空间中能标注能量极值的量子状态而引起了人们的关注[37,38,42,43].在最近的一项研究中,武汉大学刘正猷研究组从实验上在声波晶体中观察到了声音的拓扑谷输运现象[44],他们除了通过声场的空间扫描直接观察谷选择性边缘模式之外,还在急剧弯曲的界面中观察到抗反射现象.与传统声波导相比,拓扑保护的声音传输与其明显不同,这一发现可以作为设计具有非常规功能设备的基础.
另外,近期刘正猷教授研究组在声子晶体中首次引入谷自由度的概念,预测了声学谷态所具有的涡旋声场分布并提出了产生特定手性声涡旋场的方法,在此基础上,他们进一步实现了谷束分离和基于谷态的粒子操控.可以预期其潜在的应用与声学涡旋及物质的异乎寻常的相互作用,例如触发俘获的微粒的旋转而不接触.这一发现具有重要的科学意义[45].
此外,通过刚性键或者弹簧连接起来的质点组成的框架或格子模型构造在结构工程、建筑和材料科学等不同领域有着重要的应用.在这类晶格中,刚性键的数量与格子自由度之间的差异决定了它们的“零频率”软盘模式的数量.当这些平衡时,系统处于机械不稳定的边缘,被称为等静压.由于某些扩展的等静压晶格在其边界的软盘模式呈现局部化,这些边界模式对局部扰动不敏感,似乎具有拓扑起源,可联想到在量子霍尔效应和拓扑绝缘子中发生的受保护的电子边界模式.由此科学家们建立了拓扑机械模式和电子系统的拓扑带理论之间的联系,并预测了具有不同边界模式的新的拓扑大体积机械相的存在[46].
最近,科学家在机械拓扑绝缘子中观察到声子的螺旋边缘态,这一发现使得利用表面声子的稳定性设计可靠的波导的拓扑声学材料成为可能[47].在具有单向弹性边缘波的拓扑声子晶体中,科学家们通过使用陀螺惯性效应来打破时间反演对称,实现电子量子(反常)霍尔效应的声子模拟,研究结果激发了新型表面波器件的设计热潮,将广泛应用于电子、电信和声学成像[48].
7 展 望
拓扑物理学是一个方兴未艾的领域,有着很广泛的前景等待着科学家们去开发.自从量子霍尔效应发现以来,凝聚态物理中的拓扑现象层出不穷,如拓扑绝缘体、拓扑超导体等.拓扑与声子学的结合才刚刚开始,已有的相关研究工作中已可看到很大的发展空间和广阔的应用前景.
在磁性体系中,声子霍尔效应的发现给声子输运与控制提供了新的方法,但至今没有更多的实验研究声子霍尔效应.由于绝大部分顺磁材料自旋声子相互作用很小,所以测得霍尔效应很弱,如何寻找更大效应的顺磁材料是一个挑战.另外铁磁绝缘体,由于更大的磁化率和更大的自旋声子相互作用,可以存在更强的的声子霍尔效应,但是由于其中的磁振子霍尔效应也很强,所以区分铁磁绝缘材料中热霍尔效应中磁振子和声子的贡献也是一个很有意义的课题,由于磁振子和声子的拓扑性质不一样,拓扑声子学在铁磁材料中声子霍尔效应可以发挥更大的作用.
块体能谱的拓扑特性实际上也对应着非平凡的边界态,那么对于这里的声子霍尔效应,理论上应该存在相应的拓扑保护的边界态或者边界模式,和磁振子一样声子等玻色子体系中都没有费米面的概念,所以真正意义上的玻色子拓扑绝缘体不存在,但是可以通过波导选择带隙中的模式,这样磁振子和声子拓扑绝缘体也可以存在.拓扑磁振子绝缘体已经发现,但是拓扑声子绝缘体还没有真正发现,寻找拓扑保护的边界声子模对于无耗散的声子输运控制及相关能量科学将具有潜在的应用价值.
谷声子霍尔效应为声子的控制提供了一个新的自由度.由于电子的谷间散射与谷声子紧密联系,如最近发现的谷声子具有确定的手性并且决定电子谷间散射的选择定则[16],因而谷声子对谷电子学的发展意义重大.对于谷声子相关理论,以及不同模型和材料中的手性声子计算还需广泛深入的研究.另外实验直接观测谷声子以及谷声子霍尔效应也是一项具有重大意义的研究.
对于同时破坏时空对称性的体系,谷声子的能量简并打开,为实现单谷声子的选择与应用提供了思路.而如何找到这样的材料还有待进一步的探索研究.
拓扑声子学才刚刚开始.而拓扑与自旋电子学的结合已经引领了凝聚态物理几十年.我们相信,由于声子在凝聚态物理中广泛存在,如超导、电声相互作用、布里渊区及拉曼散射、热电效应、热效应等,拓扑声子在这些领域中不可回避并起到关键作用,也将引领凝聚态物理学的蓬勃发展.
[1]Berry M V 1984Math.Phys.Sci.392 45
[2]Wilczek F,Shapere A 1989Geometric Phases Phys.5 05857
[3]Prabhakar S,Melnik R,Bonilla L L 2014Phys.Rev.B89 245310
[4]Thouless D J,Kohmoto M,Nightingale M P,den Nijs M 1982Phys.Rev.Lett.49 405
[5]Karplus R,Luttinger J M 1954Phys.Rev.95 1154
[6]Zeng C,Yao Y,Niu Q,Weitering H H 2006Phys.Rev.Lett.96 037204
[7]Hasan M Z,Kane C L 2010Rev.Mod.Phys.82 3045
[8]Qi X L,Zhang S C 2011Rev.Mod.Phys.83 1057
[9]Li B,Wang L,Casati G 2004Phys.Rev.Lett.93 184301
[10]Chang C W,Okawa D,Majumdar A,Zettl A 2006Science314 1121
[11]Li B,Wang L,Casati G 2006Appl.Phys.Lett.88 143501
[12]Rikken G L J A,Strohm C,Wyder P 2002Phys.Rev.Lett.89 133005
[13]Inyushkin A V,Taldenkov A N 2007JETP Lett.86 379
[14]Sheng L,Sheng D N,Ting C S 2006Phys.Rev.Lett.96 155901
[15]Zhang L,Ren J,Wang J S,Li B W 2010Phys.Rev.Lett.105 225901
[16]Qin T,Zhou J,Shi J 2012Phys.Rev.B86 104305
[17]Zhang L,Niu Q 2015Phys.Rev.Lett.115 115502
[18]Zhang L 2016New J.Phys.18 103039
[19]Liu Y,Xu Y,Duan W 2017 arXiv preprint arXiv:1707.07142
[20]Zhou J H 2012Ph.D.Dissertation(Beijing:Institute of Theoretical Physics,Chinese Academy of Sciences)(in Chinese)[周建辉 2012博士学位论文 (北京:中国科学院理论物理研究所)]
[21]Nagaosa N,Sinova J,Onoda S,MacDonald A H,Ong N P 2010Rev.Modern Phys.82 1539
[22]Kagan Y,Maksimov L A 2008Phys.Rev.Lett.100 145902
[23]Wang J S,Zhang L 2009Phys.Rev.B80 012301
[24]Zhang L 2011Ph.D.Dissertation(Singapore:National University of Singapore)
[25]Holz A 1972Nuovo Cimento B9 83
[26]Strohm C,Rikken G,Wyder P 2005Phys.Rev.Lett.95 155901
[27]Kronig R L 1939Physica6 33
[28]van Vleck J H 1940Phys.Rev.57 426
[29]Wang L and Li B 2007Phys.Rev.Lett.99 177208
[30]Zhang L,Ren J,Wang J S,Li B W 2011J.Phys.Condens.Matter23 305402
[31]Zhang L,Wang J S,Li B 2009New J.Phys.11 113038
[32]Onose Y,Ideue T,Katsura H,Shiomi Y,Nagaosa N,Tokura Y 2010Science329 297
[33]Xiao D,Yao W,Niu Q 2007Phys.Rev.Lett.99 236809
[34]Zeng H L,Cui X D 2016Acta Phys.Sin.45 505
[35]Chang M C,Niu Q 1996Phys.Rev.B53 7010
[36]Xiao D,Chang M C,Niu Q 2010Rev.Mod.Phys.82 1959
[37]Mak K F,McGill K L,Park J,McEuen P L 2014Science344 1489
[38]Gorbachev R V,Song S J C,Yu G L,Kretinin A V,Withers F,Cao Y,Mishchenko A,Grigorieva I V,Novoselov K S,Levitov L S,Geim A K 2014Science346 448
[39]Cao T,Wang G,Han W P,Ye H Q,Zhu C R,Shi J R,Niu Q,Tan P H,Wang E,Liu B L,Feng J 2012Nat.Commun.3 887
[40]Hirschberger M,Chisnell R,Young S,Lee N P 2015Phys.Rev.Lett.115 106603
[41]Heinonen O,Taylor P L,Girvin S M 1984Phys.Rev.B30 3016
[42]Xu X D,Yao W,Xiao D,Heinz T F 2014Nature Phys.10 343
[43]Rycerz A,Tworzydlo J,Beenakker C W J 2007Europhys.Lett.79 57003
[44]Lu J Y,Qiu C Y,Ye L P,Fan X Y,Ke M Z,Zhang F,Liu Z Y 2016Nature Phys.13 369
[45]Lu J Y,Qiu C Y,Ke M Z,Liu Z Y 2016Phys.Rev.Lett.116 093901
[46]KaneC L,LubenskyT C 2013arXivpreprint arXiv:1308.0554
[47]Süsstrunk R,Huber S D 2015Science349 47
[48]Wang P,Lu L,Bertoldi K 2015Phys.Rev.Lett.115 104302
PACS:66.70.–f,03.65.Vf,72.10.Bg,72.15.GdDOI:10.7498/aps.66.226601
*Project supported by the National Natural Science Foundation of China(Grant No.11574154).
†Corresponding author.E-mail:phyzlf@njnu.edu.cn
Topological phonons and phonon Hall e ff ects∗
Xing Yu-Heng Xu Xi-Fang Zhang Li-Fa†
(School of Physics and Technology,Nanjing Normal University,Nanjing 210023,China)
28 September 2017;revised manuscript
6 November 2017)
The combination of topology and physics is a new field of physics development in recent decades.It is not only active in quantum field theory and high energy physics,but also widely exists in condensed matter physics,including quantum(anomalous,spin)Hall e ff ect and topological insulators(superconductors)etc.Phonon,as the main carrier of heat transport in the crystal,recently,due to the discovery of various phonon devices,phonons has been widely concerned by scientist.In this paper,we introduce the topological properties of phonons and the phonon hall e ff ect.We have reviewed the related physical research progress of phonon hall e ff ect,phonon valley hall e ff ect and so on,which are generated by breaking the time reversal symmetry,spatial inversion symmetry,both breaking the time and spatial inversion symmetry.Finally,the application of topology in other acoustic systems is brie fly introduced,and the future development direction is discussed too.
topology,Berry phase,Berry curvature,phonon Hall e ff ect
10.7498/aps.66.226601
∗国家自然科学基金(批准号:11574154)资助的课题.
†通信作者.E-mail:phyzlf@njnu.edu.cn

