二维振动紧实台振动力大小及方向控制原理

蒲 军

（陕西法士特汽车传动集团有限公司铸造分公司，陕西宝鸡 722409）

二维振动紧实台振动力大小及方向控制原理

蒲 军

（陕西法士特汽车传动集团有限公司铸造分公司，陕西宝鸡 722409）

本文介绍了一种消失模铸造造型用二维振动紧实台的结构，并研究了振动力大小和方向的控制原理。利用动量守恒定律，建立起四个振动电机偏心块在转动过程中转速及相互间相位差，与振动紧实台振动力大小及方向之间变化关系的数学模型。通过分析发现，振动紧实台振动力的大小与偏心块的转速的平方成正比；振动力的方向则由在转动过程中偏心块间的相位差决定。

消失模；振动紧实台；振动力矢量控制

振动紧实台是消失模铸造中的关键设备之一。消失模铸造的振动紧实台，产生高频振动，使砂箱内干型砂受到振动力的作用，在砂层内产生挤压力，同时振动波也在砂层内迅速传播，砂粒之间摩擦力的大小和方向也随之不断变化，使砂粒之间的咬合能力大大削弱，型砂流动性显著提高。型砂在挤压力的作用下，在良好流动性的促进下，克服摩擦力由挤压力大的区域向着挤压力小、密度小的区域移动，完成充填和紧实的任务。目前，振动紧实台通常采用振动电机作为驱动源，结构简单，操作方便，成本低。根据振动电机的数量及安装方式，可以分为一维振动紧实台、二维振动紧实台、三维振动紧实台。

l 复杂铸件振动紧实台选择

当前使用消失模工艺生产的铸件类型越来越多，其中有许多形状结构较为复杂的高附加值铸件，如汽车涡轮增压器中间壳体、发动机缸体、发动机缸盖等。这些复杂高端铸件在生产中通常都存在模样死角部位难以填砂和白模模样变形这两个问题。这是因为在振动作用下，型砂的流态化程度毕竟有限，向下和水平方向的填充能力较好，而向上的充填能力就十分有限。所以，当铸件存在填充死角时，就需要选择二维或三维振动紧实台，通过控制振动力大小和方向，形成满足充填要求的定向型砂运动和强弱可调的均匀激振力，来完成填充。

2 二维振动紧实台的结构

如图l所示，该振动紧实台采用抱夹式结构，砂箱四周被振动框架所包围，四个空气弹簧充气将框架抬升，框架上的四个砂箱支撑将砂箱托起，四个夹紧油缸伸出压紧砂箱，四个振动电机沿振动系统的重心对称分布。

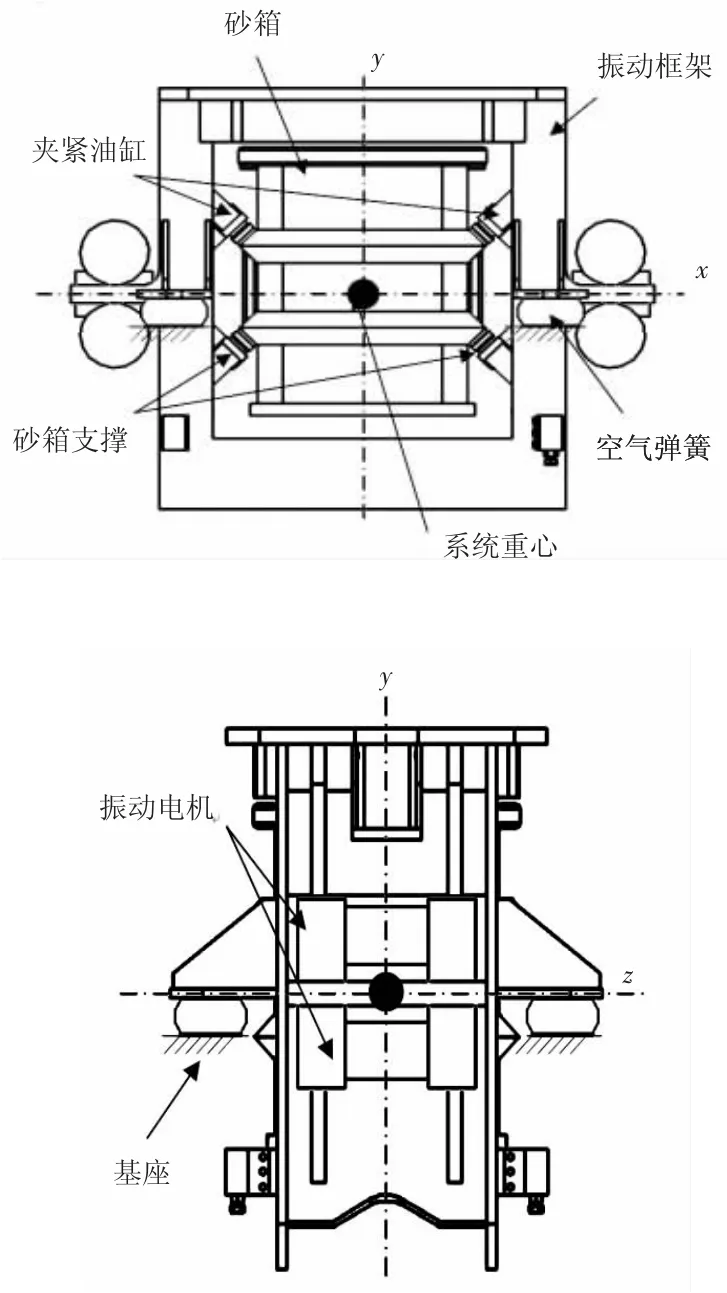
图l 二维振动紧实台的结构

3 参振部分满足动量守恒定律

参振部分包括：砂箱、砂箱内型砂、振动框架、四台振动电机，总重量约为：7 0l3 kg.

振动电机参数：5.5kW，2极，额定转速3000rpm，最大激振力62.4 kN.

S——振动设备的双振幅，m；

F——激振力，N；

n——振动电机转速，r/min;

W——振动机械设备的参振重量，kg.

可得，在四台振动电机的共同作用下该振动紧实台的最大双振幅：，

对于由振动框架、振动电机、砂箱及砂箱中的型砂组成的参振系统，只受到重力和空气弹簧的支撑力这两个外力的作用，在静止时合力为零，在振动时所受外力的合力为系统偏离平衡位置后产生的回复力。回复力大小为：

FMax合=4×△F，

△F——弹簧力（N），△F=k×△X；

k——空气弹簧刚度（kN/m）在使用高度时，0.5 MPa压力下，空气弹簧的刚度为47l kN/m；

△X——空气弹簧变形量，m.

得：FMax合=4×△F=4×k×S/2=4×47l×l03×（0.722×l0-3/2）≈680 N.

在振动过程中，外力FMax合远远小于参振系统内力即振动电机产生的振动力FMax振，FMax振=4×62.4×l03=249.6 kN，所以满足动量守恒定律，可以认为该参振系统在振动时的总动量保持不变。

4 数学模型

为便于分析，将参振系统中四个振动电机偏心块分别简化为质点A、B、C、D，质量为m，偏心矩为r；其余参振部分简化为质点E，质量之和为M.如图2，X轴为水平方向，Y轴为垂直方向，在X-Y平面内，将各部分动量沿水平、垂直方向分解。由参振部分动量守恒，得到下面两个等式：

图2 4个振动电机偏心块质点简化图

maAx+maBx+maCx+maDx+Max=0

maAy+maBy+maCy+maDy+May=0

又由于m×a=F，F为作用在物体上的合力，

所以FAx+FBx+FCx+FDx+Fx=0

整理后得：

Fx——作用在质点E上的振动力沿X方向的分力；

Fy——作用在质点E上的振动力沿Y方向的分力。

如图3所示，当质点A以角速度ω旋转到相位角α时，FA为偏心块产生的振动力即振动电机A产生的振动力，振动力FA沿X轴和Y轴分解得：

FAx=FA振×cosα； FAy=-（FA振×sinα）.

同理，当质点B以角速度ω速度旋转到相位角β时，如图2所示，振动力FB沿X轴和Y轴分解为：

当质点C以角速度ω速度旋转到相位角γ时，如图2所示，振动力FC沿X轴和Y轴分解为：

因为

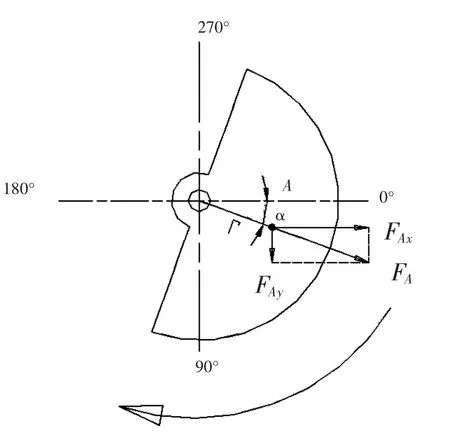
图3 A质点旋转

当质点D以角速度ω速度旋转到相位角δ时，如图2所示，振动力FD沿X轴和Y轴分解为：

振动电机振动力的计算公式为：F振=mrω2.

由于A、B、C、D四个振动电机的偏心块质量及偏心矩相同且转速相同，所以可得：FA振=FB振=FC振=FD振=F振=mrω2.

将各振动电机产生的振动力分量代入式（5）和式（6）得质点E受到的振动力为式（7）和式（8）：

5 振动力大小及方向的决定因素

5.1 振动力的大小

从式（7）和式（8）得，振动力的大小周期性变化，最大值与振动电机旋转角速度ω2成正比。

5.2 振动力的方向

振动紧实台工作时，四个振动电机同时以速度ω，按图2所示方向旋转。通过振动电机的控制系统，使偏心块B与A的相位角一致，使偏心块C和偏心块D比A的相位角提前l80°.

即 α=β=ω×t；γ=δ=ω×t+l80°，t为时间，代入式（7）和式（8）得：

可以看出，此时振动紧实台只受到水平方向上的振动力Fx作用，在振动的过程中，Fx的矢量图如图4线段l所示。其作用点在坐标（0，0）处，终点在线段l上游走，振动力大小和方向同余弦函数一样，周期变化，极限值为±mrω2.

在振动电机旋转的过程中，调整彼此间的相位差，使偏心块变为D与A的相位角一致，偏心块B和 C 比 A 的相位角提前 l80°. 即 α=δ=ω×t；β=γ=ω×t+l80°；带入式（7）和式（8），得 ：

此时振动紧实台变为只受到垂直方向上的振动力Fy作用，Fy的矢量图如图4线段2所示，其作用点在坐标（0，0）处，终点在线段2上游走，振动力大小和方向同正弦函数一样，周期变化，极限值为±4×ω2.

图4 振动矢量图

再次调整偏心块之间的相位差，当以偏心块A为基准，偏心块C和偏心块D的相位角提前l80°，偏心块B相位角提前量为60°.

即 α=ω×t；β=ω×t+60°；γ=δ=ω×t+l80°带入式（7）和式（8），得：

将 t作为变量，通过式（l2）和（l3）计算出振动力矢量在时间t时的终点坐标，得到如图5所示的一个以（0，0）点为中心的椭圆。于是振动紧实台受到的随时间周期变化的振动力矢量即可表示为：作用点在（0，0）位置，箭头指向椭圆上的点的线段，并且该线段以作用点为圆心，以速度ω旋转。可见，在振动的过程中，振动力的大小和方向是在不断变化的，但可以近似认为振动力的方向主要集中在椭圆的长轴方向上。同理，当偏心块B的相位角提前量分别为 90°、l20°、240°、270°、300°时，得到的由振动力矢量线段终点构成的椭圆分别如图5所示，可见随着偏心块B的提前量从60°增加到300°，振动力的方向绕（0，0）点逆时针方向旋转，一个特定提前量对应一个特定的振动力方向。

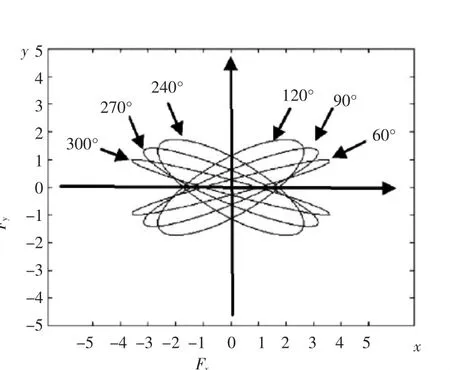
图5 振动矢量图

6 结论

l）该振动紧实台在振动过程中，振动力的大小与振动电机转速的平方成正比。通过控制转速就可以控制振动力的大小。

2）振动紧实台振动力的方向与四个振动电机偏心块在转动时的相位角有关。在振动的过程中，调整四个振动电机偏心块之间相位角的差值，就可以实现实时的振动力方向控制。

［l］孙耀天，吴剑.旧砂再生中激振力对旧砂搓磨力度的理论分析［J］.铸造设备与工艺，20l0（03）：9-ll.

［2］吴剑.一种筒式振动搓磨再生机的研究设计［J］.铸造设备与工艺，20l5（04）：l-2.

［3］吴剑.双质体落砂机在近共振区工作的振动机理分析［J］.铸造设备与工艺，20l2（03）：7-9.

［4］吴剑.振动机械结构优化设计的特性分析［J］.铸造设备与工艺，2009（03）：8-l0.

Control Principle of the Vibratory Force Magnitude and Direction of 2D Vibrating Ramming Platform

PU Jun
（Foundry Branch of Shanxi Fait Automotive Transmission Group CO.，LTD.，Baoji Shanxi 722409，China）

The structure of 2D vibrating ramming platform for lost-foam casting was introduced and the control principle of the magnitude and direction of vibratory force was researched.Based on the law of momentum conservation，the mathematical model of the relationship between the speed and phase of the eccentric block of four vibrating motors in the course of rotation and the magnitude and direction of the vibratory force was established.It was found that the magnitude of the vibratory force was proportional to the square of the speed of the eccentric block，and the direction of the vibration force was determined by the phase difference between the eccentric blocks.

lost-foam casting，vibratory compaction platform，vector control

TG23l.6

A

l674-6694（20l7）05-00ll-04

20l7-03-29

蒲军（l982-），男，陕西宝鸡人，工程师，工学学士，主要从事设备自动化工作。

l0.l6666/j.cnki.issnl004-6l78.20l7.05.002