一类比率依赖型捕食系统的稳定性分析

李建丽,张蓬霞

（长治学院数学系，山西长治046011）

一类比率依赖型捕食系统的稳定性分析

李建丽,张蓬霞

（长治学院数学系，山西长治046011）

研究了一类具有捕获项的比率依赖型捕食系统,讨论了系统正平衡点的存在性和各个平衡点的性态.它分析了非平凡正周期解的不存在性,构造lyaounov函数证明了该模型的正平衡点是全局稳定的结论,得到各个平衡点全局稳定性,并且研究捕食系统在各个平衡点下的最优收益,进而确定最优的捕获策略。

比率依赖；稳定性；最优收获；捕食模型

在捕获过程中,种群资源捕获不是恒定的,往往考虑因素较多,而比率型功能反应函数[1-8]的捕食系统更接近现实情况,所以讨论比率依赖的捕食系统更具实际意义。

将在此基础下研究以下模型:

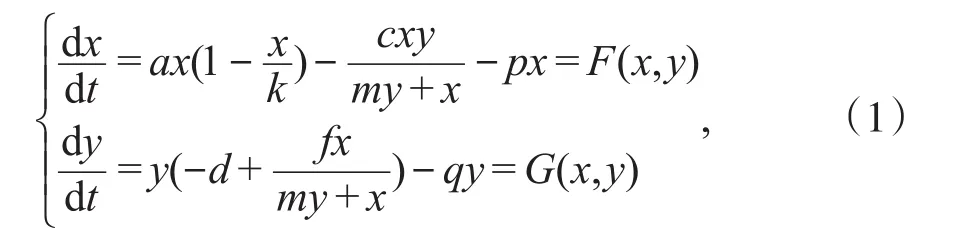
从生物学意义考虑,系统(1)满足条件

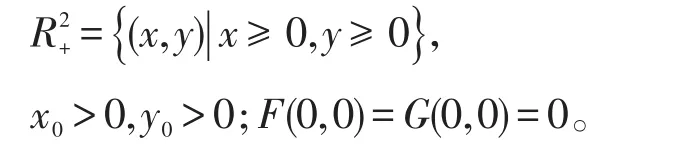
1 平衡点

1.1 平衡点的存在性

将系统无量纲化得

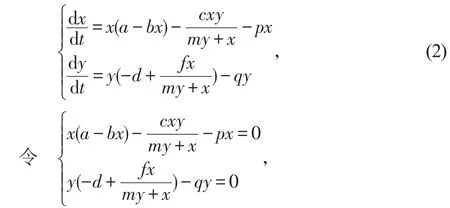
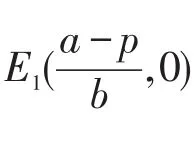
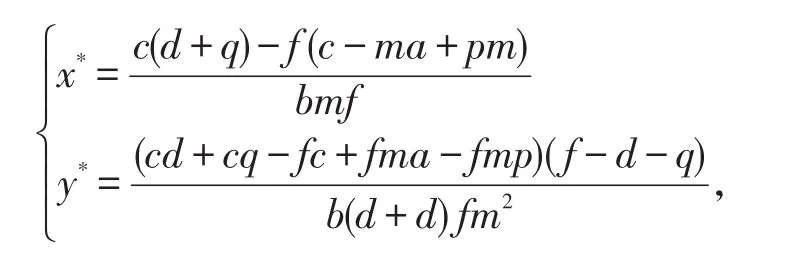
易验证E*(x*,y*)为唯一正平衡点的条件为

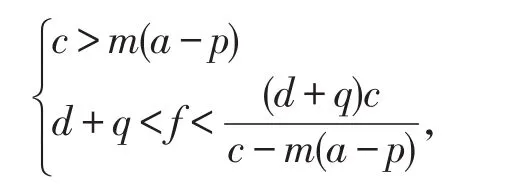
或者

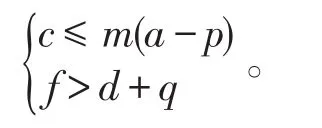
1.2 平衡点的稳定性

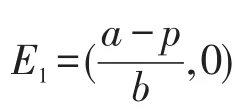
证明系统的雅克比矩阵为

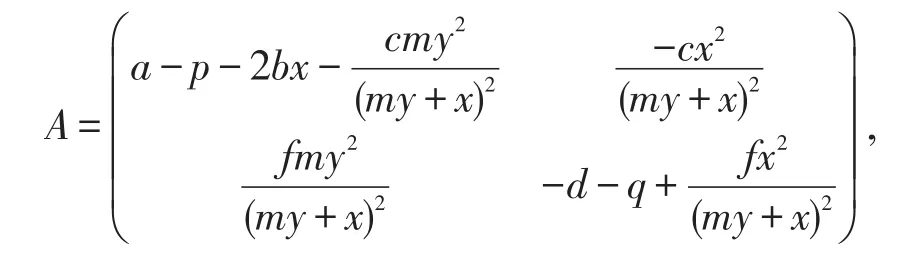
当f＜d+q时,若其特征多项式

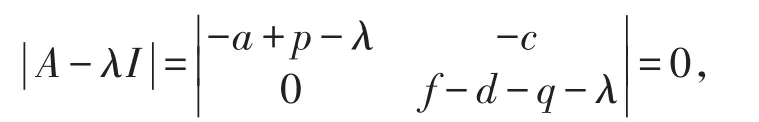
求解得到特征值

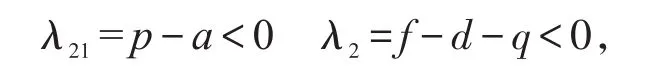
此时该雅克比矩阵的行列式

它的迹

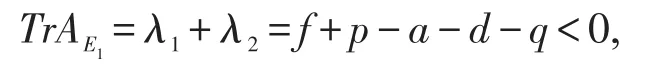
由捕食系统中方程知

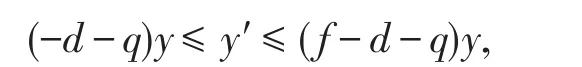
(1)若c＜m(a-p),则对∀ε∈(0,a-p),都存在T,使得当c≤m(a-p),f＜(d+q),有则

(2)若c=m(a-p)时,

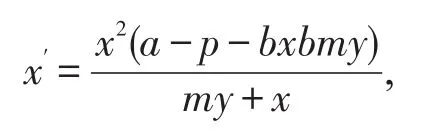
综上得,若c≤m(a-p),f＜(d+q),则模型的平衡点是全局渐近稳定的。

2 非平凡正周期解分析

由系统有唯一的正平衡点E*(x*,y*)可得

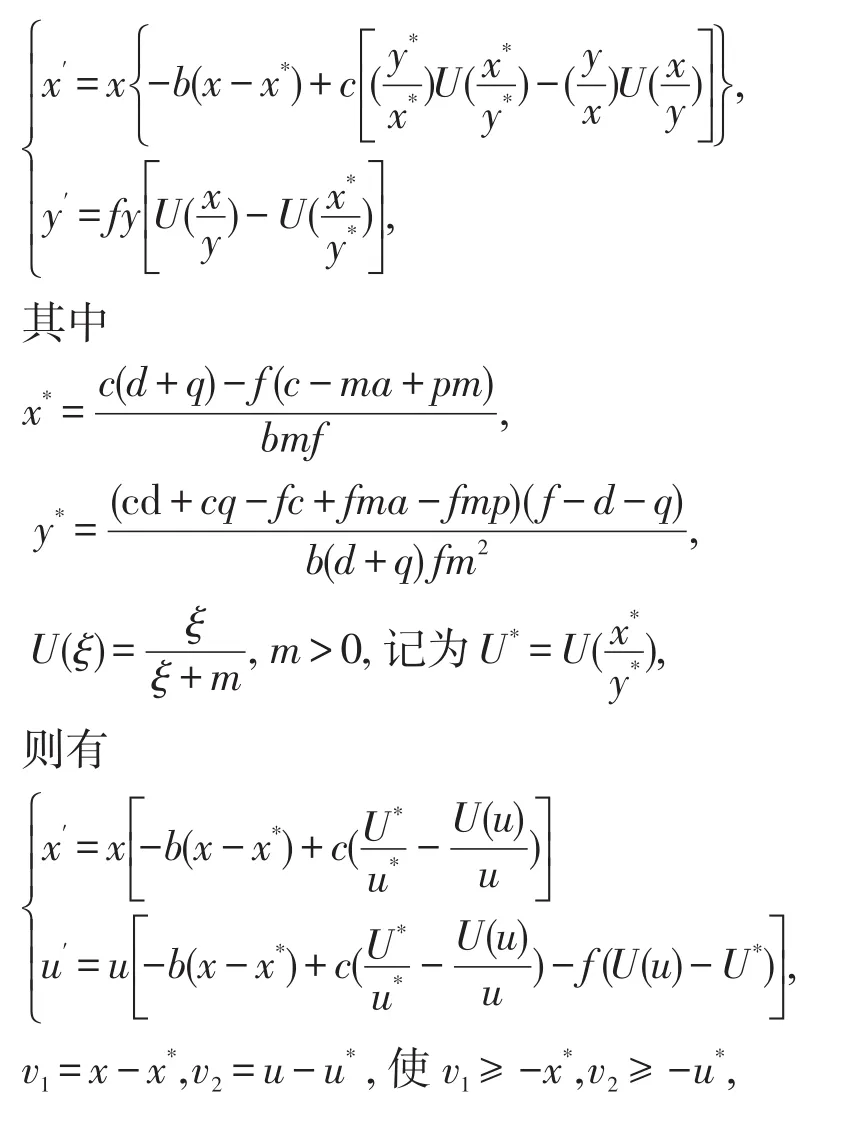
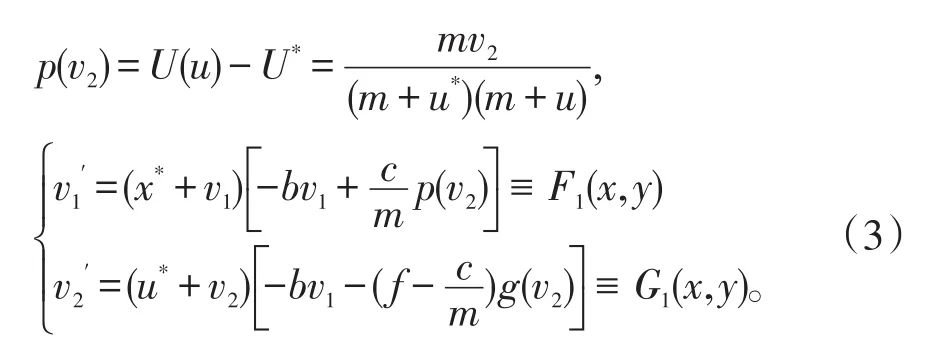
在同等条件下,系统(3)不存在非平凡正周期解令

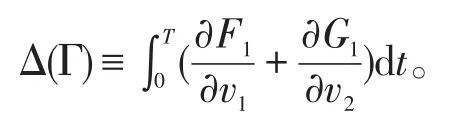
引理1若δ*=Tr(x*,y*)＜0，且c≤mf,则对于系统(3)在平衡点E*周围的所有正周期解有Δ(Γ)＜0 。

引理2 若δ*=Tr(x*,y*)＜0，且c＞mf,则对于系统(3)在平衡点E*周围的所有正周期解有Δ(Γ)＜0。

综上,由引理1,2[3]可得到如下定理:

定理3若系统(2)的正平衡态是局部渐近稳定的,则其没有非平凡正周期解,也就是所有的正周期解都趋近于O(0,0)或者E*(x*,y*)。

证明由上述条件和引理1,2得到,系统(2)无非平凡正周期解,而是鞍点且不稳定的,故系统(2)的所有的正周期解都趋近于O(0,0)或者E*(x*,y*)。

3 正平衡点的全局稳定性

定理4若系统(4)的唯一正平衡点E*(x*,y*)满足下列条件

(2)上述函数h(u)满足h′(u)＜0，且（u-u*)(h(u)-h(u*))≤ 0，

其中，

则E*(x*,y*)是全局稳定的。

证明由

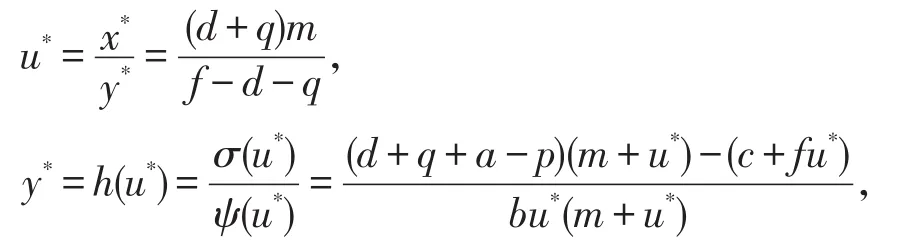
故正平衡点E*(x*,y*)的雅克比矩阵为

故正平衡点是局部渐近稳定的。

构造Lyapunov函数，

V函数在区域正定，且具有无穷大性质,对V(u,y)的t求导,得

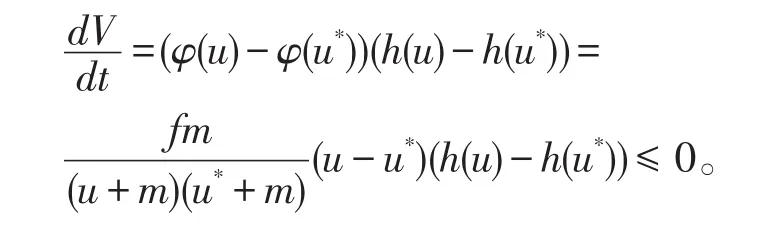
在定理条件下系统(4)的唯一正平衡点E*(u*,y*)是全局渐近稳定的。

4 最优捕获策略

设对捕食者和食饵的捕获强度为p,q,设捕食与食饵两种群的市场价格为p1,p2,若在生态系统下捕捞有意义,则必然要求每个平衡点的横坐标都大于或等于0[4],即满足条件:

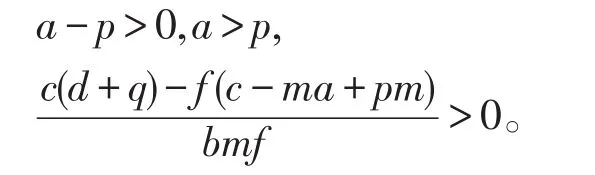
定理5系统(2)的三个平衡点满足上述条件,捕获能力有限,一定存在最优捕获策略。

证明 分别讨论不同平衡点下的捕获策略:

(1)对于平衡点O(0,0),Q=0,即捕获策略不当使两种群灭绝,所以经济效益为0。

(3)对于平衡点E*(x*,y*),其中

其中A=cd-fc+fma+cq-fmp，B=f-d-q，

根据方程解出p,q的值,代入Q,即可得到最大收益。则捕获策略可通过捕获食饵,捕食者的经济效益,最大收益为Q。

定理证明了如何决策捕获能力p,q,可获得最大收益Q,分配p,q捕获能力,可得到具体的收获策略。

5 结语

文章讨论了有捕获项的比率依赖的捕食系统的稳定性分析,通过对平衡点的研究,在不破坏生态环境下,得出什么情况对种群最大捕获量可得到最优收益,最终得到最优捕获策略。

[1]鲁铁军.一类基于比率的捕食-食饵系统的全局稳定性分析[J].应用数学和力学,2008,29(3):447-452.

[2]杜艳可,徐瑞,段立江.一类比率型捕食系统的定性分析[J].军械工程学院学报,2007,19(2):76-78.

[3]马知恩.种群生态学的数学建模与研究[M].合肥:安徽教育出版社,1996.

[4]马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001.

[5]王高雄.常微分方程[M].3版.北京:高等教育出版社,2006.

[6]黄建科.基于比率的三种群捕食模型的稳定性[J].江西师范大学学报,2007,11(6):588-590.

[7]张剑.一类比率型反应捕食模型的稳定性分析[J].数学的实践与认识,2011,41(10):198-204.

[8]堵秀凤.具有密度制约项的捕食食饵系统的捕食优化问题[J].高师理科学刊，2012,32(4):5-7.

〔责任编辑 高海〕

Stability Analysis of a Ratio-Dependent Predator-Prey System

LI Jian-li，ZHANG Peng-xia
(Department of Mathematics,Changzhi University,Changzhi Shanxi,046011)

In recent years,some hot topics of ratio-dependent functional response predator-prey system are studied by people.In this paper,a ratio-dependent functional response predator-prey system include harvested item is researched.The existence of positive equilibrium point and properties of every equilibrium point are discussed.It proves condition that the model has no nontrivial positive periodic solution.By constructing Lyapunov function,the globally asymptotic stabilities of every equilibrium point are obtained.At the same time,the optimal harvested problems of every equilibrium point are studied,then it get the optimal harvest strategy of system.

ratio-dependent;stability;optimal revenue;predator-prey model

O212

A

1674-0874(2017)05-0012-03

2017-05-20

山西省高等学校大学生创新创业训练项目[2015429];长治学院院级科研项目[201514]

李建丽(1983-)，女，山西高平人，硕士，讲师，研究方向:应用数学。