无资料地区山洪预警动态临界雨量计算

王晶娥

（辽宁省阜新水文局，辽宁 阜新 12300）

无资料地区山洪预警动态临界雨量计算

王晶娥

（辽宁省阜新水文局，辽宁 阜新 12300）

文章基于水位流量反推原理，以辽宁西部某无资料地区山洪为研究实例，计算该区域山洪预警的动态临界雨量，并结合二维水动力学模型对区域山洪进行了淹没范围分析。分析结果表明：水位流量反推方法可较好的解决无资料地区山洪预警动态临界雨量的计算问题，确定的不同时段临界雨量和区域实际情况较为吻合。山洪淹没分析可确定淹没水深和淹没范围，成果可为山洪预警和防洪决策提供重要依据。

水位流量反推法；动态临界雨量计算；无资料地区；山洪淹没分析；辽宁西部山洪预警

当前，流域内大江大河及中小河流的防洪体系已经基本架构完成，而小流域山洪由于受暴雨突发影响，呈现频发多发的态势，且山洪致灾损失十分严重，为此急需要对小流域山洪进行预警研究，从而为山洪灾害防治和防汛决策提供重要的依据。山洪预警的重要指标之一为区域的临界雨量，当前国内对临界雨量的计算进行了不同程度的研究［1-6］，但主要是针对有资料山洪地区的动态临界雨量计算，而对于无资料地区山洪临界雨量推算的研究相对较少。近些年来，随着各区域山洪非工程措施的逐步开展，急需要对一些无资料地区的山洪预警进行动态临界雨量的计算。目前，水位流量反推法在一些区域中小河流无资料地区的洪水预警中得到应用［7-9］，但是在山洪灾害洪水预警分析中应用还较少，特别是在辽宁西部无资料地区山洪预警动态临界雨量计算中还未得到应用。为此本文引入水位流量反推法，并以辽宁西部某无资料地区山洪为计算实例，对该实例的山洪预警动态临界雨量进行计算。

1 基于水位流量反推方法的山洪预警动态临界雨量计算原理

水位流量反推计算山洪预警动态临界雨量的基本原理为首先结合设计暴雨计算成果，得到区域不同频率下的设计暴雨曲线，再结合设计洪水计算，确定得到不同频率下的洪峰流量曲线，结合区域水位流量关系，确定不同致灾水位对应的成灾洪峰流量Q，应用确定的设计洪峰频率曲线反推得到相应的频率P，结合该频率和设计暴雨频率曲线，动态反推计算得到区域不同频率下的动态临界雨量，其主要计算方程包括设计暴雨和设计洪水的计算，计算方程如下：

首先计算设计点暴雨，其计算方程为：

式中，Pp-不同频率下的设计点雨量，mm；KP-皮尔逊Ⅲ型曲线模比系数；-P-不同时段的设计暴雨均值，本文设计时段选为 10min、1h、6h以及24h。

在计算设计点雨量的基础上，采用动点动面的方式进行点面折减计算区域的设计面暴雨量，计算方程为：

式中，Pp面-不同频率下的设计面雨量，mm；K-点面折减系数，其中点面折减系数的计算方程为：

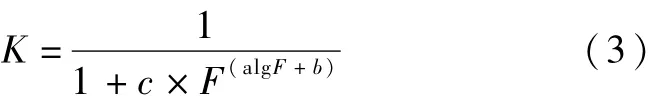
式中，a、b、c-计算系数，本文分别取为-0.027，0.925， 0.0016； F-设计区域的面积，km2。

在设计暴雨计算的基础上，需要进行设计洪水的计算，本文选用小流域设计洪水经验公式计算流域的设计洪水，计算方程为：

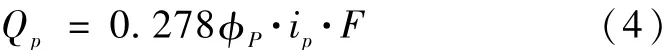
式中，φp-不同频率下的洪峰径流系数；ip-设计暴雨强度；F-设计区域面积。其中设计暴雨强度ip的计算方程为：

式中，τ-流域汇流时间，其计算方程为：

式中，L-计算河长，km；J-河段比降，‰；X和Y-流域下垫面特征参数，本文分别取为0.57和0.65。

本文结合二维水动力学方程计算小流域山洪的淹没范围，考虑文章篇幅原因，二维水动力学方程可详见参考文献［10］。

2 计算实例

2.1 区域概况

本文以辽宁西部某山洪小流域为计算实例，该区域的地形图见图1。区域集水面积为21.5km2，区域河长为11.27km，比降为12.1‰，为典型的山区性河流，区域内有2个行政村落。

图1 研究区域地形图

2.2 设计暴雨计算

根据沿河村落集水区（小流域）的位置查辽宁省暴雨参数图集中的年最大10m in、1h、6h、24h点雨量均值等值线图、点雨量Cv等值线图，得到各个小流域的相应时段的点雨量均值和；查暴雨洪水图集皮尔逊Ⅲ型曲线模比系数Kp值表，可得各计算单元不同设计暴雨频率相应的Kp值（见表1），乘以暴雨均值可得不同设计暴雨频率的设计点雨量，即可得到各时段的设计点雨量。

表1 小流域设计暴雨Kp系数表

根据辽宁省短历时暴雨时面深关系图，可得各小流域10min、1h、6h、24h、72h暴雨折算系数KF，乘以设计点雨量得到1h、6h、24h、72h的设计面雨量，小流域因汇流面积小于50km2，各时段KF均为1，由此得到研究小流域的设计暴雨成果。

表2 小流域设计暴雨成果表

2.3 设计洪水计算

在设计面暴雨和流域汇流时间计算基础上，结合公式（5）可计算得到区域不同频率的暴雨强度，结合辽宁省水文手册可得到区域不同频率的设计洪峰径流系数，各参数结构见表3。

表3 典型频率设计洪水参数表

在设计洪水参数确定的基础上，可以计算流域内2个防灾对象不同频率下的区域设计洪水成果，计算结果见表4。

表4 防灾对象推理公式法设计洪水计算成果表

2.4 水位流量关系的建立

在设计暴雨和设计洪水基础上，需要确定各防灾对象的水位流量关系，根据控制断面测量结果，采用曼宁公式法，确定防灾对象河道控制断面的水位流量关系，因各防灾对象没有水面线信息，可采用防灾对象的河床比降作为水位流量转换中的比降。因无实测水文资料，根据沟道特征，参照天然河道典型类型和特征情况下的糙率，确定水位流量转换中的糙率，以相邻流域水文站实测洪水资料的水位、流量、面积、湿周等，采用曼宁公式反推值进行校正，确定各个防灾对象控制河段河床的糙率值。根据以上方法，基于调查成果资料，确定各个防灾对象水位流量关系曲线，结果见图2。

图2 各防灾对象水位流量关系图

2.5 动态临界雨量计算

根据成灾流量和洪峰流量关系曲线可得到成灾流量对应的频率，结合暴雨频率曲线可以推算出临界雨量值，如表5、图3所示。

从表5中可以看出，随着时段的增加，1#和2#村落的临界雨量也逐步增加，1#村落不同时段的临界雨量在49～128mm之间，其汇流时间内的临界雨量为30mm。2#村落从第1时段到第24时段其临界雨量在88～249mm之间，其汇流时间的临界雨量为70mm，2#村落的临界雨量的等级均大于1#村落。从流域不同时段的临界雨量动态变化曲线（图3）中可以看出，各时段动态临界雨量变化曲线呈现较为明显的线性变化趋势，各时段动态临界雨量变化较为相似，具有一定的相似规律性，随着时间的增加，其临界雨量也逐步较大，表明山洪灾害与暴雨量以及暴雨强度都有较为密切的联系，从图3还可看出，降水中心在上游，区域的临界雨量雨大，降水中心的分布对区域临界雨量动态变化影响较大。

表5 小流域临界雨量成果表

图3 不同时段的临界雨量动态变化曲线

2.6 山洪预警指标综合分析

临界雨量是从成灾水位对应流量的洪水推算得到的，在数值上认为临界雨量即为紧急的预警指标；对于告知、警戒指标，在临界雨量基础上进行折减处理，得到研究小流域预警指标成果，预警指标结果见表6。

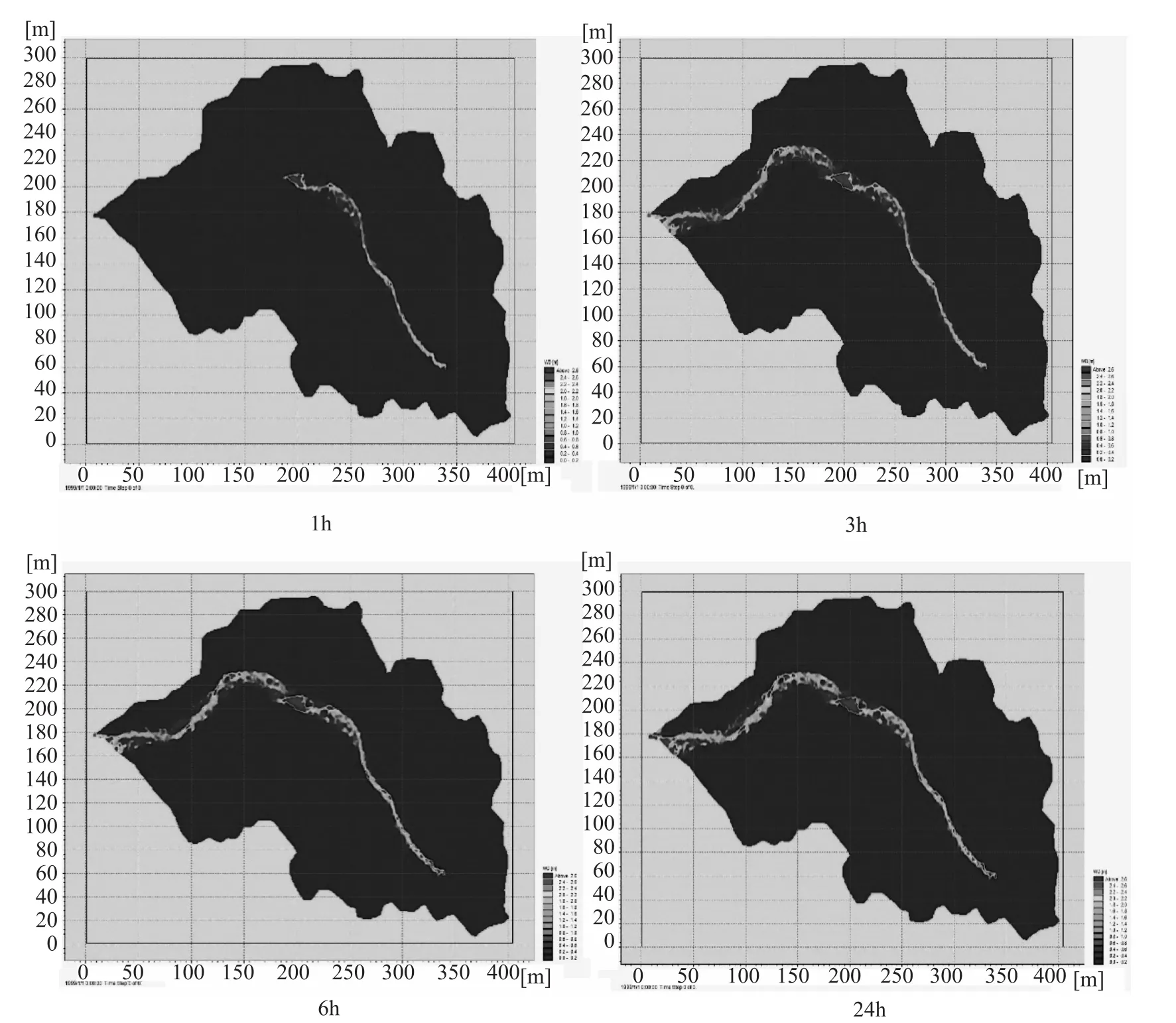
图4 区域不同时段淹没分析结果

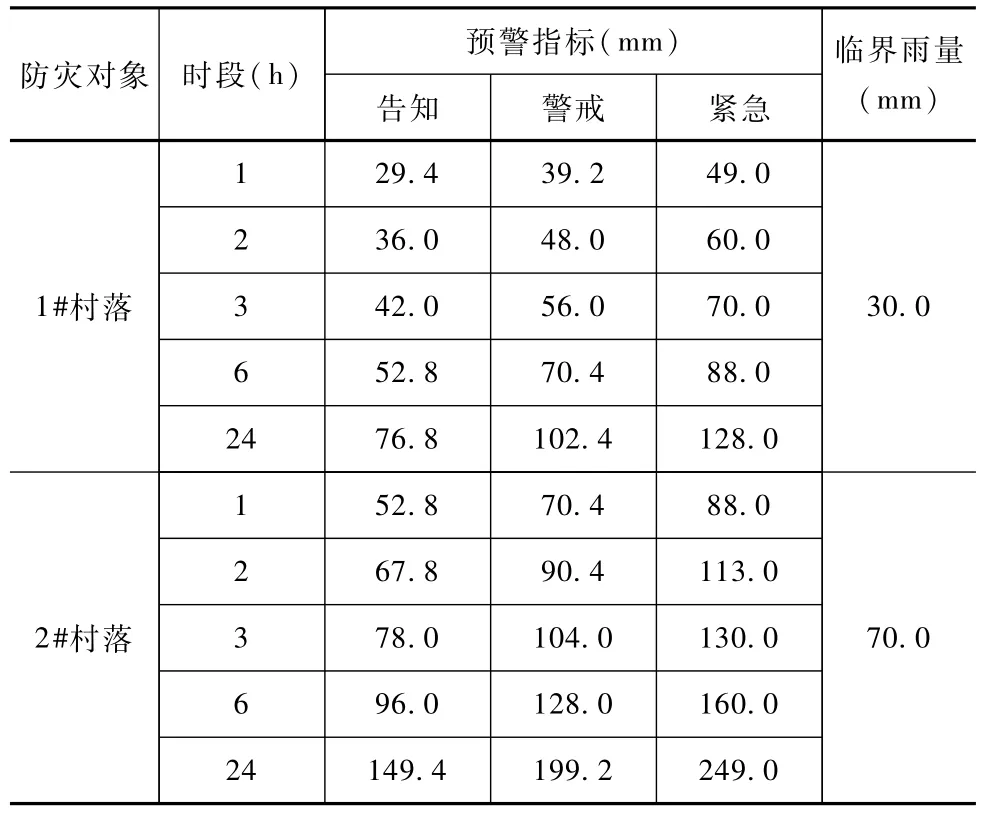
表6 设计小流域预警指标成果表

从表6中可以看出，1#防灾村落其不同预警等级的预警指标在29.4～128.0mm之间，这和区域暴雨特点情况较为吻合，区域不同时段2%频率下的暴雨在36.4～254.0mm之间，1#防灾对象预警指标在该范围之内，并且和区域实际暴雨特点较为吻合。2#防灾村落其不同预警等级的预警指标在52.8～249.0mm之间，由于其在下游，其预警雨量值均要大于1#防灾村落。综上设计小流域雨量预警指标结果可以看出，水位流量反推的动态临界雨量和区域实际情况较为吻合，适用于区域无资料地区山洪预警的动态临界雨量推求。

2.7 山洪淹没分析

在预警指标分析的基础上，本文结合二维水动力学模型对区域50年一遇不同时段的淹没范围进行了模拟分析，分析结果见图4。

从图4可以看出，研究小流域3h基本上水流已经达到流域出口，从50年一遇洪水最大淹没范围（最大淹没水深）可以看出，50年一遇洪水影响最大面积为1.89km2，水深小于0.5m的影响范围较小，淹没面积为0.48km2，而当水深大于3m时，其影响面积达到最大1.89km2，其影响面积较小的原因是因为流域地形原因，河道两边范围内地形较低，而周围地形均较高。从图中可以确定淹没范围，由于结果是矢量结果，可以应用地理信息软件提取淹没面积和淹没水深，为区域山洪预警提供决策依据。

3 结论

本文结合水位流量反推原理，以辽宁西部某无资料地区山洪为实例，计算该区域动态临界雨量，并结合二维水动力学模型对区域山洪进行淹没模拟分析，研究结论为：

（1）水位流量反推方法可解决无资料地区山洪预警动态临界雨量计算的问题，计算结果合理，可在山洪预警指标分析计算中进行应用和推广。

（2）降水中心在上游，区域的临界雨量大，降水中心的分布对区域临界雨量动态变化影响较大。

（3）流域受淹范围受地形条件影响较大，地势较低区域山洪淹没范围较大，淹没范围可为区域山洪预警提供重要的决策依据。

［1］毛北平.垂向混合产流模型在无资料地区山洪灾害临界雨量计算中的应用［J］.应用基础与工程科学学报，2016（04）：720-730.

［2］樊建勇，单九生，管珉，等.江西省小流域山洪灾害临界雨量计算分析［J］.气象，2012（09）：1110-1114.

［3］陈桂亚，袁雅鸣.山洪灾害临界雨量分析计算方法研究［J］.人民长江，2005（12）：40-43+54.

［4］祝武斌.甘肃省成县山洪灾害临界雨量分析计算［J］.水利规划与设计，2015（03）：26-28.

［5］段生荣.典型小流域山洪灾害临界雨量计算分析［J］.水利规划与设计，2009（02）：20-21+57.

［6］段生荣.典型小流域山洪灾害临界雨量计算分析---以黄河流域大通河支流为例［J］.中国农村水利水电，2008（08）：63-65+68.

［7］吴承卿.基于降雨～水位关系的临界雨量确定方法研究［J］.人民珠江，2016（11）：21-25.

［8］马传波.山区小流域洪水预警临界雨量值确定方法的研究与应用［J］.吉林水利，2016（06）：50-52+62.

［9］张玥，杨春辉，孟祥国.尾水位流量关系在尼尔基水库的应用［J］.东北水利水电，2015（07）：32-33+36.

［10］王春宇.基于二维水动力学模型的河流水力学特征分布研究［J］.水利技术监督，2016（04）：56-58+101.

P426.6

A

1672-2469（2017）10-0053-04

10.3969/j.issn.1672-2469.2017.10.015

2017-04-20

辽宁省水利厅科技指导计划性项目（2014-08）

王晶娥（1980年-），女，工程师。