不完全偏好序下考虑同事偏好的项目-员工匹配决策研究

□孙朝苑 董战英

[电子科技大学 成都 611731]

不完全偏好序下考虑同事偏好的项目-员工匹配决策研究

□孙朝苑 董战英

[电子科技大学 成都 611731]

针对具有不完全偏好序值信息的项目-员工匹配决策问题，给出了一种考虑同组员工间具有同事偏好关系的匹配决策方法。首先对匹配双方给出的不完全偏好序信息规范化处理，转化为等级置信度形式。其次，以规范化的等级置信度匹配信息为证据，融合获得项目与员工、员工与员工的融合总信度，并进一步转化为匹配满意度，以项目-员工、员工-其他员工的匹配满意度最大化为目标构建并求解考虑同事偏好的匹配决策模型。最后通过一个算例说明了所提方法的可行性和有效性。

同事偏好；匹配决策；不完全偏好序；证据推理

引言

双边匹配决策是指匹配双方主体利用获得的若干信息通过一定的方式对对方主体进行排序或择优，然后通过某种决策分析方法获得令匹配双方主体尽可能满意的匹配结果[1]。双边匹配问题最早起源于婚姻匹配问题和大学录取问题[2]。此后被逐渐应用于人力资源中员工与岗位的匹配问题[3]、贸易活动中买卖双方及合作伙伴的选择问题[4～5]、风险投资商与风险企业的匹配问题[6]等。

人力资源中的员工与项目的匹配问题作为人力资源管理中的关键环节已成为企事业单位关注的焦点。传统的员工与项目匹配决策中大多考虑一方匹配主体给出的关于另一方匹配主体的偏好信息，而现实生活中项目与员工匹配问题均涉及到同组或同群成员间的同事偏好关系，而这种偏好关系会影响到成员之间的协作配合程度，直接关系到该项目组的工作效率和质量。所谓的同事偏好即是指在项目和员工相互选择的过程中，员工之间存在的偏好关系，员工会根据其他员工的相关信息，如知识技能互补、熟悉程度等因素对彼此进行排序选择。理论研究中，Dutta和Masso最先提出了考虑同事偏好关系的匹配问题，定义了F-字典偏好，并利用DM模型证明了F-字典偏好下稳定匹配的存在性[7]。Echenique和Yenmez针对学生之间存在同事偏好关系的学生与学校的匹配问题，提出一种寻求稳定匹配的算法[8]。Kominers改进了[8]中的匹配方法，给出了可以确定任意经典多对一匹配问题的所有稳定匹配集合的算法[9]。Pycia在分割法和联盟环境下，研究了具有同事偏好匹配问题的稳定匹配方法[10]。Flanagan从合同匹配理论的角度研究了带有同事偏好的多对一匹配决策问题[11]。

已有的研究为进一步研究具有同事偏好的匹配决策提供了较好的思路和支撑，然而需要指出的是，现有研究中很少考虑匹配双方给出的偏好序中存在缺失和不确定的情况。而实际数据收集时，由于人们思维的模糊性和现实情况的复杂性，常出现不确定或不完全的信息。针对具有不完全不确定信息的匹配问题，不少学者也做出了相关研究，如：Iwama等提出具有不完全信息的匹配决策算法并应用于婚姻匹配问题[12]。Liu等研究了不完全信息下的稳定匹配问题[13]。Knoblauch研究了具有不完全偏好信息的不严格条件下的婚姻匹配，并分析了一边主体随机生成选择偏好的G-S算法及其性质[14]。乐琦等针对具有不完全不确定信息匹配问题，从匹配满意度的角度出发，构建了多目标匹配决策模型[15～17]。但现有的文献中处理不完全不确定偏好信息的方法多是将不确定偏好序信息看作为等概率的离散随机变量，求其期望，进一步以期望转化为满意度，这样将项目和员工匹配双方给出的匹配信息中不完全不确定信息等同于精确信息，导致匹配信息的丢失。综上，本文提出一种匹配决策方法，该方法将项目和员工给出的偏好序值信息转化为等级置信度的形式，保留了序值信息中的不完全不确定性，并利用证据推理融合序值信息，进一步转化为匹配满意度，以得到的项目和员工间的匹配满意度最大为目标，构建并求解考虑同事偏好的项目-员工匹配决策模型，通过算例说明了所提方法的实用性和有效性。

一、项目-员工匹配问题描述

在具有不完全不确定偏好序信息下考虑同事偏好的双边匹配问题中不仅要考虑匹配双方给出的不完全不确定偏好信息，还需要考虑同群或同组主体之间的不完全不确定偏好信息。因此，在双边匹配决策过程中需要考虑三个方面的满意度，即项目主体对员工主体的满意度、员工主体对项目主体的满意度，以及拟进入同一项目组的员工之间的满意度。

设项目主体集合A=｛A1,A2,⋅⋅⋅,Ai,⋅⋅⋅,Am｝，其中Ai代表第i个项目主体，i=1,2,⋅⋅⋅,m；员工主体集合B=｛B1,B2,⋅⋅⋅,Bj,⋅⋅⋅,Bn｝，其中Bj代表第j位员工主体，j=1,2,⋅⋅⋅,n。设为员工对项目的不完全不确定偏好序值信息，；特别地，若则员工对项目的偏好信息退化为精确偏好序值信息；若员工对项目的偏好序值信息，表示员工未给出对该项目的偏好序值信息。同理可设为项目对员工的不完全不确定偏好序值信息，；设为员工Bj对其他员工Bj的不完全不确定偏好序值信息，其中。

基于以上论述，本文要解决的问题是，考虑员工之间的同事偏好关系，根据员工、项目主体给出的不完全不确定匹配信息，如何通过一种有效的匹配决策方法快速得到令项目主体和员工均满意的匹配结果。

二、项目-员工匹配决策模型

针对上述问题，以下给出了不完全偏好序下考虑同事偏好的项目-员工匹配决策方法，该方法的具体思路为：将不完全不确定偏好序匹配信息转化为等级置信度的形式，利用等级置信度可以直接表达不确定信息以及证据推理能够处理不确定问题的特性，以等级置信度形式的匹配信息作为证据进行融合，保留匹配信息的不完全不确定性，获得融合总信度值，进一步转化为匹配满意度，构建和求解以双方匹配满意度最大化为目标的匹配决策模型，获得令项目和员工均满意的匹配结果。

（一）规范化项目-员工匹配信息

在具有不完全序值信息的考虑同事偏好的双边匹配问题中，项目主体、员工给出的不完全、不确定偏好序值信息，表示一方主体将另一方主体排在了第rL至rU位，且rL或rU越小，则另一方主体的排序位置越靠前，一方主体对另一方主体评价越好，若r表示该主体对另一方主体的具体排序，则r可看作是上具有等概率信息的离散随机变量，因此的概率向量可表示为，其中[18]。

因此可对项目主体、员工给出的相关偏好序信息进行规范化处理，具体如下：

若员工Bj对项目Ai的偏好信息为，则记H=｛H1,H2,⋅⋅⋅,Ht,⋅⋅⋅,Hm｝，其中Hi为员工Bj将项目Ai排在了第t位，t=1,2,⋅⋅⋅,m。则可以转化为：，其中

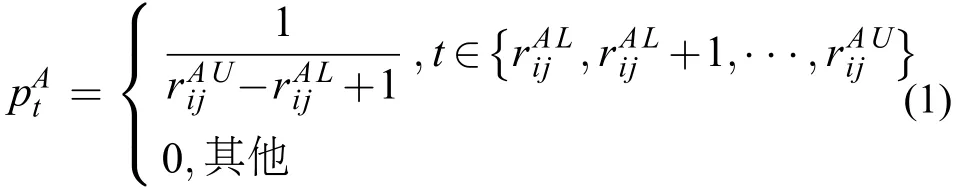
例1：员工-项目匹配过程中存在8个项目，员工Bj对项目Ai的偏好信息为，则可转化为：

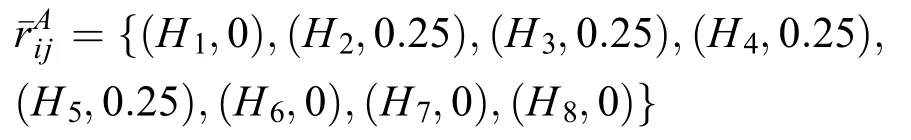
类似的，将Ai对员工Bj偏好信息转化为：；员工Bj对其他员工偏好信息转化为：。

当偏好序信息存在缺失值时，如：员工Bj对项目Ai的偏好信息，并不能认为Bj将Ai排在任意位置的可能性相等，只能作为信息的缺失，因为不等同于所表达的意思才是Bj将Ai排在任意位置的可能性相等。因此本文将转化为，记HN表示信息不确定，则，当表示信息完全不能确定。

（二）融合项目-员工匹配信息

考虑到证据推理方法解决了证据理论中的悖论问题并可以有效地对若干个不确定的子问题进行融合[19]，可以有效地保留项目、员工给出的偏好序信息的不完全不确定性，因此本文采用证据推理对规范化的项目、员工的等级置信匹配信息进行融合。

为了便于融合，首先对等级数目进行统一规范化，根据文献[20]中等级效用确定方法可知，最高等级的效用值为1，最低等级的效用值为0。即：员工Bj对项目Ai的偏好排序的等级效用值为：t=1,2,⋅⋅⋅,m；项目Ai对员工Bj的偏好排序的等级效用值为：。对不同等级形式进行规范化时，可根据相对地位进行规范化处理，所谓的相对地位即是效用值一样，鉴于等级个数一般为奇数，以下m、n默认为奇数，若m（或n）为偶数，则转化方法中的m（或n）可统一替换为2m-1（或2n-1），具体如下：

令等级集合为H=｛H1,H2,⋅⋅⋅,HC+1｝，C为(m-1)与(n-1)的最小公倍数，根据效用值相同的原理，可将HA下分别转化为：

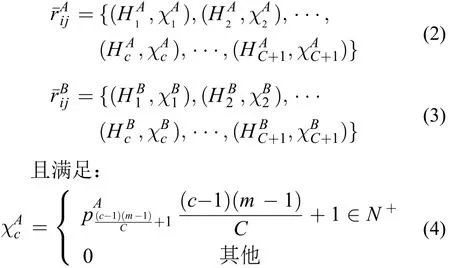
例2：项目A1给出员工B1的偏好排序为，B1给出A1的偏好排序，m=5，n=7。

A1对B1的偏好排序：

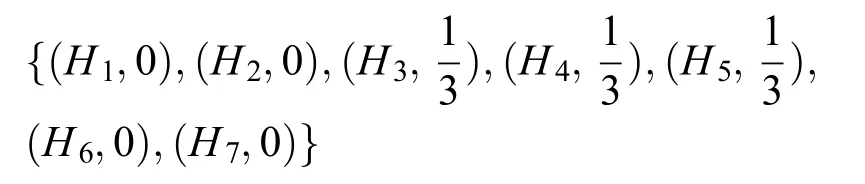
B1对A1的偏好排序：

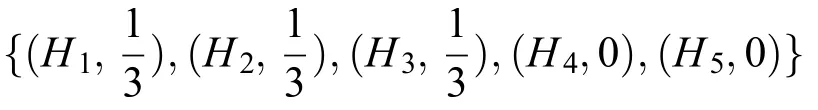
C为(m-1)与(n-1)的最小公倍数，即C=12，则A1对B1的偏好排序和B1对A1的偏好排序均可以转化为等级数为H=｛H1,H2,⋅⋅⋅,H13｝下的偏好排序，具体如下：

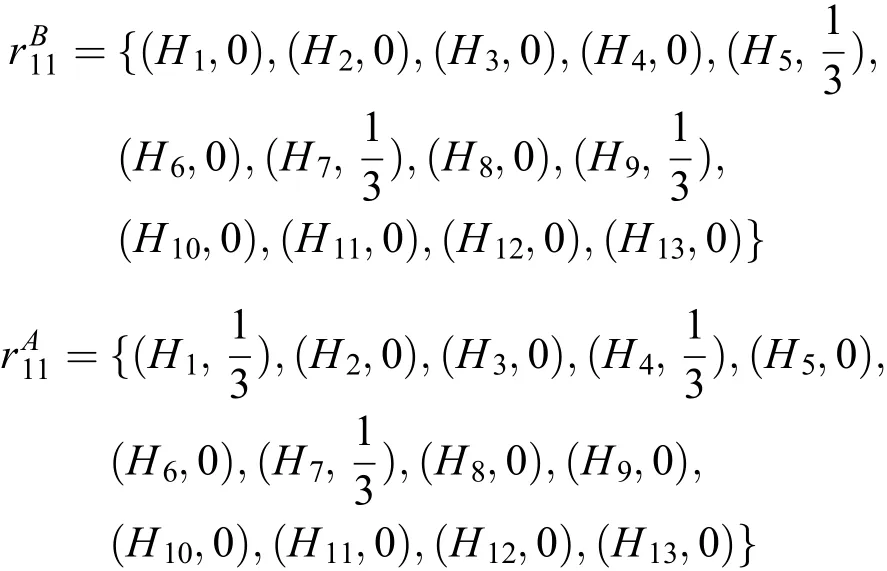
经过以上转化，偏好序信息均转化为H=｛H1,H2,⋅⋅⋅,HC+1｝下的等级置信度，可利用证据推理分别对员工Bj对项目Ai和项目Ai对员工Bj的等级置信形式的匹配信息进行融合。

设mk,A表示员工Bj对项目Ai的偏好信息在评价等级Hk的基本概率设置，mH,A表示未设置给任意评价等级H的基本概率，，其中是由于权重而引起的信度；是由于偏好信息的不完整引起的信度，mk,B表示项目Ai对员工Bj的偏好信息在评价等级Hk的基本概率设置，mH,B表示未设置给任意评价等级H的基本概率，，其中是由于权重而引起的信度；是由于偏好信息的不完整引起的信度，则：

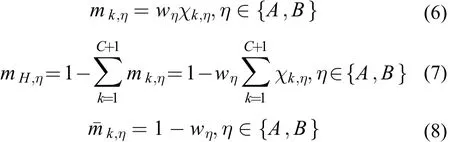
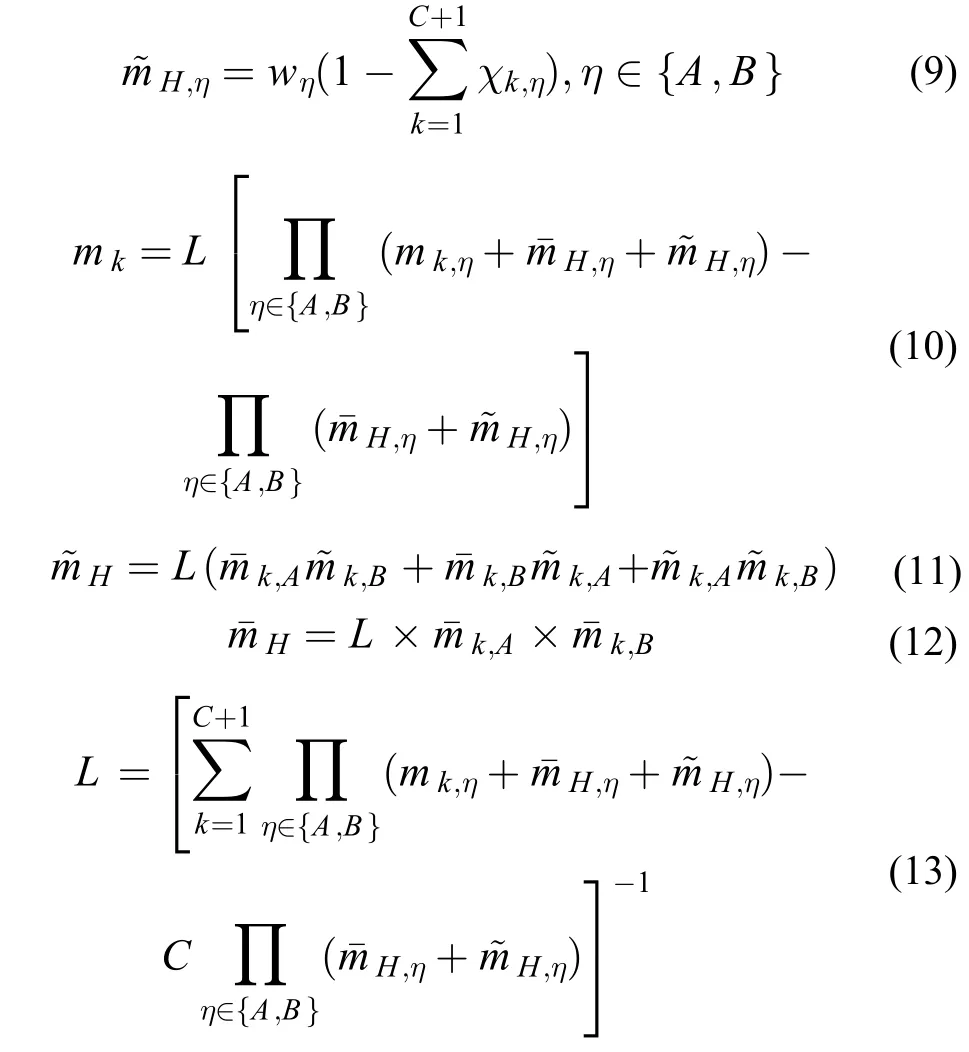
经过证据融合后，可以得到员工Bj和项目Ai的融合总信度值：

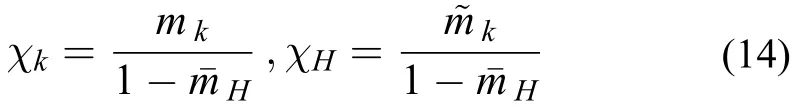
（三）构建项目-员工匹配决策模型

基于上节计算的融合总信度值，可根据匹配决策者对不确定信息的态度（如：乐观、悲观、折中）选择不同的方法将融合总信度值转化为满意度[19]，并获得项目Ai与员工Bj的融合满意度、员工Bj和员工的融合满意度，

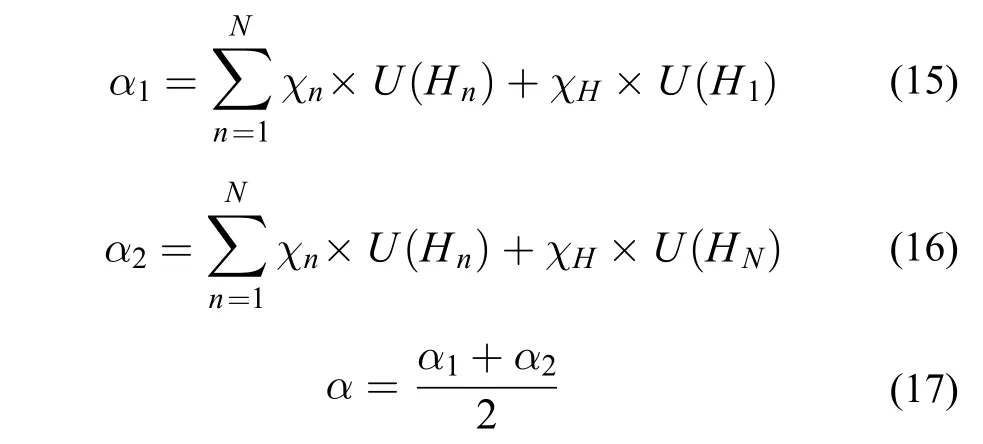
式（15）、式（16）、式（17）分别为乐观、悲观、折中态度处理不确定信息的情况下融合总信度转化为满意度公式。

基于获得的项目主体与员工的融合满意度、员工与其他员工融合满意度，引入0-1变量xij，xij=1表示员工Bj与项目Ai进行了配对，xij=0表示员工Bj与项目Ai未配对，xijxij′的取值表示员工Bj和Bj′是否均与Ai配对，xij、xij′取值均为1时，Bj和Bj′均与Ai配对，Bj与Bj′成为同事，综合考虑项目与员工之间的偏好关系以及同一项目组中员工间存在的偏好关系，建立如下多目标非线性匹配决策模型。

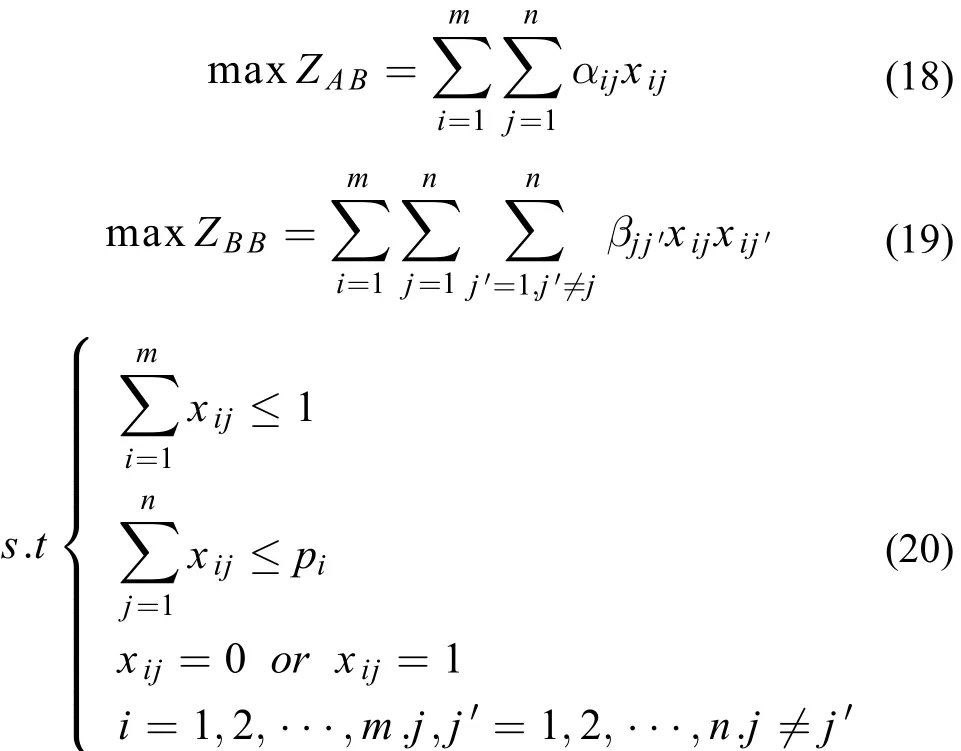
模型中的式（18）表示项目主体与员工主体的融合满意度最大化，式（19）表示员工主体B对成为其同事的其他员工的融合满意度最大化，式（20）表示每一位员工至多只能进入一个项目，每个项目可以选择多名员工，其中Pi为项目Ai所需员工的人数。

为求解上述匹配模型，考虑到融合满意度α、β量纲一致，可采用线性加权的方法将上述匹配模型转化为单目标匹配模型，优化模型可采用蚁群算法等智能优化算法进一步求解。

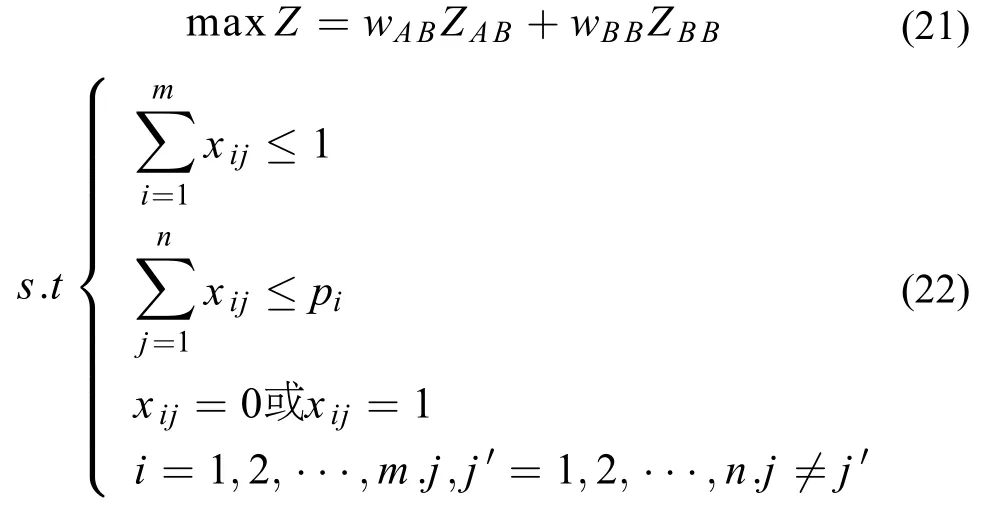
综上所述，不完全偏好序下考虑同事偏好的项目-员工的匹配决策方法步骤如下：

步骤1：获取项目、员工给出的偏好序匹配信息；

步骤2：将项目、员工给出的相关偏好序匹配信息规范化处理，转化为等级置信度形式，如式（1），针对员工和项目等级数目不同的情况，利用式（2）～式（5）将不同等级扩展为相同等级；

步骤3：根据规范化的匹配信息，利用式（6）～式（14）对匹配信息证据融合，获得员工和项目的融合信度值及员工与员工的融合信度值；

步骤4：根据获得的融合信度值采用不同的决策态度如式（15）～（17）得出融合满意度，根据融合满意度设计和求解匹配模型，即式（18）～式（22），得到匹配结果。

三、算例分析

成都市某电力公司，由于公司业务的扩展，现准备向新疆、西藏、青海、宁夏、甘肃五个省份大力推广产品，而目前该公司业务部有13名员工可接受外派，该公司根据各省份的整体市场规模裁定新疆（A1）需要业务员3名、青海（A2）需要业务员3名，西藏（A3）需要业务员2名，甘肃（A4）需要业务员3名，宁夏（A5）需要业务员2名，员工根据业务扩展省份的业务规模、工作强度、工作环境等对省区进行了排序，由于业务员需到陌生的环境进行工作，他们希望与自己分配到同一省区的业务员是自己熟悉的或与自己关系好的业务员，并提供了与其他业务员优先合作顺序，另一方面市场总监根据每个省区的情况对业务员进行了排序具体如表1、表2、表3所示。

充分考虑业务员与省区的偏好排序，为了获得令双方都满意的匹配结果，首先对业务员、省区给出的相关偏好序匹配信息规范化处理，针对业务员和省区分别为5个等级和13个等级，利用式（2）～式（5）将等级统一扩展为13个等级；根据规范化的匹配信息，利用式（6）～式（14）对匹配信息证据融合，以项目主体A4和员工主体B6为例，融合过程简述如下：

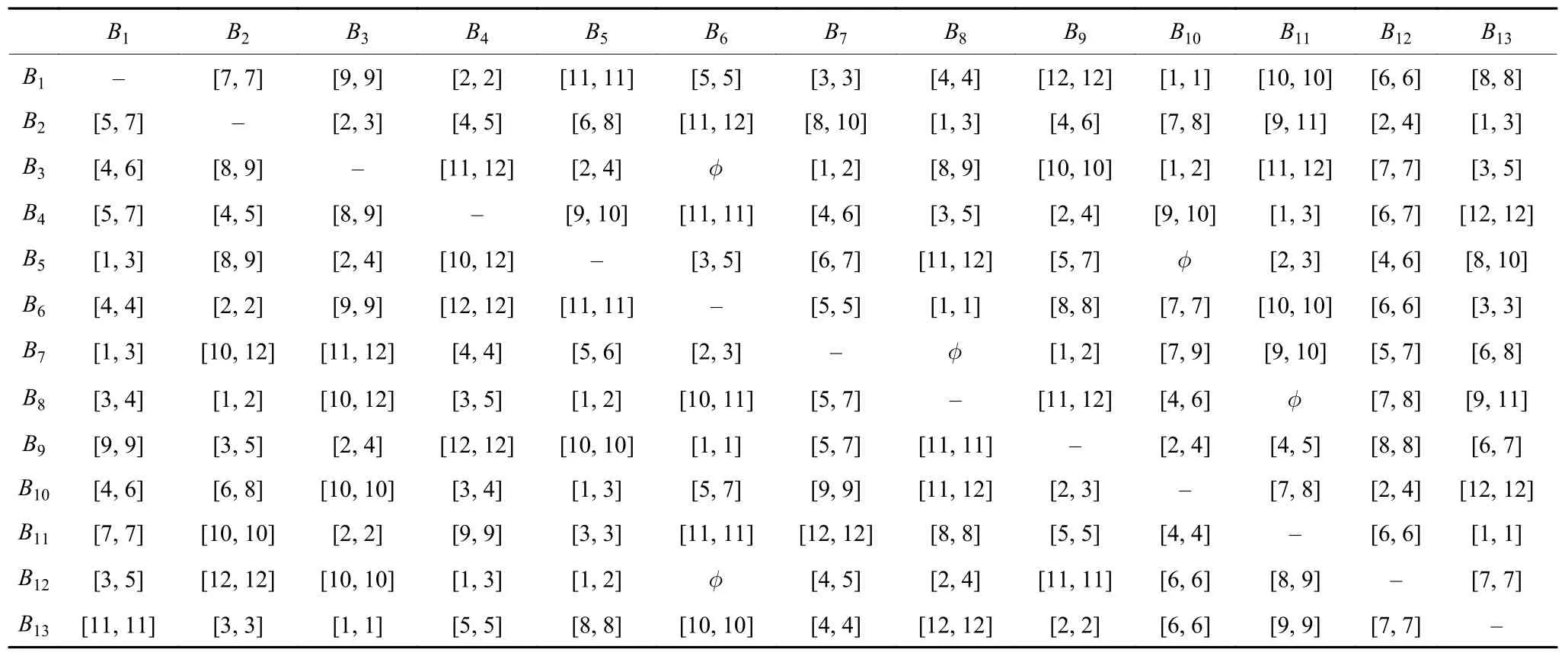
表1 业务员对其他业务员的偏好序信息

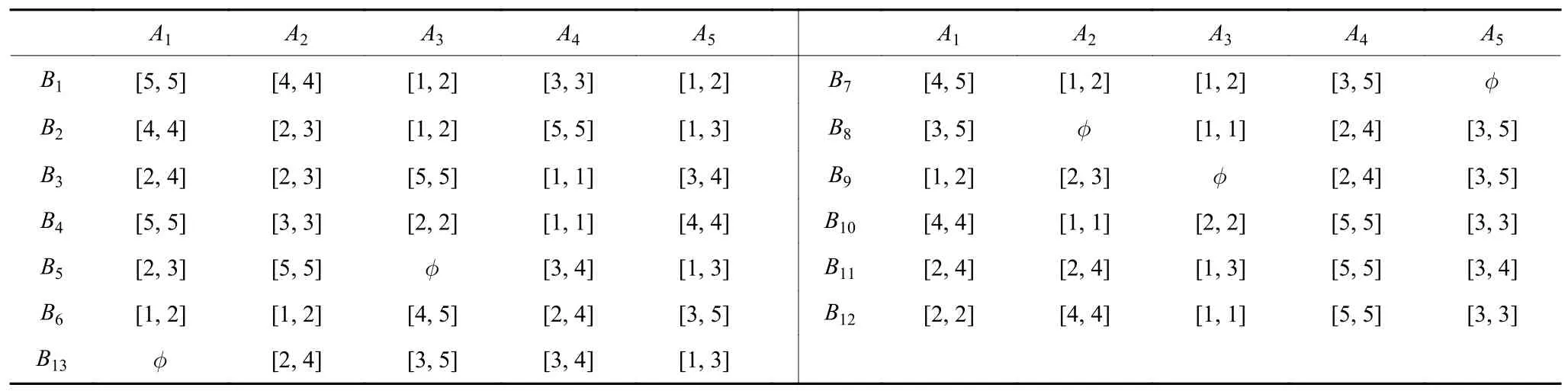
表2 业务员对省区的偏好序信息

表3 省区对业务员的偏好序信息

A4对B6的偏好序为φ，B6对A4偏好序为[2, 4]，首先对不同等级的偏好信息进行统一规范化处理，则A4对B6的偏好排序可以转化为：

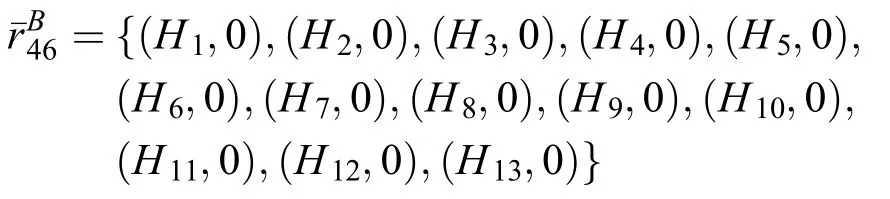
B6对A4偏好排序可以转化为：

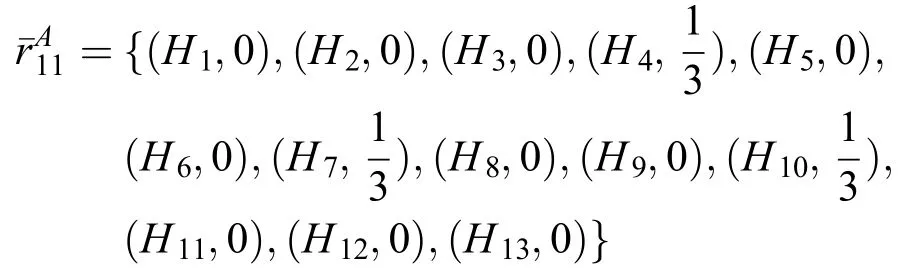
然后对规范后的信息进行证据融合，取wA=0.5，wB=0.5，则：

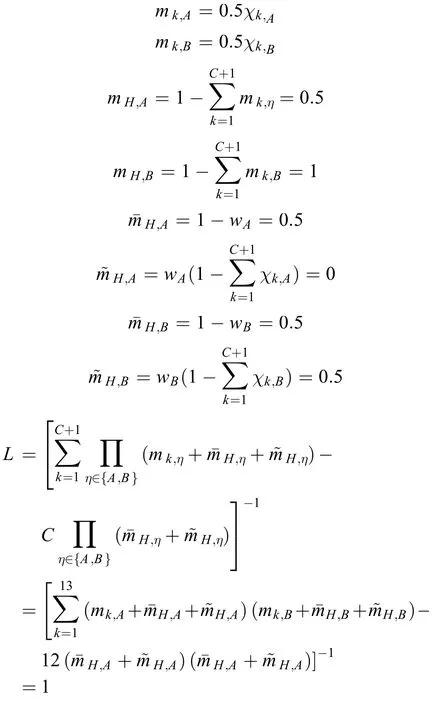
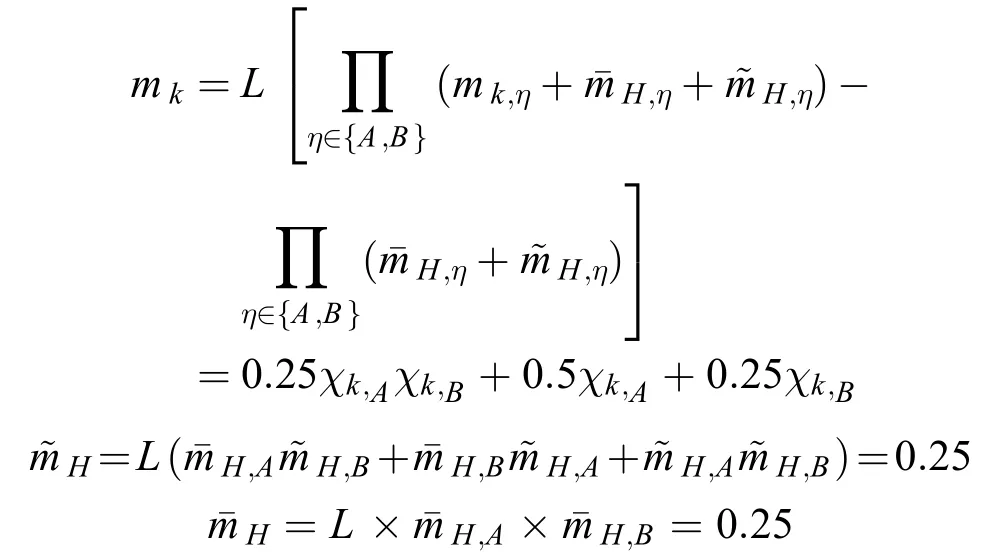
经过证据融合后，得到的项目A4和员工B6融合总信度值为：

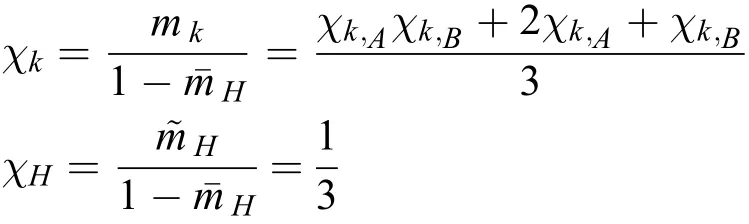
最后，根据上节介绍的三种将融合信度值转化为满意度的方法，则A4对B6的满意度分为以下三种情况：

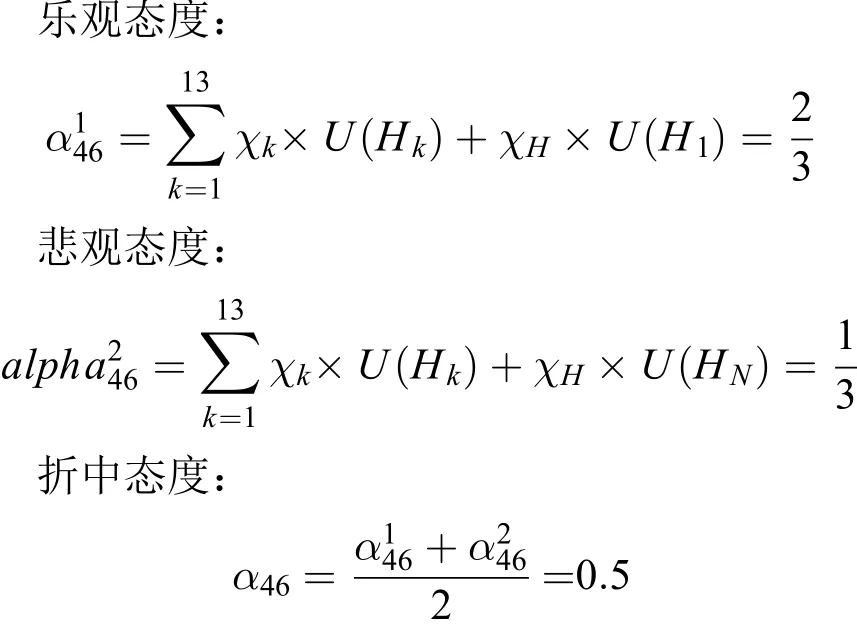
本算例对待不确定信息采用折中的态度，获得融合满意度，如表4、表5所示。

根据业务员与省区的融合满意度和业务员与其他业务员的融合满意度，利用式（18）～式（22）构建并求解业务员与省区的匹配决策模型，可获得最终匹配结果：A1↔B3、A1↔B6、A1↔B13、A2↔B1、A2↔B12、A2↔B7、A3↔B8、A3↔B2、A4↔B10、A4↔B9、A4↔B5A5↔B4、A5↔B11。即：业务员B3、B6、B13与新疆匹配；业务员B1、B12、B7与青海匹配；业务员B8、B2与西藏匹配；业务员B10、B9、B5与甘肃匹配；业务员B4、B11与宁夏匹配。

表4 业务员与省区的融合满意度

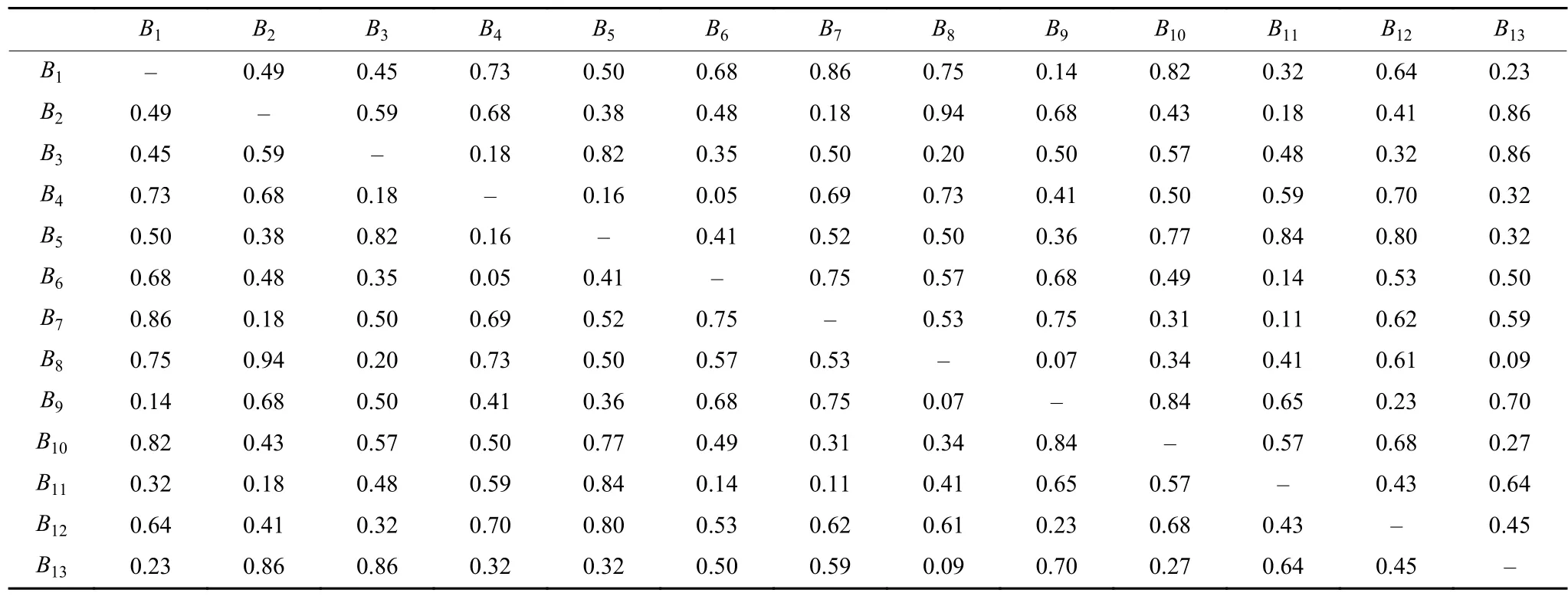
表5 业务员与其他业务员的融合满意度

为说明本文所提方法的可行性和有效性，由于现有文献中考虑主体偏好信息存在不完全或者不确定情形时，对存在缺失偏好的处理方式是对其不匹配，对不确定的偏好信息的处理方式是对其求期望，以期望进一步转化为满意度，现有处理方法将造成信息的缺失。为说明本文所提方法的可行性和有效性，针对上述案例，本文将综合对比一篇同时考虑不完全和不确定偏好信息的文献[17]。首先在文献[17]中，若一方匹配主体给出的关于另一方匹配主体的偏好信息为空集，则判定为该主体与对方是不兼容的，即不能成为匹配对。比如本文算例中B3给出的关于B6的偏好信息为空集，若按照文献[17]中的方法，B3和B6是没有资格成为匹配对的，此方法剥夺了其与对方匹配的权力。而本文所提的方法正是为了弥补以上不足，即使由于个人判断的模糊性或者问题的复杂性，匹配主体有时给出的偏好信息存在缺失，也可以获得与对方匹配的资格。通过本文方法获得的匹配结果如表6所示，B3和B6是可以成为匹配对，可以成为项目组A1的同事的。

其次，利用文献[17]中对不确定偏好信息的转换方式（方法2）计算求解本章的算例，并给出了未考虑同事偏好下的省区-业务员匹配结果求解的匹配结果，与本文所提方法的匹配结果对比如表6所示：从匹配结果可知本文所提方法和未考虑同事偏好的匹配结果不尽相同，说明了同事偏好对最终的匹配结果存在着直接的影响。方法2获得的匹配结果与本文方法获得的匹配结果不尽相同，主要因为在方法2中，计算满意度时，对不确定匹配信息求期望，进一步以期望转化为满意度，这个转化过程中造成部分匹配信息的丢失。如A1对B2给出的偏好排序为[6, 8]，求其期望为7，进一步转化为满意度为0.5，这样等同于A1对B2给出的偏好排序为7，损失了排在第6位和第8位的可能性，因此有可能得不到真正令匹配双方均满意的匹配结果。

表6 两种匹配决策方法的匹配结果

四、结语

本文针对不完全偏好序下考虑同事偏好的项目-员工匹配问题，提出了一种匹配决策方法。首先本文所提方法不仅考虑了项目-员工匹配过程中同事偏好行为对匹配结果的影响，也考虑了偏好序值存在缺失不完全不确定的情况，相比以往匹配决策过程更加符合现实情况；其次本文所提方法在处理不确定信息时保留了不确定信息，减少了不确定信息的丢失；最后本文以证据推理为主要工具，结合决策理论、优化理论等，对不完全偏好序下考虑同事偏好的项目-员工匹配问题进行建模和方法研究，并通过算例验证了方法的可行性和有效性，研究结果可为政府或企业针对现实中的匹配问题提出决策参考。但由于现实环境的复杂性，在获取项目-员工的匹配信息时可能不仅仅是偏好序的形式，也可能存在诸如语言评价值、精确值、直觉模糊数、三角模糊数等多种信息形式。那么能否将该文的研究推广到具有多种信息类型的匹配决策问题中是笔者的一个后续研究方向。

[1] 陈圣群.基于分布式序关系的双边匹配决策方法[J].运筹与管理, 2016, 25(3): 146-150.

[2] GALE D，SHAPLEY L.College admissions and the stability of marriage[J].American Mathematical Monthly, 1962,69(1): 9-15.

[3] HUANG D K, CHIU H N, YEH R H, et al.A fuzzy multi-criteria decision making approach for solving a biobjective personnel assignment problem[J].Computers and Industrial Engineering, 2009, 56(1): 1-10.

[4] 梁海明, 姜艳萍.二手房组合交易匹配决策方法[J].系统工程理论与实践, 2015, 35(2): 358-367.

[5] MINDRUTA D, MOEEN M, AGARWAL R.A twosided matching approach for partner selection and assessing complement arities in partner’s attributes inter-firm alliances[J].Strategic Management Journal, 2016, 37(1): 206-231.

[6] HELLMANN T, PURI M.Venture capital and the professionalization of start-up firm: Empirical evidence[J].Journal of Finance, 2002, 57(1): 169-197.

[7] DUTTA B, MASSÓ J.Stability of Matchings when Individuals Have Preferences Over Colleagues[J].Journal of Economic Theory, 1997, 75(2): 464-475.

[8] ECHENIQUE F, YENMEZ M B.A Solution to Matching with Preferences over Colleagues[J].Games and Economic Behavior, 2007, 59(1): 46-71.

[9] KOMINERS S D.Matching with Preferences over Colleagues Solves Classical Matching[J].Games and Economic Behavior, 2010, 68(2): 773-780.

[10] PYCIA M.Stability and Preference Alignment in Matching and Coalition Formation[J].Econometrica, 2012,80(1): 323-362.

[11] FLANAGAN F.Contracts vs.Preferences over Colleagues in Matching[J].International Journal of Games Theory, 2015, 44(1): 209-223.

[12] IWAMA K, MIYAZAKI S, YAMAUCHI N.A-Approximation Algorithm for the Stable Marriage Problem[J].Algorithmica, 2005, 51(3): 342-356.

[13] LIU Q, MAILATH G J, POSTLEWAITE A, et al.Stable matching with incomplete information[J].Econometrica,2014, 82(2): 541-587.

[14] KNOBLAUCH V.Marriage matching and gender satisfaction[J].Social Choice and Welfare, 2009, 32(1): 15-27.

[15] 乐琦, 樊治平.具有不确定偏好序信息的双边匹配决策问题研究[J].运筹与管理, 2012, 21(1): 57-63.

[16] 乐琦, 樊治平.基于不完全序值信息的双边匹配决策方法[J].管理科学学报, 2015, 18(2): 23-35.

[17] 乐琦, 王中兴, 李健.不完全不确定序数信息下的双边匹配决策[J].模糊系统与数学, 2015, 29(2): 118-124.

[18] 乐琦, 张磊, 张莉莉.不确定偏好序信息下考虑主体心理行为的双边匹配决策方法[J].运筹与管理, 2015, 24(4):113-120.

[19] WANG Y M, YANG J B, XU D L.Environmental impact assessment using the evidential reasoning approach[J].European Journal of Operational Research, 2006, 174(3): 1885-1913.

[20] YANG J B, WANG Y M, XU D L, et al.The evidential reasoning approach for MADA under both probabilistic and fuzzy uncertainties[J].European Journal of Operational Research, 2006, 171(1): 309-343.

编 辑 何婧

A Study on Project-Employee Matching Decision Considering Colleagues Preferences Under Incomplete Preference Ordering Information

SUN Chao-yuan DONG Zhan-ying
(University of Electronic Science and Technology of China Chengdu 611731 China)

A matching decision method considering colleagues preferences relation is proposed to solve the project-employee matching decision problems with incomplete ordering information.Firstly, the incomplete ordering information given by matching agents is transformed into rank belief degrees.Secondly, two-sided rank belief degrees are taken as pieces of evidence and the fusion degrees of projects-employees and employee-other employees are got by evidence fusion.Furthermore, fusion degrees are transformed into the satisfaction degrees,then an optimization model is constructed and solved considering colleagues preferences relation, where the two objectives are to maximize projects-employees’ satisfaction degrees and maximize the employee-other employees’satisfaction degrees.Finally, a numerical example illustrates the feasibility and effectiveness of the proposed method.

Colleagues preferences; matching decision; incomplete preference ordering; evidential reasoning

C934

A

10.14071/j.1008-8105(2017)06-0093-08

2017-03-08

国家自然科学基金项目（71571032）.

孙朝苑（1976-）女，博士，电子科技大学经济与管理学院副教授、硕士生导师；董战英（1991-）女，电子科技大学经济与管理学院硕士研究生.