基于小波变换和AR模型的脑电信号注意力状态识别

翟延祥，薄 华

(上海海事大学 信息工程学院院，上海 201306)

基于小波变换和AR模型的脑电信号注意力状态识别

翟延祥，薄 华

(上海海事大学 信息工程学院院，上海201306)

针对神经反馈训练研究中注意力状态识别精度不高的特点，建立了一种基于离散小波变换和AR模型的方法用于提高注意力识别的精度。利用dbN小波函数对脑电数据样本进行多层小波分解，提取小波变换系数的三种统计特征；同时采用Brug算法得到AR模型系数；用这两种参数相结合后使用支持向量机进行识别。与只采用小波变换或AR模型等特征提取方法相比，本文方法有更高的识别率。

注意力识别；小波变换；AR模型；支持向量机

0 引言

脑电信号(ElectroEncephaloGram,EEG)产生于大脑皮层的神经活动，它是采用非侵入式方式记录从头皮采集到的大脑皮层信号，一定程度上反映了大脑活动状态[1]。脑电注意力状态识别是脑电生物反馈的重要组成部分，在临床医疗方面有着许多的应用，比如治疗注意缺陷多动障碍(Attention Deficit Hyperactive Disorder,ADHD)、自闭症(Autistic Specturm Disorder,ASD)、癫痫等。

目前采用频谱分析方法识别大脑状态的注意水平主要有两种算法，一种是计算θ/β比率得出大脑注意水平状态；另一种是将脑电信号分解为δ波(≤4 Hz)、θ波(4～8 Hz)、α波(8～15 Hz)、β波(12～30 Hz)和其他波(≥30 Hz)，把每个波段的能量或者功率谱作为反馈信息，比如维格纳-费利分布、匹配追踪法等[2]。然而脑电属于非线性随机信号，仅仅采用脑电的频谱特征并不能完全真实地反映实际状况，从而影响训练效果。因此本文利用小波低频变化缓慢、高频变化较快的特点提出一种将离散小波系数和AR模型系数两者相结合的特征提取方法。将采集数据小波分解至7层，提取与注意力有关的4种波段。将小波系数的能量均值、方差、均值与8阶AR模型系数用作支持向量机的输入。

1 小波变换和AR建模

1.1小波变换

信号f(t)的连续小波(Continuous Wavelet Transform, CWT)变换[3]定义为：

(1)

连续小波变化就是由小波基函数Ψτ,a(t)做平移尺度变换得到的一种分析方法。其中a为尺度因子，τ为平移因子。当a增大时(agt;1)，表示用伸展的Ψ(t)去观察整个f(t)；反之当a减小时(alt;1)，表示用压缩的Ψ(t)去观察整个f(t)的局部。尽管连续小波变换具有自动调节信号的带宽等一系列优点，但其计算复杂、冗余性大，因此常采用Mallat快速算法。

(2)

其中⊕表示直和。如果原始信号x(t)的信号空间为V0，首先V0被分解为相互独立的V1和高频空间W1,第j步时将Vj-1分解为类似低频空间Vj和高频空间Wj，其本质就是划分空间。

Mallat的算法表达如下：

(1)分解算法

根据不同的尺度把原始信号分解为细节信号与逼近信号，其分解过程如图1所示。

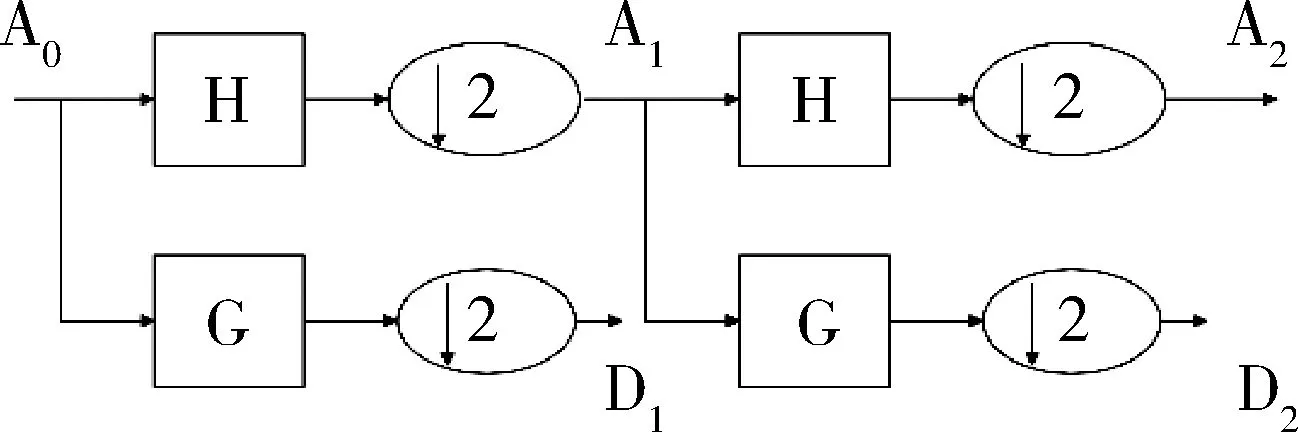
图1 Mallat算法分解过程

(2)重建算法

重建算法就是分解算法的逆过程，其核心就是由分解后的细节与逼近信号相结合还原为初始信号，如图2所示。

图3 7级小波分解

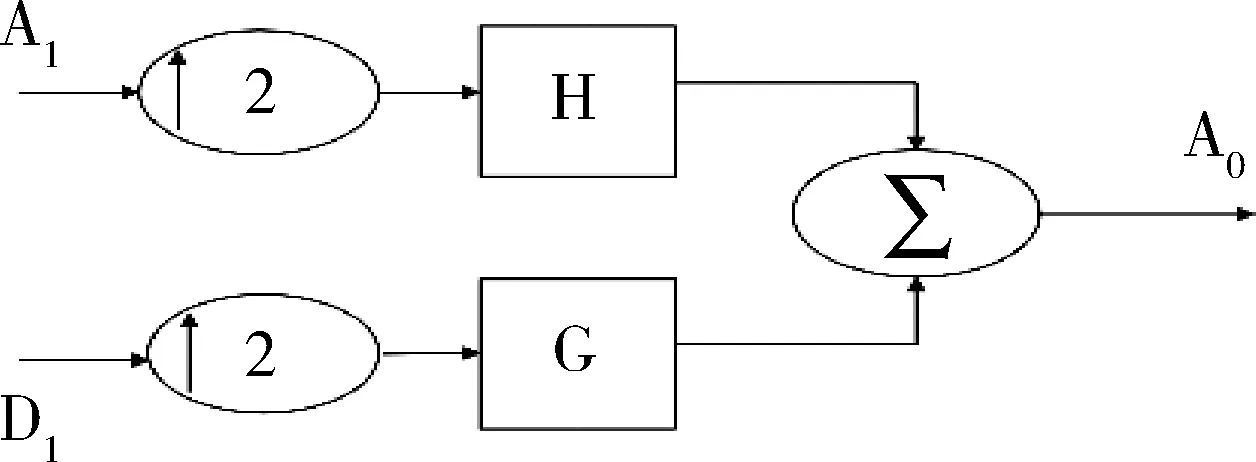
图2 Mallat算法重建过程

1.2AR模型

自回归模型(Auto Regressive Model,AR)[4]是一种线性组合了前期若干时刻的随机变量来描述后期某段时刻随机变量的线形回归模型，本质是一种线形预测，表示如下：

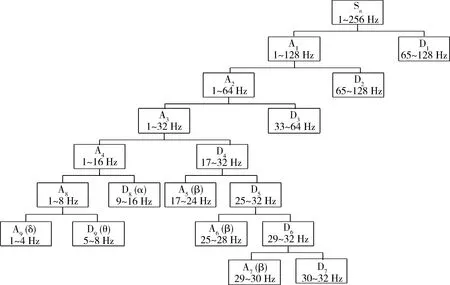
图4 原始脑电信号

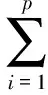
(3)

其中ε(n)是方差为σ2，均值为零的白噪声序列，p表示AR模型的阶数。因此脑电信号序列x(n)可以看作白噪声序列ε(n)通过AR模型H(z)的输出。建立AR模型时，首要问题就是阶数为多少时比较合适。模型的阶数在递推过程中实现，使用Levinson-Durbin递推方法时，可以给出低阶到高阶的每一组参数，当模型的最小预测误差功率P不再发生变化时，即是所需要的正确阶数。文献[5]以及实验表明脑电处理效果最好的模型阶数为6～8。在采用Brug算法求解8阶AR模型系数的之前，需要通过适当的变换去掉不平稳的趋势得到平稳、服从正态分布的平稳时间序列。

2 支持向量机

本文把小波7层分解后得到α、β、θ、δ四个波段，小波变换系数各有三种统计特征加上提取的8阶AR模型系数共计20个特征值作为SVM的输入。此次采集的样本数据共160组，将其中存在明显漂移较大的15组数据去除后，选取120组作为训练样本，另外的25组作为测试样本。SVM的核函数的选择是首要考虑的问题，这里选用线形核函数。然后利用训练样本计算SVM的参数(如拉格朗日乘子a，具有超平面的发向量w和偏置b等)并确定判别函数f(x),最后输入测试样本，根据sgn(f(x))的值输出类别，如果sgn(f(x))为1，则为注意力脑电信号；如果为-1，则为非注意力脑电信号。

3 脑电特征向量的提取

根据上述小波分解的原理和步骤，对原始脑电信号采用Mallat快速算法，用db4小波进行7层分解。其小波分解过程如图3所示。Sn表示待分解的原始信号。其中An(n=1,2,3…)表示分解后得到的低频部分即逼近信号;Dn(n=1,2,3…)表示高频部分即细节信号。

图4为实验中记录到的4 s时间内FP1通道的注意和非注意状态的脑电信号。

注意力脑电信号分解时，随着分解层数的增加，各节点信号的范围逐渐缩小，也更容易得到所需的信号。本文采集仪器的采样频率为512 Hz，将信号分解到第6层发现肌电干扰信号主要分布在D3(频率33～64 Hz),脑电β节律表现在尺度A5、A6、A7(频率17～24 Hz，25～28 Hz，29～30 Hz)中，α节律集中在尺度D8中(频率8.9～15.6 Hz)，θ节律集中在尺度D9(频率4.8～8.2 Hz)中，δ节律集中在尺度A8上(频率1～4 Hz)。通过多分辨小波将原始信号分解到不同频带上，本文选取A5、A6、A7、D8、A9、D9以做进一步研究。为了计算方便，此处将同属于β波形的A5、A6、A7合并。

图5表示提取到的四种脑电波形，图6为各节律对应的频谱。

图5 小波提取的四种分量

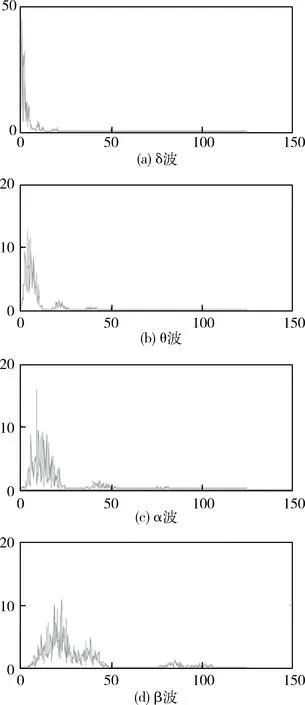
图6 对应的频谱图

由图5、图6可知，小波分解提取的与注意力有关的四种波形效果较好，为了提高识别精度，本文提取了小波系数的能量均值、均方差、均值作为特征向量。

本文另一部分特征向量的获得是采用8阶AR模型提取的8个系数。常用的AR模型的系数求解法有自相关法、Brug算法以及改进的协方差法等。由于Brug算法是令前后向预测误差功率之和ρfb为最小，此处采用Brug算法。

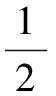
(3)

前向预测误差ρf和后向预测误差ρb的求和范围是ρ～N-1，这时有：

(4)

(5)

Brug算法又叫最大熵法(MEM)，它是通过最大化观测序列的熵与改进的协方差方法相比求解AR模型的过程，具有相当稳定且分辨率较高的优点。此处选取0～8 s之间的脑电数据，每隔0.4 s做一次AR功率谱估计，并将这0.4 s内的功率谱相加得到20个数据，如图7和图8所示。

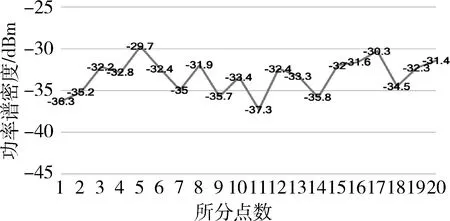
图7 非注意状态的功率谱密度

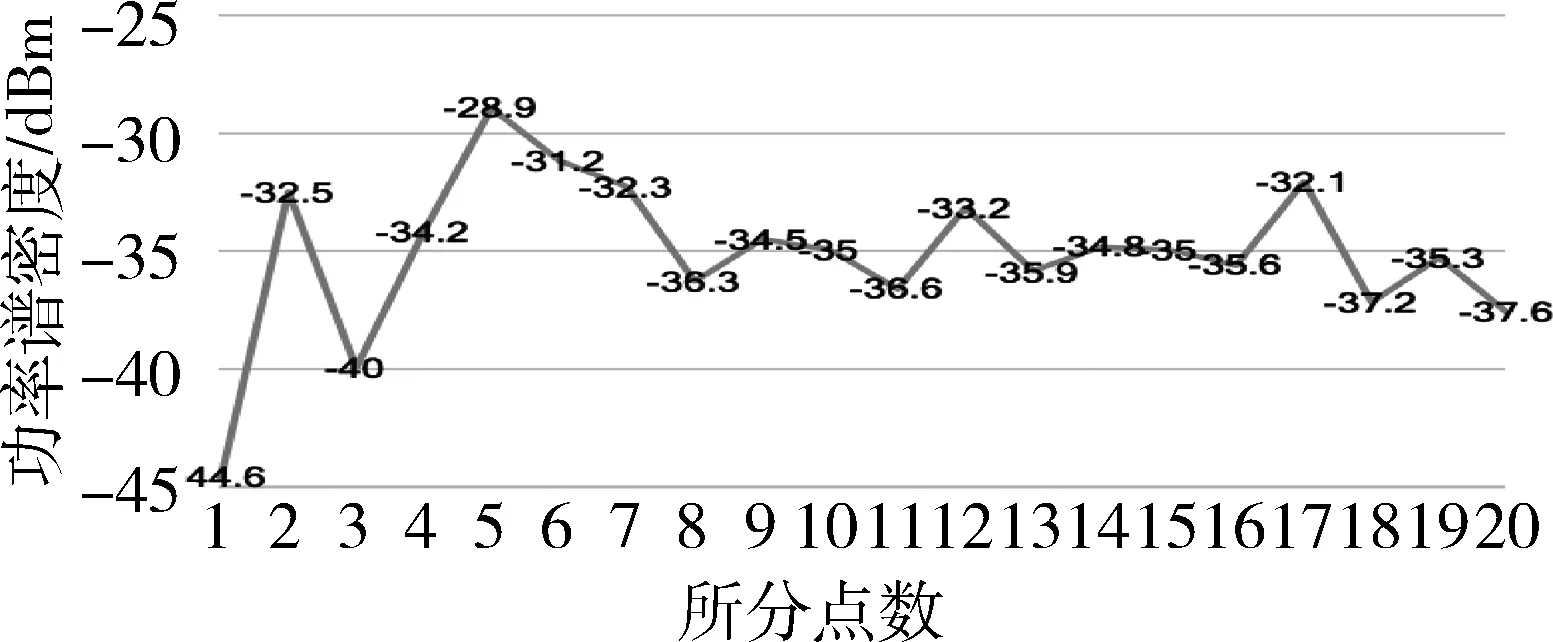
图8 注意状态的功率谱密度

4 实验设计

为了确保上述方法的有效性，本文设计如下实验采集不同状态的注意力脑电信号作为数据样本。实验选取的受试者为16名健康的研究生，8男8女，年龄在 24～28 岁之间，右利手，均在头脑清醒，头皮和额头被清洁过的情况下接受测试。测试前，用酒精清洁仪器电级，受试者坐于一个较为舒适的带靠背的椅子上，心情愉悦放松，无任何肌肉紧张与运动。

(1)非注意任务。受试者坐在电脑前，安静地观望屏幕，使自己处于放松状态，屏幕上呈现游戏画面。

(2)注意任务。受试者进行贪吃蛇的游戏，不小心结束游戏了则重新开始，时间为3 min。

贪吃蛇是一种休闲益智类手机游戏，该游戏通过控制舌头方向吃蛋，从而使自己变长，其中不能碰到其他蛇、墙壁，也不能碰到自己的身体，总的来说，非常有利于集中注意力。

本文采用美国神念公司生产的脑电采集装置，采集点放在Fp1电极处，采样率为512 Hz，在进行特征提取之前，首先对数据进行一些必要的预处理。比如去除眼电(EOG)和工频干扰信号，将采集后的数据通过一个低通滤波器，过滤掉大于50 Hz的其他工频干扰。为了解决EEG信号异常更正，对由受试者采集的原始EEG样本点，把大于样本均值95%的点或小于样本均值5%的点分别用样本均值乘以0.95及样本均值乘以0.05替代，完成异常点更正。为了进行更好的分类，尽量选取较多的数据段，从每个被试者采集到的信号中截取5段长度为4 s的数据段，即每段长度为2 048个点，16个被试者每人每类截取5段长度，得到16×5=80个注意状态数据段和16×5=80个非注意状态数据段，数据集合的尺寸为2 048×160。

5 实验结果

通过观察采集到的160组数据，将其中存在明显漂移状况的15组数据去除。选取75组作为训练样本，另外的70组作为测试样本。此处把小波7层分解后得到α，β，θ，δ四种波段，小波变换系数各有三种统计特征，加上提取的8阶AR模型系数共计20个特征值作为SVM的输入。用SVM进行脑电注意力识别时，先由训练样本求出Lagrange乘子a，偏置值b，再确定判别函数f(x)。然后根据测试样本确定sgn(f(x)的值，若sgn(f(x)为1，则为注意力状态，若sgn(f(x)为-1，则为非注意力状态，为确保实验准确性，多次重复实验，分类结果如表1所示。

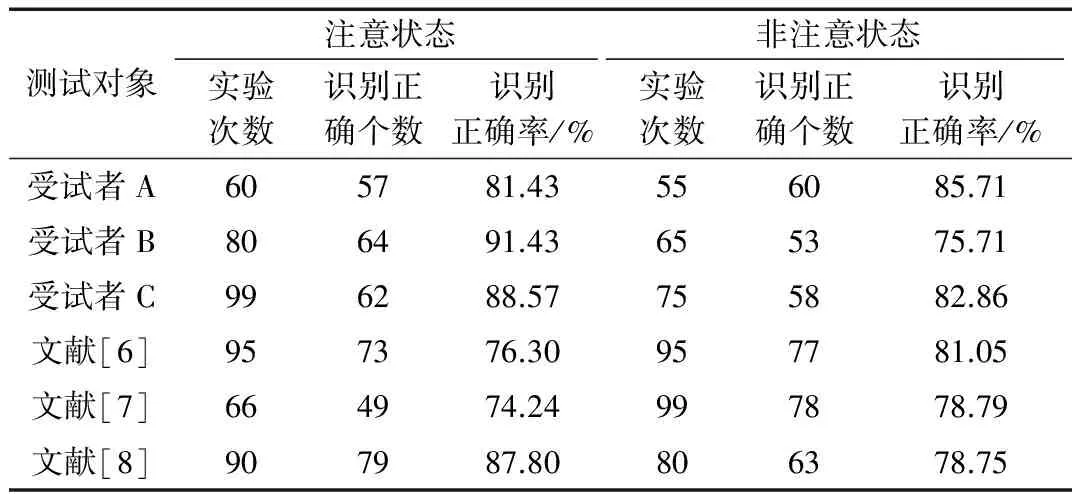
表1 采用SVM注意力分类结果

从表1中可以看出，采用文献[6]和文献[7]测试的小波变换和AR模型方法的最高正确识别率仅有82.20%和75%，而本文提出的小波变化和AR模型相结合的方法得到的最高识别率可达91.43%，远高于单独的分析方法。同时与文献[8]中提出的改进的样本熵方法相比优势也较为明显，其正确识别率为87.80%。因此，在神经反馈训练研究中，本文提出的特征提取方法由于较好的正确识别率可作进一步研究。

6 结论

本文通过结合小波变换系数和AR模型的方法提高了注意力状态的识别精度。然而不可避免地会存在一些不足，希望能在未来的研究中能做进一步的改进:

(1)设计实验时可以调整受试者的男女比例，年龄分布以及适当的增加人数。数据采集时测试者所处环境的声音干扰以及集中程度都会造成很大影响，应尽量避免。

(2)脑电信号属于非线性非平稳信号，节律多，随机性强。目前为止，人类对脑电信号的探索从目视观察到时域、频域分析以及非线性分析，对其认识也更加深刻。对于脑电信号的分析还有许多其他分析方法，譬如动力学分析、因果性分析以及同步性分析等，在下一步做进一步研究。

[1] NUNEZ P L,SRINIVASAN R. Electric fields of the brain[M].New York:Oxford University Press,2006.

[2] 白东梅.脑电信号的特性分析与特征提取[D].大连：大连理工大学，2006.

[3] 小波分析在图像降噪中的应用[J].微型机与应用，2013，32(12)：68-70.

[4] 张德丰.MATLAB 小波分析[M].北京：机械工业出版社，2009.

[5] 胡广树.数学信号处理：理论、算法与实践[M].北京：清华大学出版社，2003.

[6] 李颖洁 ，邱意弘.脑电信号分析方法及器应用[M].北京：科学出版社，2009.

[7] 徐爱国，宋爱国.单次运动想象脑电的特征提取和分类[J].东南大学学报(自然科学版)，2011，39(s2):103-106.

[8] 周鹏，葛家怡，曹红宝，等，基于样本熵的运动想象分类研究[J].信息与控制，2008，37(2):191-196.

2017-04-25)

翟延祥(1992-)，男，硕士，主要研究方向：模式识别，信号处理。

薄华(1971-)，女，博士，副教授，主要研究方向：模式识别，机器学习。

Attention state recognition of EEG based on wavelet transform and AR model

Zhai Yanxiang, Bo Hua

( College of Information Engineering, Shanghai Maritime University, Shanghai 201306, China)

As the accuracy of attention state recognition is not high in neural feedback training, this paper established a method based on discrete wavelet transform and AR model to improve the accuracy of attention state recognition. This paper uses dbN wavelet function to do EEG data samples multi-layer wavelet decomposition and extract three kinds of statistical characteristics of wavelet transform coefficients. At the same time it adops Brug algorithms to get AR model coefficient. By combining these two kinds of parameters, it uses Support Vector Machine (SVM) for identification. Compared to the feature extraction methods which only use the wavelet transform and AR model, the method proposed in this paper has higher recognition rate.

attention state recognition; wavelet transform; Auto Regressive model; Support Vector Mache (SVM)

TP212.3

A

10.19358/j.issn.1674- 7720.2017.22.024

翟延祥，薄华.基于小波变换和AR模型的脑电信号注意力状态识别J.微型机与应用，2017,36(22)：91-94，98.