一种用于确定配电系统中多个谐波源位置的新方法

张 翠，党幼云，罗 辉，董 潭，李婧瑄

(西安工程大学 电子信息学院，陕西 西安 710048)

一种用于确定配电系统中多个谐波源位置的新方法

张 翠，党幼云，罗 辉，董 潭，李婧瑄

(西安工程大学 电子信息学院，陕西 西安710048)

基于独立分量分析和互信息理论，研究了确定分布系统中多重谐波源位置的技术。独立分量分析用于估计由谐波源引起的注入谐波电流的分布，互信息理论用于估计谐波源的位置。为了验证此种方法的准确性，在IEEE34总线、IEEE30总线、IEEE33径向分布系统中做了仿真，定位多个谐波源进行了数值模拟。结果表明，所采用的方法可以准确地估计多个谐波源的位置，而无需事先知道网络参数，为达到谐波治理、有效分清谐波责任提供依据。

多重谐波源位置；独立分量分析；互信息理论

0 引言

电力系统中的谐波源定位是用于解决在电力系统中谐波失真的客户和公用事业之间的责任归属的方法之一。在文献中可以找到不同的单点定位方法，用于定位谐波源并且确定在PCC处的效应和客户谐波失真的份额[1-4]。所有这些方法都集中解决在PCC处谐波源定位的单节点策略，这样的方法在实际系统中不能工作，因为谐波源存在并且在电力网络中的各个节点处传播[5-7]，因此，提出了在分布系统中定位多个谐波源的几种方法。

在文献[8]中，独立分量分析(ICA)已被应用于定位多个谐波源。在该方法中，由测量放置技术确定总线处的测量电压，估计系统的阻抗矩阵和谐波源的电流迹线，然后获得估计的阻抗矩阵和实际阻抗矩阵之间的最小电距离，用于估计谐波源的位置。然而，该方法不是完全实用的，因为它需要确定系统在每个谐波频率处的实际阻抗矩阵。因此采用一种基于ICA和互信息(MI)理论的新方法，以识别分布系统中多重谐波源的位置。在该方法中，ICA用于重建或估计由谐波源产生的谐波电流，而MI理论用于确定谐波源的位置。与先前的方法不同，在该方法中，仅在所有总线处进行电压测量，并且不需要测量有功和无功功率等其他参数。本文在MATLAB环境中对存在多个谐波源的IEEE-34母线网络进行了仿真。仿真结果表明这种方法精度高。

1 独立分量分析

基本上，ICA是将观察到的信号线性变换为彼此独立的源信号的技术。为了将源信号与观测信号分离，考虑了某些假设，使得独立分量在统计学上是独立的，源信号必须具有非正弦分布，并且观测值的数量应该大于或等于信号源的数量[9]。假设有N个源和M个测量，线性混合模型的ICA可以写成：

xj=aj1s1+aj2s2+…+ajnsn

(1)

对于所有j=1,2,…,M，式(1)的矩阵表示为:

X=AS

(2)

N维未知的源信号：S(t)=[s1(t),s2(t),…,sn(t)]T。

M维观测信号：X(t)=[x1(t),x2(t),…,xm(t)]T。

其中A为m×n维混叠矩阵，X和S是M×T和N×T矩阵，其列向量是观察信号和源信号，T是观察的数量。ICA的目标是从可用中找到S和A的估计观察X。 未知源矩阵S可以是：

Sest=WX

(3)

其中：Sest是具有n×t维的源信号S的估计；W是m×n维分离矩阵，是混叠矩阵A的逆矩阵。

应用源信号非离散性最大化的ICA算法[10]估计由式(3)给出的ICA模型表示。 基于该方法，考虑随机变量观察信号与源信号信息相关的熵。

为了确定独立分量，最大化负熵是必要的。

通过最大化N个单位对比度函数的和并考虑相关的约束，获得如下的优化问题：

(4)

其中Wi(i=1,2,…,N)是分离矩阵的行，W是系数矩阵A的逆。

应用FastICA算法[11]最大化式(4)所示的对比度函数。通过ICA中心化[9]观察向量X。通过中心化，向量X的平均值被减去，并且均值变量通过白化被变换为零；观察到的向量X被线性变换地映射到新的向量X，其中它的分量是不相关的，并且它们的方差等于1。在白化中，认为

(5)

其中D和E分别是从观察向量的协方差矩阵X获得的特征值的对角矩阵和特征向量的正交矩阵[12]。

2 相互信息理论

受信息理论的启发，另一种用于ICA估计的方法是MI的最小化。用熵的概念导出熵的离散形式：

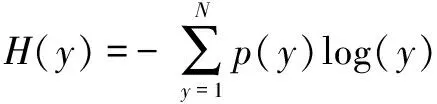
(6)

式(6)中的熵可以解释为具有概率函数p的事件其不确定性的度量。 事实上，随机变量的熵可以定义为观察变量给出的信息。 在B发生的试验的后续过程中,使用条件熵[13],确定变量的不确定性。假设随机变量A和B由N元素组成ai和bi，对于i=1,2,…,N，条件熵可以定义为：

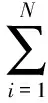
(7)

假设B是H(A|bi)的平均值，可以写入变量A和B的条件熵如：

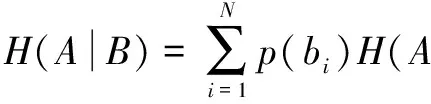
(8)

变量A和B的互信息I为：

I(A,B)=H(A)-H(AB),I(A,B)≥0

(9)

式(9)是对称的，并且可以被解释为关于包含在B中的A的信息，反之亦然。如果式(4)中W是独立的，它们的MI将为零[14]。此外，MI是更好的测量两个随机变量相关性的函数，而不是相关函数[15]。原因是MI能够测量两个变量之间的一般依赖性，而相关函数式(4)只能测量它们之间的线性相关性。

3 ICA和互信息在谐波源定位理论的应用

本节描述了估计多个谐波源位置的过程。首先，考虑非正弦条件下的系统方程，其矩阵形式写成：

Vh=ZhIh

(10)

其中V、Z和I是总线电压、阻抗和总线注入的电流矢量，h是谐波次数。如果电压V和阻抗Z是已知的，则谐波电流I可以使用式(10)求解。应用式(10)到ICA，混叠矩阵A表示在谐波域中的导纳矩阵Z的估计信号，S表示注入总线的电流矢量，X表示测量的谐波电压矢量。由式(10)得，各个总线处的谐波源产生的注入谐波电流与总线电压之间具有关系。通过使用MI理论，在每个总线处产生的谐波电流具有总线电压的最大MI，并且由于分支之间的电流分割，这些谐波电流和其他总线电压之间的MI减小。

使用ICA和MI理论来实现估计多个谐波源位置的步骤如下：

(1)确定所有总线的谐波电压；

(2)使用快速ICA算法来重构谐波源的电流轨迹；

(3)计算提取的电流轨迹和总线电压之间的熵；

(4)根据计算的MI确定谐波源的位置。

4 仿真结果

为了验证这种方法的准确性，选择IEEE 34总线径向分布系统作为测试系统[16]。如图1所示，测试系统含有在总线15,25和33处的第5，第7和第11次谐波阶的三个谐波源。假设所有负载具有恒定的功率因数，并且谐波负载建模为具有在文献[17]中给出的频谱的谐波电流注入源。

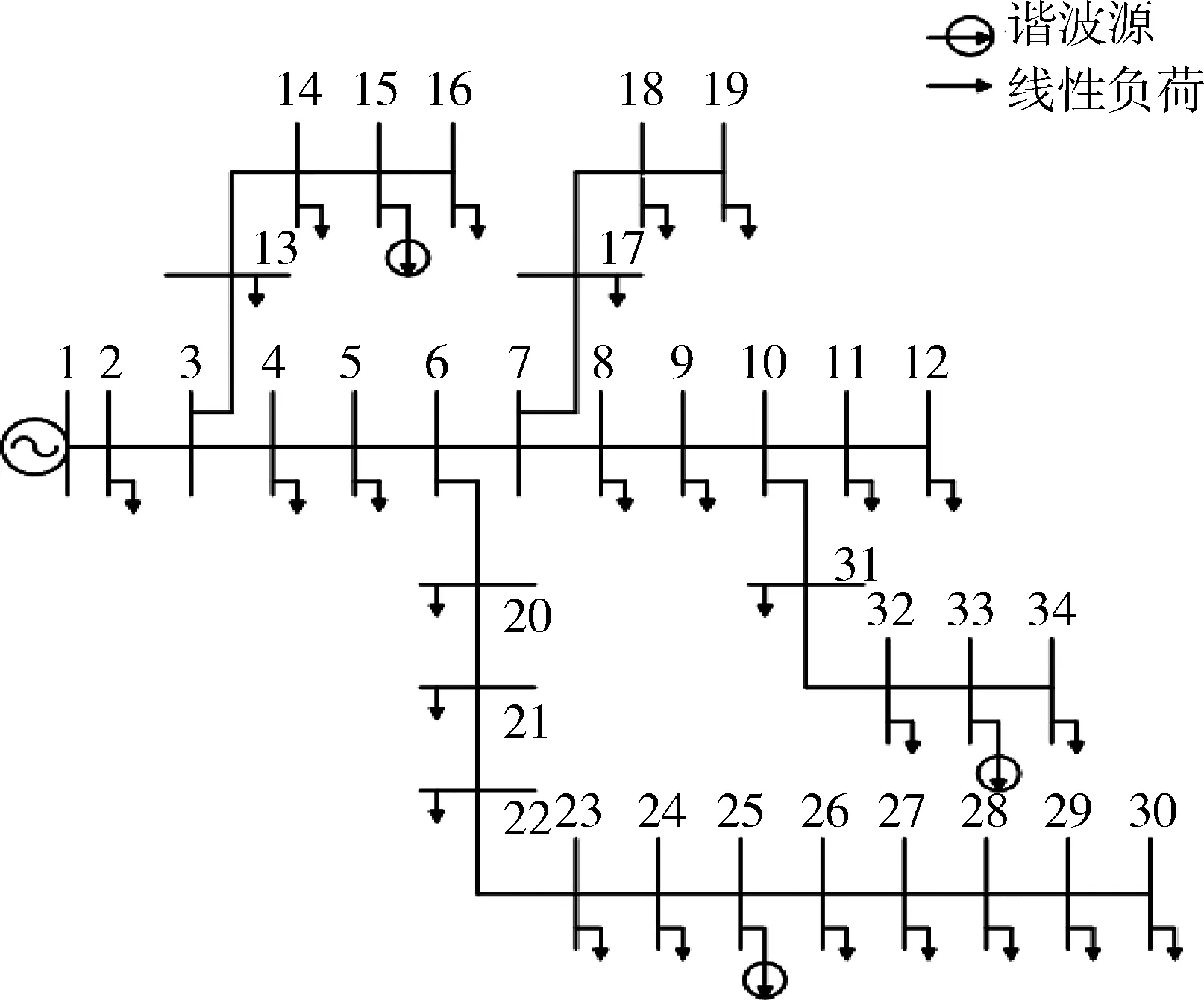
图1 IEEE 34总线测试系统

在用ICA估计多个谐波源之前，使用模拟谐波功率流和产生谐波电压的MATLAB代码对文献[18-19]中引入的径向系统的谐波负载流算法进行编程。通过求解式(10)中的线性系统方程，计算谐波总线电压每个感兴趣的谐波频率。在这里，为34个总线中的每一个创建了500个电压样本以确定谐波测量向量X。在MATLAB中将快速ICA算法用于重建由总线15、25和33处的谐波源产生的谐波电流。

为了验证提取谐波电流轨迹的ICA算法的精度，计算了实际和重建的电流信号之间的相关系数，如表1所示。从该表中可以看出，所有相关系数都在可接受范围，因为它们的值都接近于1。这意味着估计的和实际的谐波电流之间的高精度的匹配。表2给出了信号的均方误差，以便量化估计的和实际的谐波电流之间的差。表2的结果表明，快速ICA算法可以重建具有高精度的信号，其中估计的和实际的谐波电流的均方误差小于0.002。为了具有较小的均方误差和在相关系数结果中实现更好的精度，可以通过增加采样数量或采样时间来提高ICA算法的性能[20]。

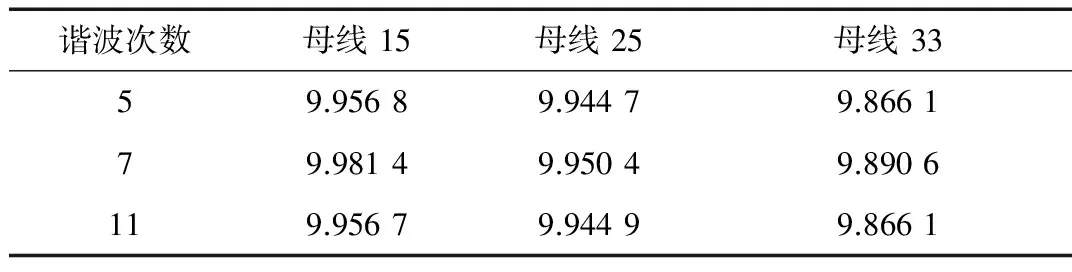
表1 实际和重建信号之间的相关系数

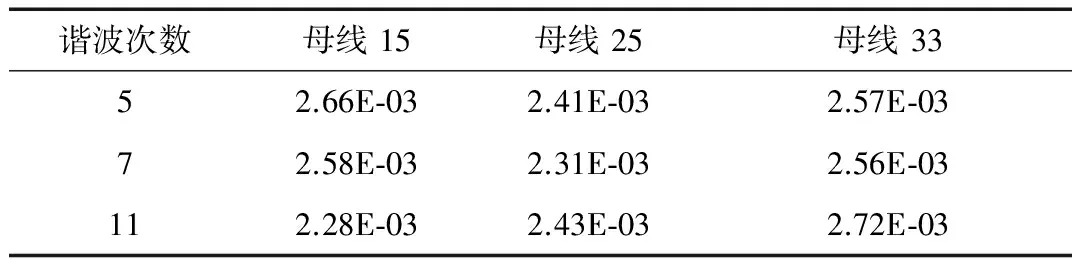
表2 实际和重建信号之间的平均误差

为了识别谐波源的位置，应用MI理论计算出各次谐波的估计电流趋势和总线电压之间的成对MI。MI的结果如表3所示，其中每一列和行分别表示各次谐波的估计电流和谐波总线电压。每列和行之间的交叉表示在各次谐波处的三个估计电流与指定的总线谐波电压之间的MI。

如表3所示，粗略MI值意味着相关总线在估计的谐波电流和电压之间具有最大的MI，因此该总线被识别为谐波源的位置。例如，在第5谐波阶(第一列)的第一估计电流和总线25(第25行)的谐波电压对应的MI为2.45，MI在相关列中具有最大值。这意味着谐波源的位置在总线25处。从表中可以看出，谐波源位置位于总线15、25和33，因为MI值在这些总线处为高，因此，通过使用ICA和MI理论所提出的方法正确地识别了总线15、25和33处的谐波源位置。

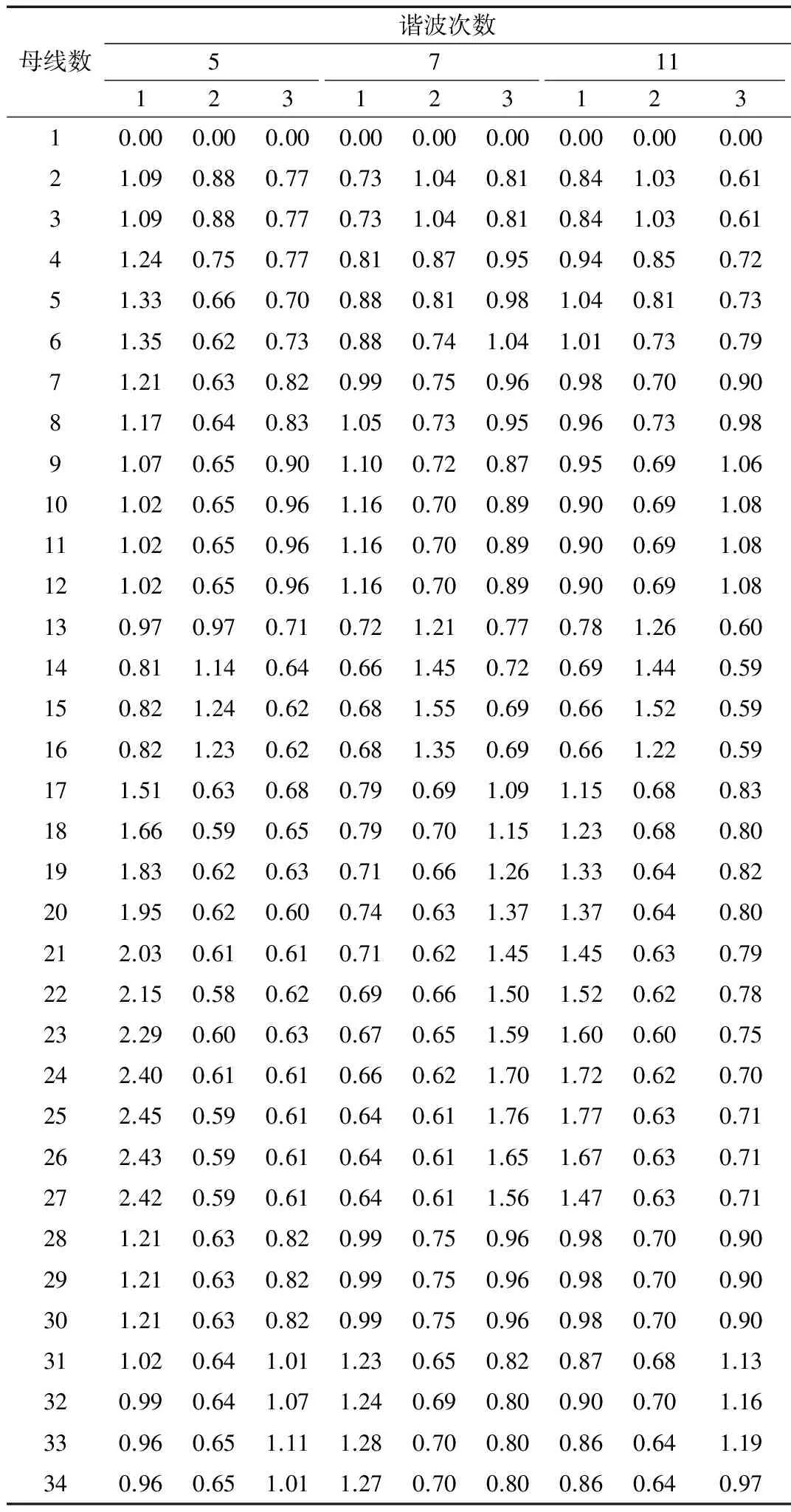
表3 估计电流和总线之间的相互信息电压

5 结论

一种使用ICA和MI理论在分布系统中定位多个谐波源的新技术得到验证。在所提出的方法中，作为盲源分离技术的ICA用于估计由谐波源产生的注入谐波电流，并且MI理论用于识别谐波源的位置。从案例研究的结果证实，所提出的方法可以准确地识别多谐波源在34总线径向分布系统中的位置。为了更准确地进行验证，在IEEE 30总线分布和IEEE 33总线分布系统做了仿真，验证此方法准确性很高。此方法能进行多重谐波源定位。

[1] 孙媛媛,李培鑫,尹志明.基于门限电压法的谐波源定位[J].电力系统自动化,2015,39(23):145-151.

[2] 尹懿.光电传感器式焊缝自动跟踪系统的研究[D].湘潭：湘潭大学,2004.

[3] 王守相,张颖,韩亮.配电系统三相不确定谐波潮流的复仿射计算方法[J].电力系统自动化,2015,39(7):41-46.

[4] 陈双燕.低压单相非线负荷谐波特性的实验研究[D].重庆：重庆大学,2010.

[5] 李湘.配电网多谐波源识别方法的研究[D].重庆：重庆大学,2014.

[6] 韩美玉.电力系统谐波状态估计与谐波源定位技术研究[D].北京：中国石油大学,2011.

[7] 孙媛媛.非线性电力电子装置的谐波源模型及其在谐波分析中的应用[D].济南：山东大学,2009.

[8] 郑东方,陈红坤,杨志平.独立分量分析在谐波源辨识中的应用[J].电力系统及其自动化,2012,24(4):139-144.

[9] 郑春厚.独立分量分析算法及其应用研究[D].合肥：中国科学技术大学,2006.

[10] 贾瑞生,赵同彬,孙红梅,等.基于经验模态分解及独立成分分析的微震信号降噪方法[J].地球物理学报,2015,58(3):1013-1023.

[11] 李立峰.基于独立分量分析的快速定点算法[J].无线电通信技术,2003,29(6):44-46.

[12] 耿永强,危韧勇. 基于ICA和SVM的滚动轴承故障诊断方法研究[J]. 电子技术应用,2007,33(10):84-86.

[13] 肖盛燮,吕恩琳.离散型区间概率随机变量和模糊概率随机变量的数学期望[J].应用数学和力学,2006,26(10):1253-1260.

[14] 张军龙,刘立程,俞坤游. 基于NSCT的独立分量分析方法[J]. 微型机与应用,2013,32(20):44-47.

[15] 王沙,杨志安,任中京.动态光散射检测电机转速的互信息函数分析[J].光学技术,2005,31(5):758-760.

[16] 石嘉川.基于模糊评价的配电网络多目标优化研究[D].济南：山东大学,2007.

[17] BURCH R, CHANG G, GRADY M, et al. Test systems for harmonics modeling and simulation[J]. IEEE Transactions on Power Delivery, 1999,14(2): 579-587.

[18] TENG J H, CHANG C Y. Backward/forward sweep-based harmonic analysis method for distribution systems[J]. IEEE Transactions on Power Delivery, 2007, 22(3):1665-1672.

[19] TENG J H. A network-topology-based three-phase load flow for distribution systems[C]. Proceedings of National Science Council Republic of China Part a Physical Science and Engineening, 2000,24: 259-264.

[20] GURSOY E, NIEBUR D. Impact of sample size on ICA-based harmonic source estimation[C]. Proceedings of the 13th International Conference on Intelligent Systems Application to Power Systems, 2005,11(1): 123-127.

2017-03-31)

张翠(1993-)，通信作者，女，硕士研究生，主要研究方向：电力系统及其自动化控制。E-mail：1398244816@qq.com。

党幼云(1962-)，女，学士，教授，主要研究方向：电力电子电源技术与运动控制系统。

罗辉(1991-)，男，硕士研究生，主要研究方向：电力系统及其自动化控制。

A new method for determining multiple harmonic source locations in a power distribution system

Zhang Cui, Dang Youyun, Luo Hui, Dong Tan, Li Jingxuan

(School of Electronic and Information, Xi’an Polytechnic University, Xi’an 710048, China)

Based on the independent component analysis and mutual information theory, the paper researches the locations of multiple harmonic sources in the distributed system.The independent component analysis is used to estimate the distribution of the injected harmonic current caused by the harmonic source. The mutual information theory is used to verify the accuracy of this method, and the simulations of IEEE 34 bus, IEEE 30 bus and IEEE 33 radial distribution system are carried out. The results show that the method can accurately estimate the location of multiple harmonic sources without knowing the network parameters in advance, and provide the basis for harmonization of harmonic control and effective separation of harmonic liability.

multiple harmonic source locations; independent component analysis; mutual information theory

TM726.2

A

10.19358/j.issn.1674- 7720.2017.22.023

张翠，党幼云，罗辉，等.一种用于确定配电系统中多个谐波源位置的新方法J.微型机与应用，2017,36(22)：87-90.