数列极限与函数极限的统一
唐海波
(汉江师范学院 教育系,湖北 十堰 442000)
数列极限与函数极限的统一
唐海波
(汉江师范学院教育系,湖北十堰442000)
极限思想是高等数学中常用的思想方法,也是解决函数问题最基本和最常用的方法。函数极限表现为自变量在变化过程中函数值的变化趋势;数列作为一种特殊的函数,可以用函数性质及其相关思想方法对数列进行学习和研究;数列极限与函数极限之间存在较多相似之处,但同时也有很多不同之处,研究数列极限与函数极限之间的异同点,就应当把握“数列是特殊的函数”这一关键点。从数列极限与函数极限的定义和性质出发,介绍二者之间的异同点,并从极限的定义、极限的证明、极限的求解方法等方面描述二者之间的统一。
极限;数列;函数;统一
0 引言
极限是高等数学中极为重要的内容板块,同时极限思想也是进行数学分析的主要方法[1]。在高等数学中,有较多的内容体系,诸如连续、导数及积分等都与极限密切相关,都可以通过极限进行定义和描述。因而,从极限的定义与性质出发,掌握丰富的极限理论,熟练运用极限思想和方法,这在数学分析及解决数学问题方面至关重要。数列是特殊的函数,其定义域为自然数集,可以用函数的性质及相关的思想方法对其进行研究[2]。数列极限与函数极限之间存在较多的联系,二者既有区别,也相互统一,本文从数列极限与函数极限的定义与性质出发,介绍二者之间的异同点,并从极限的定义、极限的证明、极限的求解方法等方面解析二者之间的统一与联系。
1 数列极限
1.1 数列极限的定义
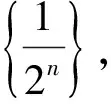
即当n趋于无穷大时,数列an将无限趋近于A或数列an的极限为A。若数列的极限存在,则称此数列属于收敛数列,若不存在则表示数列发散。
上述数列定义所对应的几何意义如下:以A为中心,以ε为半径所对应的任意一个开区间(A-ε,A+ε),都能够于数列{an}中找出某一项aN,使aN之后的任意项均处于这一开区间中,并且在此区间以外,最多存在数列{an}中的有限项。
上述定义中的正整数N应当关注以下两点:①N是基于ε存在的,通常情况下,N是随着ε值的减小而不断增大的,但正整数N并不唯一;②在上述定义中仅仅是注重正整数N的存在性,而不是找出其中最小的正整数N,我们仅仅关注第N项之后的各项均可以保持与常数a之间的距离小于给定的任意小正数ε。
1.2 数列极限的性质
一数列{an}具有极限,说明此数列收敛,其具有以下几方面性质:
(1)如果数列极限存在,则此极限必定是唯一的;
(2)如果数列{an}是收敛的,则{an}必定是有界数列;
(3)如果数列{an}存在极限,且为A,则数列{an}的任何一个子数列{ank}也必定收敛于A;
(4)保号性,如果数列极限A为正数,则一定存在正整数N1,当ngt;N1时有angt;0;
定理1:(收敛数列及其对应奇、偶项数列之间的关系)数列{an}能够收敛于a一个充要条件为{an}的奇数项数列{a2k-1}以及偶数项数列{a2k}均收敛,且都收敛于a。
2 函数极限
2.1 函数极限的定义
(1)当自变量为有限值时对应的函数极限
函数f(x)在某点x0相应去心邻域,即U0(X0)中有定义,若对于任何既定的正数ε,且不管其值如何小,总会存在一正数δ,保证不等式0lt;|X-X0|lt;δ所规定所有自变量x,相应函数值f(x)均符合不等式|f(x)-A|lt;ε,此时称常数A是函数f(x)基于x→x0时所对应的极限,并记作
函数极限定义的几何意义如下:将上述函数极限的定义用几何语言进行描述:①对于任意正数ε,并以两条直线y=A+ε与y=A-ε作为边界所形成的区域;②总会有δgt;0,并以点x0为中心,以δ为半径所构成的圆域;③当x满足不等式0lt;|x-x0|lt;δ时,即x位于上述圆域中;④总会有|f(x)-A|lt;ε成立,即函数f(x)所对应的图像是位于这一带形区域中的。
(2)当自变量为无穷大时相应函数所对应的极限
函数f(x)自变量满足|x|gt;0,若任意给定εgt;0,必会存在某一正数Χ,对于满足不等式|x|gt;Χ所对应的所有自变量x,相应函数值f(x)均满足|f(x)-A|lt;ε,此时将常数A称为函数f(x)当自变量x→∞时所对应的极限,并记作
且y=A是函数y=f(x)对应图像的水平的渐近线。
2.2 函数极限的性质





定理2:对于函数f(x)在x→x0时,其极限存在的一个充要条件为函数f(x)在x→x0时所对应的左、右极限均存在,且相等,即

3 数列极限与函数极限之间的异同
(1)如果极限存在那么极限值一定是唯一的,因而数列极限及函数极限均具有唯一性。
(2)若数列极限是存在的,则其是有界的,并且数列的整体是有界的,也就是存在正整数M,对于对数列中的所有项均有|an|≤M,但函数界性与此不同,函数极限表现为一种局部性,例如当x趋近于正无穷时,函数极限相应局部有界性可以表述为:存在正数M,保证f(x)在自变量xgt;M的区域中满足|f(x)|≤M,在这里主要注重局部性,并不考虑比M小于函数值其是否有界,因而,函数极限所表现的局部性是与数列极限存在本质区别的。
(3)数列极限是否存在的判别方法主要有两个,即单调有界定理及柯西收敛准则,这是高等数学中对于数列极限进行判断的常用方法[3]。基于单调有界定理,若一个数列是单调递增的,且有上界,此时便可以判定数列极限是存在的,并且其极限值就是数列对应的上确界,同理,若一个数列是单调递减的,并且具有下界,此时也可以说此数列极限是存在的,并且极限值为其下确界。
基于柯西收敛准则,随着n值的增加,收敛数列其各项值将会越来越靠近,因而当n值适当时,必然会有任意两项的距离能够小于所给定的任何一个正数ε。柯西收敛准则可以根据数列自身的特点进行极限存在与否的判定。与函数极限相应存在条件相比,数列极限中的柯西准则是与函数极限完全类似的,而所不同的就是在函数极限中涉及了归结原则,也就是海涅定理。然而,在实际的运用中,基于柯西收敛准则进行极限的判断是不太现实的,对于数列来说,收敛于x0的数列有很多,因而,我们不可能针对每一个数列都去验证其极限值。在实际的解题过程中,运用的最多的就是其推论:通过找到一个数列,其收敛于x0,但函数的极限值并不存在,或者找到同时收敛于x0的两个数列,然而这两个函数的极限值并不相等。上述推论与通过寻找数列的子列来判断数列极限存在与否的方法是一致的,这两种方法的思路也是完全一样的。对于函数极限来说,单调有界定理同样适用,但该定理用在函数的表达中因为其单调具有增减的变化,因而只能对函数一侧进行研究,也就是只能对单侧极限进行研究。其方法与数列极限有较大的相似之处,只需要进行适当的调整即可。
(4)数列极限与函数极限在其应用方面也存在较多的相似之处,诸如极限的四则运算及相应的证明过程,而对于平均收敛及几何收敛方面也存在一定的相似之处,只需要进行稍微改动就可以互通使用。但这里应当注意一点,在运用洛必达法则时,若对数列极限进行处理,应当先将数列极限转化为函数极限,然后借助归结原则求解数列极限,这主要是因为洛必达法则不能直接用于求解数列极限,其原因在于对离散变量取导数并没有实际意义。
4 数列极限与函数极限之间的统一
4.1 数列极限与函数极限在定义上的统一
数列及函数极限都可以通过定义来进行证明,即借助ε-δ(或N)描述进行证明,一般步骤如下:
若极限为有限值时,相应证明过程如下:
(1)首先给定任意一个正数ε;
(2)求解不等式|f(x)-A|lt;ε或|an-A|lt;ε,找出δ或N值;
(3)选定δ或N值;
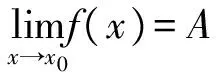
若极限值为无穷大,相应证明过程如下:
(1)给定任意一个正数G;
(2)求解不等式f(x)gt;G(或f(x)lt;-G);
(3)选定δ值;

4.2 数列极限与函数极限在极限的存在条件方面的统一
(1)夹逼定理
①数列极限中的夹逼准则
若数列{an},{bn}与{cn}均满足以下条件:(i)存在正整数N,当ngt;N时,有bn≤an≤cn;(ii)数列{bn}与{cn}的极限相等,且为a,此时数列{an}极限一定存在,且为a[4]。
②函数极限的夹逼准则

(2)柯西准则
①数列极限的柯西准则
数列{an}收敛的充要条件为:对于任意给定的正数ε,存在正整数N,使得当m,ngt;N时,有|xn-xm|lt;ε成立。
②函数极限的柯西准则
设函数f定义域为x0的去心邻域U0(x0;δ′),那么f(x)当x→x0极限存在的一个充要条件为:对于任意给定的正数ε,一定有正数δlt;δ′,保证对任意x′,x″∈U0(x0;δ′)时,有|f(x′)-f(x″)|lt;ε成立[5]。
(3)归结原则(海涅定理)

对于归结原则的理解和运用应当关注以下两个方面:
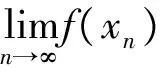
归结原则能够将函数极限和数列极限相应存在性紧密地联系在一起,基于归结原则我们能够对两种极限之间的区别与联系进行清晰而准确的理解和认识。归结原则其另一个重要作用和意义在于能够将函数极限转化为数列极限或是将数列极限转化为函数极限来进行处理,这体现了数列极限与函数极限之间的统一性。
4.3 数列极限与函数极限求解方法上的统一
尽管数列极限和函数极限的定义是相互独立的,但两者之间存在较为明确的联系。下面通过归结原则在数列极限与函数极限中的运用来描述两者在求解方面中的联系与统一[7]。
(1)用数列极限来求解函数极限



运用归结原则实现函数极限与数列极限之间的转化,应当注意以下两点:
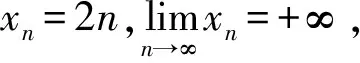
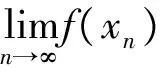
(2)用函数极限求解数列极限
运用函数极限来求解数列极限,要求实现数列极限向函数极限的转化。目前,求解函数极限的方法很多,如可以运用函数对应的连续性特征,借助洛必达法则,将函数以泰勒公式展开,或者运用变量代换等相应方法。对于数列向函数的转化主要是借助归结原则[8]。
运用函数一系列基本性质,我们可以将数列施以必要的恒等变形,将其转化为函数形式,然后再借助函数极限相应性质、求解思想以及归结原则,对转化后的函数极限进行求解。
例如:


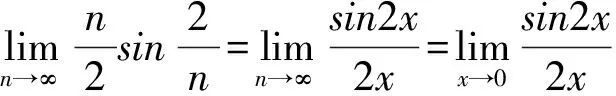
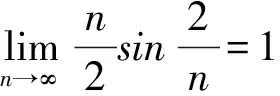
解:首先将此数列极限进行转化,即
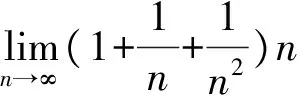
对函数取对数有:

4.4 数列极限与函数极限在应用上的统一
数列极限与函数极限在应用方面存在较多的相似之处,诸如四则运算及相应证明过程,平均收敛与几何收敛、证明过程以及一些构造性的方法等,二者的基本思路大致相似,仅需要依据条件进行稍微改动就可以了。然而这里应强调一下,在运用洛必达法则时,若遇到数列极限的处理时,应首先转化为函数极限,然后在进行求解,最后运用归结原则求出数列的极限值,这是因为在数列极限的形式下是无法运用洛必达法则的,主要是离散变量的求导其本身没有意义,因而这一点应当特别注意。
5 结语
数列作为特殊的函数,其定义域是自然数集,定义域上的特殊性使得数列极限较为简单,具有一系列较为特殊的性质,并且这些性质体现出较为明显的特殊性;而对于函数其定义域为实数集,因而其极限表现出较为明显的局部性。数列极限与函数极限之间存在较多差别,同时也紧密联系,因而在极限的求解与运用过程中要能够明确二者之间的区别与联系,善于将数列极限与函数极限统一起来,综合运用极限求解思想和方法来解决实际问题。
[1]张德华.浅析高中数学中有关极限的知识[J].考试周刊,2012(37):66-67.
[2]游志林.浅析数列极限与函数极限的异同——以华东师范大学《数学分析》第四版为例[J].文理导航,2017(11):35-35.
[3]何天荣.数列极限与函数极限的异同及其本质原因[J].考试周刊,2016(55):58-58.
[4]贺飞,刘德.用数列极限计算函数极限的夹逼定理[J].高等数学研究,2007,10(5):5-8.
[5]蒋志强.函数极限的几种特殊求法[J].牡丹江教育学院学报,2009(5):122-123.
[6]张梦阳.一类用数列极限计算函数极限的方法[J].成才之路,2012(33):33-33.
[7]王金芝.数列极限与函数极限的统一[J].科技致富向导,2010(26):74-75.
[8]曾祥远,程功任,李科赞.关于函数和数列极限的相关理论及计算方法的探讨[J].教育现代化,2015(12):253-256.
2017-09-23
[责任编辑姚胜勋]
TheUnificationoftheSequenceLimitandFunctionalLimit
TANGHaibo
(DepartmentofEducation,HanjiangNormalUniversity,ShiyanHubei442000,China)
Limit thought is a common thought method in higher mathematics,which is also the most basic and commonly used method in solving function problems and research.The function limit shows the change of function value in the change process of the independent variable.As a special function,the sequence can be learned and studied by the function and its related thought methods.Sequence limit and function limit have many similarities,but also a lot of differences.The study of similarities and differences between the sequence limit and function limit should grasp the "the sequence is a special function" as the key point.This article,from the definition and nature of sequence limit and the function limit,introduces the similarities and differences between them,and from the definition of limit,the proof of limit,limit’s solving method,describes the unification of them.
limit;the sequence;functions;unification
O143
A
1672-9021(2017)05-00070-06
唐海波(1980-),男,湖北丹江口人,汉江师范学院教育系讲师,主要研究方向:高等数学,初等数学。

