Fredholm算子指标在紧扰动、小扰动下的不变性

陈永翠

(重庆师范大学 数学科学学院，重庆 401331)

Fredholm算子指标在紧扰动、小扰动下的不变性

陈永翠

(重庆师范大学 数学科学学院，重庆 401331)

主要研究了Fredholm算子及其指标分别在紧扰动和小扰动下的变化情况;验证了抽象指标与传统指标本质相同;并利用开集、同态映射和Fredholm算子的性质对Fredholm算子及其指标分别在紧扰动和小扰动下的不变性给出了相应的证明.

紧算子；Fredholm算子；紧扰动；小扰动；不变性

本文在介绍了紧算子的前提下给出了Fredholm算子[1]定义及Fredholm算子的相关性质,做出了Fredholm算子在小扰动下不变的又一种证明,该方法单纯使用开集及连续映射进行论证,较文献[2]中利用Fredholm算子性质证明的方法更简洁,更易理解.此外，本文另一个工作是建立起了抽象指标与传统指标间的等价性关系,并利用开集、同态映射以及Fredholm算子的相关性质,证明了Fredholm算子的指标在小扰动、紧扰动下的不变性.其实,Fredholm算子及其性质在数学的很多分支中都有着极其广泛的应用,多用于研究例如Hilbert空间、Dirichlet空间、Fock空间[3]等空间中各种算子的一些性质[4-8],此外，人们还进一步考察了半Fredholm算子及其指标等相关问题[9].可见,Fredholm算子在数学研究中也占据着不容忽视的地位.

1 预备知识

定义1 若H是一个无限维Hilbert空间,算子T∈L(H),称T是一个有限秩算子,若dimranTlt;∞.H上有限秩算子全体记为LF(H).称T是一个紧算子[10],若T将H中单位球映为列紧集，即T(H)1的闭包是紧集.H上紧算子全体记为LC(H).

注：本文中讨论的都是H为无限维Hilbert空间的情形,因为当H是有限维Hilbert空间时L(H)= LC(H).

定义2 若H是Hilbert空间，则商代数L(H)∕LC(H)是Banach代数[11-12],称为Calkin代数.

下面验证L(H)∕LC(H)是Banach代数线性空间.

证明要证L(H)∕LC(H)是Banach代数,首先需证L(H)∕LC(H)是代数：

自然同态Π：L(H)→L(H)∕LC(H),

对任意Π(T),Π(S)∈L(H)∕LC(H),因为Π同态,所以对任意λ∈R或C,T,S∈L(H),

Π(λT)=λΠ(T),Π(TS)=Π(T)Π(S)

对任意α,β∈R或C,Π(T),Π(S),Π(R)∈L(H)∕LC(H)

Π(T)={Π(T+K1)| T∈L(H),K1∈LC(H)}，Π(S)={Π(S+K2)| S∈L(H),K2∈LC(H)}

α{Π(T+K1)| T∈L(H),K1∈LC(H)}+β{Π(S+K2)| S∈L(H),K2∈LC(H)}=

αΠ(T)+βΠ(S)=Π(αT+βS)={Π(αT+βS+K |αT+βS∈L(H),K∈LC(H)}

所以,αΠ(T)+βΠ(S) ∈L(H)∕LC(H),其他几条性质容易验证.

因此,L(H)∕LC(H)是线性空间.再证L(H)∕LC(H)是代数：

Π(TSR)=Π(TS)Π(R) =Π(T)Π(S)Π(R)=Π(T)(Π(S)Π(R))=Π(T)Π(SR)

所以,结合律成立.

注：T∈L(H)，S∈LC(H),TS∈LC(H)

(Π(S)+Π(R))Π(T)= Π(S+R)Π(T)=Π((S+R)T)=Π(ST+RT)=Π(ST)+Π(RT)=

Π(S)Π(T)+Π(R)Π(T)

Π(T)(Π(S)+Π(R))= Π(T)Π(S+R)=Π(T(S+R))=Π(TS+TR)=Π(TS)+Π(TR)=

Π(T)Π(S)+Π(T)Π(R)

所以,左右分配律成立.

α(Π(T)Π(S))= α(Π(TS)) =Π(αTS)=Π((αT)S)=Π(αT)Π(S)=(αΠ(T))Π(S)=

Π(T)(αΠ(S))

综上所述,L(H)∕LC(H)是一个代数.

L(H)∕LC(H)={ [Π(T)]| Π(S)∈[Π(T)],T+ K=S,K∈LC(H)}

L(H)∕LC(H)上范数定义为：

‖[Π(T)]‖=inf{‖Π(R)‖：Π(S)∈[Π(T)]}≤‖Π(T)‖

‖[Π(T)][Π(S)]‖ =inf{‖Π(Q) Π(W)‖：Π(Q)∈[Π(T)],Π(W)∈Π(S)}≤

‖Π(T)‖‖Π(S)‖

所以,L(H)∕LC(H)是一个赋范代数.最后证明L(H)∕LC(H)完备,显然.

所以,L(H)∕LC(H)是Banach代数.

不难验证Calkin代数实质上是一个C*代数.

证明：设H是Hilbert空间，对任意T,S∈L(H),α,β∈R或C,有：

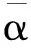
④(ST)*=T*S*;⑤‖T‖2=‖T*T‖;

不妨设对合映射*：L(H)∕LC(H)→L(H)∕LC(H)，Π(T) →Π(T)*

因为L(H)∕LC(H)是一个Banach代数,所以对任意的Π(T)∈L(H)∕LC(H),存在唯一的表示

Π(T)= Π(U)+ iΠ(V)[11],其中Π(U), Π(V)是自伴算子.所以只需考虑L(H)∕LC(H)中自伴元即可.

若T为自伴元，则Π(T)=Π(T*)

又因为Π(T)={T+K|K∈LC(H)}，又有对任意K∈LC(H),则K*∈LC(H)

所以Π(T)*={T+K|K∈LC(H)}*=Π((T+K)*)=Π(T+K*)=Π(T)=Π(T*)

下面验证Calkin代数是一个C*代数.对任意T,S∈L(H),α,β∈R或C

(i) Π(T)**=((Π(T)*)*=Π(T*)*=Π(T**)=Π(T);

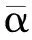
(iii) ( Π(T)Π(S))*=(Π(TS))*=Π((TS)*)=Π(S*T*)=Π(S*)Π(T*)=Π(S)*Π(T)*

(iv) 因为‖Π(T*)‖=inf{‖Π(S*)‖∣S～T }=inf{‖Π(S)‖∣S～T}=‖Π(T)‖

所以,‖Π(T)*Π(T)‖ =‖Π(T*)Π(T)‖=‖Π(T*T)‖=‖Π(T)‖2

故Calkin代数是一个C*代数.

定义3 设H是Hilbert空间,自然同态Π：L(H)→L(H)∕LC(H),T∈L(H).若Π(T)是L(H)∕LC(H)中的可逆元,则称T是一个Fredholm算子,H上Fredholm[11，13]算子全体记为F(H).

定义4 若H是Hilbert空间，则传统指标函数j：F(H)→.使得j(T)=dim kerT-dim kerT*,对n∈,集合Fn={T∈F(H):j(T)=n}.

定理1 若H是Hilbert空间,则F(H)是L(H)的一个开子集,且F(H)自伴,乘法封闭,在紧扰动和小扰动下都保持不变[2,12].

定理2[12]若H是Hilbert空间,T∈F0且K∈LC(H),则T+K∈F0.

2 结论及其证明

在前面已有F0在紧扰动不变的情况下进一步讨论Fn在紧扰动下的变化情况.要证明Fn在紧扰动下的变化情况,直接证明不太好入手,现不妨定义抽象指标i如下：

定义5i：F(H)→ΛL(H)/LC(H),使得i=γοП,其中γ是对Banach代数L(H)/LC(H)的抽象指标.即i：F(H)→L(H)/LC(H)→ΛL(H)/LC(H).

现验证i连续,可乘.

证明：先证i连续,因为Π是一个同态且F(H)是开集,所以G={Π(T)|Π(T)-1存在}是L(H)/LC(H)中的开集,所以,F(H)=Π-1(G),由此可得Π连续.又因为Λ离散,所以i连续.再证i可乘,对任意T,S∈F(H),TS∈F(H),有：i(TS)=γοП(TS)=γο(Π(T)Π(S))=(γοΠ(T))(γοΠ(S))=i(T)i(S).

所以i可乘.

若能证得指标i与j等价,则可用i验证j的性质.现证i,j本质上是一致的.

定理3 传统指标j与抽象指标i实质相同.

证明：假设存在映射α∶Z→ΛL(H)/LC(H),使得下表交换：

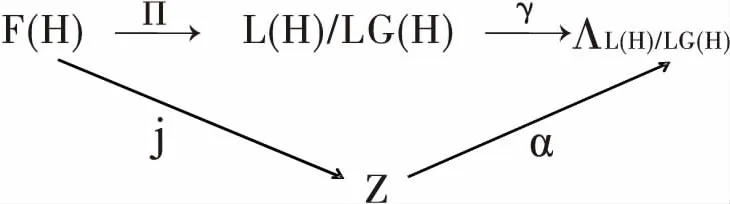
对每个n,集合Fn=j-1(n)={T∈F(H)∶j(T)=n}连通[14].

可知,α良定义：因为i连续,Λ离散,所以i作用在F(H)上一定为常量.所以α(n)=i(T)良定义且α一定连续.再证α是同构,只需证α同态且一一映射.先验证α同态：

i(T)=γοΠ(T)=αоj(T)=α(n)，i(Tk)=ki(T) =kα(n)，其中k∈+

所以,若j(T)=n,j(S)=m,则有

i(TS)=γο(Π(TS)=γο(Π(T)Π(S))=(γοΠ(T))( γοΠ(S))=α(j(TS))=α(j(T)+j(S))=α(n+m)

又因为i(TS)=i(T)+i(S)=α(n)+α(m)

所以,α(n+m)= α(n)+α(m)

即i可乘性成立.

λ个

所以线性性成立.因此,α是一个同态.

最后证明α是一一映射.因为i是满射,所以α为满射.验证单射：因为对任意T∈F(H),K∈LC(H),有Π(T+K)=Π(T).所以,i(T+K)=i(T),即i在紧扰动下不变.进而有keri= F0,所以α是单射，从而是一一映射.

由上可得α是同构映射,所以指标i与j本质上是相同的且j在紧扰动下不变,j连续、可乘.

定理4 对任意T∈F(H),K∈LC(H),有j(T+K)=j(T).

定理5 对任意T∈F(H),S∈L(H),存在δgt;0,当‖S‖lt;δ时，有j(T+S)=j(T).

证明：在前面定义5中证明i连续时已经知道

(*1)对任意开集G∈L(H)/LC(H)，G={Π(T)|Π(T)-1存在}是开集，所以Π-1(G)存在且是开集.因此对任意T∈F(H),存在δgt;0,使得U(T,δ)⊂F(H),对任意F∈U(T,δ),有‖F-T‖lt;δ.不妨令F-T=S,‖S‖lt;δ,从而有：‖T+S-T‖=‖S‖lt;δ. 所以T+S∈U(T,δ), T+S∈F(H).(*2)又因为i连续,所以对任意εgt;0,∃δgt;0,使得：当‖F-T‖lt;δ时,令S=F-T,‖S‖lt;δ有：

∣i(F)-i(T)∣lt;ε,即∣i(T+S)-i(T)∣lt;ε

所以i在小扰动下不变,得证.

注：上述证明中(*1)～(*2)的内容可作为定理1中F(H)小扰动下不变性的另一证明方式.

[1] 葛晓葵.Fredholm算子的一个注记[J].广东第二师范学院学报，2000，20(3)：28-30.

[2] 张恭庆,林源渠.泛函分析讲义上册[M].北京：北京大学出版社，2015:246-247.

[3] 叶鹏,于涛,吴时月.Fock空间上对偶Toeplitz算子的紧性[J].温州大学学报，2008,29(2)：26-31.

[4] 卢玉峰.Toeplitz算子的Fredholm性质[J].东北师大学报学报.1996(3):21-23.

[5] 郭坤宇.强拟凸域上Toeplitz算子的Fredholm指标公式及相关问题[J].数学年刊，1996,17A(3):347-352.

[6] 夏锦,王晓峰,曹广福.调和Dirichlet空间D1h上有界、紧与Fredholm的Toeplitz算子[J].数学物理学报，2015,35A(5):956-969.

[7] 俞威新.序群上FredholmToeplitz算子的特征[J].嘉兴学院学报，2010,22(3):14-16.

[8] 夏锦，胡坤. 加权Dirichlet空间D上Toeplitz算子的紧性与Fredholm性质[J].广州大学学报. 2015， 14(6):1-8.

[9] 李亚亚,王昌.紧算子理论成因探析[J].自然辩证法研究. 2014，30(12)：80-84.

[10] 赵玲玲,任晴晴,靳志同.一致Fredholm指标性质与(ω)性质判定[J].系统科学与数学. 2014，34(3):376-384.

[11] 马吉溥.Hilbert空间子空间的维数和半Fredholm算子的指标[J].中国科学(A辑)，1996(9)：783-792.

[12] RONALD G，DOUGLAS.Banach Algebra Techniquesin Operator Theroy[M].Second Edition.Springer-Verlag，2012:113-121.

[13] 郭坤宇.算子理论基础[M].上海：复旦大学出版社，2014:75-83.

[14] WALTER RUDIN.Functional Analysis[M].Second Edition.Newyork:MeGraw Hill，1991:286.

责任编辑：時凌

TheInvariantoftheIndexoftheFredholmOperatorUnderCompactPerturbationamp;SmallPerturbation

CHEN Yongcui

(School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,China)

In this article,we studied the changes of Fredholm operators and its index under compact perturbation amp; small perturbation.We also proved that the classical indexiand the abstract indexjare essentially the same.At last,we gave the proofs of invariation by the properties of open set,homomorphic mapping and Fredholm operators.

compact operator;Fredholm operator;compact perturbation;small perturbation;invariation

2016-11-25.

重庆市研究生科研创新项目(YKC16001)

陈永翠(1994-)，女，硕士生，主要从事泛函分析的研究.

1008-8423(2017)04-0417-03

10.13501/j.cnki.42-1569/n.2017.12.014

O18

A