一类带有执行器故障不确定线性系统的自适应H∞控制

彭晓易，武力兵

（辽宁科技大学 理学院，辽宁 鞍山 114051）

一类带有执行器故障不确定线性系统的自适应H∞控制

彭晓易，武力兵

（辽宁科技大学 理学院，辽宁 鞍山 114051）

针对一类带有不匹配外部扰动、非线性参数不确定性和执行器故障的线性系统，提出一种基于自适应容错技术的H∞控制方案。所设计的变增益容错控制器既可以对外部扰动具有良好的抑制作用，同时也可以有效补偿系统参数不确定和未知故障的影响，进而保证闭环系统具有期望的优化性能指标。飞行控制系统的数值仿真例子表明了所提出控制方法的有效性。

自适应控制；H∞控制；稳定性分析；飞行器模型

一直以来，容错控制是控制理论研究的热点，可以提高系统的安全性，避免不必要的经济损失和人员伤亡［1-5］。同时，伴随容错控制的发展，鲁棒H∞扰动抑制问题［6-9］在控制领域也备受关注，其主要设计思想是抑制线性系统外部扰动到被调输出传递函数的增益，使扰动对闭环系统的影响最小化。H∞控制理论发展近二十年，各方面理论趋于成熟，同时也在导航制导、机械电子、材料化工等领域中得到广泛应用。尽管H∞控制技术可以有效处理外部扰动对闭环系统的影响，但是对于带有执行器故障和非线性参数不确定性线性系统的容错控制问题却无能为力，由此可见这种方法还具有一定的保守性。

近些年来，基于自适应技术的容错控制策略逐渐成为容错控制领域的主流方法，其主要特点是不需要设计故障诊断与隔离机制而直接针对带有未知故障的闭环系统进行在线容错，也进一步避免了因为故障检测阶段的误报或漏报信息导致容错设计失败的情形。文献［10-11］分别基于鲁棒控制模式给出相应的容错控制设计方法；针对一类六自由度机器人模型，文献［12］所提出改进的鲁棒自适应控制算法提高了系统轨迹跟踪估计精度。文献［13］研究了一类一阶不确定非线性时变系统的鲁棒自适应确保跟踪性能控制问题。针对一类不确定非线性故障系统，文献［14］给出了相应的RBF神经网络容错控制方法。文献［15］针对一类带有不确定时延故障的严反馈下三角非线性系统，所设计的自适应神经网络控制器保证了闭环系统实现期望的稳定性能。基于自适应迭代学习和模糊逼近技术，文献［16-17］分别研究了小行星探测器动态模型和不确定时滞关联大系统的容错控制问题。文献［18］考虑了一类带有匹配条件参数不确定性和外部扰动线性系统的容错控制问题，所提出的鲁棒自适应控制算法保证闭环系统的零解是渐近稳定的。应该指出的是，上述文献所提出的控制方法，不能处理带有非线性参数不确定性、不匹配外部扰动和执行器故障线性系统的鲁棒容错控制问题，本文针对这类不确定线性系统，设计了带有参数更新律的自适应H∞容错控制器，可以有效处理故障并保证了闭环系统具有期望的优化性能指标。

1 问题描述

考虑如下一类不确定线性系统

式中：x(t)∈Rn为系统状态；z(t)∈Rp为系统的被调输出；ω为外部干扰输入；f(x,t)为非线性向量函数，且满足下面的匹配条件

其中g(x,t)为合适的非线性向量函数。执行器漂移故障模型

其中：F(t)为时变故障向量；u(t)为实际的控制输入信号。此外，A,B,C和Bω是已知的具有适当维数的常数矩阵。

自适应控制器采用如下形式

将式（2）、（3）和（4）带入到式（1）中，可以得到如下的闭环系统

本文的控制目标是要设计基于状态反馈模式的自适应 H∞控制器（4），使得线性系统（1）在带有非线性参数不确定性、外部扰动和执行器故障的情况下，闭环控制系统（5）在ω=0时渐近稳定；当ω≠0时，系统增益Γee不超过性能指标γ0。

2 容错控制设计与定性分析

2.1 直接自适应控制器设计

给出自适应控制器（4）中变增益项KA的表达式

其中σ(t)∈R+是一致连续函数并且满足

其中 σˉ是正常数，初始时刻 t0≥0 ，k1,k2是 k1,k2的在线估计值，自适应律满足

式中 γ1,γ2是正的设计参数，进一步记-k*i,i=1,2，则可以得到下面的动态误差系统

为了设计容错控制方案，做出如下假设和引理：

假设1 {A,B}是可稳定的，并且系统所有状态都是可测的。

假设2 F(t)和g(x,t)都是连续的有界函数，即存在一个未知上界使得

2.2 稳定性分析

定理1 考虑闭环控制系统（5），采用自适应控制器（6）和以及自适应控制律（8），如果存在矩阵K和正定矩阵P满足下述不等式

则当ω=0时闭环系统（5）是渐近稳定的；当ω≠0时，系统增益Γee不超过性能指标γ0。

证明 取Lyapunov函数

沿系统（5）对其求导得

由假设2可得

进一步，根据引理1，对任意的正常数η，下面的不等式成立

将控制器（6）和动态误差系统（9）带入式（14）得到

通过以上的讨论可知当ω=0时，系统是趋于渐近稳定的；当ω≠0时，系统增益小于性能指标，即Γee＜γ0。 证毕。

3 仿真算例

为了表明本文所提出的自适应H∞容错控制方法的有效性，采用波音747飞行控制系统的线性化模型作为仿真算例［21］，状态空间方程如下

式中：x=[β,yr,p,φ]T，其中 β 表示侧滑角，yr表示偏航率，p表示滚转率，φ表示滚转角；u(t)=[δr1,δr2,δr3]T是表示三个方向舵的伺服控制系统。系统参数矩阵

此外，故障和非线性参数不确定性选为F=[-2 0-0.8]T,g(x,t)=0.1sin(πt)。进一步，通过Matlab解矩阵不等式（17）得

在仿真中，控制器参数选取为σ(t)=10e-2t,η=10,γ1=γ2=30,γ0=2 。初始条件满足 x(0)=[0.5,-0.8,-1,0.8]T,k1(0)=2,k2(0)=2 ，则在 Simulink 环境下仿真得到图1～图3。

在仿真时，假设飞机在飞行过程的前14 s内受到气流等因素对系统的扰动为ω=0.5cos(t)，此时系统增益小于性能指标，即 Γee＜γ0。14 s后ω=0，从图1中可以看出闭环系统状态曲线是渐近稳定的。图2～图3分别是自适应估计曲线和控制输入信号，可以看出所有闭环信号都是有界的。

图1 系统状态响应曲线Fig.1 Respond curves of system states

图2 自适应律ki(i=1,2)响应曲线Fig.2 Respond curves of adaptive lawski(i=1,2)

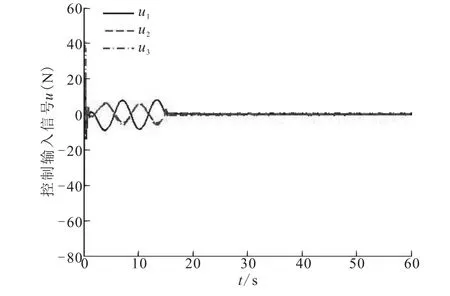
图3 控制信号ui(i=1,2,3)响应曲线Fig.3 Respond curves of control signalsui(i=1,2,3)

4 结论

本文针对一类带有执行器故障的不确定线性系统，设计了自适应H∞控制器和相应的参数更新律，并给出了此类系统容错控制器存在的充分条件。所设计的自适应控制算法能够保证闭环系统在带有非线性向量函数，外部扰动以及执行器故障情况下具有期望的优化性能指标。数值仿真例子说明了所提出方法的有效性。

［1］YANG G H，WANG J L，Soh Y C.ReliableH∞controller design for linear systems［J］.Automatica，2001，37（5）：717-725.

［2］王福利，张颖伟.容错控制［M］.沈阳：东北大学出版社，2003：2-5.

［3］王仲生.智能故障诊断与容错控制［M］.西安：西北工业大学出版社，2005：78-81.

［4］金小铮，杨光红，常小恒，等.容错控制系统鲁棒H∞和自适应补偿控制［J］.自动化学报，2013，39（1）：31-42.

［5］王敏，臧曙，周东华.非线性动态系统的容错控制［J］.计算技术与自动化，2004，23（4）：7-10.

［6］HUA H C，CHUNG M J.MemorylessH∞controller design for linear systems with delayed state and control［J］.Automatica，1995，3（6）：917-919.

［7］YU L，CHU J，SU H Y.Robust memorylessH∞ontroller design for linear time-delay system with nombounded time-varying uncertainty ［J］.Automatica，1996，32（12）：1759-1762.

［8］郑连伟，刘小平，张庆灵.具有时变不确定的线性时滞系统的鲁棒 H∞控制［J］.自动化学报，2001，27（3）：377-380.

［9］伏玉笋，田作华，施颂椒.带非线性摄动的状态延迟系统的 H∞鲁棒控制［J］.自动化学报，2001，27（2）：224-228.

［10］王胜国，谢永成，吕强，等.线性系统的鲁棒容错设计方法［J］.装甲兵工程学院学报，2009，23（4）：57-82.

［11］CHENG X Q，QU J Y，YAN Z P.Robust fault-tolerant controller design for an autonomous underwater vehicle’s navigation control system［J］.Journal of Marine Science and Application，2010，9（1）：87-92.

［12］莫毅.六自由度串联机器人自适应鲁棒控制算法的改进［J］.中国农机化学报，2016，37（5）：232-235.

［13］李公军.一类不确定快时变系统的确保性能鲁棒自适应控制［J］.空间控制技术与应用，2016，42（1）：25-30.

［14］李泽宇，向志军，张士勇.一类不确定非线性系统主动容错控制［J］.辽宁科技大学学报，2015，38（2）：114-118.

［15］徐国平，张显库，张国庆.考虑通信时延的船舶航向保持鲁棒自适应控制［J］.哈尔滨工程大学学报，2017，38（1）：59-65.

［16］黄怡欣，李爽，江秀强.基于自适应迭代学习的小行星绕飞容错控制［J］.中国空间科学技术，2017，37（1）：1-14.

［17］郭涛，陈为胜.不确定时滞关联大系统的全局稳定模糊容错控制［J］.控制理论与应用，2017，34（5）：1-8.

［18］LI X J，YANG G H.Robust adaptive fault tolerant control for uncertain linear system with actuator failures［J］.IET Control Theory and Applications，2012，6（10）：1544-1551.

［19］HUA C C，GUAN X P，SHI P.Adaptive fuzzy control for uncertain interconnected time-delay systems［J］.Fuzzy Sets and Systems，2005，153（3）：447-458.

［20］俞立.鲁棒控制—线性矩阵不等式处理方法［M］.北京：清华大学出版社，2002：8-9.

［21］TAO G，CHENS H，SURESH M J.An adaptive actuator failure compensation controller using output feedback［J］.IEEE Transactions on Automatic Control，2002，47（3）：506-511.

AdaptiveH∞control for a class of uncertain linear systems with actuator failures

PENG Xiaoyi，WU Libing

（School of Sciences，University of Science and Technology Liaoning，Anshan 114051，China）

In this paper，an adaptiveH∞fault-tolerant control scheme for a class of uncertain linear systems with mismatching external disturbances，nonlinear parameter uncertainties，and actuator failures is proposed.By designing the corresponding adaptive controller，the effects of nonlinear parameter uncertainties，actuator failures and external disturbances can be eliminated and restrained simultaneously.Moreover，by using Lyapunov functions method，the designed controller can guarantee the asymptotic stability and the desired performance index of the closed-loop systems.Finally，numerical simulation example of flight control system is provided to show the efficiency of the proposed control method.

adaptive control；H∞control；stability analysis；aircraft model

July 4，2017）

TP273

A

1674-1048（2017）04-0292-06

10.13988/j.ustl.2017.04.010

2017-07-04。

国家自然科学基金项目（61673098）。

彭晓易（1995—），男，天津人。

武力兵（1980—），男，辽宁鞍山人，讲师。